变形Boussinesq方程组的精确解

李　伟，张金良

(河南科技大学 数学与统计学院, 河南 洛阳 471023)



变形Boussinesq方程组的精确解

李伟，张金良

(河南科技大学 数学与统计学院, 河南 洛阳 471023)

摘要：利用简化齐次平衡方法，导出了从一个线性方程的解到变形Boussinesq方程组的解之间的非线性变换。借助于线性方程的解及非线性变换，求出了变形Boussinesq方程组的多重孤波解、有理函数解及关于空间变量的周期解等。

关键词：变形Boussinesq方程组；简化齐次平衡方法；非线性变换；多重孤波解；关于空间变量的周期解；有理函数解

0引言

本文讨论如下形式的变形 Boussinesq方程组:

(1)

其中：u=u(x,t)为水平速度；H=H(x,t)为偏离液体平衡位置的高度。该方程组是一个描述色散波的模型。近年来，齐次平衡方法被广泛用来导出非线性变换、精确解[1-6]以及自贝克隆变换[7-9]。文献[1]用齐次平衡方法得出了变形Boussinesq方程组的单孤波解。简化齐次平衡方法[10]的主要思想是用对数函数A(lnφ)取代原始齐次平衡方法中的待定函数f=f(φ)。本文利用该方法导出了一个线性方程的解到变形Boussinesq方程组的解之间的非线性变换，求出了变形Boussinesq方程组的多重孤波解、有理函数解及关于空间变量的周期解等。这说明利用简化齐次平衡方法求解孤波方程可以得到更丰富的精确解。

1非线性变换

考虑方程组(1)中uux与Hx、(Hu)x与uxxx的齐次平衡 (2m+1=n+1,m+n+1=m+3⟹m=1,n=2)，按照简化齐次平衡方法,可设方程组(1)的解具有下列形式：

(2)

其中：A和B为待定非零常数；φ=φ(x,t)为待定正函数。将式(2)代入方程组(1)的左端可得：

(3)

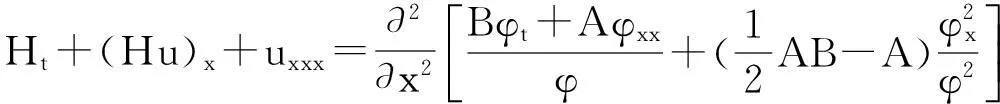
(4)

(5)

解方程组(5)得：

A=±2,B=2。

(6)

将式(6)代入式(2)得：

(7)

利用方程组(5)和式(6),式(3)和式(4)可简化为：

(8)

(9)

只要φ=φ(x,t)满足线性方程：

φt±φxx=0。

(10)

由式(7)~式(10)可得：若函数φ=φ(x,t)是线性方程(10)的一个解，将之代入式(7)，就可得到变形Boussinesq方程组(1)的解；式(7)与线性方程(10)一起构成了由线性方程(10)的解到变形Boussinesq方程组(1)的解之间的非线性变换，从而可借助线性方程(10)的解得到方程组(1)的解。

2变形Boussinesq 方程组的精确解

2.1　变形Boussinesq方程组的多重孤波解

为了解线性方程(10)，假设:

φ=φ(ξ)；ξ=kx+ωt+l,

(11)

其中：k,ω和l为待定常数。

将式(11)代入线性方程(10)得：

ωφ′±k2φ″=0。

(12)

解方程(12)得到如下解：

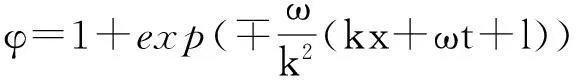
(13)

其中：k,ω和l为任意常数。

将式(13)代入式(7)得：

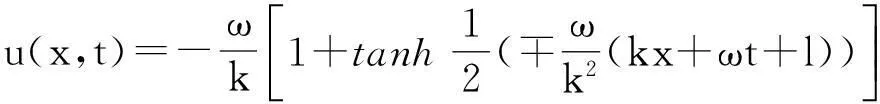
(14)

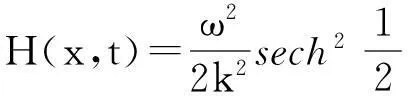
(15)

在文献[1]的式(26)和式(25)中，令c=-ω/k,d=-ω2/k2,e=-ωl/k2,即可分别得到本文式(14)和式(15) (ω/k2的系数取负的情况)。

由于k,ω和l是任意常数，线性方程(10)的解具有线性可加性，可得线性方程(10)的解：

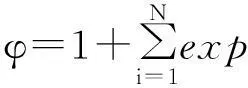
(16)

其中：ki,ωi和li为任意常数，i=1,2,…,N。

将式(16)代入式(7)得：

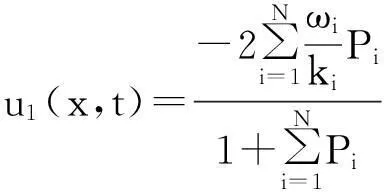
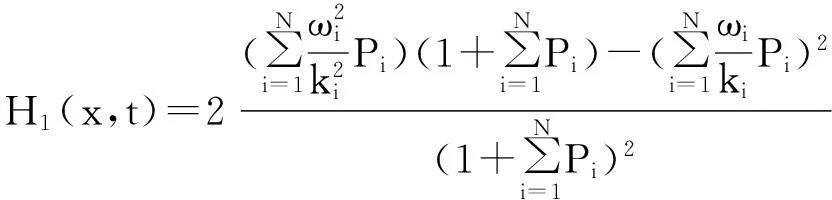
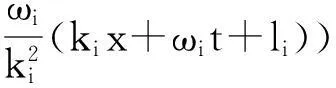
此解是方程组(1)的多重孤波解，在文献[1]中没有出现。

2.2　变形Boussinesq方程组的有理函数解及关于空间变量的周期解

为了得出线性方程(10)的解，假设：

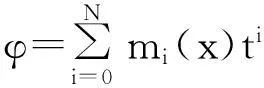
(17)

其中：mi(x)为待定函数，i=0,1,…,N。

将式(17)代入线性方程(10)得：

(m1(x)±m″0(x))+(2m2(x)±m″1(x))t+…+(NmN(x)±m″N-1(x))tN-1±m″N(x)tN=0。

由于上式中1,t,…,tN线性无关,可知它们的系数为0，即:

m1(x)±m″0(x)=0，…，NmN(x)±m″N-1(x)=0； m″N(x)=0。

(18)

解方程组(18)得：

(19)

其中：aj为任意常数。

将式(17)和式(19)代入式(7)，可得方程组(1)的有理函数解：

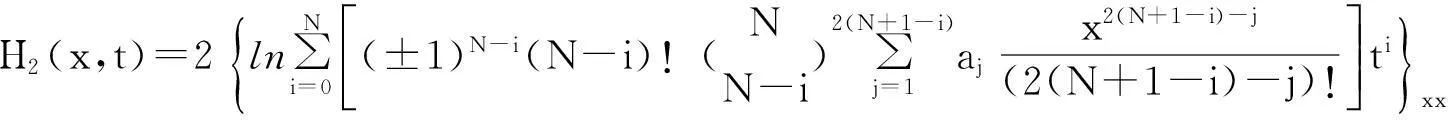
此外，容易得出线性方程(10)有如下解：

(20)

(21)

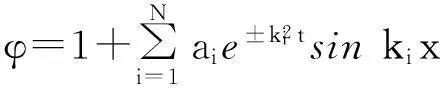
(22)

将式(20)~式(22)分别代入式(7)得到方程组(1)的精确解为：

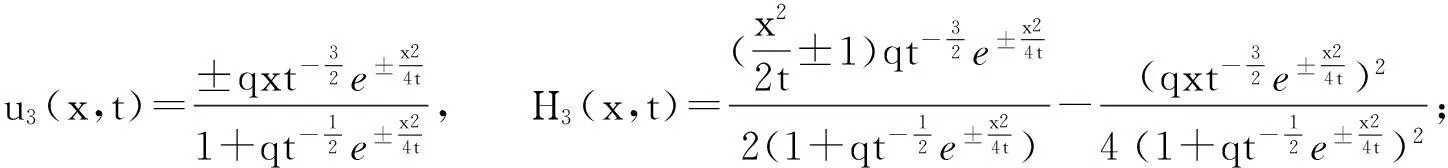
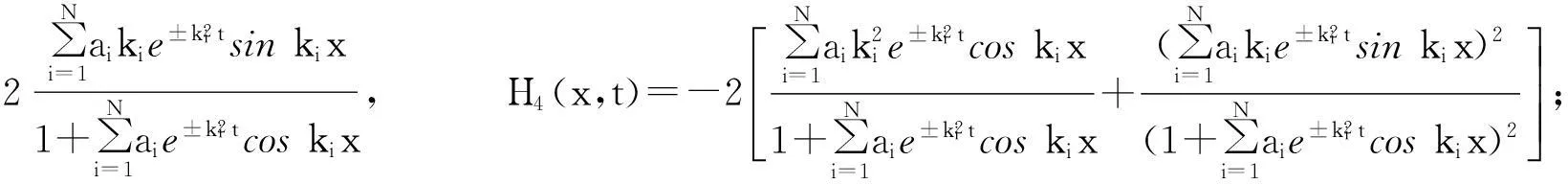
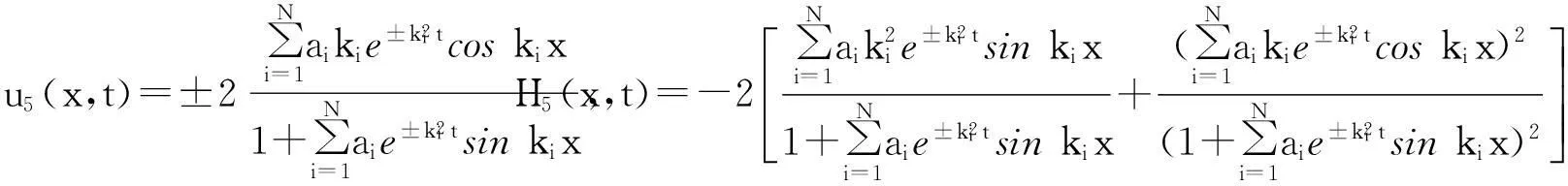
其中：(u4,Η4)和 (u5,Η5)为关于空间变量x的周期解； (u3、Η3)、 (u4,Η4)和 (u5,Η5)在文献[1]中没有出现。

3结论

本文运用简化齐次平衡方法，得到了从一个线性方程的解到变形Boussinesq方程组的解之间的非线性变换。利用该非线性变换，变形Boussinesq方程组被线性化了。利用线性方程组的解，得到了变形Boussinesq方程组的多重孤波解、有理函数解及关于空间变量的周期解。本文所得到绝大部分解在文献[1]中没有出现，表明简化齐次平衡方法是一种更简洁高效的求解非线性发展方程精确解的方法，该方法也可用来求解其他非线性发展方程。

致谢：本文得到王明亮教授的指导，在此表示衷心感谢。

参考文献：

[1]WANG M L.Solitary wave solutions for variant Boussinesq equations[J].Physics letters a,1995,199(3):169-172.

[2]WANG M L.Application of homogeneous balance method to exact solutions of nonlinear equation in mathematical physics[J].Physics letters a,1996,216:67-75.

[3]FAN E G.Two new applications of the homogeneous balance method[J].Physics letters a,2000,265(5):353-357.

[4]EL-WAKIL S A,ABULWAFA E M,ELHANBALY A,et al.The extended homogeneous balance method and its applications for a class of nonlinear evolution equations[J].Chaos,solitons & fractals,2007,33(5):1512-1522.

[5]ZHAO X Q,WANG L,SUN W J.The repeated homogeneous balance method and its applications to nonlinear partial differential equations[J].Chaos, solitons & fractals,2006,28(2):448-453.

[6]李向正,郝祥晖.简化齐次平衡原则与Gerdjikov-Ivanov方程的精确解[J].河南科技大学学报(自然科学版),2015,36(1):82-85.

[7]KHALDALLAH M.Exact traveling wave solutions of the Boussinesq-Burger equation[J]. Mothematical and computer modelling,2009,49(3):666-671.

[8]ABDEL R A S,OSMAN E S, KHALFALLAH M.The homogeneous balance method and its application to the Benjamin-Bona-Mahoney (BBM) equation[J].Applied mathematics and computation,2010,217(4):1385-1390.

[9]王明亮,李志斌,周宇斌.齐次平衡原则及其应用[J].兰州大学学报(自然科学版),1999,35(3):8-16.

[10]WANG M L,LI X Z.Simplified homogeneous balance method and its applications to the Whitham-Broer-Kaup model equations[J].Journal of applied mathematics and physics,2014,2(8):823-827.

文献标志码：A

中图分类号：O175.2

DOI:10.15926/j.cnki.issn1672-6871.2016.02.019

文章编号：1672-6871(2016)02-0092-04

收稿日期：2015-12-03

作者简介：李伟(1964-),女,河南偃师人,副教授,硕士,研究方向为非线性数学物理方程.

基金项目：国家自然科学基金项目(11171227);河南省科技攻关基金项目(132102310309)