一个新混沌系统的脉冲鲁棒镇定与鲁棒同步

程　杰

(重庆师范大学 数学学院,重庆 401331)



一个新混沌系统的脉冲鲁棒镇定与鲁棒同步

程杰

(重庆师范大学 数学学院,重庆 401331)

摘要：考虑了一个新混沌系统，利用脉冲控制的方法，给出了不确定扰动的系统渐近稳定到平衡点的一个充分条件。同时，考虑了存在扰动的两个混沌系统同步问题，得到了充分判据。最后，给出了数值例子说明本文算法的有效性。

关键词：脉冲控制；鲁棒镇定；鲁棒同步；混沌系统

0引言

混沌同步在物理、保密通信、生物系统和神经网络等领域中有着广泛的应用前景。近年来，脉冲控制被广泛应用于混沌系统的稳定与同步中[1-6]，该控制方法有以下优点：控制器的设计较简单，控制装置所需成本低，控制时所需能量少。

自从发现洛仑兹系统以来，越来越多的混沌系统被构造出来，文献[7]提出了一个新的混沌系统:

(1)

其中：x1,x2,x3是状态变量，当参数a=10,b=1,c=5,d=-1,h=-5,k=-6且x1(0)=1,x2(0)=-1,x3(0)=-3时，系统(1)是混沌的。

文献[8]研究了系统(1)的脉冲控制与完全同步问题，但没考虑系统工作过程中外界干扰对系统性能的影响。本文主要研究了在有外界扰动的前提下，如何利用脉冲控制的方法来实现系统(1)的鲁棒镇定及鲁棒同步[9]。在脉冲间隔变化的情况下，得到了保证脉冲控制的有扰动的系统渐近稳定到平衡点的一些判据。最后，给出数值例子说明本文算法的有效性。

1基本定义与预备知识

一个脉冲微分系统描述如下：

(2)

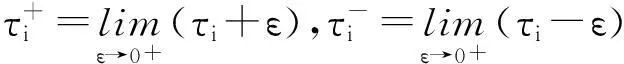
为得到系统(2)稳定的充分条件，首先介绍下列定义：

定义1设V:R+×Rn→R+，则称V属于V0类，如果

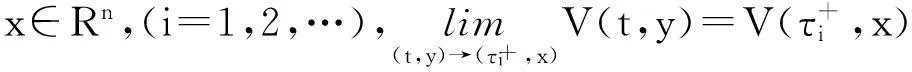
(Ⅱ)V在x是局部Lipschitz的。

定义2对(t,x)∈(τi-1,τi]×Rn，定义

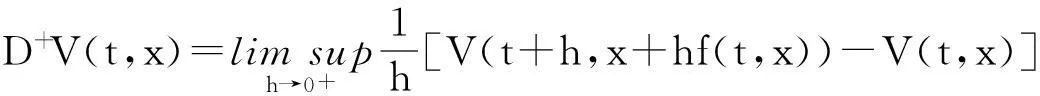
定义3 设V∈V0，且

D+V(t,x)≤g(t,V(t,x)),t≠τi;

V(t,x+Ui(x))≤ψi(V(t,x)),t=τi,

其中:g:R+×R+→R连续;ψi:R+→R+非降。则下列系统

(3)

称作系统(2)的比较系统。

定义4一个函数α(x)属于K类是指：α∈C[R+,R+],α(0)=0,α(x)是严格单调递增的。

下面介绍本文所需文献[10]中的两个定理。

定理1假设下列3个条件满足：

(Ⅰ)V:R+×Sρ→R+,ρ>0,V∈V0,D+V(t,x)≤g(t,V(t,x)),(t≠τi);

(Ⅱ)存在ρ0>0,使得x∈Sρ0时，对所有的i有x+Ui(x)∈Sρ0；对x∈Sρ0,t=τi有V(t,x+Ui(x))≤ψi(V(t,x));

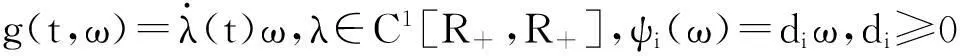
(Ⅰ)存在r>1，使得λ(τk+1)+ln(rdk)≤λ(τk)(k=0,1,…)成立;

2新混沌系统的脉冲鲁棒镇定

把系统(1)所提出的混沌系统的线性部分与非线性部分分开，重写如下：

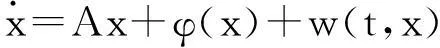
(4)

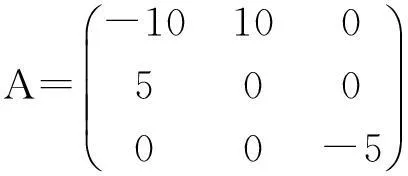
(5)

施加脉冲控制的系统可描述为：

(6)

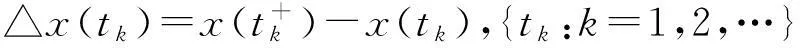
设计脉冲控制器为△x(tk)=uk(φ(x(tk)))=-ξ△tkx(tk)。

定理3设q是AT+A的最大特征值，dk=(1-ξ△tk)2，M是混沌系统的一个界，p=q+1+L2+6M，系统(1)是脉冲鲁棒稳定的，如果存在γ>1 使得:

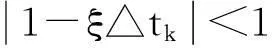
证明取Liapunov函数V(t,x)=xTx,则当t≠tk时，

D+V(t,x)=xT(AT+A)x+φT(x)x+xTφ(x)+xTw(t)+wT(t)x≤

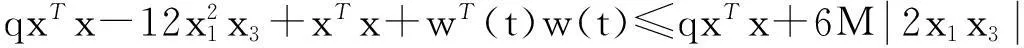
qxTx+6MxTx+xTx+L2xTx≤(q+6M+1+L2)V(t,x)=pV(t,x)。

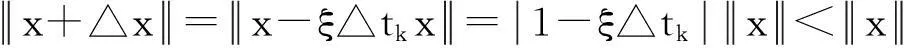
当t=tk时，有 V(tk,x+uk(y))=(x-ξ△tkx)T(x-ξ△tkx)=(1-ξ△tk)2xTx=(1-ξ△tk)2V(tk,x)≤dkV(tk,x)。

故取ψk(ω)=dkω。由文献[10]中定理可得到与系统(6)具有相同稳定性的比较系统：

(7)

由于p△tk+ln(γdk)≤0，可得ptk+1+ln(γdk)≤ptk。

根据文献[10]中定理可得：受扰动的系统(6)是鲁棒镇定的。

3新混沌系统的脉冲鲁棒同步

在同步构造模型中，驱动系统由式(4)确定，受驱系统为：

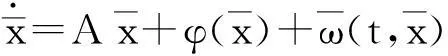
(8)

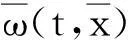
(9)

那么，同步误差系统为：

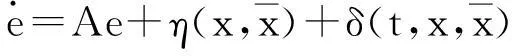
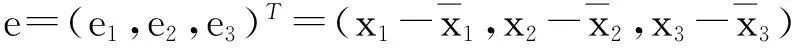
(10)

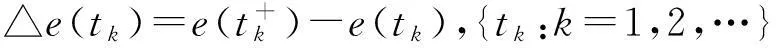
设计脉冲控制器为△e(tk)=uk(φ(e(tk)))=-ξ△tke(tk)。

定理4设q是AT+A的最大特征值，dk=(1-ξ△tk)2，M是混沌系统的一个界，p=q+1+L2+4M2+12M，系统(8)与系统(4)的脉冲鲁棒同步是渐近稳定的，如果存在γ>1 使得：

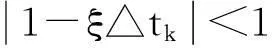
证明取Liapunov函数V(t,e)=eTe,则当t≠tk时，

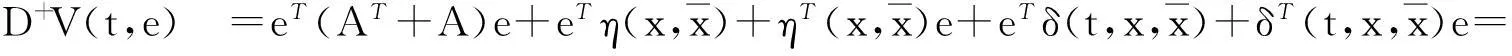
qeTe+2(2M2eTe+6MeTe)+eTe+L2eTe=(q+1+L2+4M2+12M)V(t,e)=pV(t,e)。

当t=tk时，有V(tk,e+uk(y))=(e-ξ△tke)T(e-ξ△tke)=(1-ξ△tk)2eTe=(1-ξ△tk)2V(tk,e)≤dkV(tk,e),故取ψk(ω)=dkω。由文献[10]中定理可得到与系统(10)具有相同稳定性的比较系统：

(11)

由于p△tk+ln(γdk)≤0，可得ptk+1+ln(γdk)≤ptk。

根据文献[10]中定理可得：受扰动的系统(10)是渐近稳定的。

4数值例子

例1q=2×3.660 3,M=6,选取L=1,γ=2,ξ=25,△t1=△t2=…=△tk=…=0.03，则设计的脉冲控制器为uk(φ(x(tk)))=-0.92x。

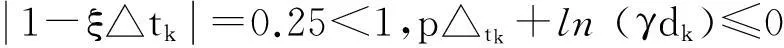
例2q=2×3.660 3,M=6,选取L=1,γ=1.1,ξ=46,△t1=△t2=…=△tk=…=0.02，则设计的脉冲控制器为uk(φ(e(tk)))=-0.92e。

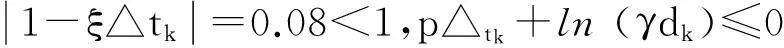
5结论

本文研究了一个新的混沌系统在脉冲控制下的脉冲鲁棒镇定与鲁棒同步问题，在脉冲间隔变化的情况下，得到了保证脉冲控制系统同步的一些充分判据，也得到了脉冲区间△的上界估计。

参考文献：

[1]胡爱花,吴昌应.基于脉冲控制的不确定混沌系统的同步[J].河南科技大学学报(自然科学版),2010,31(5):51-55.

[2]罗润梓.一个新混沌系统的脉冲控制与同步[J].物理学报,2007,56(10):5655-5660.

[3]ZHAO Y H,YANG Y Q.The impulsive control synchronization of the drive-response complex system[J].Physics letters a,2008,372(48):7165-7171.

[4]LIU G M,DING W.Impulsive synchronization for a chaotic system with channel time delay[J].Communications in nonlinear science & numerical simulation,2011(16):958-965.

[5]SUN J T,WU Q D.Impulsive control for the stabilization and synchronization of lure systems[J].Applied mathematics and mechanics,2004,25(3):291-296.

[6]方洁,陆程.非线性干扰观测器方法实现受扰混沌系统同步[J].河南科技大学学报(自然科学版),2012,33(6):35-39.

[7]ABOOEE A,YAGHINI-BONABI H,JAHED-MOTLAGH M.Analysis and circuitry realization of a novel three-dimensional chaotic system[J].Communications in nonlinear science & numerical simulation,2013,18(5):1235-1245.

[8]张群娇.一个新混沌系统的脉冲控制与完全同步[J].武汉纺织大学学报,2013,26(3):43-46.

[9]许弘雷,刘新芝.陈氏混沌系统的脉冲鲁棒同步[J].系统工程与电子技术,2005,27(3):486-489.

[10]LAKSHMIKANTHAM V,BAINOV D D,SIMEONOV P S.Theory of impulsive differential equations[M].Singapore:World Scientific,1989.

文献标志码：A

中图分类号：O415.5

DOI:10.15926/j.cnki.issn1672-6871.2016.02.020

文章编号：1672-6871(2016)02-0096-04

收稿日期：2015-05-26

作者简介：程杰(1990-),男,重庆开县人,硕士生,研究方向为微分方程与动力系统.

基金项目：重庆市自然科学基金项目(2011jjA00003)