脉冲微分方程的block-by-block方法

马群长，曹俊英，孙　涛，王自强

(1.贵州民族大学 理学院，贵州 贵阳 550025；2.上海金融学院 统计与数学学院，上海 201209)



脉冲微分方程的block-by-block方法

马群长1，曹俊英1，孙涛2，王自强1

(1.贵州民族大学 理学院，贵州 贵阳 550025；2.上海金融学院 统计与数学学院，上海 201209)

摘要：针对脉冲微分方程初值问题，首先，将脉冲微分方程转化为等价积分方程，然后，对等价的积分方程利用block-by-block方法构造了一个高阶数值格式，并分析了该数值格式的收敛性和稳定性。数值算例验证了理论分析的正确性。

关键词：脉冲微分方程；block-by-block方法；数值格式；收敛性；稳定性分析

0引言

许多反映客观现实的物理模型都具有脉冲现象，即物理模型在发展的某些阶段,由于受到外部的作用或系统内部自身的原因，使得系统瞬间改变原有的状态。脉冲微分系统能够更深刻、更精确地反映瞬间突变事物的变化规律。正因为如此，脉冲微分方程引起了国内外众多学者的研究兴趣。文献[1-2]利用Runge-Kutta方法分析了一类线性脉冲微分方程，并证明该数值方法是稳定的。文献[3]分析了脉冲微分方程的配置点法，并给出了数值算例。文献[4]利用 Runge-Kutta方法研究了具有时间变化的脉冲微分方程，并分析了格式的收敛性。文献[5]分析了二阶脉冲微分方程三点边值问题解的存在性。文献[6]分析了脉冲微分方程精确解与数值解的渐近稳定性。文献[7]分析了脉冲微分方程Runge-Kutta方法的渐近稳定性。文献[8]分析了脉冲微分方程的迭代学习控制问题。

但是，以上针对脉冲微分方程初值问题构造的数值算法的缺点是精度低、计算量大。 文献[9]对经典的block-by-block方法求解分数阶微分方程的数值格式给出了最优误差估计。 文献[10]利用修正的block-by-block方法求解二维分数阶Volterra积分方程。 本文将利用经典的block-by-block方法数值求解脉冲微分方程，主要针对线性脉冲微分方程建立了一个新的高阶数值格式，并分析该数值格式的收敛性和稳定性，最后，通过数值算例验证了数值算法的有效性。

1数值格式

考虑如下脉冲微分方程：

(1)

由文献[8]可知：当f,Ik分别满足单边Lipschitz 条件和经典 Lipschitz 条件时,问题(1)可以转化为如下等价积分方程：

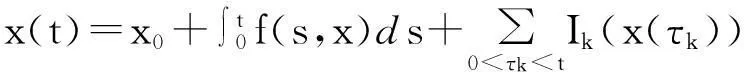
(2)

因此，由方程(1)可得脉冲项的表达式为：

(3)

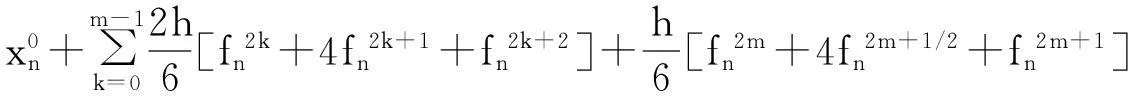
(4)

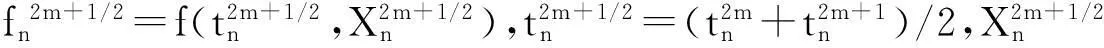
(5)

将式(5)代入式(4)并整理可得：

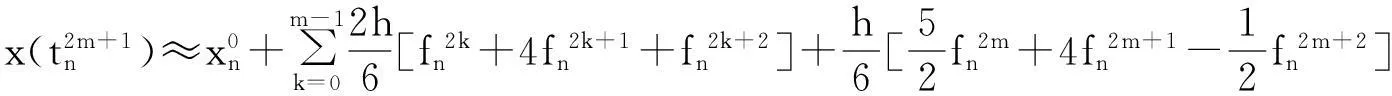
(6)

因此，第2m+1步的数值格式为：

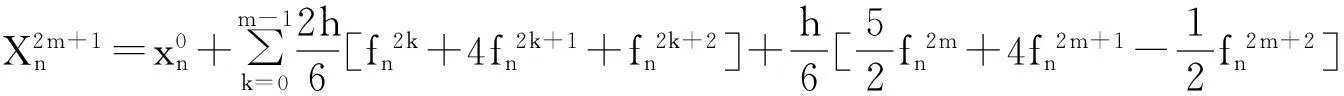
(7)

(8)

此即第2m+2步的数值格式：

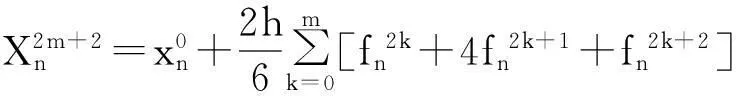
(9)

联立式(7)和式(9)，对于m=1,2,…,N-1,有如下block-by-block数值格式:

(10)

2收敛性分析

本节主要分析block-by-block数值格式(10)的收敛性。 首先，假设f(t,x)和Ik(x)关于自变量x均满足Lipschitz条件，即存在正常数L1和L2，使得：

(11)

定理1设f(·,x(·))∈C4(Ω)且满足式(11)，则数值格式(10)收敛，且其收敛精度为O(h4)。

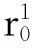
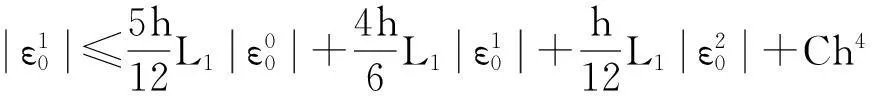
(12)

同理，

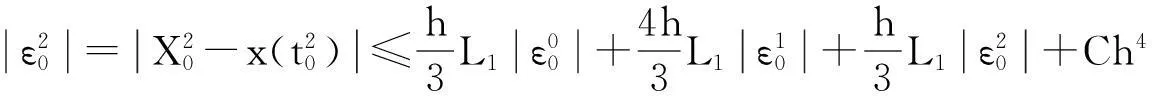
(13)

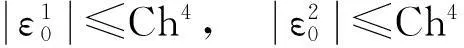
(14)

类似地，

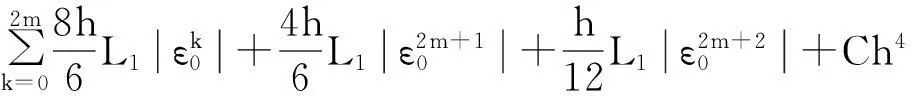
(15)

同理，

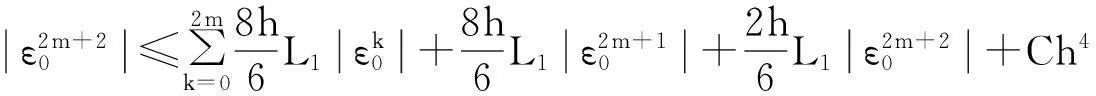
(16)

联立式(15)和式(16)可得：

(17)

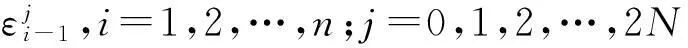
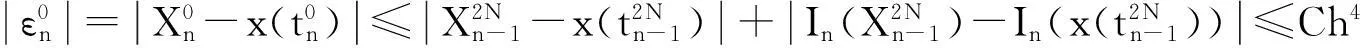
(18)

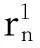
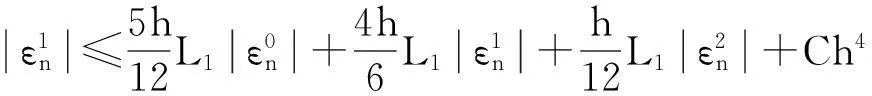
(19)

同理，

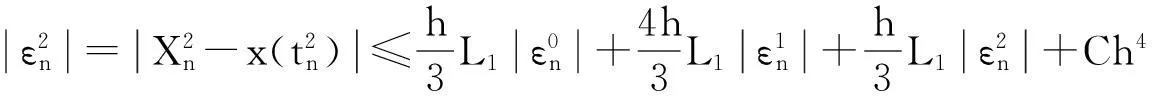
(20)

联立式(18)~式(20)可得：

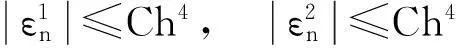
(21)

类似于式(15)的证明，可得：

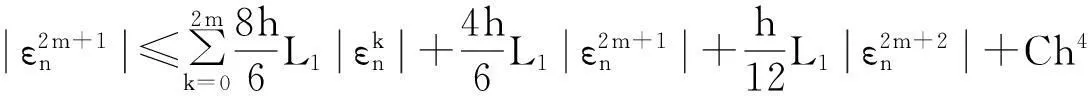
(22)

同理，

(23)

由式(22)和式(23)可得：

(24)

证明完毕。

3稳定性分析

与常微分方程一样，本节将研究右端项和脉冲项为

f(t,x(t)):=λx(t);△x(t)=Ik(x(t))=βx(t)

(25)

的数值格式(10)的稳定性，其中，λ，β为非零实数。

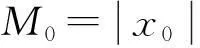
(26)

其中：C只与L2和λ有关。

证明将f(t,x(t))=λx(t)代入到数值格式(10)，有：

(27)

解方程组(27)得：

(28)

(29)

其中：A1=(12-5hλ)/[(2hλ-3)2+3]；A2=[hλ(5-2hλ)]/[(2hλ-3)2+3]；B1=(8hλ+12)/[(2hλ-3)2+3]；B2=[4hλ(hλ+1)]/[(2hλ-3)2+3]。

由式(28)可知：

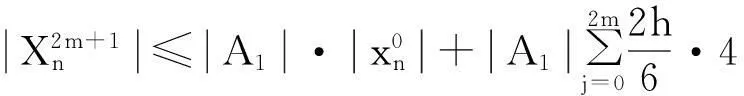
(30)

为了证明数值格式(10)的稳定性，采用数学归纳法证之，详细步骤如下：

(Ⅰ)当n=0时，由式(30)有：

(31)

再应用离散的 Gronwall不等式，可得：

(32)

其中：C只与λ有关。

同理，由式(29)可证：

(33)

(Ⅱ)假设当n=k-1时，结论成立，即：

(34)

(Ⅲ)当n=k时，

(35)

联立式(30)、式(34)和式(35)可得：

(36)

对式(36)应用离散的 Gronwall不等式，可得：

(37)

其中：C只与L2和λ有关。

同理可得：

(38)

证明完毕。

4数值算例

本节将利用前文构造的block-by-lock数值格式(10)求解脉冲微分方程。

例1考虑如下脉冲微分方程初值问题：

(39)

由文献[2]可知：该问题的精确解为x(t)=0.5e1.3{t}((1+(-0.8))e1.3)[t],其中，{t}和[t]分别代表t的小数部分和最大整数部分。

表1　最大绝对误差和收敛阶随步长h的变化

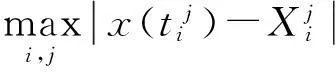
5结论

本文利用block-by-block方法，对脉冲微分方程构造了一个高阶数值格式，并证明了该数值格式具有四阶收敛精度，同时，还给出了该数值格式的稳定性分析过程。最后，数值结果验证了该数值格式的有效性。虽然本文仅考虑了一类具有脉冲项的常微分方程模型问题，但是该方法可以很容易推广到求解具有脉冲项的偏微分方程中。

参考文献：

[1]LIU M Z,LIANG H,YANG Z W.Stability of Runge-Kutta methods in the numerical solution of linear impulsive differential equations[J].Applied mathematics and computation,2007,192(2):346-357.

[2]RAN X J,LIU M Z,ZHU Q Y.Numerical method for impulsive differential equation[J].Mathematical and computer modelling,2008,48(1/2):46-55.

[3]ZHANG Z H,LIANG H.Collocation methods for impulsive differential equations[J].Applied mathematics and computation,2014,228:336-348.

[4]DIN Q,DONCHEV T,NOSHEEN A,et al.Runge-Kutta methods for differential equations with variable time of impulses[J].Numerical functional analysis and optimization,2015,36:777-791.

[5]YANG X X,WANG Z Y,SHEN J H.Existence of solution for a three-point boundary value problem for a second-order impulsive differential equation[J].Journal of applied mathematics and computing,2015,47:49-59.

[6]ZHANG G L,SONG M H,LIU M Z.Asymptotical stability of the exact solutions and the numerical solutions for a class of impulsive differential equations[J].Applied mathematics and computation,2015,258:12-21.

[7]ZHANG G L,SONG M H.Asymptotical stability of Runge-Kutta methods for advanced linear impulsive differential equations with piecewise constant arguments[J].Applied mathematics and computation,2015,259:831-837.

[8]LIU S D,WANG J R,WEI W.A study on iterative learning control for impulsive differential equations[J].Communications in nonlinear science and numerical simulation,2015,24:4-10.

[9]王自强,曹俊英.分数阶微分方程的block-by-block算法的最优阶收敛性分析[J].工程数学学报,2015,32(4):533-545.

[10]马群长,曹俊英,孙涛,等.二维分数阶Volterra积分方程的修正block-by-block方法[J].应用数学与计算数学学报,2015,29(2):162-170.

文献标志码：A

中图分类号：O241.8

DOI:10.15926/j.cnki.issn1672-6871.2016.02.017

文章编号：1672-6871(2016)02-0082-06

收稿日期：2015-08-24

作者简介：马群长(1987-),男,贵州威宁人,硕士生；王自强(1981-)，男，通信作者，河南禹州人，副教授，博士，硕士生导师，主要研究方向为微分方程数值解与复合材料多尺度分析.

基金项目：国家自然科学基金项目(11426074,11501140,11401380);贵州省科技厅自然科学基金项目([2014]2098，[2013]2144);贵州省教育厅基金项目([2013]405)