探究题目结论拓展曲线内涵

☉重庆市垫江第一中学校 严达强

探究题目结论拓展曲线内涵

☉重庆市垫江第一中学校 严达强

数学问题中通常蕴含着丰富的结论，对结论的探究可拓展我们思考问题的视角.圆锥曲线问题一直以来都是学生最为头疼的问题之一，在平时的解题训练中若善于挖掘题目中隐含的一般结论，并借助该结论解题，可减少计算过程，这对于分秒必争的高考有实际意义.本文以一道椭圆问题的题目探究为例进行说明.

（1）求动点E的轨迹C的方程；

（2）设过点F（1，0）的直线l与曲线C相交于不同的两点M、N.若点P在y轴上，且|PM|＝|PN|，求点P的纵坐标的取值范围.

（2）略.

本题的命制可追根于人教版一道教材例题：

例2如图1，设点A、B的坐标分别为（-5，0）、（5，0）.直线AM、BM相交于点M，且它们的斜率之积是-，求点M的轨迹方程.

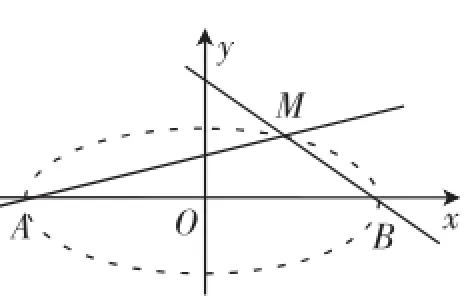
图1

由此可见，在坐标轴内，动点（x，y）到两定点（a，0）、（-a，0）的斜率乘积等于常数m（-1＜m＜0）的点的轨迹为椭圆（除去x＝±a）.

一、结论探究

图2

证明：如图2，设点A（x1，y1），B（x2，y2），P（x0，y0）（x0≠x1，x0≠x2）.

这个结论我们常称之为椭圆的第三定义.

若将A、B为顶点的条件换成A、B是椭圆上关于原点对称的两点，结论是否成立呢？

二、探究变换

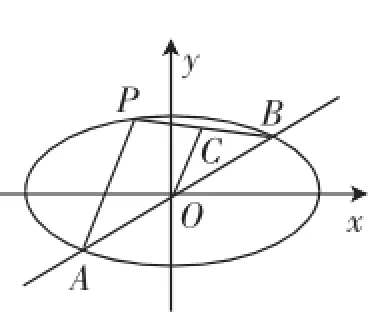
图3

解析：如图3，构造△PAB，设边PA所对的中位线为OC.设点A（x1，y1），B（x2，y2），于是所以整理得，即kAP·kOC=-.又OC∥BP，所以kOC=kBP，于是kA·PkBP=-.

三、结论拓展

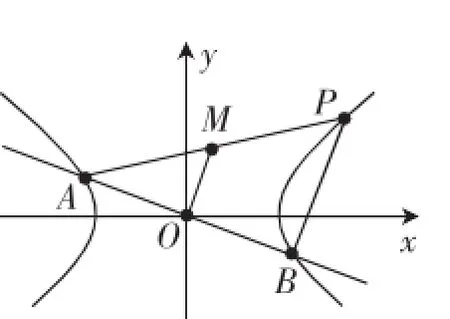
图4

解析：如图4，构造△PAB，设边PA所对的中位线为OM.设点A（x1，y1），B（x2，y2），于是所以整理得

又OM平行于BP，所以kOM=kPB，于是kPA·kPB=

四、结论应用

（1）求椭圆E的方程；

（2）过坐标原点O作不与坐标轴重合的直线l交椭圆于P、Q两点，过点P作x轴的垂线，垂足为D，连接QD并延长交椭圆于点E，试判断随着直线l的转动，直线PE与直线l的斜率的乘积是否为定值？并说明理由.

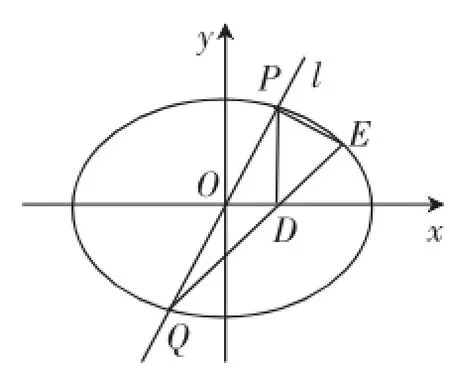
图5

（2）方法1：设直线l的方程为y=kx，P（x1，y1），E（x2， y2），则Q（-x1，-y1），D（x1，0），直线QD的斜率直线QD的方程为得，所以kPE·.所以直线PE与直线l的斜率的乘积是定值-.

方法2：设P（x1，y1），E（x2，y2），则Q（-x1，-y1），D（x1，0），

椭圆具有第一、第二定义，反映了现实中椭圆的不同生成方式，多重性正是椭圆性质的丰富体现.以上我们通过对问题的探究，从不同的视角认识了圆锥曲线，也了解了利用一些结论处理问题的方法，进而拓宽了我们解决问题的思维.F