微专题教学中实现深度学习的思考*

☉江苏省溧水高级中学 李宽珍

微专题教学中实现深度学习的思考*

☉江苏省溧水高级中学 李宽珍

一、问题的提出

新课程改革以来，“填鸭式”、“灌输式”的课堂逐步被“自主、合作、探究”等学习方式取代.学生在参与课堂，师生交流等方面有了突飞猛进的进展，但是由于高考模式的应试性，加上教师对新学习方式的理解欠缺，导致在“自主、合作、探究”等教学模式实施过程中出现了不少问题.调查发现，很多课堂是简单记忆和重复训练的浅层学习，只关注外在形式，而忽视了精神实质，学生只是“忙碌”应付各种“活动”.这样只能使学生的认知停留在表面，并未能真正深入到课堂之中，学生在整个学习过程并不能真正理解知识，提高数学能力.因此，笔者提出运用深度学习的理论来指导课堂教学.深度学习是指在理解的基础上，学习者能够批判地学习新思想和事实，并将它们融入原有的认知结构中，能够在众多思想间进行联系，并能够将已有的知识迁移到新的情境中，做出决策和解决问题的学习.深度学习注重知识间的整合、运用、迁移，是一种基于理解的学习，着重学习过程的反思，重视学习的迁移运用和问题解决.

《高中数学“微专题”教学的实践研究》，是笔者主持的江苏省“十二五”（2015年度）教育科学规划课题.该课题从某具体知识点入手，针对该知识的基本问题，整合内化知识，并进行知识迁移、运用的一种小切口教学方法，为解决高中数学教学实践中“课堂效率低下”、“专题入口偏大”和“初高中衔接脱节”等问题提供解决方案.笔者在研究过程中发现，微专题教学涉及的内容适量，知识间联系紧密，可以在学习基础知识的同时，帮学生形成良好的认知结构，活化知识的运用，提升解决问题的能力，是实现深度学习的一种有效途径和方式.

二、案例呈现

如何在问题解决中建构数学解题模块，是高中数学“微专题教学”课型研究的主题之一，为此，下面笔者专门设计了一节关于“含绝对值不等式恒成立问题”微专题课，并以此来详细阐述微专题教学在实现学习深度学习中的运用.

活动（一）学生参与，比较甄别

教师引导学生尝试解决，鼓励学生参与分析问题、参与解决问题、参与评价问题等思维活动.

师：此题为何种题型？如何解决？

生1：此题为常见的恒成立问题，可以先解出来，再根据恒成立问题的解决办法求出.

学生根据题意进行转化，展示解法：

生2：不对，不一定恒为正，所以不能用，需要讨论符号，接着给出解法：

师：两种解法得到了两种不一样的结果，谁对谁错？那么问题到底出在哪里呢？

生（众）：第二种解法对.

师：那解法1错在哪里？其本质问题是什么？

（学生思考良久，未能得出所以然）

师：此题中涉及的“或”命题的恒成立问题：对任意的x∈M，p（x）或q（x）成立.其含义包含三种情况：

（1）对任意的x∈M，p（x）成立，q（x）不成立；

（2）对任意的x∈M，q（x）成立，p（x）不成立；

（3）对任意的x∈M，p（x）和q（x）均成立.

因此，案例的解法1，错在把“∀x∈M，p（x）∨q（x）”等价于“∀x∈M，p（x）；或∀x∈M，q（x）”，未能真正理解题意.

师：根据以上分析，如何修正错误答案？

生1：还是我自己来修正吧！（大家会心地一笑）

解法3：原不等式⇔a＞x2或a＜x在x∈［0，1］上恒成立⇔原不等式的解集⊇［0，1］.

当a＜0时，原不等式的解集为（a，+∞）⊇［0，1］；

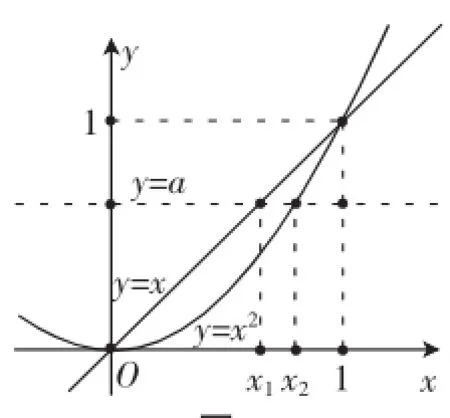
图1

当a＝0时，0不在解集中；当a＝1时，1不在解集中.故a≠0且a≠1.

故a的取值范围为（-∞，0）∪（0，1）∪（1，+∞）.

生3：（迫不及待地）也可以通过画图，如图1，根据数形结合来解决：

解法4：在x∈［0，1］的条件下，当a＞1时，a＞x2恒成立；当a＜0时，a＜x恒成立；当a∈（0，1）时，如图1，在x∈［0，x2）时，a＞x2；在x∈（x1，1］时，a＜x成立.又［0，x2）∪（x1，1］＝［0，1］，故原命题成立.

故a的取值范围为（-∞，0）∪（0，1）∪（1，+∞）.

生4：若一个问题直接解决比较困难，那也可以从反面考虑：

而x≤x2只可能在0及1时成立，代入得a＝0，或a＝1.所以a≠0且a≠1时原命题结论成立.故原命题中a的取值范围为（-∞，0）∪（0，1）∪（1，+∞）.

生：（惊呼）好简洁啊！同时爆发出一阵阵掌声.

师：万变不离其宗，各种方法的共同之处是什么？你们评价一下，哪一种解法更简单，为什么？

生5：解法二、三比较接地气，但是容易错，考虑问题不全面，解法四和五一个数形结合，一个考虑命题的否定，比较简洁，易于理解.

活动（二）引领思考，挖掘本质

师：刚才我们对不等式中的这类恒成立问题有了深刻理解，下面的问题你能解决吗？

拓展已知函数f（x）是偶函数且在［0，+∞）上是增函数，若（fax+1）＞（fx-2）在上恒成立，求实数a的取值范围.

生6：本题由偶函数及增函数的性质，原不等式可等价转化为｜ax+1｜＞｜x-2｜在上恒成立⇔｜ax+1｜＞2-x在上恒成立，这个也就是我们刚才的问题.

学生对照刚才的几种解法，可得出以下各解：

综上可得a＜-5或a＞1.

故a的取值范围为（-∞，-5）∪（1，+∞）.

生7：解法2：令f（x）＝｜ax+1｜，g（x）＝2-x，定义域均为，可画出函数y＝g（x）的图象，而函数y＝（fx）的图象过点（0，1）且在函数y＝g（x）图象的上方，由图2可知，满足-1＜-＜0或0＜-＜时满足题意.故a的取值范围为（-∞，-5）∪（1，+∞）.

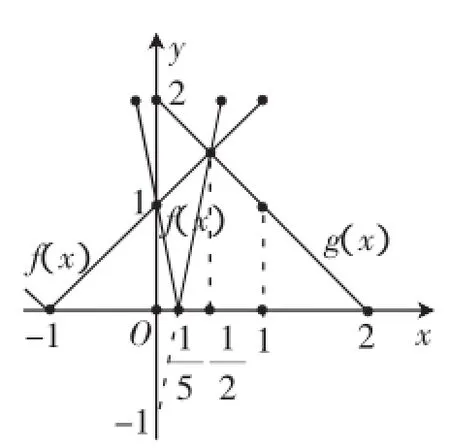
图2

故原命题中a的取值范围为（-∞，-5）∪（1，+∞）.

师：大家再想想各种方法的共同之处是什么？再考虑一下每一种解法的优劣？

（学生独立思考，相互交流）

生9：从上面两个例题分析可知，解集法易理解，但并不是所有的不等式都可轻易、清楚地写出解集，在能写出解集的情况下是个好方法；数形结合的方法简洁，需要具有一定的数形结合转化能力，但有些函数图形不好表示；考虑反面的方法既易理解，又便于操作，且很简洁，可以作为解决这一类问题的通法，而且能够较好的避免错误.

师：很好！我们在学习中就要不断的思考，善于比较解题方法的优劣，才能取得进步.

通过学生之间的讨论交流，进一步深化知识，整合方法.教师并没有止于解题的结果，而是引导学生进一步思考，判断、比较方法的优劣.让学生参与评价，能把自己的解题心得真正融入解题、说题之中，从而促进学生进行深度思考，更好地激发其学习的主动性和创造性，达到“解一题，会一类”的目的，真正做到“减负增效”.

活动（三）解后反思，拓展延伸

师：刚才大家的表现都很好！我们能否从中提炼出一个一般的结论来呢？

（学生经过独立思考，讨论）

结论1：不等式|a-f（x）|＞g（x）在x∈M内恒成立⇔a＞f（x）+g（x）或a＜f（x）-g（x）在x∈M内恒成立⇔不等式的解集｛x|a＞f（x）+g（x）或a＜f（x）-g（x）｝⊇M.

结论2：利用“正难则反”的思想，不等式|a-f（x）|＞g（x）在x∈M内恒成立⇔“|a-f（x）|≤g（x）在x∈M内有解”的参数a的取值集合，其补集即为所求.

|a-f（x）|≤g（x）在x∈M内有解⇔f（x）-g（x）≤a≤f（x）+g（x）在x∈M内有解⇔在x∈C上，［f（x）-g（x）］min≤a≤［f（x）+g（x）］max［其中集合C为不等式g（x）≥0在x∈M内的解集］.

这就是解决含参数绝对值不等式恒成立问题的通法.

师：大家可以用刚才讲的知识尝试解决下面两个问题：

练习1已知不等式|a-x|＞x2-x对x∈［0，2］恒成立，求实数a的取值范围.

练习2已知不等式x2≥2-|x-t|对x∈（-∞，0］恒成立，求实数t的取值范围.

限于篇幅仅给出答案：（-∞，0）∪（4，+∞）；（-∞，-）∪［2，+∞）.

师：以上的通法不仅能解决含参数绝对值不等式恒成立的问题，利用特称和全称、或与且、否定的转化，类似地可以解决含参数绝对值不等式有解的问题，也可以推广到p或q恒成立、有解问题，或者p且q恒成立、有解问题，同学们课后细细体会.

三、几点反思

上述微专题着重解决了含参数绝对值不等式中的一类恒成立问题，切入点小，有效针对学生的真问题进行剖析，易于学生深度学习.

（一）微专题有助于学生深度参与

深度参与是深度学习的前提，而微专题由于涉及的面小，学生易于切入问题的关键，学生的分析、讨论、探究、展示容易把握重点，不至于脱离主题，造成课堂的低效.因此微专题教学更易于学生进行知识建构和能力培养，激发学生的潜能，从而更利于学生深度参与课堂.案例中，学生各抒己见，对案例中错解的分析，以及从集合的角度、数形结合的角度，逆向思维的角度等多方面、多角度深度参与课堂.学生既有独立思考的过程，又有合作研究的机会，整个课堂融多样性和生成性于一体，给学生、教师都留有较大的思维空间，深化拓展了学生的知识.一般来说，要学生深度参与课堂，还需要注意以下几点：创设认知冲突，引起有意关注，提供原始材料，展示交流并提出个人见解，批判思维促进深度学习.案例中展示学生的解法，让学生自己去辨析、纠错，从中找出问题所在，通过学生之间的交流、讨论，深化对此处疑难点的理解.

（二）微专题促进学生深度思考

深度思考是深度学习的重点，微专题有以小见大，见微知著的特点，易于引导学生针对遇到的问题进行深入思考.深度思考注重问题的引导，通过问题的铺垫进行层层推理，进而由浅入深，由表及里的深入分析，不断深化认知、提升能力.案例中，在解决、辨析了案例中问题后，设计一道形异质同的题让学生辨别，促进学生通过现象认清本质，从而对这一类问题有更深刻的认识，对这类问题的解决方法有了深刻的思考.在学生用多种方法解决问题后，教师又引导学生比较几种方法的优劣，从而总结出此问题中运用问题的否定和数形结合解决是更简洁的方法，使学生的认识得到升华，理解得更深刻.题中所涉及的方法都是学生在问题的不断深入，不断形成认知冲突情况下得到的.学生既独立思考又合作交流，通过反复打破学生的认知平衡，促进学生思维向更深处发展，从而形成对问题深刻的洞察力和持久的理解力.

（三）微专题引领学生深度反思

深度反思是深度学习的延伸，微专题的特点以小见大，以点带面的特点利于学生进行深度思考.深度反思是基于教师对学情的理解，对教材的把握，对教学的系统设计.深度反思的关键是教学问题能否按逻辑关系形成问题链，是否按认识水平提供方法论，而在教学实践中不少教师只注重解决个别、孤立的问题，不注意引导学生发现问题的内在联系，就不能及时引导学生深度反思.微专题在教学过程中能及时反馈，针对学生出现的问题及时深度反思，有助于学生形成良好的数学认知结构.案例中，教师完成解题后没有结束本题教学，而是通引导学生对问题进行深度反思，学生在思维的调整过程中提炼出一般结论，提高了学生的探究问题的能力，培养了学生的问题意识.

深度学习的核心是要让学生体验并感悟参与的快乐，思考的深刻，反思的深化.另外，深度并非指盲目求深、求难，深度的把握是在大多数学生理解的基础上再增加一定的难度，在学生的最近发展区，让学生“跳一跳，能够摘到桃子”.深度的关键在于适时点拨，时时参与，深度思考.而微专题教学强调“大处着眼，小处着手”，提倡有针对性、选择性的教学，能针对问题节点，引领学生深度参与，深度思考，深度反思，因此，微专题教学是实现学生深度学习的一种有效途径.

1.石向阳.解恒成立问题，谨防“或”惹“祸”［J］.湖南教育（下），2015（12）.Z

江苏省“十二五”教育科学规划2015年度课题：高中数学“微专题”教学的实践研究；基金项目编号：D/2015/02/165.