高三一轮复习要把握“四度”

☉湖北武汉华中科技大学附属中学 李青林

☉湖北武汉华中科技大学附属中学 杨宇

高三一轮复习要把握“四度”

☉湖北武汉华中科技大学附属中学 李青林

☉湖北武汉华中科技大学附属中学 杨宇

前不久，因为广西柳铁二中老师要来华中科技大学附属中学交流，为此李青林老师上了一堂高三一轮复习课——一元二次不等式及其解法.课后两所学校的老师在一起探讨交流如何上好高三一轮复习课.笔者将其整理成文，与广大读者共同探讨.

一、课堂实录

师：今天我们来继续复习一元二次不等式及其解法，首先我们看一个例题.

例1解关于x的不等式-2x2+x+3＜0.

师：这是一个解一元二次不等式的问题，那么什么叫一元二次不等式？一元，是指什么？二次，是指什么？（结合学生的回答板书）

师：那么这样的不等式怎么解呢？

生1：令-2x2+x+3＝0，用因式分解的方法求方程的根.

师：两根分别是多少？

师：她之所以难以抉择，是因为二次项系数为负，容易犯错.那么我们应该怎么做？

师：不等式的解集为何不是两根之间？

生1：画二次函数图像，结合图像可以看出原不等式的解集应该是两根之外.

师：非常好.从她的解答过程我们能体会到二次方程、二次函数、二次不等式之间的关系密切，三者之间到底有什么样的关系呢？（结合学生的回答板书）

师：继续回到我们的这个例题中来，通过生1的解答我们总结一下解一元二次不等式的一般步骤是什么？（通过学生的回答板书）

师：有了这种解题步骤，我们来练习两个小题.

变式1：解关于x的不等式：x2-（3+a）x+3a＞0.（学生板演）

生2：因为x2-（3+a）x+3a＞0，所以（x-3）（x-a）＞0.

①当a＜3时，x＜a或x＞3，不等式的解集为｛x|x＜a或x＞3｝；

②当a＞3时，x＜3或x＞a，不等式的解集为｛x|x＜3或x＞a｝.

师：你讨论了a＞3，a＜3，那么还少了哪一类？

生2：当a＝3时，不等式为（x-3）2＞0，不等式的解集为｛x|x∈R且x≠3｝.

师：非常好，补充之后解答就完整了.变式1中如果将后面的a移至二次项系数，即ax2-（3+a）x+3＞0，那么我们要如何讨论呢？

生3：关注二次项系数是否为0，以及正负，还有两根的大小.

师：很好，对于含参的不等式的解题步骤同上，但我们经常要讨论：①二次项的系数；②判别式的正负；③两根的大小.（教师板书补充）

变式2：已知一元二次不等式f（x）＜0的解集为｛x|x＜-1或x＞｝，则（f10x）＞0的解集为________（.学生板演）

师：我们再看变式2，它是一个逆向问题，该同学的解法我们可以看到他始终抓住了二次不等式的解集、二次方程的根与二次函数的零点之间的联系，注重了数形结合.

例2设函数f（x）＝mx2-mx-1.

（1）若f（x）＜0的解集为R，求实数m的取值范围.

（2）若f（x）＜-m+5对任意x∈［1，3］恒成立，求实数m的取值范围.（两名学生同时板演）

师：这个函数一定是二次函数吗？为什么？

生5：不一定.当m＝0时该函数不是二次函数.所以要讨论.当m＝0时，满足题意；当m≠0时，该函数是二次函数，解法如上.综上-4＜m≤0.

师：非常好.我们注意到这里的解集为R，换句话说就是对∀x∈R，f（x）＜0恒成立.同样是恒成立问题，我们来看生6的解答过程.

生6：将不等式化成mx2-mx+m-6＜0，当m＝0时，满足题意；当m≠0时，令g（x）＝mx2-mx+m-6，并整理成g（x）＝（x2-x+1）m-6，将g（x）看成关于m的函数，只要即可，解得m＜.

师：为什么只需要1和3对应的函数值小于0就可以了呢？

生6：因为x2-x+1的对称轴为x＝∉（1，3），所以函数在此区间为单调函数.

师：有了生6的这种解释以后，上述解答过程就比较完整了.从生6的解答过程我们可以看到，他将恒成立问题转化为函数的最值问题.对于恒成立问题我们还有哪些常用解法？

生7：分离参数.

师：这个问题我们能分离参数吗？

生7：可以.由题意得原不等式可以转化为mx2-mx-1＜-m+5，故m（x2-x+1）＜6.因为，所以，因为x∈［1，3］，所以φ（x）＝φ（3）＝，所以m＜.min

师：通过以上讨论，我们发现逆向问题可通过以下几种方法解决——①三个“二”的关系；②转化为函数的最值问题；③分离参数.（教师继续板书）

师：有了上述方法，你能解决如下问题吗？

（3）若f（x）＜0对任意m∈［-1，1］恒成立，求实数x的取值范围.

（4）若f（x）的值域为（-∞，0］，且关于x的不等式f（x）＞c的解集为（t，t+5），求实数c和t的值.

生8：把m看作是自变量.

师：非常好.那么原函数表达式可看成是关于变量m的什么函数？此函数小于零恒成立需要满足什么条件？

生8：一次函数，两个端点的函数值小于0就可以了.即令h（m）＝mx2-mx-1＝（x2-x）m-1，令

师：解决第（4）小问之前，首先思考一个问题：f（x）＜0恒成立与f（x）的值域为（-∞，0］有区别吗？

生9：f（x）＜0恒成立即函数f（x）的图像恒在x轴下方，f（x）的值域为（-∞，0］，即函数f（x）的图像与x轴相切.

师：回答得很好，这个问题留给同学们课后解决.

师：本节课你学到了什么知识或数学思想方法？你能总结一下吗？请把你的总结写在草稿本上.

师：李老师也对这节课进行了一个框图式的总结，现跟大家分享一下（课件展示如图1）.

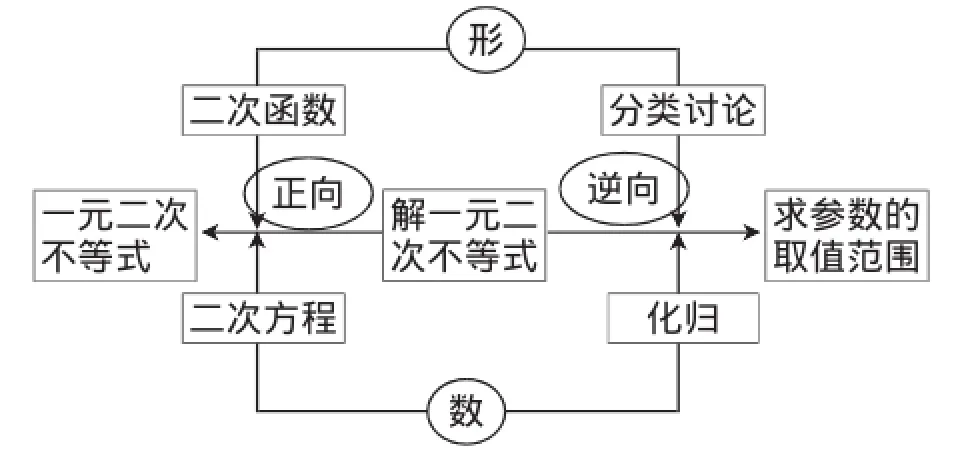
图1

二、专家点评与课后反思

高三一轮复习课要有“四度”.

1.坡度

人们常说一个好的老师必需尊重学生、关爱学生.尊重学生、关爱学生不仅要体现在对学生文化成绩、身体健康与心理状况上的关注，更要体现在课堂上如何尊重学生、关爱学生.因为学生有个体差异，教师精心设置出低起点、又层层递进的课堂是真正关爱学生的体现.苏霍姆林斯基说过：“人的心灵深处都有一种根深蒂固的需求——这就是希望自己是一个发现者、研究者、探索者.”设置好了坡度，便是给学生提供了一个台阶让其成为发现者、研究者、探索者.本节课例题的设置由浅入深，问题的提出从易到难.让所有学生的思维都能动起来，又不会轻而易举地解决问题，形成一种金字塔式的思维上升的模式.

2.深度

数学课堂是一种重视思维的课堂，思维的训练是通过题目为载体的，离开了例题就谈不上什么方法，所以例题的选取对整堂课起着很重要的作用.数学课堂又不仅仅做题.光是习题的堆砌学生不会有太大的收获，充其量是刷题，所以，一堂好的复习课必须要有深度.要使一节复习课有深度，除精心选题外，更主要的是解题后上升到一种思想方法.如果说好的例题是一杯白开水的话，那么思想方法的总结就是白糖，只有加入适量的白糖，水才会甘甜.本节课从例题中提炼知识和方法，水到渠成.正所谓“题不在多，有思则灵，法不在全，有度则深”.但是“深度”不是“难度”.本节课从一个简单的问题小结出解一元二次不等式的步骤，从学生的解答过程中体现出由数到形、由形又到数的数形结合思想，在展示学生错误的解法过程中引起了认知冲突，挖掘了转化与化归的思想.一节课有了思维冲突，才有深度；有了深度，才有内涵；有了内涵，才有味道.

3.高度

许多老师对数学的理解有独特见解，但只顾着自己讲题过瘾，给人的感觉便是老师到了“会当凌绝顶，一览众山小”的高度，而“学生却云深不知处”，最后只剩下老师“高处不胜寒”.究其原因，老师过多地代替学生思考、代替学生讲解、代替学生总结.而高三的学生基础知识都已经学习过，一轮复习主要是夯实基础，形成知识网络，建立联系.只有这样，学生才能真正地体会到登到山顶的痛快.课堂小结无疑是学生建立联系的好的机会，何不把这样的机会让给学生.不管他总结得是否全面，是否完美，但只要认真想，他自己的结果往往比老师的总结更有帮助.本节课教师先给学生一个思想升华的空间，然后与学生一起分享自己的成果，在和学生平等的前提下共同提高.教师做到了站得高看得远，真正落实了以学生为主体，以教师为主导的教育思想.

4.精度

数学语言的最大特点就是严密与精炼.斯托利亚在《数学教育学》一书中指出：“数学教学也就是数学语言的教学.”教师在教学过程中，要想将抽象、严密的逻辑推理过程直观形象地表现出来，数学语言作为一种科学语言工具，它是数学的载体，通过它，师生共同学习，探索数学规律，领会数学知识，会更加简单而快捷.因此，一方面，教师讲课的时候要注意数学语言的规范使用，通过数学语言的交流使学生对数学问题由浅入深、由表及里、由特殊到一般地去仔细品味，透过现象看本质，使他们有机会由感性认识上升到理性认识，由实践到认识产生质的飞跃.另一方面，在给学生讲解的过程中，要特别重视语言的准确、严密，引导学生用科学的语言进行叙述，对学生形成潜移默化的引导；学生在讨论、回答问题时也运用数学语言，不断增强运用数学语言的能力，课堂的实效性才会真正地得到提高.本节课教师的语言不是特别的精炼，有时略显啰唆，可以进一步提高.

（本文的撰写感谢华中科技大学附属中学和广西柳州铁二中的老师的点评和意见）

1.杨爱云，蔡小雄.数学复习课应有的“二味”“三度”［J］.数学通讯，2015（4）.

2.王晓苏，“好”题还要讲“好”——高三数学复习课教学的一点体会［J］.中学数学（上），2015（4）.F