读懂教材剖析概念渗透思想——以“点到直线的距离公式”为例

☉甘肃天水市第一中学 宫前长

读懂教材剖析概念渗透思想
——以“点到直线的距离公式”为例

☉甘肃天水市第一中学 宫前长

章建跃博士对数学教师备课提出要做到“理解数学、理解学生、理解教学”.数学备课就是在理解教材编写意图的基础上，备好数学知识的逻辑生成关系和过程，深刻挖掘蕴含在教材中数学知识的内在结构和联系，凸显例、习题的教学功能与价值，透视和领会深藏在数学概念、公式和例题等中的数学思想方法，才能称得上读懂了教材.唯有这样才可以备好数学课，解决“怎样备”和“备什么”的问题，给课堂教学的有效性提供坚实的基础.

一、备：教材的编写意图

人教A版《数学》（必修2）第三章第3节“点到直线的距离公式”是解析几何中的重要概念，在教材中占有重要的地位，在其中蕴含着重要的数学思想方法，因为它是基于有着丰富数学思想方法的“两点间的距离”的概念，又能够方便、自然地引出“平行线间的距离”的概念，其教育的地位、桥梁作用是不言而喻的.

1.剖析课标

《普通高中数学课程标准》对“点到直线的距离公式”的内容要求：“探索并掌握——两点间的距离公式、点到直线的距离公式，会求两条平行直线间的距离.”“点到直线的距离公式”是处于中间位置，具有“桥梁”的作用，容易将“两条平行直线的距离”转化为“点到直线的距离”来解决，充分突出了探究“点到直线的距离”的途径、方法与策略是本节的重点和关键之处.课标要求全方位地体现解析几何的本质：用代数方法来研究几何问题.从而可知，本节重点是点到直线的距离公式的建立和探究，难点是选择适当的思维方式方法解决问题.

2.“距离”认识的直观性

数学教材对距离的解读：小学是从实际问题进行感知“距离”大小远近；初中是从“形”的直观性入手，让学生认知和理解“距离”；高中是从“数”的精细化掌握和计算“距离”.

因此，平面内静态的“距离”理解、动态的“距离”理解具有较大的思维空间差异，甚至空间中的静态和动态“距离”理解等都源于直观性的认知基础，可见“距离”的直观性感知、理解就显得非常重要.

点到直线的距离公式教学不能只满足于告诉学生这个公式“是什么”或“什么是”，还应该让学生了解点到直线的距离公式的背景、引入的理由，知道公式的建立、发展或解决问题中的作用和意义.

3.突出“距离”的主线作用

学生已经学习了两点间的距离公式，直线的倾斜角和斜率，直线方程的几种形式，直线间位置关系判断的依据，经历了建立直角坐标系解决问题的过程，积累了一定的学习经验和操作方法，在适当的时机提出“距离”问题，回顾初中所学的两点间的距离、点到直线的距离和平行线间的距离，并且加以区别，寻找共同点，成为促进探究点到直线距离公式的逻辑必然性.

点到直线的距离公式教学，是以“距离”问题为主线解决点到直线的距离，突出数学公式的发现、探究公式的证明过程和理解公式价值的心理过程为基本线索，以学生数学知识最近发展区为引入距离的必要性.课堂探究活动中要尊重学生的思维过程，充分发挥学生在学习中的主动性，搭建合作、交流的学习平台.

二、读：知识的内在结构和联系

1.弄清最近发展区的知识

有效教学源于学生的最近发展区的教与学，学生经历了初中数学的学习，从“形”的视角很容易理解点与点之间的距离、点到直线的距离，从“数”的层面只是会计算点与点之间的距离.高中在“直线与圆的方程”一章学习了直线的倾斜角、斜率、直线的位置关系及两点间的距离公式.但要计算点到直线的距离需要在教材所展示知识和方法的基础上，进一步的分析、思考，让学生独自思考后，再小组讨论和完善，概括形成公式化.

2.剖析概念发挥教育价值

“点到直线的距离公式”是解析几何中的重要内容，是研究几何问题的重要工具.主要涉及点、直线，方法凸显了“数”的计算操作功能，即用代数方法解决几何问题，比起从“形”的视角（点到直线的距离即为点到直线的垂线段的长度）理解操作方便.

备课时尽力在平面内深刻剖析“点到直线的距离”的各种表征，从学科的高度和广度把握“点到直线的距离”的理解：距离是属于长度度量范畴的具体化，明确知识的发生、发展是有规律可循的，是按照人的认识规律来循序渐进的.对距离具体化认识是：“点与点的距离”“点到直线的距离”“直线到直线的距离”“点到曲线的距离”“点到区域的距离”等概念的发生、发展过程，进一步强调了数学知识的系统性和一定的逻辑性.从而让学生经历“点到直线的距离公式”的探究过程，不但强化了思维能力，而且促进了学生的能力、意志品质的发展.

3.梳理知识发展逻辑

在教材中，完全依照点的坐标、直线的倾斜角和斜率、直线方程和位置关系来呈现知识发展的逻辑顺序后，进一步研究两点间的距离公式，紧接着研究点到直线的距离问题.学生会自然想到点到直线的距离的定义，从“形”入手进行分析、思考，在坐标系中如何将点到直线的距离“坐标化”？如何刻画和表示？这一些是学生困惑不好解决的问题，点到直线的距离计算成为思考的重点.

问题的提出和思考，显得自然而然.只是采取什么方法去解决、采用什么策略去转化等需要回归教材，反复读教材，读懂概念，挖掘蕴含其中的思路：过直线外一定点作该直线的垂线，求得定点与垂足之间的距离；形成可操作的具体方法步骤：求得垂足的坐标，利用两点间的距离公式来计算.其中涉及直线方程的求法、两条直线垂直的关系.依照初中所学平行线的性质：平行线间的距离处处相等，可容易知两条平行线的距离的计算思路和方法，这一串的逻辑思维进展和探究操作，显得自然天成、浑然一体，没有一点“牵强”之味.

4.教材探究方案剖析

值得注意的是教材（第106页）给出：“上述方法虽然思路十分自然，但具体运算需要一定的技巧.”教材给出的探究方案：“根据定义，点P0到直线l的距离d是点P到直线l的垂线段的长.”

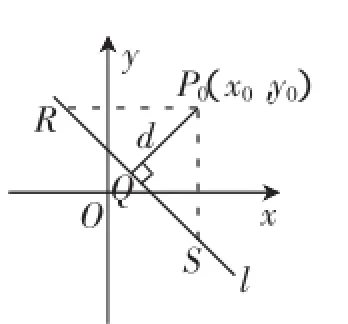
图1

如图1，设点P0到直线l的垂线段为P0Q，垂足为Q，由P0Q⊥l，可知直线的斜率为（A≠0），根据点斜式写出直线P0Q的方程，并由l与P0Q的方程求出点Q的坐标；由此根据两点距离公式求出｜P0Q｜，得到点P0到直线l的距离为d.明确提出此方法虽思路自然，但运算较繁.具有“双刃剑”的作用：提示此思路可以想，但不可以具体操作，因为太繁、难和技巧性强；或提醒意志力强的学生不畏艰难，试一试到底有多“难”，增强学生学习数学的信心，提高数学运算能力.

三、显：例、习题和旁白的教学功能

教材例、习题是编写专家进行认真思考、严格筛选的.例题教学是数学教学必不可少的重要环节，讲解例题一定要发挥其教学功能，促进沟通与所学知识的联系.学生通过习题演练能够让所学知识系统掌握、正确运用和锤炼能力，明白习题所含知识意图就是运用知识解决所学问题，才能彰显习题教育价值.

1.解读教材旁白

教材在学生思维的最近发展区设置一个思考问题：“如图1，已知点P0（x0，y0），直线l：Ax+By+C=0（A、B不同时为零），如何求点P0到直线l的距离？”对学生的数学思维具有提示、启发作用，诱导学生思考和探究数学活动，促使在课堂活动中经历、观察、猜测、推理、交流和反思等数学理性思维，切实改进学生的学习方式方法.同时又设置了2个“？”（旁白），即“试一试，你能求出|P0Q|吗？”“当A=0或B=0时，上式公式是否成立？”其目的就是有意提升学生思维能力，深刻理解公式在特殊情况下的适用性，进一步促进学生思维跟进，强化数学理性思维能力.

2.例、习题的教学功能

设置了例5（直接应用公式解决）、例6（根据点到直线的距离公式、面积公式解决）两道例题，在每一道例题的边空处提出一个“？”（旁白），有意提醒学生多观察、多思考、多分析，尽可能多地掌握解决问题的方法，如例6也可以采取面积割补的方法计算△ABC的面积，拓展学生的思维空间，提高学生解决问题的能力.

学生分小组探究例6可用其他方法解决问题后，教师应该马上提出将三角形的顶点坐标一般化，即A（x1，y1）、B（x2，y2）、C（x3，y3），能否推导出三角形的面积S的一般结论.这样做可以让学生运用所学知识，重新思考三角形面积的计算策略，有意训练思维能力和字母运算能力，学生通过合作、交流、展示所推得三角形的面积S=（|x-x）（y-y）-（x-x）（y-y）|.又一次将学生的思维31212131向前推一把，学生亲历独立思考、合作、探究、交流展示的过程，学生逐步认识问题的本质，理解得更加深刻，挖掘习题潜在的教学价值.

现行教材后面安排练习题和总复习题，目标是综合运用所学知识加以解决的数学问题，教学时一定要认真研究这一些习题的解法和变式，以拓展学生思维的深度、广度，从一般性的结论中感知、领悟数学知识的本质，感受数学教育价值意图表现出来的数学式子统一美、简捷美、奇异美和内在美.例6中三角形的顶点一般化后，其面积结论为：S=（|x-x）（y-y）-（x-x）（y-y）|，31212131还有计算方法所显示的简单，都属于数学美的范畴.前面探究所得的点到直线的距离公式自身具备上述的“四美”特征.

学生在数学活动中掌握知识的多少、理解数学的多少等与课前教师所做的“深刻”备课有很大的关系.教师只有读懂教材概念、意图，精心设计数学活动，深刻领悟教材内容、例习题意图，才能发挥教材的教育功能.

3.研究学生调整教学方法

教学时，弄清学生，准确定位学生的现有认知水平和知识经验基础，定位学生的最近发展区，精确定位每堂课知识的生长点.强调点到直线的距离概念和公式建立的重要性，消除只重视公式解题训练而忽视基础与过于重视基础知识记忆、训练为主的两种弱化能力培养的现象，强化公式建立的探究过程，加深公式的理解，从学生新的视角重新认识，促进学生在公式建立探究过程中的认知飞跃，完善点到直线的距离公式探究的思维整合，引导、帮助、合作与交流中找到解决问题的方法，在建立知识间联系的过程中领悟数学本质，争取求悟、求变的动态中提高思维能力.

教师的“教”是为学生的“学”提供启示、解疑和点拨，研究学生自然成为有效课堂教学的基点，以学生发展为本，给学生足够多“思考”的时间，给学生搭建“讨论”的平台，让学生独立思考，合作探究，真正让学生不再“套公式”，跳出“题海”练数学题，教给学生方法，学概念、思解法、练思维、习操作技术，实现高效课堂.

四、透：数学思想方法

1.教材内容中的思想

点到直线的距离公式一节，教材就已经突出了数学思想方法.点到直线的距离的理解要求对所涉及点、直线的位置有两种：点在直线上，点不在直线上.不论从“形”的直观性理解：过点作直线的垂线，点到垂足的距离即是；还是从“数”的可算性（坐标化）理解：一点与直线上一动点的距离转化为坐标的计算最小值问题，都体现了数形结合、分类讨论和函数思想的意义和作用，即把“距离”问题具体化、特殊化处理，体现了降维思想，建立了点到直线的距离公式，有利于点到直线的距离本质的理解和掌握.

2.教学中渗透方法

点到直线的距离公式的学习处于两点间的距离公式学习之后，有着凸显解析几何的思想作用，在预设时，需要思考：为什么要研究点到直线的距离？怎样研究？带着问题读教材，为了指导学生方法读教材.形成大数学的框架理解点到直线的距离，从画图中感知点到直线的距离，从定点到直线上的动点距离动态中挖掘点到直线的距离的精细化，从坐标系中掌握点到直线的距离的计算准确化，从各种思维视角强化点到直线的距离的多样化.

3.思想定方案，方法可选优

点到直线的距离公式是一个非常重要的公式，在数学学习中有着重要的作用.其探究思路比较多，贴近学生知识有以下三种策略方案：根据点到直线的距离的概念，容易想到过点P作直线l的垂线，垂足为Q，写出该垂线的方程，再与直线l的方程联立，求得垂足的坐标，再根据两点间的距离公式求得|PQ|；利用点关于直线对称点，再根据两点间的距离求得；借助初中所学的“平行线间的距离处处相等”来求得等这一些都是学生最近发展区容易想到、方便操作的简捷思路.其具体方法如下：

已知点P0（x0，y0），直线l：Ax+By+C=0（A、B不同时为零），如何用x0、y0、A、B、C表示点P0到直线l的距离.

思路1：（定义法）过点引直线的垂线，求垂足坐标，把问题转化为两点之间的距离，此思路容易想到，实际操作、运算推理烦琐.

方法1：过点P0作直线l的垂线，垂足为点Q.

若直线l垂直于x轴，即B=0，此时直线l的方程为x= -（A≠0），故点到直线l的距离

若直线l不平行于x轴，不垂直于x轴，则直线l的斜率k=-，此时直线的方程为y-=-（x-x），即Bx-0Ay=Bx0-Ay0，与直线l的方程Ax+By+C=0联立，解得

根据两点间的距离公式，可得|P0Q|=

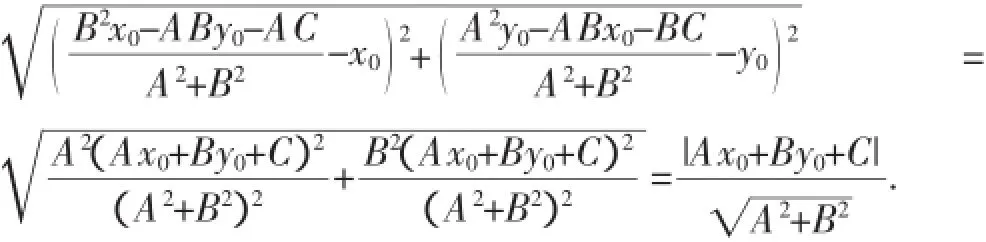
故点P0到直线l的距离

思路2：（对称性法）作点关于直线的对称点，把问题转化为两点（两个对称点）之间的距离，此思路容易想到，运算也烦琐.

方法2：直线l：Ax+By+C=0（A、B不同时为零）外一点P0（x0，y0），则点P0关于直线l对称的点为M（xM，yM），根据对称性的性质，可得解得

根据两点间的距离公式，可得|P0M|=

故点P0到直线l的距离

思路3：（平行线特殊点法）过点作直线的平行线，根据平行线间的距离处处相等，依据“距离”寻找特殊点，把问题转化为两点（两个特殊垂足）之间的距离，此思路容易想到.

方法3：设过直线l：Ax+By+C=0（A、B不同时为零）外一点P0（x0，y0）与直线l平行的直线m的方程为Ax+By+D= 0，则Ax0+By0+D=0，从而可知直线m：A（x-x0）+B（y-y0）=0.

若直线l不平行于x轴，也不垂直于x轴，则直线l的斜率k=-，此时存在与直线l、m都垂直的直线n：y=x，垂足分别为E、F，其坐标分别是根据两点间的距离公式，可得

若直线l垂直于x轴，即B=0，此时直线l的方程为x= -（A≠0），直线m的方程为x=，则直线l、m都垂直于x轴，垂足分别为，此时

综上所述，点P0到直线l的距离

点评：思路3有利于平行线间的距离公式的建立和探究，既可以理解点到直线的距离公式，又可以因势利导得到平行线间的距离公式，一举两得.

以上三种思路方法，“贵”在有法可依、可操作.虽然各种资料（杂志、教辅）上推导点到直线的距离公式的方法很多，但要明白处于学生知识最近发展区的思路方法才是好策略，否则容易想到但不好操作，或不容易想到而容易操作的策略只能作为数学思维欣赏而已.学生只有经历不同的数学活动，才能感悟到数学思维功能的博大精深！

4.基于育人的数学活动

数学公式课堂教学的重点就更应突出公式的发现、探索和证明的过程，这一数学活动过程中蕴含着育人的价值，尤其是让学生不断探索、发现、思考、确定思路方案和具体的操作流程，不断的采取验证、完善，最后形成切实可行的点到直线的距离公式证明方法，数学公式的教学，是让学生了解和经历公式的探究过程成为思维提升、思维训练的良好素材，增强每一位学生解决问题的信心、锤炼坚强的毅力和锲而不舍的探究精神，充分发挥学生独立自主的学习能力，有利于学生长远的发展和成长.

总之，读懂教材中的数学概念，才能立足于整体把握点到直线的距离公式建立的探究过程，促使问题的提出自然、顺畅，推理探究方案的选择合情合理，数学思维层次的深刻性得到更大幅度的提升，真正在问题的探究、解决中落实了数学的育人功能，发挥数学的教育价值.

1.宫前长.读懂教材之意体悟理念之真——记“数列”第一课时教学的心路历程［J］.中学教研（数学），2012（10）.

2.宫前长.新课程古典概型教学：困惑、解惑与感悟［J］.中学数学（上），2014（5）.

3.宫前长.设计合理“亮”思维追求高效“启”智慧——记“线面平行”（第一课）教学的思维历程及教学取向［J］.中学数学（上），2015（1）.F