自适应事件驱动下T－S模糊系统的控制器设计

张媛媛

(南京财经大学应用数学学院，江苏南京210046)

自适应事件驱动下T－S模糊系统的控制器设计

张媛媛

(南京财经大学应用数学学院，江苏南京210046)

T－S模糊模型的实质是任何连续函数均可由一系列IF－THEN规则模糊逼近，因此它可用许多线性系统的分析方法研究，是非线性系统建模的重要工具，近年来，很多学者用T－S模糊模型研究非线性网络控制系统，为了节省有限的网络带宽资源，事件触发机制在网络控制系统的研究中得到了广泛的应用，这些研究成果具有重要的理论意义.然而，目前的结果中将事件触发机制用于T－S模糊系统的研究尚不成熟，基于自适应事件触发机制设计控制器尤其具有重要的意义.本文在事件触发机制的基础上介绍了自适应事件触发机制，并将其应用于控制器的设计，基于具有时滞的T－S模糊系统，提出了自适应事件驱动下的控制器设计新方案，在主要结果的证明中引用一种新Lyapunov－Krasovskii泛函和自由权矩阵，并应用Schur补引理等方法处理非线性矩阵不等式，然后通过求解线性矩阵不等式，设计了理想的控制器.最后，仿真验证了设计方案的有效性.

自适应事件触发机制;T－S模糊系统;控制器;时滞

1 引言

近年来，T－S模糊系统的稳定性分析和控制器设计引起了广泛的关注，使得T－S模糊系统的研究有了进一步的发展.文献［1］中，作者利用并行分布补偿的概念提出T－S模糊闭环系统的稳定设计方法，把稳定性分析等价于线性矩阵不等式问题，此后，该方法得到广泛应用，使得系统的稳定性分析和其他性能指标的设计都可以统一到一系列等价的LMI凸优化问题中，为建立模糊控制理论的发展奠定了基础.文献［2］中，针对一类具有范数有界时变参数不确定性的非线性系统，采用T－S模糊控制方法并结合闭环系统动态性能的考虑，结果得到所设计的控制器使系统具有良好的稳态性能.文献［3］中，对具有连续时滞的T－S模糊系统，考虑到在推导过程中常被忽略的有用项可能带来保守性这一问题，构造适当的Lyapunov－Krasovskii函数，得到了开环模糊系统时滞相关渐进稳定的充分条件.然后根据并行分布补偿算法，设计了状态反馈控制器，得到了闭环系统时滞相关渐进稳定的充分条件.文献［4］中，基于T－S模糊模型，研究了同时具有输入时滞和状态时滞的模糊系统的稳定与镇定问题.文中通过构造Lyapunov－Krasovskii泛函，并结合自由权矩阵，基于线性矩阵不等式的可解性，给出了时滞相关意义下控制器设计的新方案.文献［5］中，利用T－S模型研究了时滞下非线性系统的稳定性问题，其中时滞是有界非光滑的，并且用线性矩阵不等式表示时滞.文献［6］进行了时滞下T－S模糊系统的鲁棒稳定性研究，结合分段时滞和增加状态向量建立新的Lyapunov－Krasovskii泛函，应用线性矩阵不等式的方法，得到保守性更小的时滞依赖稳定性参数.

2 研究问题描述

2.1 研究对象

考虑所研究的T－S模糊系统如下:

其中x(t)∈Rn为系统状态向量，z(t)∈Rp为待估计信号，u(t)是控制向量，Ai，Adi，Bi，Ci，Cdi，Di为具有适当维数的已知常数矩阵，r为模糊规则的数量，τ(t)为时滞，且0≤τm≤t(t)≤τM，μi(θ(t))满足:

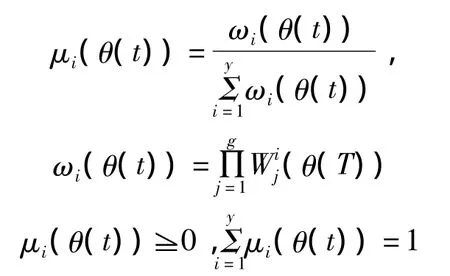
2.2 自适应事件触发机制描述

假设采样周期为h，相应的采样时刻记为tk，k∈R，传感器采样的向量为x(tk)，经过自适应事件触发机制输出的状态向量记为x(tk+j)，那么传感器采样的向量记为{x(t0)，x(t1)，…，x(tk)}，其中t0=0是初始释放时刻，k∈R.自适应事件触发器用来决定采样数据x(tk)是否释放到控制器中，释放时刻tk+j如下表示:

其中W=Rm×m是正定矩阵，δ(t)∈［0，1).nh是指当前采样时刻tk与下一个释放时刻tk+j之间的采样间隔.

类似文献［7－8］，考虑如下两个时段:

其中l是正实数，h是采样周期.

(1)若tk+h+d＞tk+1+dk+1，定义函数d(t)如下:

易得下面不等式:

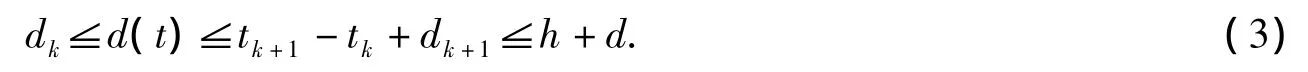
(2)若tk+h+d＜tk+1+dk+1，则存在正实数m使得

易得

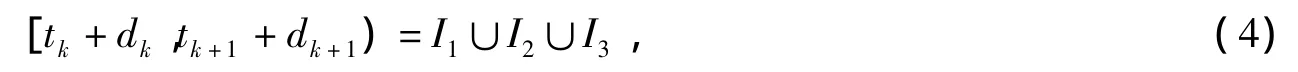
其中

由式子(3)和(4)定义函数d(t)如下:

由式子(5)定义的d(t)可以推出:

由式子(6)可以得到:

对t∈［tk+dk，tk+1+dk+1)定义ek(t)如下:

由式子(5)至(8)可以得到:

由式子(2)，(8)及(9)，自适应事件触发机制可以表示如下:

注1类似文献［9］，自适应事件触发机制中的触发参数δ(t)不是常数，而是动态变化的，它满足下面的微分方程:

其中δ(0)∈［0，1)是δ(t)的初始条件，d满足以下条件:

ρ是非负常数，注2将介绍ρ的寻找方法.

注2传输参数ρ的寻找方法如下

步骤1:对于给定的δM与τ1=0，设置τ2=τ2+μ，其中μ是τ2的单位增量，τ2是τ(t)的上界.

步骤2:对于步骤一中给定的τ2，如果存在满足线性矩阵不等式的解，进行步骤3;否则进行步骤1.

步骤3:基于定理2，用LMI工具箱寻找最大值τ2及相应的W.

步骤4:设定仿真时间T，基于事件触发机制［10］，取触发参数为δM，用Simulink找到每个采样时刻的状态误差ek(t).

2.3 控制器问题描述

本章要设置的状态反馈控制器描述如下:

其中，Kj∈Rm×n为待定的状态反馈增益矩阵.

注3控制器中接收的数据是经过自适应事件触发机制筛选的信号，即x(tk).

结合式子(1)、(9)及(13)，可以得到系统方程如下:

本章的主要目的是为T－S模糊系统(1)设计具有自适应事件触发机制的H∞控制器(13)，使得系统(14)指数均方随机稳定.

以下引理将在主要结果的证明中用到:

引理1［10］对给定的常数τM与矩阵R＞0，有下列不等式成立

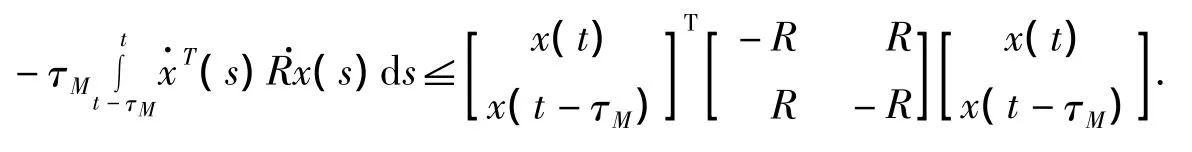
引理2［11］对任意的向量x，y∈Rn和正定矩阵Q∈Rn×n，下面不等式成立.

引理3［12］假设τ(t)满足0≤τm≤τ(t)≤τM，Ξ1，Ξ2和Ω是一些具有适当维数的已知常数矩阵，则

当且仅当(τM－τm)Ξ1+Ω＜0和(τM－τm)Ξ2+Ω＜0成立.

3 主要结果

在下面的主要结果中，定理1给出系统(14)指数均方随机稳定的充分性条件，定理2将给出(13)形式的自适应事件驱动下控制器的设计方法.

3.1 稳定性分析

定理1设参数τm≤τM，dM与δM为给定的正数，若存在对称矩阵P＞0，Qk＞0，Rk＞0(k=1，2，3)，W＞0及具有合适维数的矩阵Mij，Nij，Tij，Sij，使得以下矩阵不等式(15)成立，则基于自适应事件触发机制的T－S模糊系统(14)是渐近均方稳定的.

其中

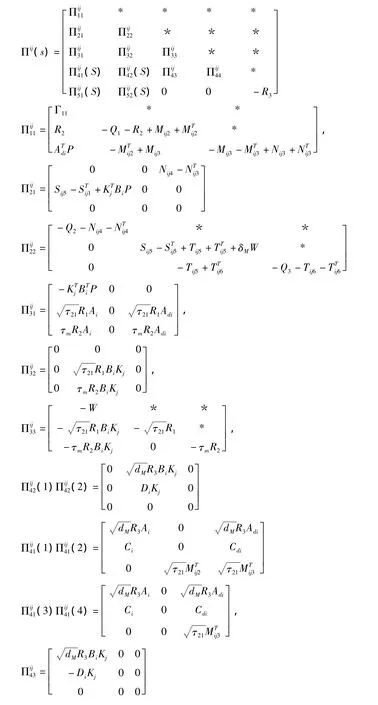
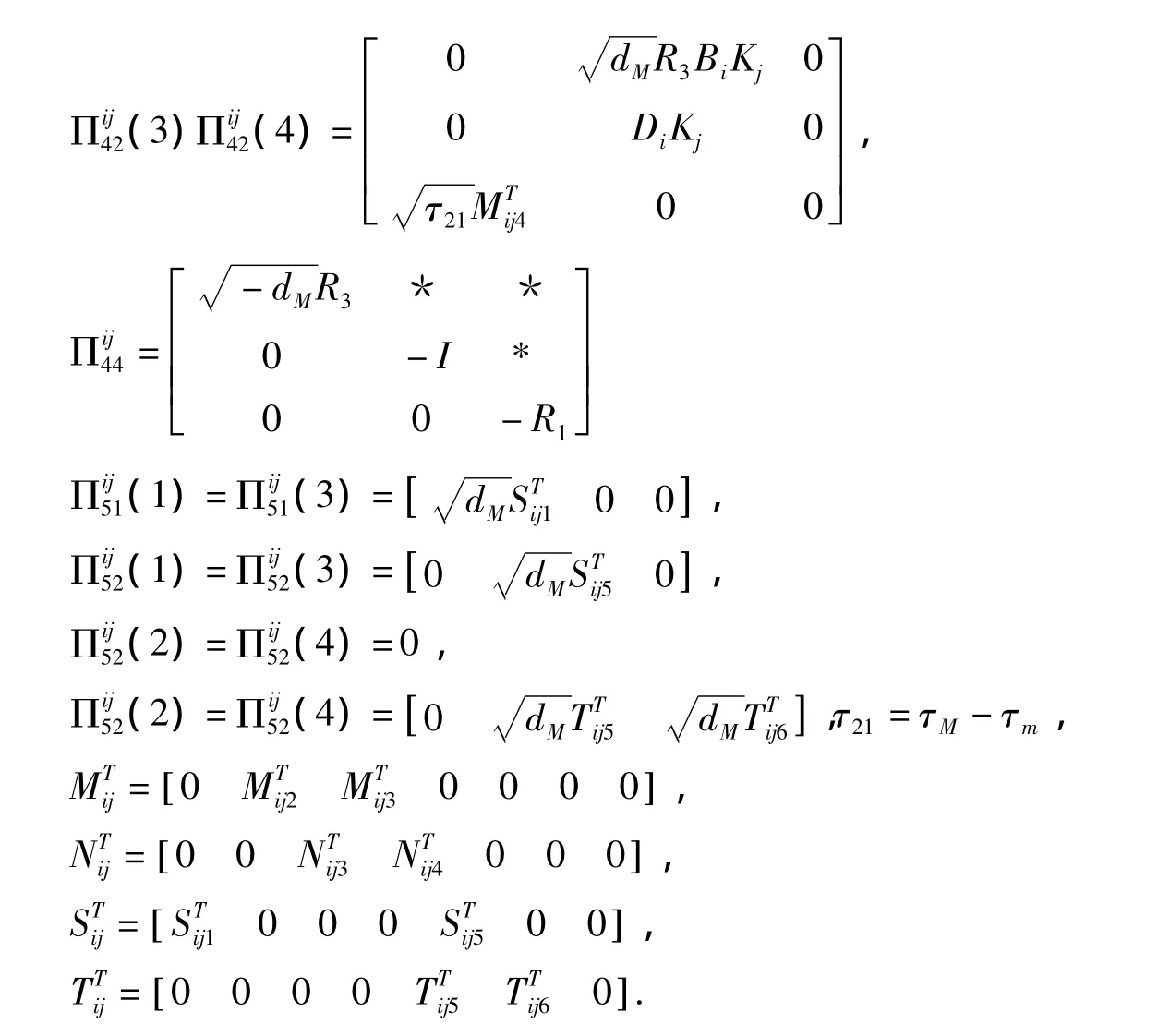
证明:构造如下Lyapunov－Krasovskii泛函:

其中

这里，P＞0，Qk＞0，Rk＞0(k=1，2，3)均为正定矩阵.

对V(t)求导得到:

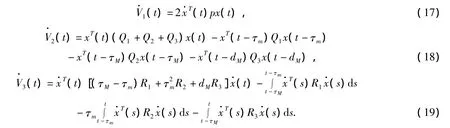
为接下来叙述方便，定义新的向量如下:

类似文献［10，14］，引入自由权矩阵Mij，Nij，Sij，Tij，用自由权矩阵方法可以得到:

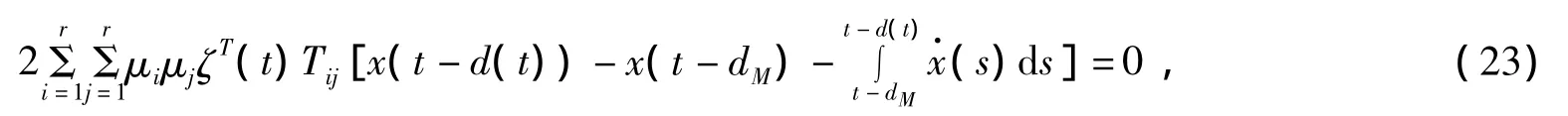
由式子(17)至(23)得到下面矩阵不等式:

应用引理1，可以得到:

应用引理2，可以得到:

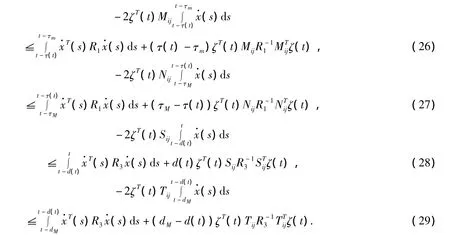
综合式子(24)至(29)可以得到(30)如下:

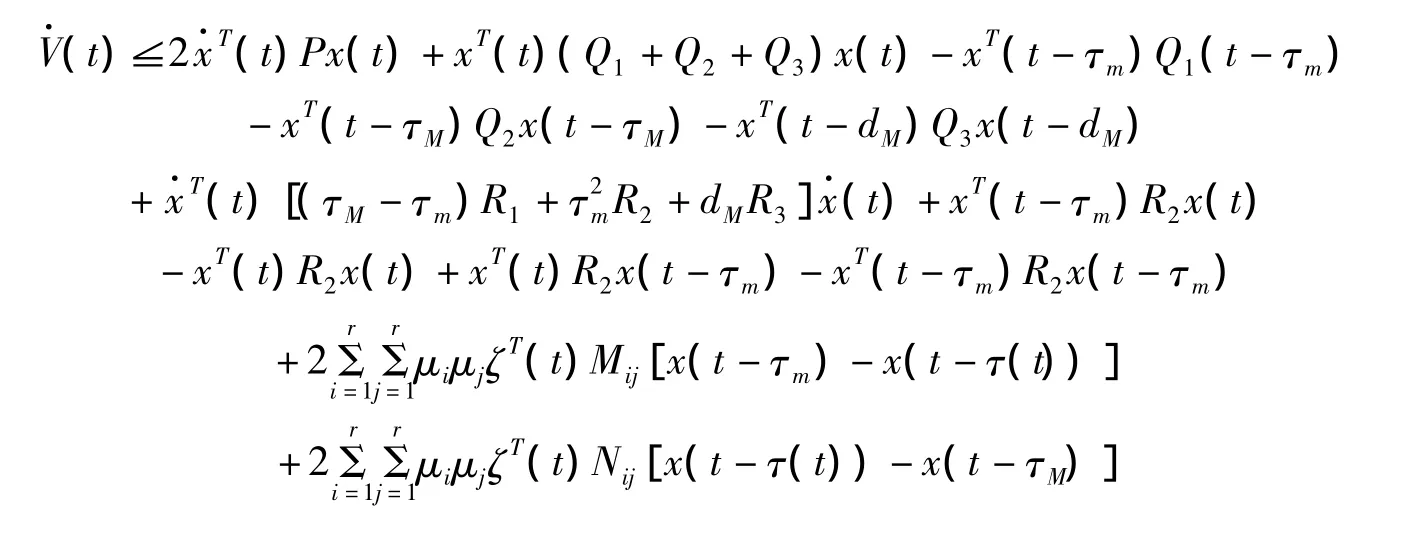
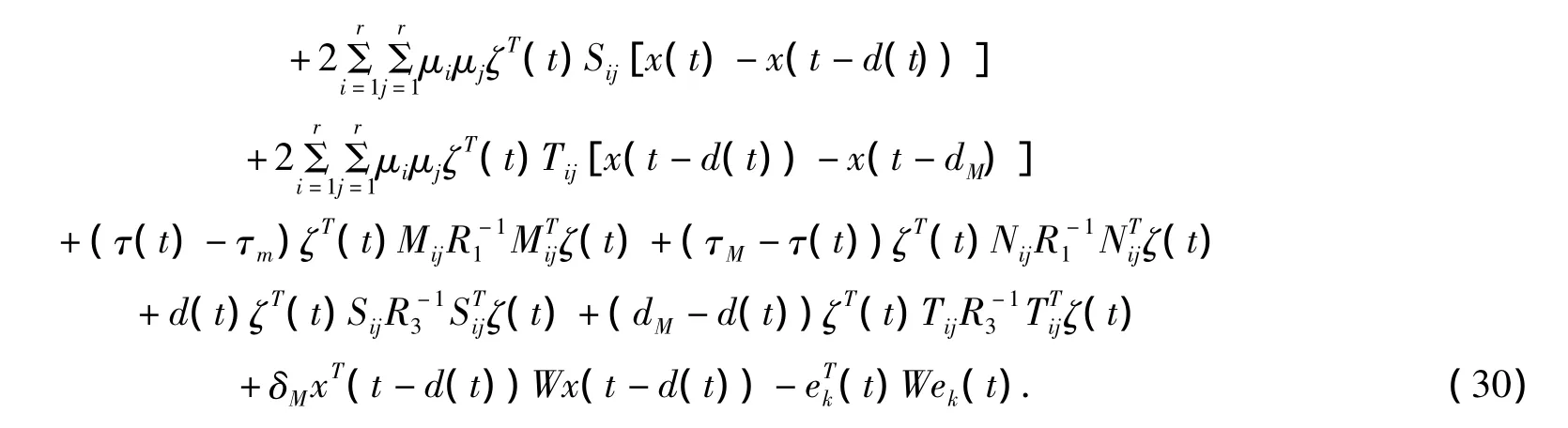
类似文献［15］，将引理3与引理4应用于(30)，容易得到(15)成立.由Lyapunov稳定性判定定理可知，模糊系统(1)是渐近稳定的.

3.2 自适应事件驱动下控制器设计方案

定理2设参数τm≤τM，dM，δM是给定的正数，若存在对称矩阵P＞0，k＞0(k=1，2，3)，k＞0(k =1，2，3)＞0及具有合适维数的矩阵，使得以下矩阵不等式(31)成立，则基于自适应事件触发机制的T－S模糊系统(14)是渐近均方稳定的.

其中

证明:根据引理4，矩阵不等式(15)成立，当且仅当下式成立:

其中

由于对任意的正定矩阵Rk，P，以及标量εk，由

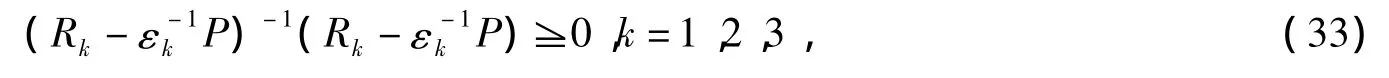
可以得到:

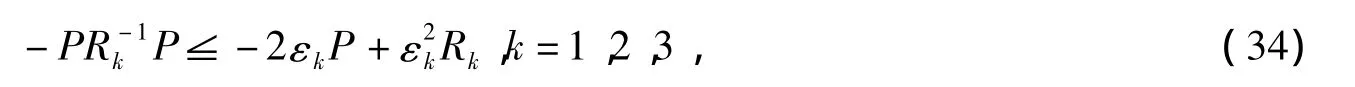
于是(35)为(32)成立的充分条件:

其中

4 仿真例子

下面将给出一个仿真例子来验证定理2的正确性，即提出的自适应事件驱动下控制器的设计方法是有效的.

例1考虑T－S模糊系统的参数如下:

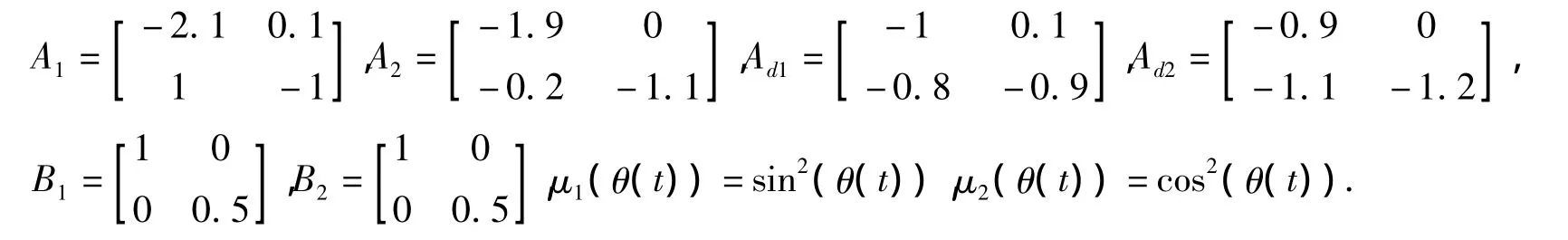
仿真中假设τm=0.1，τM=0.15，dM=0.3，δM=0.5，ε1=0.1，ε2=0.2，ε3=0.3，利用LMI工具箱求解定理2中的矩阵不等式，可以得到相应的触发矩阵W及增益K1和K2:

在Simulink中给定初始值x(0)=［－0.10.2］T，仿真时间为20s，采样周期h=0.08，图1表示x (t)的状态响应曲线，由图可得系统在T=8s处达到稳定状态;图2表示自适应事件触发机制下释放信号的时刻与间隔，这些经过筛选的点通过网络传入控制器，由于该机制中的δ(t)可以动态变化，所以选择的信号数量适中，既节省了网络资源，又保持了系统的控制性能.

根据ρ的求解机制，求得ρ=3.2591e－0.5，并得到参数d与触发参数δ(t)的仿真图，分别如图3与图4，可以观察出，当d=1时，δ(t)呈递增趋势;当d=－1时，δ(t)的值相应递减，这样事件触发机制得到自适应调节，保持了系统良好的控制性能.

图1 状态响应曲线

图2 触发信号的释放时刻与间隔

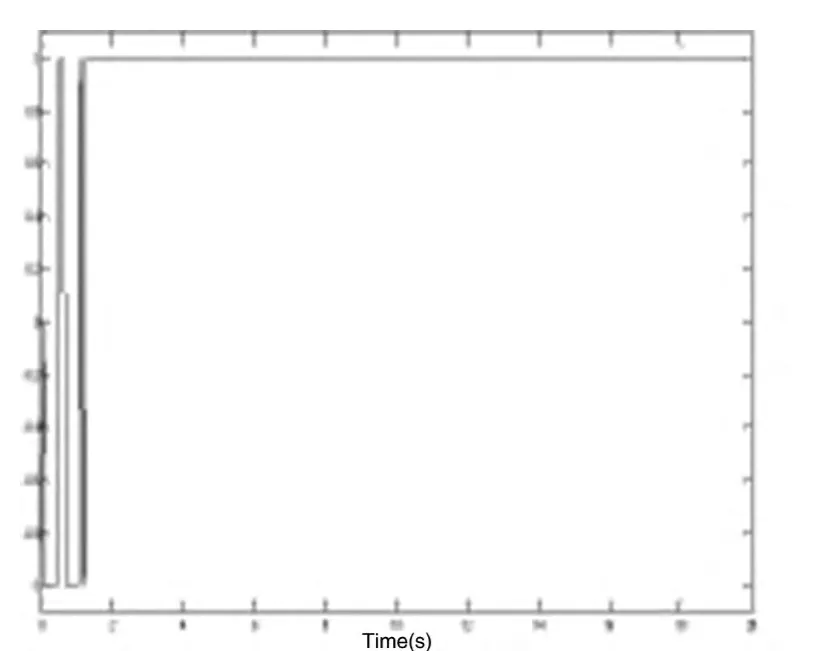
图3 参数d

图4 触发参数δ(t)

5 小结

本章设计了自适应事件驱动下T－S模糊系统的控制器.其主要特点是已经提出的自适应事件触发机制既有效的保持了系统的控制性能，又节省了网络有限的传输资源.在主要结果的证明中用到一种新的Lyapunov－Krasovski泛函和自由权矩阵，为求解线性矩阵不等式提供了方便，通过解线性矩阵不等式得到了控制器增益矩阵，最终仿真验证了设计方案的有效性.

［1］Wang H O，Tanaka K，Griffin M F.An approach to fuzzy control of nonlinear systems:stability and design issues［J］.IEEE Transactions on Fuzzy Systems，1996，4(1):14－23.

［2］陈珺.基于T－S模型的非线性系统模糊控制器设计及应用［D］.无锡:江南大学机械工程学院，2009.

［3］张果.基于T－S模型的非线性系统的模糊控制［D］.西安:西安电子科技大学数学与统计学院，2009.

［4］苏亚坤.基于T－S模糊模型的非线性系统的控制与滤波设计［D］.青岛:青岛大学数学与统计学院，2010.

［5］C.Lin，Q.Wang.Delay－dependent LMI conditions for stability and stabilization of T－S fuzzy systems with bounded time－delay［J］.Fuzzy Sets and Systems，2006，157(9):1229－1247.

［6］H.Zeng，Ju H.Park.Improved delay－dependent robust stabilization conditions of uncertain T－S fuzzy systems with time－varying delay［J］.Applied Mathematics and Computation，2014(235):492－501.

［7］S.Hu，D.Yue.Event－triggered control design of linear networked systems with quantizations［J］.ISA Transactions，2012(51):153－162.

［8］H.Li，C.Ming，S.Shen，et al.Event－triggered control for multi－agent systems with randomly occurring nonlinear dynamics and time－varying delay［J］.Journal of the Franclin Institute，2014(351):2582－2599.

［9］J.Zhang，C.Peng.An adaptive event－triggered communication scheme for networked control systems with randomly occurring nonlinearities and uncertainties［J］.Neurocomputing，2015(1):1－17.

［10］C.Peng，Y.C.Tian.Improved delay－dependent robust stabilization conditions of uncertainties fuzzy systems with time－varying delay［J］.Fuzzy Sets Systems，2008，159(20):2713－2729.

［11］C.S.Y.Wang，L.Xie.Robust control of a class of uncertain nonlinear systems［J］.System Control Letters，1992，19(2):139－149.

［12］D.Yue，E.Tian，Q.Han.A delay sytem method for designing event－triggered controllers of networked control systems［J］.IEEE Transactions Automatica Control，2013，58(2):475－481.

［13］俞立.鲁棒控制－线性矩阵不等式处理方法［M］.北京:清华大学出版社，2002.

［14］Y.He，M.Wu，J.She.Parameter－dependent Lyapunov functional for stability of time－delay systems with polytopic－type uncertainties［J］.IEEE Transactions Automatica Control，2004，49(5):828－832.

［15］D.Yue，Q.Han.Network－based Robust H∞filtering for uncertain linear systems［J］.Automatica，2006，54(11):4293－4301.

Adaptive Event－triggered Controller for T－S Fuzzy Systems

ZHANG Yuan－yuan
(School of Applied Mathematics，Nanjing University of Finance and Economics，Nanjing，210046，China)

Due to that Takagi－Sugeno(T－S)fuzzy model can approximate any continuous function by a series of the IF－THEN rules，so many traditional methods of linear system analysis are available for its research and it is one of the important tools of researching nonlinear uncertain systems.Therefore，NCSs have been widely investigated in T－S fuzzy model.In order to reduce the limited network resources，event－triggered scheme has been widely used in NCSs，which have important significance in theory.However，the current research about event－triggered scheme for T－S fuzzy system is not yet mature，how to design controller with adaptive event－triggered scheme is especially important.Based on event－triggered scheme，adaptive event－triggered scheme has been proposed，which is applied to the design of controller.Based on T－S fuzzy systems with time delay，an adaptive event－triggered controller is investigated.A general Lyapunov－Krasovskii functional and some slack matrices are used during the proof of main results.Schur complement lemma is used to deal with nonlinear matrix inequality，then by solving LMIs，the ideal controller are designed.Finally，the simulation verifies the validity of the proposed design.

adaptive event－triggered scheme;T－S fuzzy systems;controller;time－delay

TP13

A

1672－2590(2016)03－0073－13

2016－04－09

张媛媛(1989－)，女，河南鹤壁人，南京财经大学应用数学学院硕士研究生.