基于混沌序列稀疏化测量矩阵的ISAR成像*

谭歆　冯晓毅　王保平　程伟　方阳

(1.西北工业大学 电子信息学院, 陕西 西安 710129; 2.陕西科技大学 电气与信息工程学院, 陕西 西安 710021)



基于混沌序列稀疏化测量矩阵的ISAR成像*

谭歆1,2冯晓毅1王保平1程伟1方阳1

(1.西北工业大学 电子信息学院, 陕西 西安 710129; 2.陕西科技大学 电气与信息工程学院, 陕西 西安 710021)

摘要：在压缩感知逆合成孔径雷达(ISAR)成像中,构造测量矩阵是核心工作之一.混沌序列测量矩阵具有良好的伪随机性,能满足压缩测量的要求.针对混沌序列测量矩阵中非零随机元数目多而造成硬件实现困难的问题,文中提出了一种混沌序列稀疏化测量矩阵的构造方法.首先对混沌序列测量矩阵进行优化,然后沿矩阵对角方向进行置零稀疏化,最后将其应用于微波暗室进行ISAR成像实验.结果表明,与传统高斯随机矩阵成像方法相比,文中方法在降低计算复杂度、硬件实现难度基础上达到了ISAR成像的准确聚焦.

关键词：混沌序列;压缩感知;ISAR成像;微波暗室

近年来,基于压缩感知(CS)理论[1-3]进行逆合成孔径雷达(ISAR)成像成为雷达信号处理领域的一个研究热点[4].CS从理论上突破了传统Nyquist采样定理的限制,是基于信号的稀疏性、非相干测量及非线性优化重构方法来完成对信号的压缩采样与重构.压缩感知ISAR成像过程中,在给定成像场景和预设参数条件下,稀疏基的选取主要由ISAR回波自身信号模型决定,而设计构造低复杂度、易于硬件实现的测量矩阵对实现信号的压缩测量至关重要[5].目前多数文献中均选用高斯、伯努利等随机矩阵作为测量矩阵[6-7].这类随机矩阵固然普适性好,随机性强,能保证各列之间的低相干性,但由于独立随机元数目较多、数据存储空间较大、电路设计复杂而导致其硬件工程化难以实现.

混沌是非线性系统所独有且广泛存在的一种非周期运动形式.由于混沌系统所产生的序列具有初始值敏感、类随机、非周期和长期行为不可预测性的特点,因此有学者提出利用混沌序列进行CS测量矩阵的构造.Linh-Trung等[8]利用混沌序列构造出满足高斯随机分布的测量矩阵,重构效果甚至稍胜于一般随机测量矩阵.Yu等[9]利用混沌系统构造出混沌序列测量矩阵,并证明该矩阵满足RIP[10]性质,验证了该矩阵的可行性.郭静波等[11]构造的混沌循环测量矩阵很好地满足了RIPless特性,与传统的循环测量矩阵相比具有诸多的优越性.但上述混沌序列大多集中于改进输出序列的伪随机性,并未考虑重构过程的计算复杂度和物理电路实现难度的问题.因此,文中先对混沌序列测量矩阵进行优化,再沿矩阵对角方向进行稀疏置0,得到了混沌序列稀疏化测量矩阵,以减少测量矩阵中非零元数目,进而减少测量次数和降低计算复杂度,有效地缩短信号重构时间.最后将其应用于微波暗室进行压缩感知ISAR成像,以实现对ISAR回波信号的压缩测量,从而简化系统复杂程度,更好地节约硬件实现成本.

1压缩感知ISAR成像信号模型

在ISAR成像过程中,相对于雷达视线方向,目标运动可分解为平动分量和转动分量.由图1可知,平动分量对目标成像无贡献,所以首先进行平动补偿,转动分量则提供了方位向成像所必需的多普勒信息.假定目标进行平稳运动,在标准运动补偿后,可将目标模型转换为转台模型来处理.

图1　ISAR成像系统转台模型Fig.1　Model of turntable ISAR imaging system

ISAR回波信号经距离压缩和包络对齐处理后,得到rb处距离单元方位向全孔径回波信号模型:

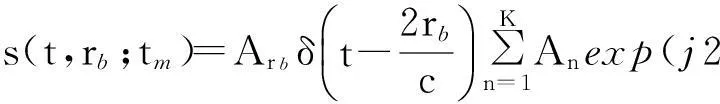
(1)

式中,rb为目标与雷达之间的距离,Arb为距离单元内脉压幅度,t为距离向快时间,tm为方位向慢时间,An和fn分别为距离单元内沿方位向第n个目标点的幅度和频率,ωtm为方位向噪声,K为距离单元内沿方位向目标点的个数[12].

对ISAR成像来说,由于方位相干积累时间内,方位孔径数据存在缺损或者丢失的现象比较严重,从而导致方位向分辨率下降,所以必须在保留可恢复有效信息的基础上,利用方位孔径缺损或者丢失的数据来完成对目标的高分辨成像.文中将方位向缺失孔径数据设置为0,则需要把存在孔径缺损的ISAR回波数据通过CS理论进行高精度重构.

根据ISAR回波信号的物理模型表达关系,可以构造相应的稀疏变化基Ψ,傅里叶基是ISAR成像最直观、最有效的基矩阵.Ψ具体表示为

(2)

式中:t0,t1,…,tN-1为方位向采样时刻；ω0,ω1,…,ωM-1为成像频率间隔.将稀疏基Ψ确定之后,设某一距离单元内存在方位孔径数据丢失或者缺损的ISAR回波信号为x,则α表示回波信号x在稀疏基Ψ下的稀疏向量,具体回波信号x可用式(3)来表示:

xN×1=ΨN×NαN×1

(3)

如图2所示,ISAR回波信号x经过测量矩阵Φ进行降维压缩测量后,得到观测信号y.

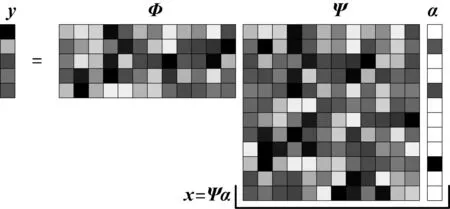
图2　压缩感知ISAR成像测量矩阵Fig.2　Measurement matrix of compressed sensing ISAR imaging

N维回波信号经过测量矩阵Φ降维压缩测量后得到M维观测信号的过程(其中M≪N)如下：

yM×1=ΦM×NxN×1=ΦM×NΨN×NαN×1

(4)

由于CS理论的目的在于根据低维观测向量y和测量矩阵Φ来重建高维原始信号x,而测量矩阵Φ是行少列多的矩阵,故从式(4)中求解出原始ISAR回波信号x就是欠定方程组的求逆问题,理论上有无穷多组解.但稀疏向量α是稀疏的,使得重构原始回波信号成为可能.因此附加了稀疏性这个先验条件及RIP性质约束才可能求出x的稳定唯一解,因此通过求解式(5)来获得唯一确定的解.

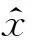
(5)

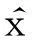
2混沌序列稀疏化测量矩阵的构造

压缩感知理论试图通过极少的数据来获取尽可能多的信息以精确恢复原始信号,因此测量矩阵的作用至关重要.虽然目前所普遍采用的高斯、伯努利等随机测量矩阵的重构结果比较好,但存在的不足也显而易见:在仿真试验中,测量矩阵的不确定性直接对实验结果的鲁棒性产生影响;而在实际工程应用中,还会造成计算复杂度高、存储空间大、硬件不易实现等问题.

混沌被认为是具有随机性行为的确定性动力系统中的现象.由于混沌序列自身良好的伪随机性特点,并且构造混沌序列测量矩阵的复杂度远远低于随机测量矩阵,所以其工程实现意义重大[13].

文中所构造的混沌序列稀疏化测量矩阵保留混沌序列测量矩阵[14]的伪随机性和易于构造的优秀特质,通过沿对角方向进行置0稀疏化[15-16],可以大幅减少测量矩阵中非0元素的数目,无疑降低了测量矩阵的构造复杂度和重构代价,势必节约了ISAR成像过程的实现成本.

混沌序列稀疏化测量矩阵的构造过程如下:

zk=xm+kd,k=0,1,2,…

(6)

如果混沌序列zk分布不满足均值为0和具有0对称特性,则需要进行零均值化和对称化处理.如果序列zk的分布为zk∈(0,1),则需要进行如下变换

zk=1-2zk,k=0,1,2,…

(7)

(2)由混沌序列zk作为混沌序列测量矩阵的基本元素,从zk序列中截断形成M×N维测量矩阵Φ′.为了确保测量矩阵列向量满足一定的线性独立性,可通过增大矩阵的奇异值来增强测量矩阵的线性独立性.因此,文中对测量矩阵进行近似QR分解,以实现对原有测量矩阵Φ′的优化.

(3)将完成近似QR分解优化改进后的测量矩阵进行按列归一化处理,即

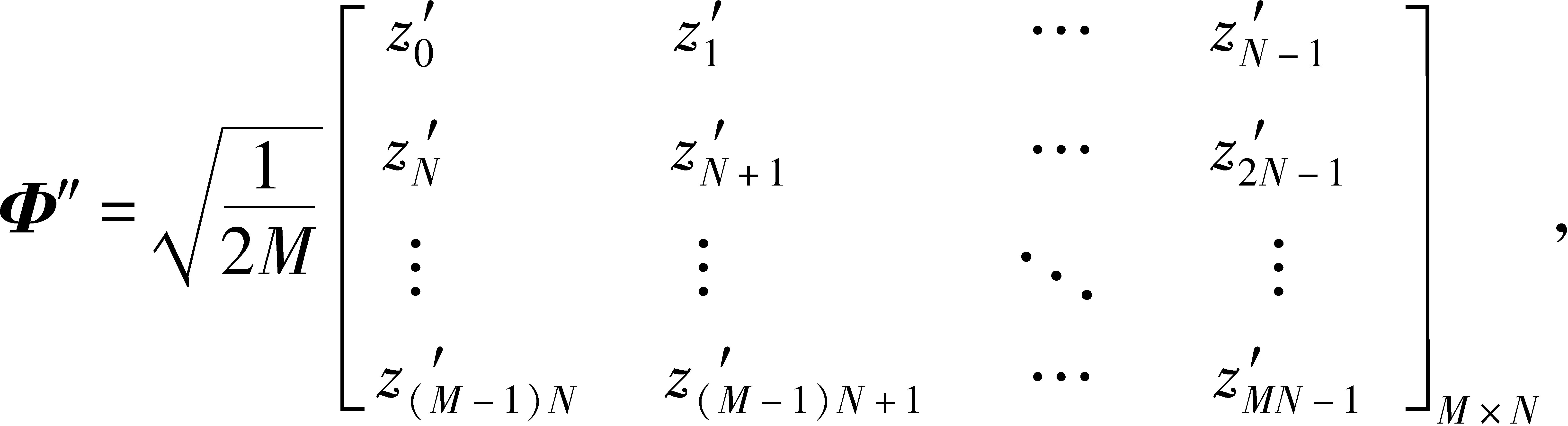
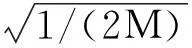
(4)对归一化之后的测量矩阵沿对角线方向进行置0稀疏化,得到最终的混沌序列稀疏化测量矩阵Φ,

文中根据以上算法步骤完成混沌序列稀疏化测量矩阵的构造,其中一维混沌序列采用Logistic、Tent映射,二维混沌序列采用Cat映射.

Logistic系统是目前应用最广泛的一类非线性动力学混沌系统.Logistic混沌映射的数学形式非常简单,其映射方程数学表达式为

xn+1=μxn(1-xn)

(8)

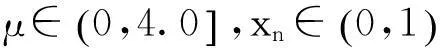
Tent混沌映射又被称为帐篷映射,其映射方程数学表达式为

(9)

式中,Tent系统参数μ∈(0,1),xn∈(0,1).当μ∈(0,1)变化时,系统处于混沌状态;当μ=0.5时,即为最典型的三角帐篷映射模型,三角帐篷映射结构简单,会呈现短周期现象,但Lyapunov指数和随机性等性能并不理想.

当利用再分段重构Tent映射时,文中构建改进的Tent序列表达式为

(10)

Cat映射是一种典型的二维离散混沌系统,其典型的映射方程数学表达式为

(11)

Cat映射方程每次迭代产生序列值舍去实数的整数部分,保留小数部分,得到二维混沌Cat序列,具有比一维更好的混沌分布特性.文中所构造的Logistic、Tent、Cat混沌序列测量矩阵参数如表1所示.

表1混沌序列测量矩阵参数

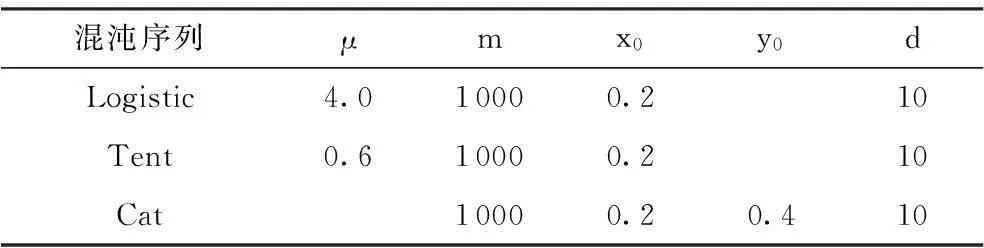
Table 1　Parameters of chaotic sequence measurement matrices

将构造的混沌序列测量矩阵按文中所提方法步骤及所设置参数进行重新构造,得到Logistic、Tent和Cat序列稀疏化测量矩阵.

3微波暗室数据实验与结果分析

为了验证文中所构造的混沌序列稀疏化测量矩阵进行ISAR成像的可行性和有效性,分别用高斯随机测量矩阵、Logistic序列稀疏化测量矩阵、Tent序列稀疏化测量矩阵以及Cat序列稀疏化测量矩阵进行4组暗室成像实验,利用微波暗室实测数据进行压缩感知ISAR成像,并对其成像质量进行比较.

微波暗室成像测试系统采用矩形暗室造型,其长25 m、纵深宽15 m、高15 m.雷达发出信号为步进频率信号,本次测试信号的工作频段为Ku波段,测试对象为5个金属目标球(直径是53 mm),放置于泡沫板中,如图3所示.图4为微波暗室内放置测试球的低散射泡沫转台支架.

图3　5个目标球Fig.3　Five target balls

图4　微波暗室泡沫转台支架Fig.4　Bracket of microwave anechoic chamber foam turntable

微波暗室成像测试系统所采用实验参数如下:载频fc=15 GHz,带宽B=6 GHz,步进频率Δf=5 MHz,方位角度范围为0°~5°,角度采样间隔Δθ=0.05°,小球直径Φ=53 mm.

在微波暗室测试中随机缺失50%的方位孔径数据,利用文中构造的混沌序列稀疏化测量矩阵进行压缩感知ISAR成像,结果如图5所示.

从图5(b)可以看出,在方位向的散焦比较严重.从图5(c)可知,在同样数据缺损条件下,利用高斯随机测量矩阵(测量数M=0.7N),采用OMP方法进行ISAR成像,聚焦效果明显.采用文中构造的Logistic序列稀疏化测量矩阵、Tent序列稀疏化测量矩阵及Cat序列稀疏化测量矩阵(非零元素数目仅占原矩阵元素的1/4)进行压缩感知ISAR成像,成像结果进一步精确聚焦.

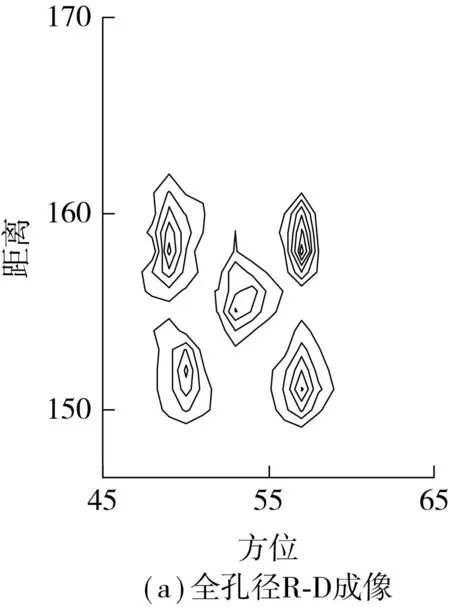
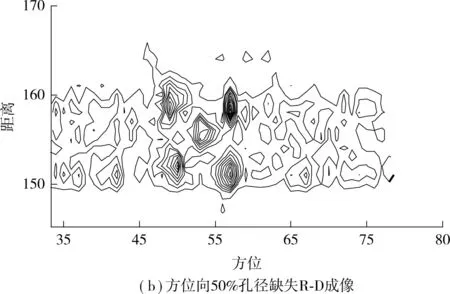
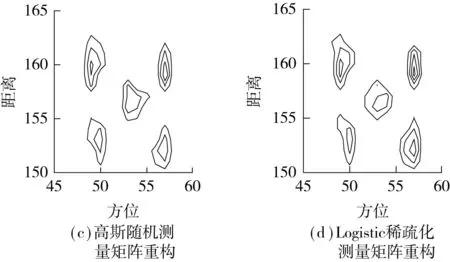
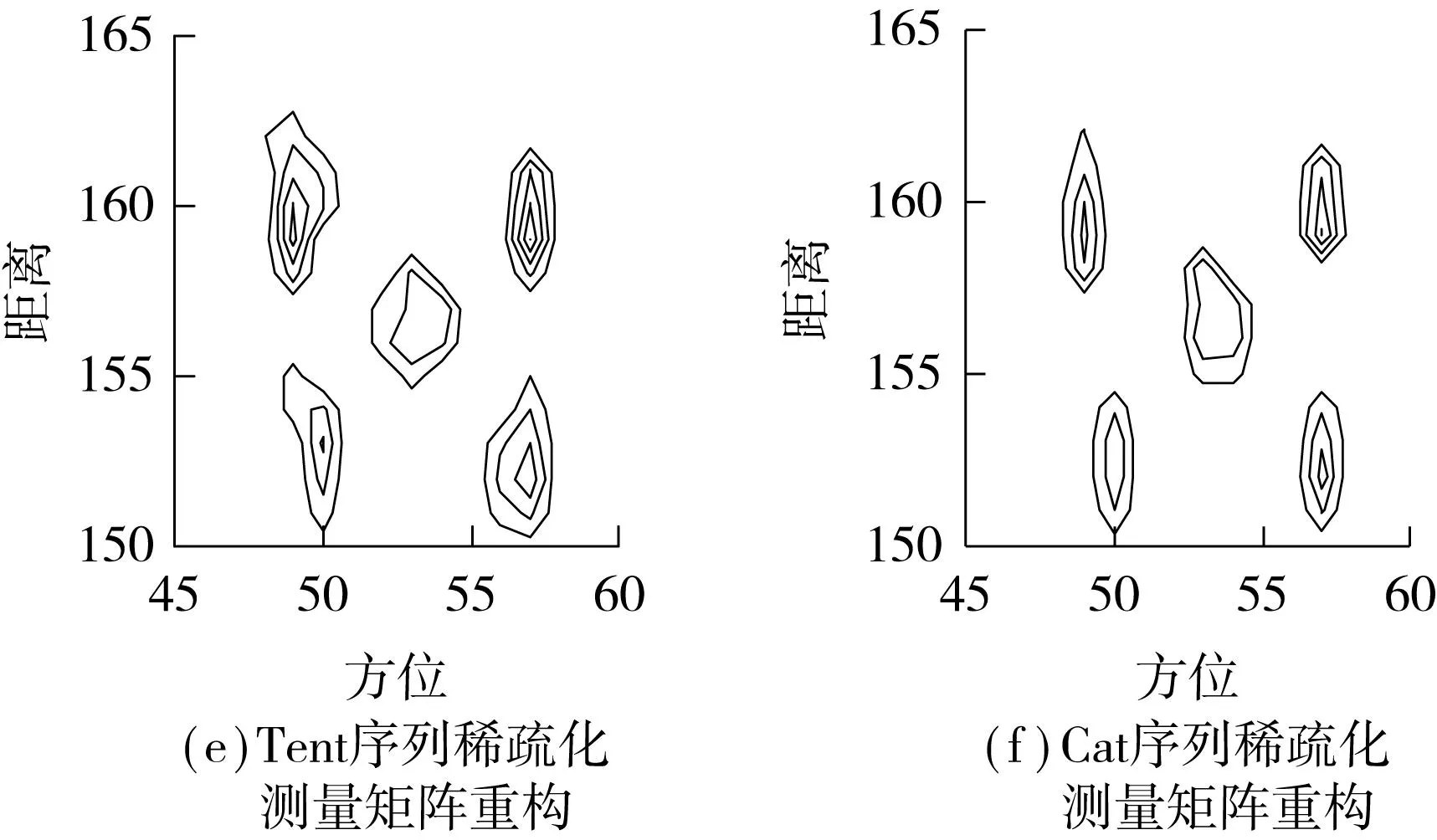
图5　基于稀疏化测量矩阵的微波暗室数据成像Fig.5　Microwave anechoic chamber data imaging based on sparse measurement matrices

为了定量分析评价文中所构造的混沌序列稀疏化测量矩阵对ISAR成像质量的影响,通过基于点目标模型的评价指标即峰值旁瓣比(PSLR)和积分旁瓣比(ISLR)来进行分析比较,结果如表2所示.

表2ISAR成像质量评价结果

Table 2Quality evaluation results for ISAR imaging dB

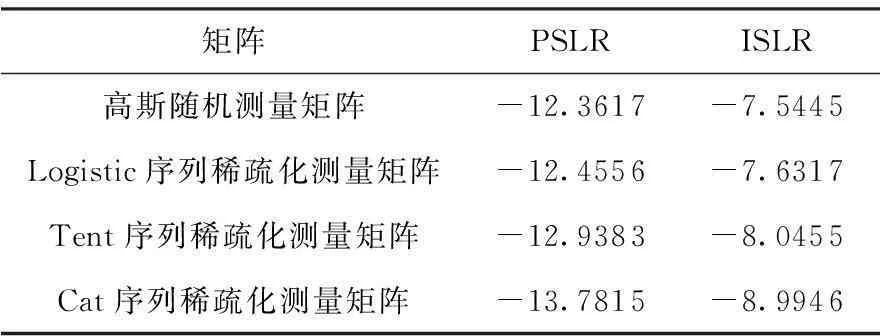
矩阵PSLRISLR高斯随机测量矩阵-12.3617-7.5445Logistic序列稀疏化测量矩阵-12.4556-7.6317Tent序列稀疏化测量矩阵-12.9383-8.0455Cat序列稀疏化测量矩阵-13.7815-8.9946

从图5和表2可以看出,经过稀疏化的混沌序列测量矩阵可大幅减少矩阵中的非0元素,降低硬件实现的难度,确保目标成像不受影响,在一定程度上提高聚焦效果.

为了说明和对比混沌序列稀疏化测量矩阵对成像结果的影响,采用图像的峰值信噪比(PSNR)准则对不同数量的ISAR回波信号的成像性能进行评价和比较,结果如图6所示.

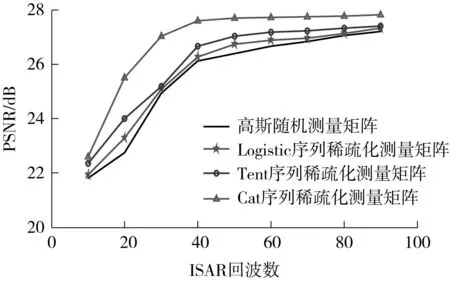
图6　不同混沌序列稀疏化测量矩阵的成像质量对比Fig.6　Comparison of imaging quality among different sparse chaotic sequence measurement matrices

从图6可知,对于不同数目的随机采样ISAR回波数据,混沌序列稀疏化测量矩阵的成像质量均优于高斯随机测量矩阵结果,并且二维混沌映射Cat序列稀疏化测量矩阵的结果明显优于一维映射Logistic及Tent序列的结果.

综合以上结果可知,混沌序列稀疏化测量矩阵由于非0元素数目显著降低,直接大幅降低测量矩阵构造的复杂程度.微波暗室数据实验结果表明,对不同的ISAR回波数据,混沌序列稀疏化测量矩阵的成像质量均优于高斯随机测量矩阵,并且高维混沌映射序列的聚焦效果及成像质量明显优于低维混沌映射序列.

4结论

文中提出了一种混沌序列稀疏化测量矩阵的构造方法,并应用于压缩感知ISAR成像.该方法保留了混沌序列自身内在确定性与外在随机性相统一的优点,稀疏化过程克服了独立随机元数目过多、信号重构过程运算复杂、物理电路不易实现的缺点,具有工程化的潜在优势.微波暗室实验验证该方法的重构稳定性更好,聚焦准确性更高,具有一定的实用意义和价值.从实际测试角度进行矩阵优化改进,或者探讨超混沌测量矩阵构造算法将是今后进一步研究的方向.

参考文献:

[1]DONOHO D L.Compressed sensing [J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.

[2]CANDES E J,ROMBERG J,TAO T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information [J].IEEE Transactions on Information Theory,2006,52(2):489-509．

[3]BARANIUK R.A lecture on compressive sensing [J].IEEE Signal Processing Magazine,2007,24(4):118-121.

[4]ENDER J H G.On compressive sensing applied to radar [J].Signal Processing,2010,90(5):1402-1414.

[5]张劲东,张弓,潘汇,等.基于滤波器结构的压缩感知雷达感知矩阵优化 [J].航空学报,2013,34(4):866-868．

ZHANG Jin-dong,ZHANG Gong,PAN Hui,et al.Optimized sensing matrix design of filter structure based compressed sensing radar [J].Acta Aeronautica et Astronautica Sinica,2013,34(4):866-868.

[6]CANDES E J,ROMBERG J K,TAO T.Stable signal recovery from incomplete and inaccurate measurements [J].Communications on Pure and Applied Mathematics,2006,59(8):1207-1223.

[7]CANDES E J,TAO T.Decoding by linear programming [J].IEEE Transactions on Information Theory,2005,51(12):4203- 4215.

[8]LINH-TRUNG N,VAN PHONG D,HUSSAIN Z M,et al.Compressed sensing using chaos filters [C]∥Procee-dings of Telecommunication Networks and Applications Conference.Adelaide:IEEE,2008:219-223.

[9]YU L,BARBOT J P,ZHENGG,et al.Compressive sen-sing with chaotic sequence [J].IEEE Signal Processing Letters,2010,17(8):731-734.

[10]HAUPT J,NOWAK R.A generalized restricted isometry property [R].Madison:Department of Electrical and Computer Engineering,University of Wisconsin-Madison,2007.

[11]郭静波,汪韧.基于混沌序列和RIPless理论的循环压缩测量矩阵的构造 [J].物理学报,2014,63(19):198402.

GUO Jing-bo,WANG Ren.Construction of a circulant compressive measurement matrix based on chaotic sequence and RIPless theory [J].Acta Physica Sinica,2014,63(19):198402.

[12]李军,邢孟道,张磊,等.一种高分辨的稀疏孔径ISAR成像方法 [J].西安电子科技大学学报,2010,37(3):441- 446.

LI Jun,XING Meng-dao,ZHANG Lei,et al.High resolution imaging method for the sparse aperture of ISAR [J].Journal of Xidian University(Natural Science),2010,37(3):441- 446.

[13]KAFEDZISKI V,STOJANOVSKI T.Compressive sampling with chaotic dynamical systems [C]∥Proceedings of the 19th Telecommunications Forum.Belgrade:IEEE,2011:695- 698.

[14]PENG Z N,ZHANG G,ZHANG J D,et al.Optimized measurement matrix design using spatiotemporal chaos for CS-MIMO radar [J].Mathematical Problems in Engineering,2014,42(4):1-8.

[15]HAUPT J,BAJWA W U,RAZ G,et al.Teoplitz compressed sensing matrices with applications to sparse channel estimation [J].IEEE Transactions on Information Theory,2011,56(11):5862-5878.

[16]张成,杨海蓉,韦穗.基于随机间距稀疏Toeplitz测量矩阵的压缩传感 [J].自动化学报,2012,38(8):1362-1369.

ZHANG Cheng,YANG Hai-rong,WEI Sui.Compressive sensing based on deterministic sparse Toeplitz measurement matrices with random pitch [J].Acta Automatica Sinica,2012,38(8):1362-1369.

ISAR Imaging Based on Sparse Chaotic Sequence Measurement Matrices

TANXin1，2FENGXiao-yi1WANGBao-ping1CHENGWei1FANGYang1

(1. School of Electronics and Information, Northwestern Polytechnical University, Xi’an 710129, Shaanxi, China;

2. School of Electrical and Information Engineering, Shaanxi University of Science and Technology, Xi’an 710021, Shaanxi, China)

Abstract:The construction of measurement matrices is one of the core tasks in compressed sensing inverse synthe-tic aperture radar (ISAR) imaging. The chaotic sequence measurement matrices are of excellent pseudo-randomness, which can meet the requirements of compressive measurement. As it is difficult to implement the hardware engineering of the chaotic sequence measurement matrices because of the huge number of independent random elements, a construction method of sparse chaotic sequence measurement matrices is proposed in this paper. In the method, the chaotic sequence measurement matrices are optimized, and then setting the zero along the diagonal direction is performed to make the matrix sparse. Finally, the sparse chaotic sequence measurement matrices are used to conduct ISAR imaging experiments in a microwave anechoic chamber. The results show that, in comparison with the Gauss random matrix imaging method, the proposed method achieves an accurate focusing of ISAR imaging and reduces the computational complexity and the hardware implementation difficulty.

Key words:chaotic sequence; compressed sensing; ISAR imaging; microwave anechoic chamber

doi：10.3969/j.issn.1000-565X.2016.01.010

中图分类号：TN957

作者简介：谭歆(1978-),男,博士生,主要从事微波雷达成像、压缩感知雷达信号处理研究.E-mail:tanxin999@sina.com

*基金项目：国家自然科学基金资助项目(61472324);国家自然科学基金青年科学基金资助项目(61401360);西北工业大学中央高校基本科研业务费专项资金资助项目(3102014JCQ01055)

收稿日期：2015-06-05

文章编号：1000-565X(2016)01- 0065- 06

Foundation items： Supported by the National Natural Science Foundation of China(61472324) and the National Natural Science Foundation for Young Scientists of China(61401360)