非对称双栅结构a-Si:H薄膜晶体管沟道电势统一模型*

秦剑　姚若河

(华南理工大学 电子与信息学院, 广东 广州 510640)



非对称双栅结构a-Si:H薄膜晶体管沟道电势统一模型*

秦剑姚若河†

(华南理工大学 电子与信息学院, 广东 广州 510640)

摘要：针对非对称双栅结构的非晶硅薄膜晶体管,根据高斯定理建立了表面势与背电势随栅压变化的隐含关联方程组,通过求解一维泊松方程推导了前、背栅压独立偏置条件下统一的沟道电势模型.该模型所需参数可由实验直接提取,数值拟合量少,在特定条件下可简化为对称双栅模型.在此基础上,文中利用数学变换及Lambert W函数提出了表面势与栅压隐含方程的近似求解方法.数值模拟结果显示,该方法具有良好的数值收敛特性,可直接用于器件仿真软件的初值设定,有效提升了模型自洽解的运算效率.

关键词：非对称双栅薄膜晶体管;表面势;氢化非晶硅;陷阱态;近似解

相对单栅而言,双栅结构的非晶态薄膜晶体管(TFT)由于场效应迁移率高、亚阈特性好、驱动能力强等优点而受到业界的重视,已广泛应用于大面积有源矩阵液晶面板、有源矩阵式有机发光二极管显示器(AMOLED)等领域[1-2].建立独立偏置条件下完整的沟道电势模型对研究不同沟道界面特性、量化有源层内电场分布及构建器件相关紧致物理模型具有重要的意义.Baudrand等[3]最早利用有限元差分方法对双栅结构的薄膜晶体管沟道电势进行求解,但计算量大使其应用受到一定的限制,较少用于器件的电路仿真与设计.Young[4]提出的模型为描述类似结构的绝缘层上硅(SOI)器件短沟效应及准二维阈值电压模型的建立提供了有效途径,但该模型建立在全耗尽近似的基础上,并不适用于本征或轻掺杂特性的非晶类半导体器件.此外,a-Si:H中存在的大量随能级变化的复杂陷阱态密度也为建模带来了困难.在前、背栅压及栅绝缘层厚度完全相等的前提下,文献[5]给出了对称双栅结构a-Si:H TFT(sDG a-Si:H TFT)表面势与中点电势的准解析模型,有效提升了模型自洽解的运算效率.然而,近年来随着双栅TFT器件结构的不断优化,前、背栅绝缘层介电系数与厚度并不严格相等,在双栅相互独立的偏置模式下(Vgf≠Vgb),上述对称特性将被打破,由此得到的电势模型将不再适用.

从目前的文献来看,双栅TFT非对称特性研究局限于不同绝缘栅厚度或界面材料对器件电学特性的影响[6-8],独立栅压交互影响下沟道电势与薄膜厚度及陷阱态密度之间的量化关系尚不明确,完备的沟道电势模型亦未见报道.此外,现有模型大多假设有源层厚度无限厚以忽略体内电势与电场的连续变化,并不适用于预测具有更薄有源层厚度的电势变化及其对器件电学特性的影响.

针对以上问题,文中运用等效特征温度近似方法[5]对前序工作进行扩展.首先运用高斯定理建立了沟道电势随栅压变化的隐含关联方程组；然后应用图解法及LambertW函数给出隐含方程中表面势与背电势的近似求解方法,推导得到了独立偏置条件下统一的沟道电势模型；最后通过二维器件仿真软件验证该模型的有效性,并对该模型嵌入仿真器后的运算效率进行了估算.

1物理模型及求解

首先建立非对称双栅a-Si:H TFT(aDG a-Si:H TFT)器件的结构模型,如图1所示,其中Y轴为沟道电流方向,X轴为垂直于沟道的纵向电场方向,tSi、toxf及toxb分别为器件的有源层及前、后背栅厚度.与传统反交叠单栅结构的a-Si:H TFT不同[9],双栅结构的a-Si:H TFT在源、漏电极淀积成型后,还需继续淀积一层Si:Nx绝缘层,第2栅极(前栅)以对应第1栅极(背栅)的方式形成于源、漏电极之上.文中重点研究前、背栅绝缘层厚度不相等且驱动模式相互独立的情况下表面势与背点电势随偏置变化的一般规律,并做如下假设[10-11]:①基于一维的缓变沟道近似(GCA)成立,即∂φ/∂x≫∂φ/∂y;②a-Si:H硅膜为本征/轻掺杂N型半导体材料且有源层厚度大于10 nm,忽略由超薄沟道引发的量子效应的影响.

当考虑受主深能态与带尾态两部分时,a-Si:H陷阱态密度分布函数呈现双指数特性[12],即

(1)

式中,E为陷阱态能级,gd、gt分别为深能态和带尾态在导带边界处的有效态密度,Td、Tt分别为深能态和带尾态的特征温度,k为玻尔兹曼常数,EC为导带能级.a-Si:H薄膜的陷阱态荷电密度表示为

(2)

式中,EV为价带能级, f(E)为费米-狄拉克分布(F-D)函数.自由电子浓度表示为

(3)

式中,Efn为电子准费米能级,T为当前温度.综合考虑自由载流子与陷阱态密度的影响,在垂直于沟道的X轴方向上构建一维泊松方程,可得

(4)

式中,φ为电势,q为元电荷电量,εSi为a-Si:H的介电常数.为了更好地研究不同偏置条件下表面势与背电势的变化规律,文中引入等效特征温度近似方法[13],结合式(1)-(4)可得

(5)

式中,TE、Neff分别为等效特征温度及界面处等效荷电量密度,φch为沟道电势,EFO为体费米能级.

Neff在不同偏置范围内由下列分段函数给出,即

(6)

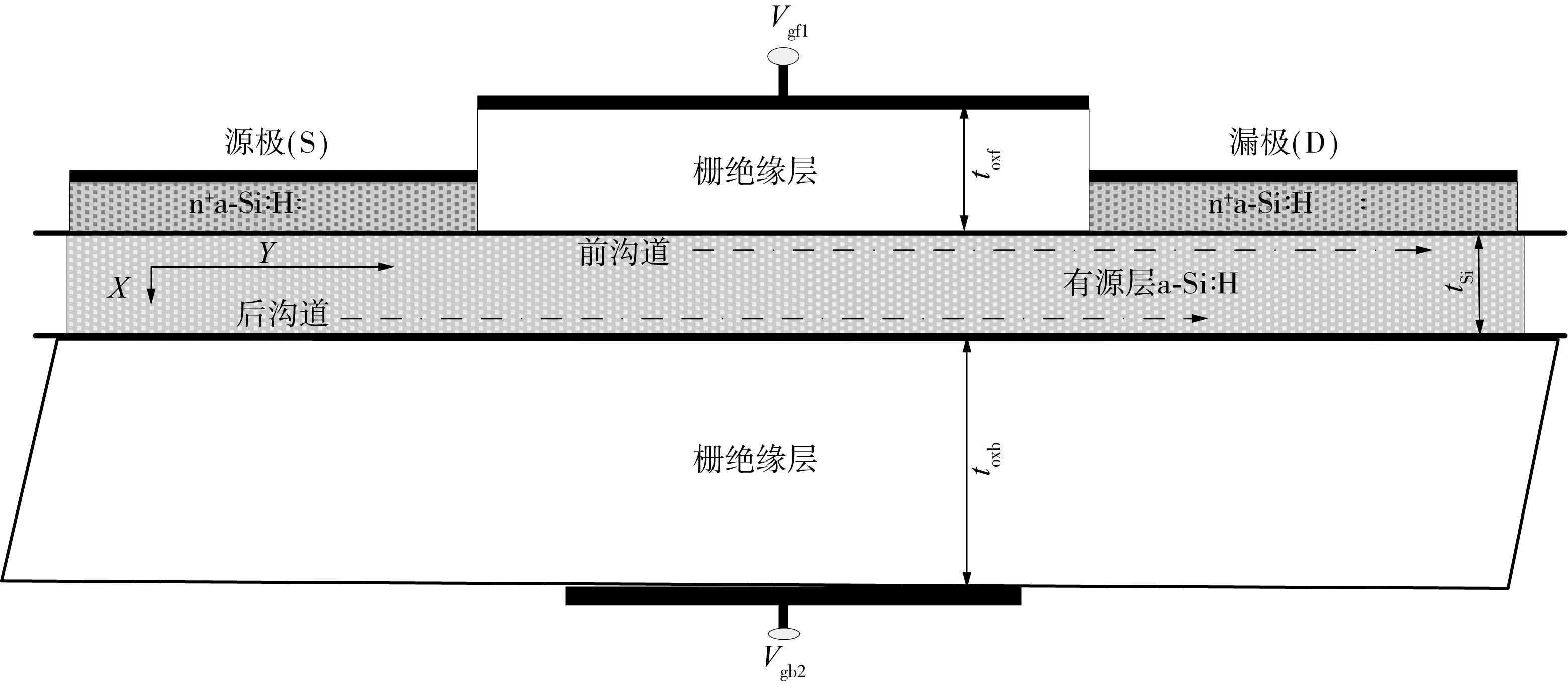
图1　非对称氢化非晶硅双栅薄膜晶体管的剖面结构示意图Fig.1　Schematic diagram of asymetrical a-Si:H dual gate TFT cross section

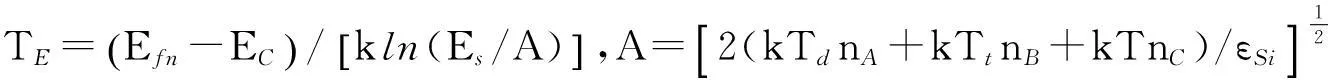
(7)

式中,C1为积分引入的常数项,作为前-背栅独立偏置条件下交互耦合的参数特性.与对称双栅结构不同,对于驱动状态相互独立的非对称双栅a-Si:HTFT而言,存在下列一般化的边界条件,即

φ(0)=φs

(8)

φ(tSi)=φb

(9)

文中定义顶部绝缘层与有源层界面处的电势为表面势φs,底部绝缘层与有源层界面处为背电势φb,设绝大部分栅压降落于栅绝缘层Si:Nx/a-Si:H界面处,应用高斯定理有

εSiF(0)=(εoxf/toxf)[φs-(Vgf-VFBf)]

(10)

εSiF(tSi)=-(εoxb/toxb)[φb-(Vgb-VFBb)]

(11)

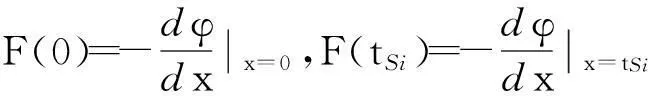
(12)

H=2kTENeff/εSi

(13)

(14)

(15)

因此,前栅与背栅电势值可由下列相互关联方程组决定:

(16)

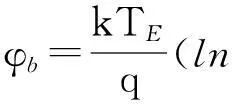
(17)

将式(16)代入式(17),整理展开可得

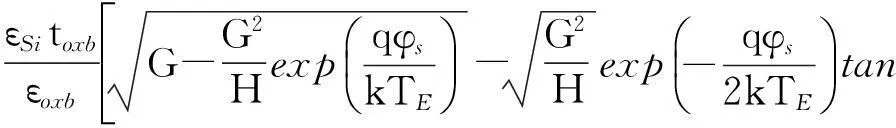
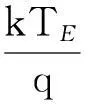
(Vg2-VFBb)=0

(18)

注意到式(18)为一个仅包含表面势φs且与背栅偏压Vgb2直接关联的隐含方程,形式十分复杂,无法直接获得对应的解析解,进一步求解该方程必须借助Newton-Raphson(NR)迭代算法,此外还需提供物理意义明确的方程初始解.这将消耗大量的计算资源,同时无法保证解的收敛性.为此,文中给出了一种新方法来对上述关联方程组进行近似求解.

以前栅为参考点,即在x=0处,由式(7)有

(19)

将式(19)代入式(10),整理可得

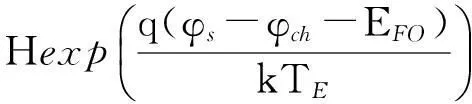
(20)

在x=tSi处背栅有类似的等式成立.容易看出,式(19)中引入的参数C1综合体现了前-背栅压相互耦合的关联特性,与式(14)(参数G)的本质是一致的,但数值上相差一个关联系数H,即C1=G/H,其中H由式(13)给出.令G′=-HC1,文中借助图解法分析式(20)等号两侧的参变量,如图2所示.图中曲线LHS表示式(20)等号左侧的平方项,曲线RHS为右侧G′与指数项的和,交点处为不同栅偏压环境下方程的解.图2表明,随着前栅偏压由小到大逐渐增加,方程的解主要由RHS指数项部分主导,而与耦合变量G′的相关性渐渐降低.特别地,当G′=0时,背栅压影响消失,自由载流子仅在前栅绝缘层与硅膜界面处非常薄的位置处积累,体电势与电场的变化被合理忽略,式(20)简化为单栅结构的a-Si:HTFT形式[14].

图2　式(20)各部分图形化求解示意图Fig.2　Schematic diagram of graphical solution for each part of Eq.(20)

进一步观察式(20),令z=(G/H)exp(-qφs/(kTE)).应用LambertW函数[10],则存在表面势隐含方程:

φs(z)=(Vgf-VFBf)-2kTE/q·

结合上述分析,令z=0,有

(21)

式(21)可视为表面势随前栅压变化的近似解析解,借助式(17)可获得关联电势φb的数值解.此外,对于对称型双栅结构的a-Si:HTFT,由于前、背栅电压大小及绝缘层厚度完全相等,即Vgf=Vbf,toxf=toxb,电势在接近有源层中点位置的梯度变化接近为0,电场反向变化.运用特定的边界条件:φ(0)=φ(tSi)=φs,φ(tSi/2)=φo,φ′(tSi/2)=0,关联方程组(16)、(17)可简化为

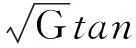
(22)

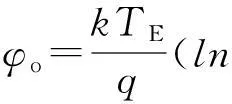
(23)

(24)

注意到式(22)成立的充分条件为γ=0,则表面势由下列等式决定:

(25)

式中,θ由式(15)给出.尽管式(25)也需要迭代求解,但与非对称情形下隐含方程(18)相比已大为简化.作为上述情形的特例,文献[5]使用分区方法给出了上述方程组的近似解析解.

下面利用已获得的表面势与背电势数值解进一步分析非对称双栅结构对器件阈值电压的调制影响.以背栅Vgb2恒定偏置于阈值电压附近为例,分析前栅Vgf1对阈值电压的影响.综合考虑双栅界面(a-Si:H/Si:Nx)电场及有源层内电场项,有

εoxbF(tSi)-εSiFs=-Ctbφb

(26)

εoxfF(0)-εSiFs=Ctfφs

(27)

式中,Fs为有源层体内有效电场,F(0)、F(tSi)分别由式(10)及式(11)给出,Ctb、Ctf为考虑陷阱态密度的等效电容,与式(6)给出的等效陷阱态密度相关.当背栅偏置较小时,器件工作在弱积累态,载流子在界面处的一维变化梯度(x轴)远超体内,近似存在φs-φb=Fs/tSi,进一步联立式(10)、(11)、(26)、(27),有

(28)

式中,Coxf=εoxf/toxf,Coxb=εoxb/toxb,Cs=εSi/tSi.反之有类似的结论.式(28)表明,非对称双栅TFT结构中顶栅与低栅对器件阈值电压的调制影响并不相同,平移阈值量主要与绝缘层介电常数及相对厚度比值、有源层厚度及陷阱态密度相关.对于典型的非对称双栅结构a-Si:HTFT,式(28)等号右边的值在0.16~0.18之间,与具体的器件尺寸及制备工艺相关,此预测与文献[15]提取的实验数据是近似一致的.

2实验结果及讨论

为验证文中模型的有效性,基于二维半导体器件仿真软件MEDICI对上述物理模型进行模拟.其中a-DGa-Si:HTFT器件结构如图1所示,有源层网格设置(MESH)及相关物理模型调用与文献[16]一致.模型建立在前、背栅压独立偏置条件下非对称器件结构的基础上,即Vg1≠Vg2,toxf≠toxb.a-Si:H局域陷阱态密度及相关物理参数提取方法见文献[17],具体参数设置如下:gt=2.1×1022cm-3eV-1,gd=8.68×1018cm-3eV-1,Td=997K,Tt=285K,Nc=1.05×1019cm-3,ε0=8.85×10-14F/cm,εSi=1.05×10-12F/cm,εoxf=εoxb=5.75×10-13F/cm.

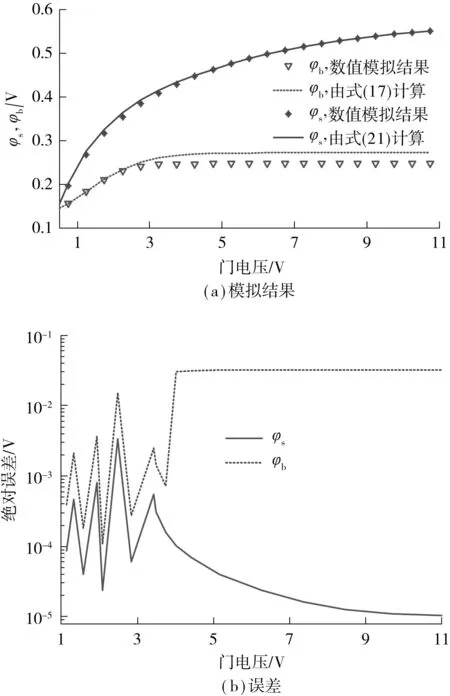
图3　φs及φb的模型近似解与数值模拟结果对比Fig.3　Comparison of φsand φb between the approximate solu-tion by the model and the numerical simulation results

设计如下模型进行测试实验:a-DG a-Si:H TFT器件尺寸toxf=250 nm,toxb=400 nm,tSi=60 nm;偏置满足背栅压Vgb=0 V,漏电压Vds=0 V;前栅压Vg1从0 V扫描至11 V,离散间隔为0.25 V,分别求解表面势φs与背电势φb.MEDICI数值模拟结果与模型近似求解结果绘于图3.其中表面势近似解φs由式(21)给出,背电势φb由关联等式(17)给出.图3表明,模型给出的表面势近似解与数值模拟结果十分接近,两者的绝对误差项随栅压的增加快速下降至10-5左右的数量级,显示了模型的有效性.主要误差项源自等效特征温度在从亚阈到开启区过渡过程中引发的计算误差.此外,由于背栅压Vgb恒定,背电势φb被钳制在某一固定数值范围内,基本上不受前栅压变化的影响,这与式(17)的预测结果相一致,文献[7]从实验的角度给出了类似的结论.特别指出,模型中除体费米能级EFO、前/后栅平带电压VFBf及VFBb需数值拟合外,其余参数均可从a-Si:H 硅膜中由相关物理实验直接提取,具有明确的物理意义,并非数值拟合量.

为了进一步估算模型嵌入AIM-SPICE中的运行速度,在一台双核Pentium IV + 4 GB内存PC机、Maple环境下基于NR迭代思路将上述实验循环1 000次,采用不同方法对隐含关联方程(16)、(17)进行数值求解,收敛条件为误差数值项低于10-11.测试结果见表1.表1表明,给定偏置条件下,两种方法均能使表面势有效收敛,但因受到随机初始解等因素的影响,文中方法完成一次循环所需计算时间比文献[18]中二阶NR方法平均减少65.7%,单个偏置节点对背电势的解算具有类似的特性.由此可见,文中方法收敛速度更为迅速,有效降低了模型自洽解的求解时间,十分适合于器件的电路设计与仿真分析.

表1两种方法的测试结果比较

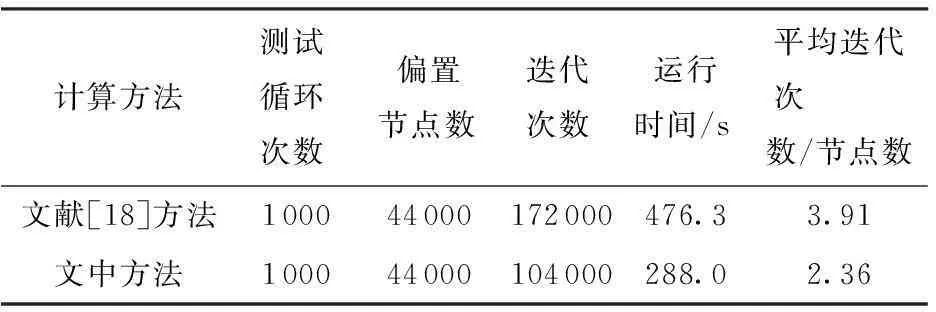
Table 1　Comparison of test results between two methods

为了将表面势近似解结果应用在器件的紧凑电流模型中,文中对式(21)关于栅压微分项的连续性进行验证,结果绘于图4.图4表明,该微分项在整个栅压范围内是连续的,同时满足先增大后逐步减小的规律,低栅压条件下,曲线的峰值处可近似作为器件由弱积累向强积累状态转变的开始.

图4　不同沟道电势下与Vg1-VFBf的关系Fig.4　Relationship between and Vg1-VFBf with diffe-rent channel potentials

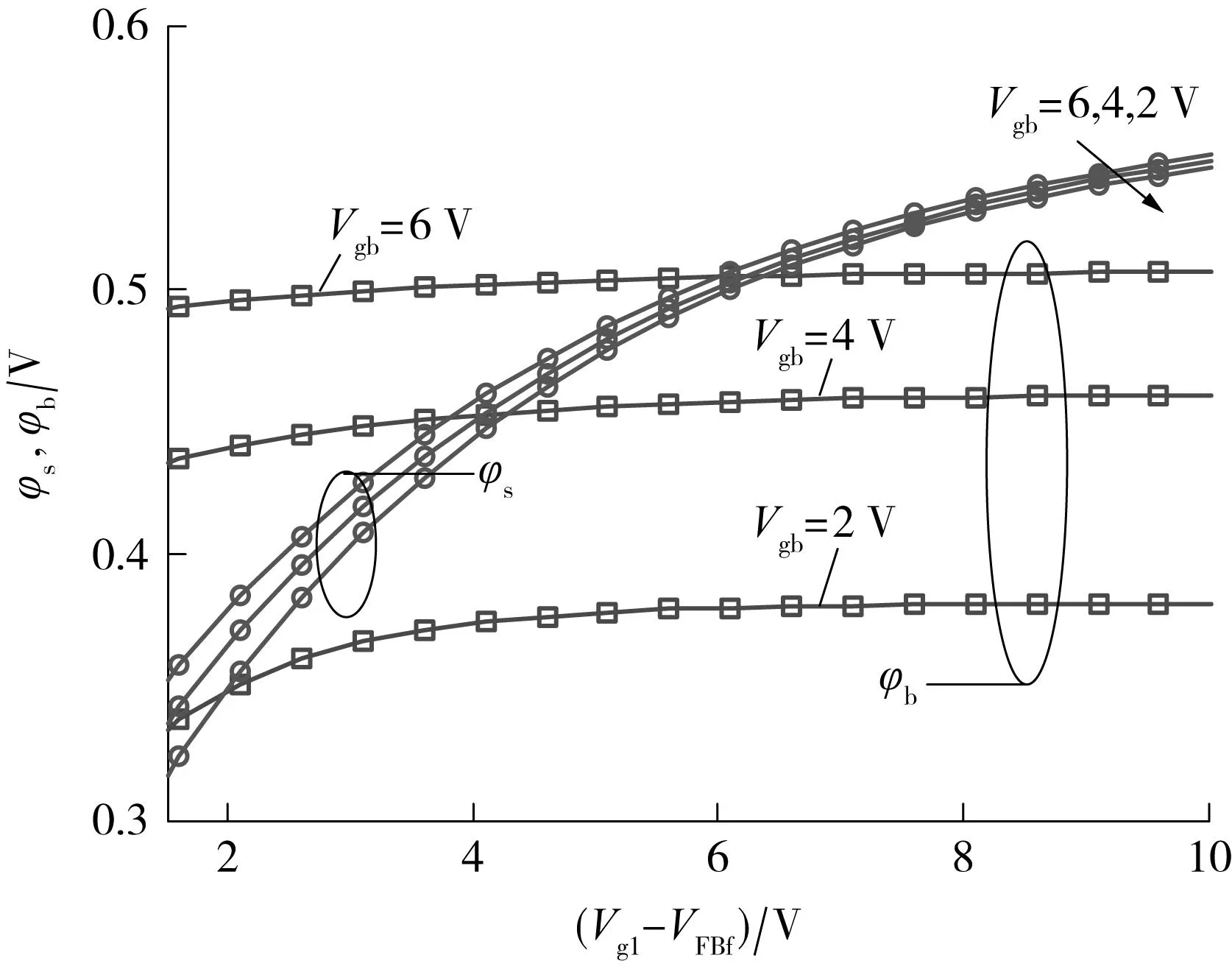
图5　不同背栅偏置条件下φs与φb随Vg1-VFBf的变化Fig.5　Changes of φs and φb with Vg1-VFBf under different back gate bias conditions

图5给出了不同背栅偏置下表面势及背电势随前栅压(Vg1-VFBf)的变化情况,其中toxf=250 nm,toxb=400 nm.图5表明,表面势随栅压的增大持续变大,在开启区域内依然呈现缓慢增长的趋势,而背电势随栅压的变化梯度在器件整个工作区域内远小于表面势,在开启区范围内基本上可认为被钉扎在一个固定的电势值上,该电势值由带尾态密度及有源层厚度共同决定,文献[5]给出了对称型双栅情况下该电势值的解析表达式.

图6给出了非对称条件下不同有源层厚度的表面势与背电势随前栅压的变化情况,其中toxf=toxb=200 mm,Vgb=0 V,有源层厚度与陷阱态参数与图3相同.图6表明,在相同界面陷阱态密度下,有源层越薄,电势在垂直于沟道方向上的变化梯度越陡.随着栅压的进一步增大,自由电子浓度在表面处随表面势呈指数形式快速增长,这种差异性逐渐缩小,这与器件的二维仿真结果相一致[11].

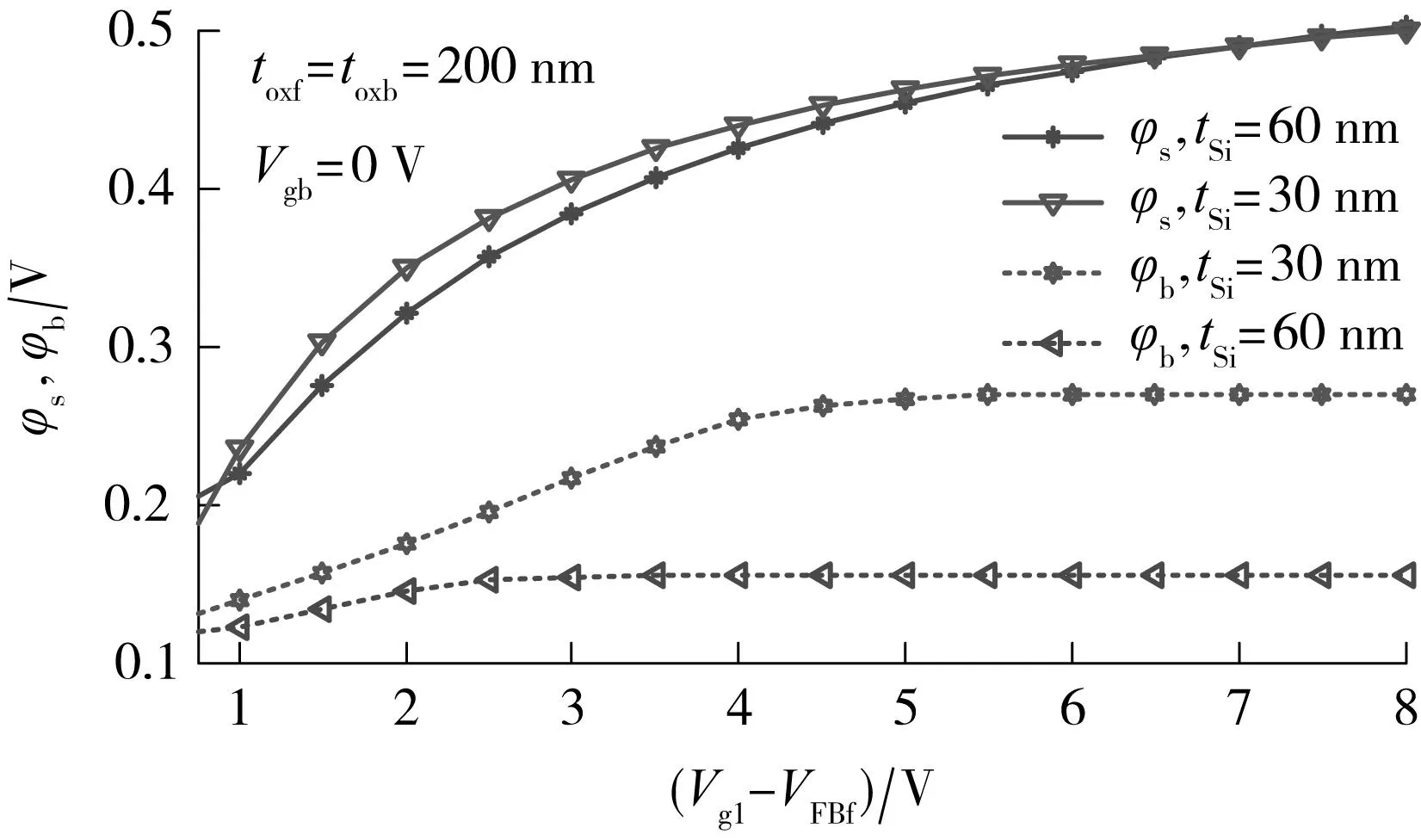
图6　非对称条件下φs与φb随Vg1-VFBf的变化Fig.6　Changes of φsand φbwith Vg1-VFBfunder asymmetrical condition

图7给出了不同有源层厚度下对称双栅器件表面势与中点电势随栅压的变化情况.图7表明,有源层越厚,体内钉扎的电势值越低.此外,亚阈环境下,表面势与中点电势的数值差随有源层厚度的减小显著增加,显示了自由电子在a-Si:H/Si:Nx界面处的快速积累.随着栅压的增大,界面处快速增长的自由电子对外电场形成屏蔽效应,有源层厚度对表面势的影响基本上可以忽略,与图6示出的结论相同.由于a-Si:H存在大量的陷阱态,在亚阈环境下表面势与有效偏压的比值远低于1,器件工作在弱积累状态,亚阈斜率由界面处深能陷阱态密度主导,并不存在体反型态,这一特性应与全耗尽DG MOSFETs有所区分[19].

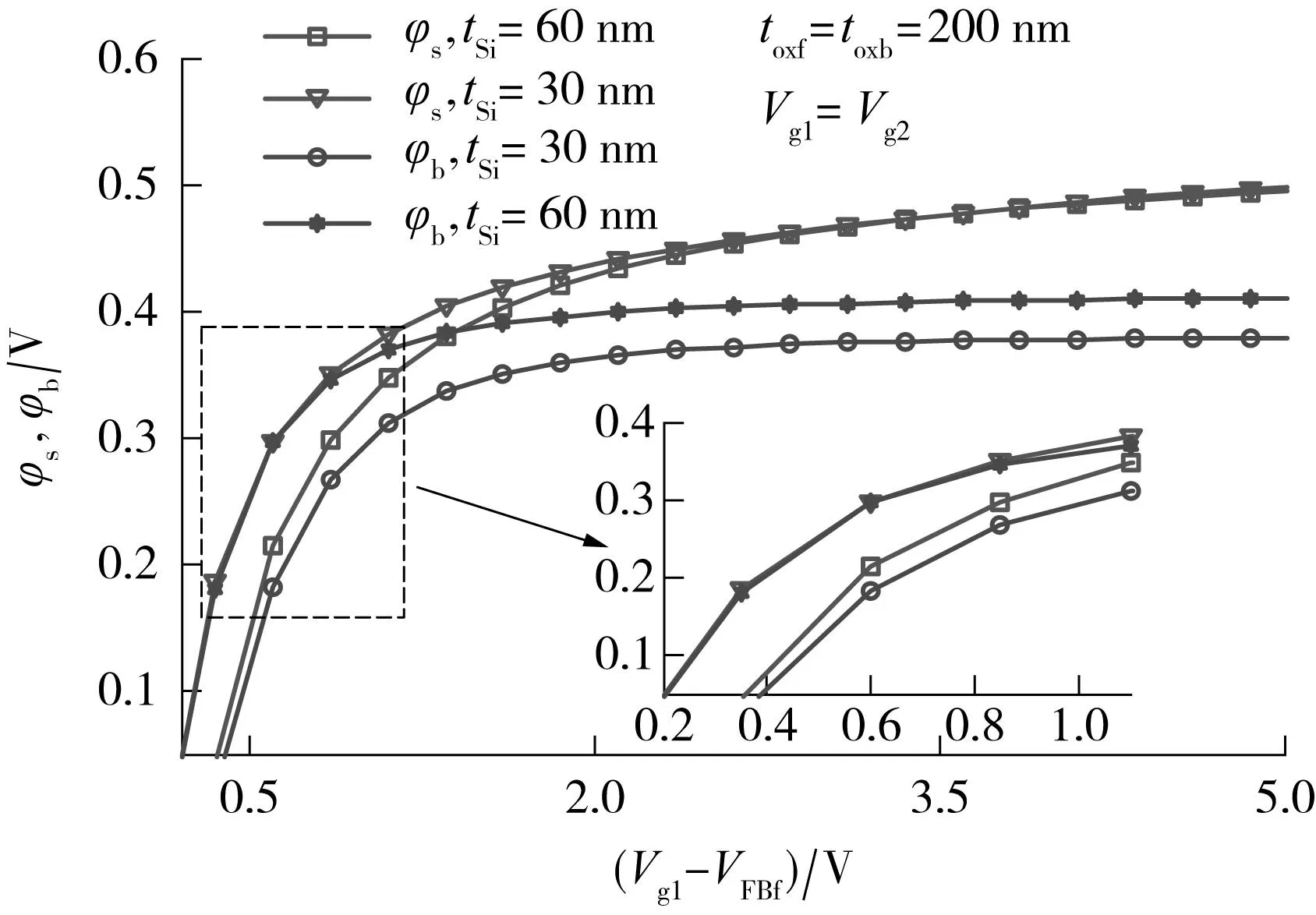
图7　对称条件下φs与φb随Vg1-VFBf的变化Fig.7　Changes of φsand φbwith Vg1-VFBf under symmetrical condition

3结论

应用等效特征温度近似方法,文中推导得到了独立偏置条件下aDG a-Si:H TFT统一的沟道电势模型,提出了沟道电势与栅压隐含关联方程的近似求解方法.数值模拟结果表明:表面势在垂直于沟道方向上的变化梯度远大于背电势,背电势在开启区被认为近似地钉扎在一个固定的数值上;前、后栅级对器件阈值电压的调制影响并不一致,平移阈值量取决于双栅绝缘层介电常数及相对厚度的比率、有源层厚度及界面陷阱态密度;文中模型所需拟合参数少,在特定条件下可简化为对称双栅的情形,文中给出的表面势近似解与数值模拟结果间的绝对误差随栅压增长快速收敛至10-5左右,可直接用于器件模拟软件的初值设定,有效提升模型自洽解的解算效率.下一步将利用此结果建立基于表面势的器件紧致漏电流模型.

参考文献:

[1]TAKECHI K,IWAMATSU S,YAHAGI T,et al.Characterization of top-gate effects in amorphous InGaZnO4thin-film transistors using a dual-gate structure [J].Japanese Journal of Applied Physics,2012,51(10):104201/1-7.

[2]LI Xiuling,GENG Di,MATIVENGA M,et al.High-speed dual-gate a-IGZO TFT-based circuits with top-gate offset structure [J].IEEE Electron Device Letters,2014,35(4):461- 463.

[3]BAUDRAND H,AHMED A.New model for submicron-scale dual-gate TFT [J].IEEE Electronics Letters,1984,20(1):33-35.

[4]YOUNG K K.Short-channel effect in fully depleted SOI MOSFETs [J].IEEE Transactions on Electron Devices,1989,36(2):399- 402.

[5]QIN Jian,YAO Ruo-he.A physics-based scheme for potentials of a-Si:H TFT with symmetric dual gate conside-ring deep Gaussian DOS distribution [J].Solid-State Electronics,2014,95(1):46-51.

[6]LIANG C Y,GAN F Y,YEH F S,el al.Letter:mechanisms for on/off currents in dual-gate a-Si:H thin-film transistors using indium-tin-oxide top-gate electrodes [J].Journal of the Society for Information Display,2007,15(1):975-977.

[7]SERVATI P,KARIM K S,NATHAN A.Static characteristics of a-Si:H dual-gate TFTs [J].IEEE Transactions on Electron Devices,2003,50(4):926-932.

[8]TAKECHI K,NAKATA M,AZUMA K,et al.Dual-gate characteristics of amorphous InGaZnO4thin-film transistors as compared to those of hydrogenated amorphous silicon thin-film transistors [J].IEEE Transactions on Electron Devices,2009,56(9):2027-2033.

[9]YANG C S,READ W W,ARTHUR C,et al.Self-aligned gate and source drain contacts in inverted-staggered a-Si:H thin-film transistors fabricated using selective area silicon PECVD [J].IEEE Electron Device Letters,1998,19(6):180-182.

[10]ORTIZ-CONDE A,GARCA SNCHEZ F J,MUCI J,et al.Rigorous analytic solution for the drain current of undoped symmetric dual-gate MOSFETs [J].Solid-State Ele-ctronics,2005,49(4):640- 647.

[11]MOON K H,CHO Y-S,CHOI H,et al.Characteristics of amorphous silicon dual-gate thin film transistor using back gate of pixel electrode for liquid crystal display driver [J].Japanese Journal of Applied Physics,2009,48(3):03B017/1- 4.

[12]LING W,FJELDLY T A,INIGUEZ B,et al.Self-heating and kink effects in a-Si:H thin film transistors [J].IEEE Transactions on Electron Devices,2000,47(2):387-397.

[13]Chen S S,Kuo J B.An analytical saturation region model for amorphous silicon thin film transistors using a quasi-two-dimensional and an effective temperature approach [J].Journal of Applied Physics,1994,75(12):7935-7941.

[14]LIU Yuan,YAO Ruo-he,LI Bin,et al.An analytical model based on surface potential for a-Si:H thin-film transistors [J].Journal of Display Techonology,2008,4(2):180-187.

[15]KANEKO Y,TSUTSUI K,TSUKADA T.Back-bias effect on the current-voltage characteristics of amorphous silicon thin-film transistors [J].Journal of Non-Crystalline Solids,1992,149(3):264-268.

[16]刘远,姚若河.非晶硅薄膜晶体管中不饱和输出电流的数值仿真 [J].华南理工大学学报(自然科学版),2009,37(1):15-18.

LIU Yuan,YAO Ruo-he.Numerical simulation of unsa-turated output current of amorphous silicon thin film transistors [J].Journal of South China University of Technology(Natural Science Edition),2009,37(1):15-18.

[17]CERDEIRA A,ESTRADA M,GARCIA R,et al.New procedure for the extraction of basic a-Si:H TFT model parameters in the linear and saturation regions [J].So-lid-State Electronics,2001,45(7):1077-1080.

[18]ZHU Zhengyong,PENG He,CHENG Chung-Kuan,et al.Two-stage Newton-Raphson method for transistor-levelsimulation[J].IEEETransactionsonComputer-AidedDesignofIntegratedCircuitsandSystems,2007,26(5):881-895.

[19]LIU F,HE J,ZHANG J,et al.A non-charge-sheet analytic model for symmetric double-gate MOSFETs with smooth transition between partially and fully depleted operation modes [J].IEEE Transactions on Electron Devices,2008,55(12):3494-3502.

A Unified Channel Potential Model for Asymetrical Dual

Gate a-Si:H Thin Film Transistors

QINJianYAORuo-he

(School of Electronic and Information Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China)

Abstract:On the basis of the Gauss’s law, two sets of implicit potential equations describing the changes of surface potential and back one with gate voltage are established for asymmetrical dual gate a-Si: TFT thin film transistors. Then, a unified channel potential model with two independent gates is constructed by solving 1-D Poisson equations. This model can be simplified to a symmetric dual gate model under given conditions. In addition, most of relevant parameters can be physically extracted from real experimental data and only few fitting parameters are involved. On this basis, a novel scheme for the approximation of surface potentials is proposed by means of mathematical transformation and by using the Lambert W function. Numerical results show that the proposed scheme is of better convergence and the approximation of those potentials can be directly used to set the initial values of simulation tools, which effectively improves the computation efficiency of self-consistent solutions to the constructed model.

Key words:asymetrical dual gate thin film transistor; surface potential; a-Si:H; density of states; approximate solution

doi：10.3969/j.issn.1000-565X.2016.01.005

中图分类号：TN321

作者简介：秦剑(1981-)，男,博士生,讲师,主要从事薄膜晶体管TFT的制备与建模研究.E-mail:gzu_jyuan@163.com†通信作者： 姚若河(1961-),男,教授,博士生导师,主要从事集成电路系统设计、半导体物理及器件研究.E-mail:phrhyao@scut.edu.cn

*基金项目：国家自然科学基金资助项目(61274085)

收稿日期：2015-05-11

文章编号：1000-565X(2016)01- 0030- 07

Foundation item： Supported by the National Natural Science Foundation of China(61274085)