锥度球头立铣刀磨削加工数学模型研究*

夏文胜，赵先锋，高　飞，周兆锋

(1.盐城工学院 机械工程学院，江苏 盐城　224051；2.贵州大学 机械工程学院，贵阳　550025)



锥度球头立铣刀磨削加工数学模型研究*

夏文胜1，赵先锋2，高飞1，周兆锋1

(1.盐城工学院 机械工程学院，江苏 盐城224051；2.贵州大学 机械工程学院，贵阳550025)

摘要：针对锥度球头立铣刀的几何特征，根据锥度球头立铣刀的成型原理，利用微分几何的基本原理，研究了锥度球头立铣刀前后刀面的刀刃曲线建模方法，设计了一种新的锥度球头立铣刀刀刃曲线，并借助Visual Basic语言，利用SolidWorks软件对所设计的刀刃曲线进行了建模和验证。为锥度球头类刀具的进一步设计提供了理论方法和依据。

关键词：锥度球头立铣刀；磨削加工；前后刀面；数学模型

0引言

合理的刀具数学模型是加工制造刀具研究的基础。锥度球头立铣刀制造的关键技术在于球头部分的加工。锥度球头立铣刀的切削性能与球刃的S形密切相关，较好的S形刃和合理的几何参数分布是锥度球头立铣刀切削性能的保证，如何获得较好的S形刃和合理的几何参数分布是锥度球头立铣刀制造的关键。在现有的研究中，锥度球头立铣刀球刃模型大多采用的球刃曲线是正交螺旋面和球面的交线[1-2]。我们在研究圆柱球头立铣刀的制造过程中提出了新的前刀面数学模型[3]，并将其拓展为锥度球头立铣刀的数学模型，利用这种建模方法加工出来的锥度球头立铣刀，球头与锥刃的螺旋槽槽底刀刃曲线能够实现光滑连接。

1锥铣刀前刀面数学模型

1.1球刃前刀面数学模型

1.1.1球刃前刀面成形原理

我们提出了新的前刀面数学模型，其磨削运动关系由沿X、Y、Z三个方向的平移运动和绕铣刀轴线的旋转运动构成。锥度球头立铣刀前刀面磨削加工过程中砂轮与铣刀的位置关系如图1所示。

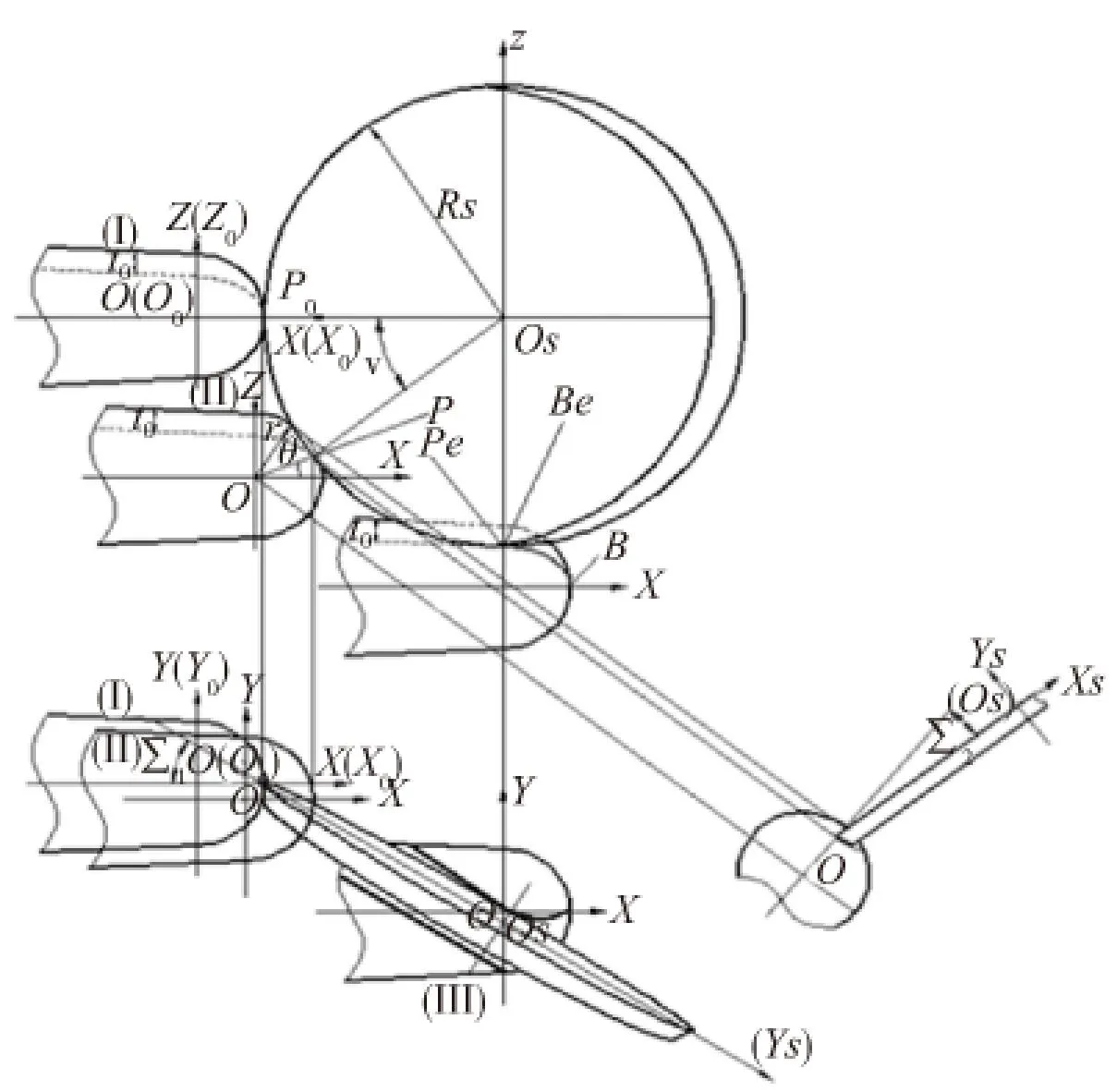
图1　锥铣刀前刀面磨削运动关系图

BBe为锥度球头立铣刀前刀面的槽底曲线，砂轮与工件发生相对运动时砂轮大圆圆周p0ppe始终与槽底曲线BBe相切，在工件上形成螺旋槽前刀面。在前刀面磨削加工过程中，从砂轮较大圆的端面圆周开始与槽底曲线的起点B相切开始，直至砂轮较大圆的端面最低点pe与槽底曲线的终点Be相切结束。由于螺旋槽的侧面点的螺旋升角各不相同，螺旋槽侧表面是扭曲的。为了避免砂轮与工件螺旋槽发生干涉甚至产生过切，安装角∑1应比螺旋角β大1°～3°，则：∑1=β+(1°~3°)。为了使本磨削加工方法更具有通用性，将砂轮圆周端面绕砂轮大圆面上水平轴转动∑2角度。为此建立以下三个坐标系(见图1)：

工件坐标系σ=[O;X,Y,Z]：以锥度球头立铣刀球头的球心为坐标原点O；

砂轮坐标系σS=[OS;XS,YS,ZS]：OS在砂轮大圆的圆心，OSXSZS在砂轮大圆面内，YS垂直OSXSZS。

机床坐标系σ0=[O0;X0,Y0,Z0]：为了计算方便，假设机床坐标系σ0与工件坐标系σ的初始位置重合，坐标原点在锥度球头立铣刀的球心O位置。

1.1.2球刃前刀面数学模型

锥度球头立铣刀的槽底曲线在XZ平面上为椭圆线：[srcosθ,0,sr(1-c)sinθ]，在空间为椭球体螺旋线：[srcosθ,sr(1-c)sinθsinω,sr(1-c)sinθcosω]。

其中：c—槽深系数

sr—球头半径

ω—锥铣刀绕X轴转动角度，且0°≤ω≤90°

θ—与X轴夹角0°≤θ≤90°θ=θ0t(θ0为转动的角速度)

即在坐标系内，球头部分的槽底曲线为：

(1)

又空间曲线为等螺旋角[3]：

(2)

其中：β—螺旋线的螺旋升角

p—为导程

可得

p=2πsr(1-c)tanβ

(3)

在砂轮坐标系下，砂轮的平面(大圆面)方程：

(4)

砂轮的平面法线方程为：

(5)

砂轮在固定坐标系下起始位置：

砂轮要绕X轴旋转∑2，绕Z轴旋转∑1，然后在Y方向平移距离为rsin∑1，在X方向平移距离为(sr+r)坐标变换过程为：

①绕X轴旋转∑2

②绕Z轴旋转∑1

③Y方向平移距离为rsin∑1

④X方向平移距离为(sr+rcos∑1)

变换矩阵分别为：

绕X轴旋转∑2

(6)

绕Z轴旋转∑1

(7)

Y方向平移矩阵(Y负方向)

(8)

X方向平移矩阵

(9)

可得变换矩阵为：

T=TrxTrzTtyTtx

(10)

即：

(11)

砂轮的平面方程在固定坐标系下起始位置为：

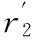
rcosηsin∑1-rsinηsin∑2cos∑1-rsin∑1

rsinηcos∑21]

(12)

即：

(13)

法线方程在固定坐标系下起始位置为：

(14)

-rcos∑2cos∑1+rsin∑-rsin∑21|

(15)

即：

(16)

下面求θ与η的关系：

槽底曲线旋转到XOZ平面，可得：

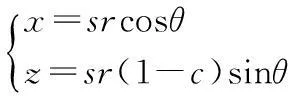
(17)

砂轮轮廓曲线投影到XOZ平面：

(18)

槽底曲线的切率：

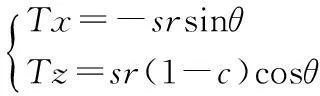
(19)

砂轮轮廓曲线切率：

(20)

两者相切：

(21)

推导出θ与η的关系：

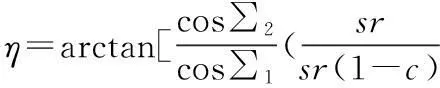
(22)

而θ与ω的关系：

(23)

砂轮大圆面方程：

(24)

砂轮绕X轴旋转ω，其包络面为：

(25)

(26)

整理得前刀面的方程：

(27)

即

(28)

1.2周刃前刀面数学模型

1.2.1周刃前刀面成形原理

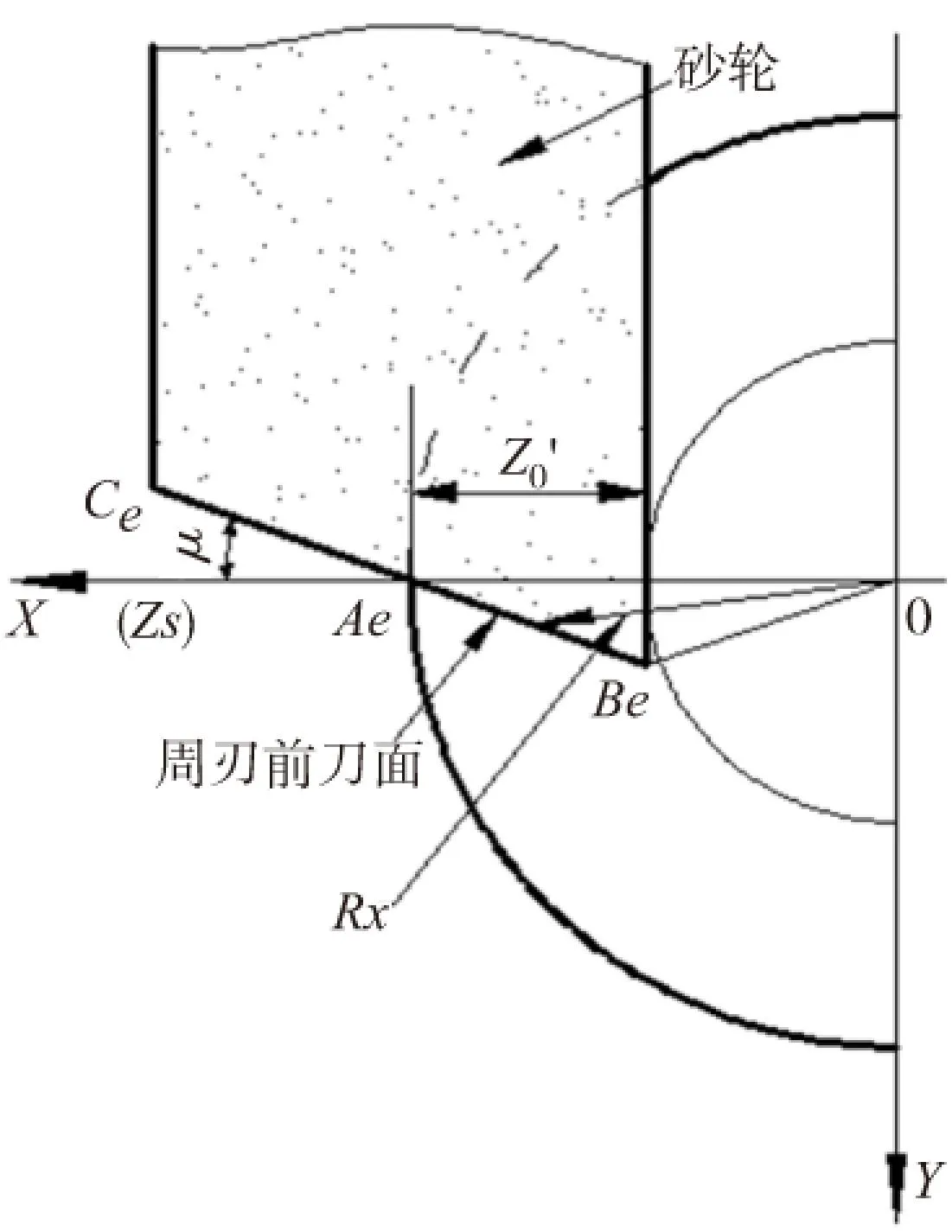
图2　周刃前刀面的数学模型

球刃前刀面按上述方法形成后，B点到达Be点，即形成母线BC到达图2所示位置。砂轮相对于铣刀作螺旋运动和轴向移动同时，砂轮还有一个远离刀具轴线的运动，这样，在工件上形成的螺旋槽，就由砂轮与工件接触弧长的那一部分圆周产生[3-4]。在锥度球头立铣刀制造过程中一次性依次完成球刃和周刃的加工，因此在磨削加工完球刃后，砂轮相对于工件作螺旋运动，周刃前刀面就是砂轮母线运动的包络面。

1.2.2周刃前刀面数学模型

圆锥螺旋部分的槽底曲线，根据《数学在刀具设计中的应用》[5]，实际是圆锥螺旋线，为：

(29)

其中：β为螺旋线的螺旋升角

根据成形原理，可以推导出周刃前刀面的数学表达式。推导过程与球刃前刀面的推导过程相似，这里不再重复叙述。只给出推导结果，即周刃前刀面的数学表达式为：

(30)

式中m0—被加工螺旋槽部分的角度;

Rz—周刃前刀面上任一点的半径，其计算公式为：

(31)

其中μ为砂轮母线与砂轮轴线的夹角，即圆锥砂轮的半锥度。

2锥铣刀后刀面的数学模型

2.1后刀面磨削加工满足的条件

锥度球头立铣刀后刀面与直柄球头立铣刀相比，同样包括球刃后刀面和周刃后刀面，球头刀刃的形成是由球刃后刀面决定的。因此，加工球刃后刀面时，有两个需要注意的地方。

(1)必须确保刀具的切削刃不能遭到任何破坏。在磨削加工锥铣刀后刀面的过程中，要尽量避免砂轮与球刃间的干涉，不偏离也不能过切。因此在磨削加工过程中，为了保证切削刃没有遭到破坏，砂轮母线上始终要有一点与球刃相切触。

(2)要求按等主后角来磨削加工。锥度球头立铣刀刀齿的使用寿命，也就是锥铣刀刀赤的切削性能和磨损程度，是由球刃主后角来决定的。同时，从加工的角度来说，为了在加工过程中减小铣刀的振动，后刀面的加工要求按等后角来磨削。但是，由于锥铣刀球刃上各点的刃倾角各不相同，而且大多数情况下，按等法向后角来调整砂轮的位置，因此在球刃后刀面的磨削加工过程中会导致球刃各点的主后角不同[6]。

2.2球刃后刀面的磨削加工方法与数学模型

2.2.1后刀面的磨削加工方法

图3　后刀面的成形运动

根据前刀面的成形原理，铣刀以角速度ω1绕回转中心公转，同时以K1ω1自转。为了满足后角的要求，砂轮轴线与铣刀轴线之间存在一个高度差h。在磨削加工过程中，铣刀绕球头球心O以角速度ω2公转，同时绕自身轴线以K2ω2转动，如图3所示。为了保证已经形成的刃口不被破坏，ω1与ω2，K1ω1与应满足ω2=f1(ω1)，K2=f2(K1)。根据上述成型原理，建立铣刀后刀面数学模型。

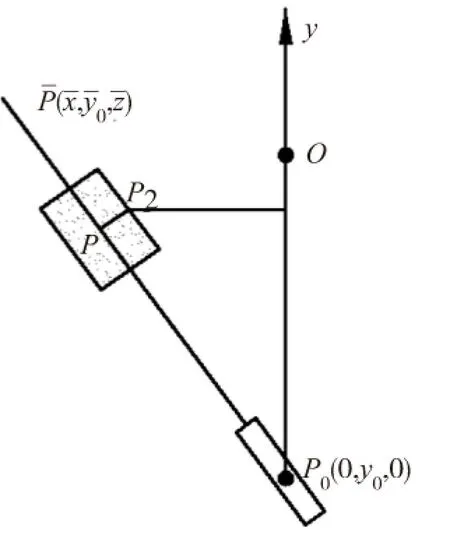
图4　后刀面的加工原理

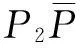
2.2.2后刀面数学模型—等主后角磨削加工

(1)重要曲线——曲线的法向等距线

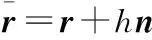
(32)

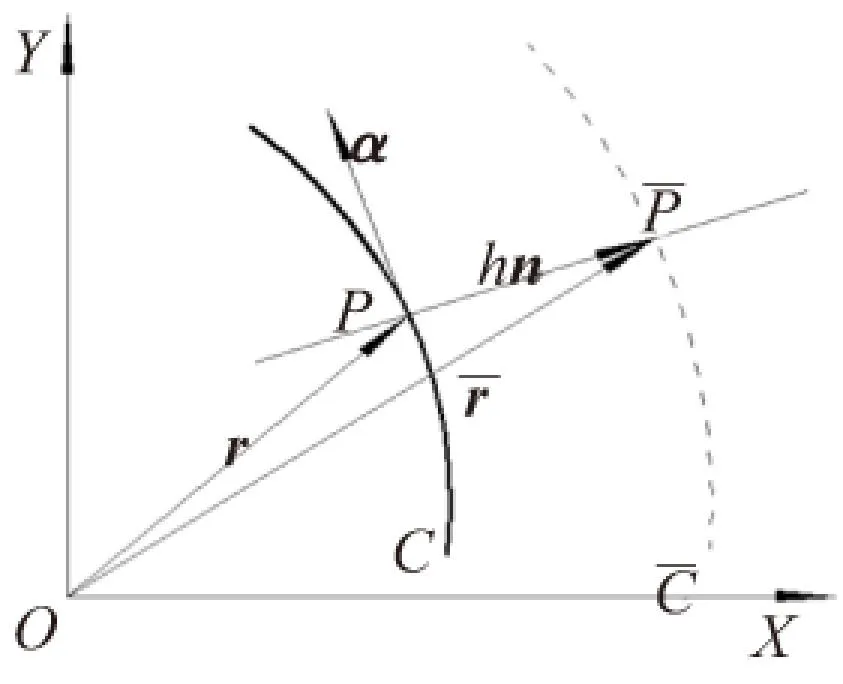
图5　曲线的法向等距线

对于空间曲线上任意一点的法向矢量不是唯一的，因此其法向等距线也不唯一，但是我们知道空间曲线上任意一点法向矢量n可以根据该点的唯一幺切矢α0和主幺法矢n0获得，为此引入如下定理：

(2)一个重要定理

矢量旋转定理[9]：空间坐标系中，一个矢量n0绕另一矢量α0旋转αn角后，所得到的新矢量n可以表示为：

n=n0cosαn-(α×n0)sinαn

(33)

下面结合后刀面的磨削条件，赋予上述定义及定理的物理意义。

(3)后刀面的数学模型

后刀面磨削加工的数学模型，如图6所示，设砂轮母线上一点要与S形刃相切并且相接触，并且保持砂轮轴线和切点处的切线矢量平行，切点处铣刀应具有已知的法向后角αn,，满足这些条件的砂轮中心轨迹必为S形刃的一条法向等距线。如图7所示，设坐标系为加工前刀面坐标系σ=[O;X,Y,Z]，在S刃上取任意点p，设砂轮的半径为R1，在p点相切，则p点S刃的法向等距线方程为：

r1=r+R1r0

(34)

图6　后刀面的数学模型

图7　S刃的法向等距线

幺法矢r0可由切点p处球面主幺法矢N1绕该点处端刃切幺矢T0旋转αn求得：

r0=N1cosαn-(T0×N1)sinαn

(35)

下面求p点端刃切幺矢T0：

如图8所示，设p(X,Y,Z)为锥度球头立铣刀球刃主切削刃所求点的坐标，则球面上该点处的单位法矢N1为：

(36)

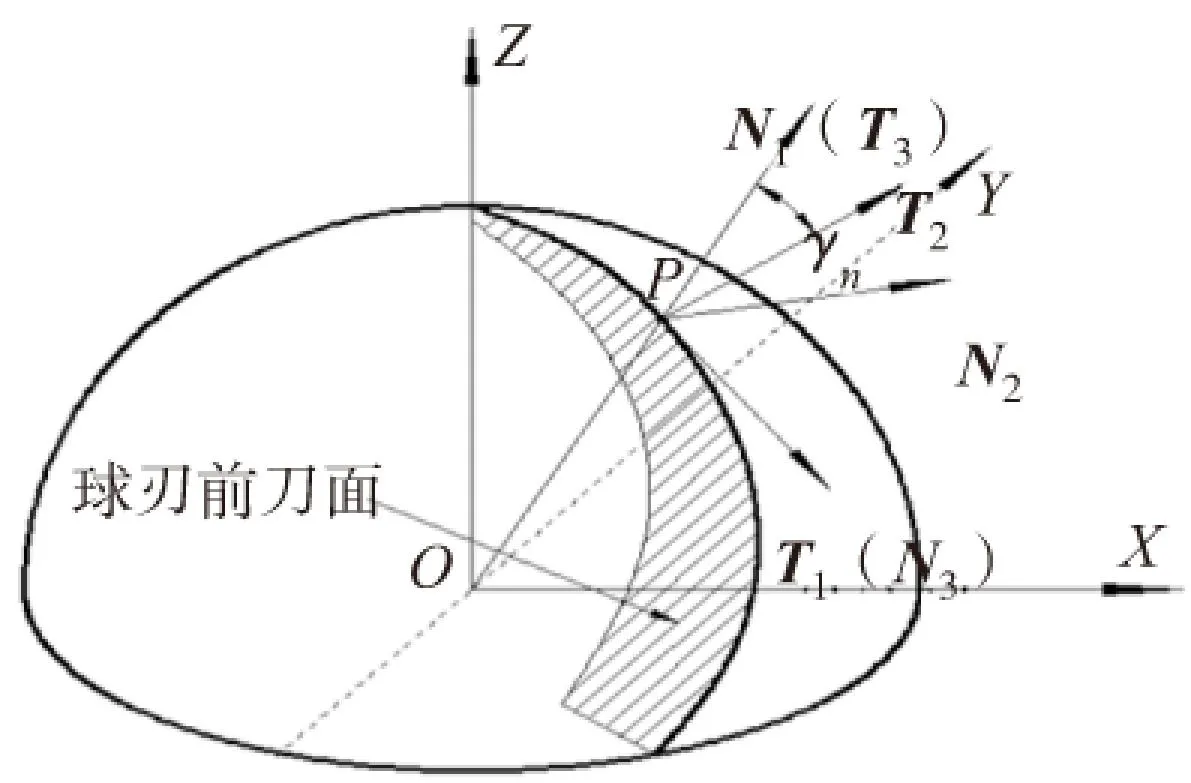
图8　法前角示意图

球头前刀面在该点的法矢N2为：

(37)

球刃主切削刃上在该点(X,Y,Z)的切矢T1=N1×N2，即：

T1=(N1YN2Z-N2YN1Z)i+(N1ZN2X-N2ZN1X)j+

(N1XN2Y-N2XN1Y)k

(38)

而

(39)

由于是等主后角磨削加工，给定的是主后角α0，根据《金属切削原理》[10]求出法向后角αn。

ctgαn=ctgα0×cosλs

(40)

联系式(34)、(35)、(39)、(40)可得到S形球刃的法向等距线方程，由于以上求导过程和矢量运算比较复杂，本文只给出其表达式。

r1=

(41)

3磨削仿真加工实例

3.1前刀面的磨削仿真加工

依据实际加工过程，以SolidWorks为操作平台，VB为开发工具，建立锥度球头立铣刀磨削仿真加工系统。此虚拟加工系统充分利用SolidWorksApI的方法与属性，选用直接实体造型法来实现复杂曲面仿真加工。

按照锥度球头立铣刀前刀面形成的位置关系编制合理的运动程序，用程序控制砂轮的各种运动，通过实体间的布尔差运算来实现砂轮实体对铣刀毛坯实体的切除加工，从而形成球刃与周刃前刀面，前刀面的仿真结果如图9所示。可以看出：锥度球头立铣刀的球刃为S形弧形刃，刃形曲线较为理想；球刃前刀面与周刃前刀面能实现光滑连接。

(a)S形刃　　　　　(b)S形刃在球头和圆锥结合处

3.2后刀面的磨削仿真加工

利用前刀面磨削仿真加工的结果来实现后刀面的磨削仿真加工。按照磨削锥度球头立铣刀前刀面形成的位置关系，通过程序选出所有主切削上的点，根据这些被选中的点，编制合理的运动程序，同样利用程序控制砂轮的移动和偏转，通过实体间的布尔差运算，实现砂轮实体对铣刀毛坯实体的切除加工，从而形成球刃后刀面和周刃后刀面，如图10所示。

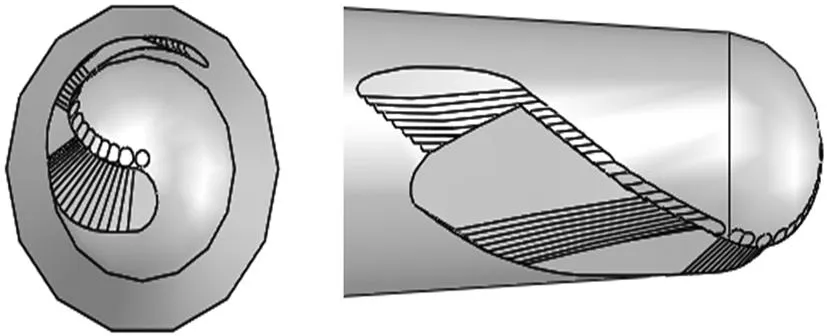
(a)球刃后刀面　　　　　(b)周刃后刀面

4结束语

本文以锥度球头立铣刀的正交螺旋形的刀刃曲线为基础，根据锥度球头立铣刀前后刀面的成形原理，分别建立了锥度球头立铣刀数学模型，他们具有等法向前角的前刀面、等主后角的后刀面。最后利用该模型建立了锥度球头立铣刀磨削加工仿真与分析系统，以检验模型的正确性。该模型及其仿真设计软件为锥度球头立铣刀的设计、制造与进一步开发提供了理论方法与基础。

[参考文献]

[1] 盛尚雄,吴卓,马世辉. S 形刃球头立铣刀的数学模型[J]. 甘肃科学学报, 2009,21(4): 104-108.

[2] 李清,王太勇,吉洪武. 基于物理仿真模型的螺旋立铣刀建模[J]. 组合机床与自动化加工技术,2005(8):19-22.

[3] 李帅. 新型球头立铣刀前刀面刃磨仿真研究[D]. 贵州:贵州大学,2008.

[4] 康长玉,朱斌,雷君相. 利用数控改造加工等螺旋角等前角锥球头立铣刀[J]. 制造技术与机床, 2010(6): 129-131.

[5] 姚南珣. 数学在刀具设计中的应用[M]. 北京:机械工业出版社,1986.

[6] 韩政峰. 基于四轴磨削加工的球头立铣刀数学模型研究[D]. 贵州:贵州大学, 2008.

[7] 唐余勇，汪兴涛，鲍青山. 非数控加工球头铣刀的主干数学模型[J]. 工具技术,2002,36 (3):19-21.

[8] 黄宣国. 空间解析几何与微分几何[M]. 上海:复旦大学出版社,2003.

[9] 吴丛炘,唐余勇. 微分几何讲义[M].北京:高等教育出版社,1985.

[10] 陆剑中，孙家宁.金属切削原理与刀具[M]. 5版.北京:机械工业出版社,2011.

(编辑李秀敏)

Research on Grinding Mathematical Models of the Taper Ball-nose End Milling Cutter

XIA Wen-sheng1, ZHAO Xian-feng2, GAO Fei1, ZHOU Zhao-feng1

(1.School of Mechanical Engineering, Yancheng Institute of Technology, Yancheng Jiangsu 224051,China; 2. School of Mechanical Engineering, Guizhou University, Guiyang 550025, China)

Abstract：For geometrical features of taper ball-nose end milling cutter, according to the forming principle of taper ball-nose end milling cutter, with the basic principles of differential geometry, the modeling method for edge curves of taper ball-nose end milling cutter was studied and a novel edge curve of taper ball-nose end milling cutter was designed. Beside，with the Visual Basic language, the edge curve which designed was modeled and verified by using SolidWorks. As a result, a theoretical method and basis for the further design of taper ball-nose end milling cutter was provided.

Key words：taper ball-nose end milling cutter; grinding ; rake and flank; mathematical model

中图分类号：TH162;TG506

文献标识码：A

作者简介：夏文胜(1984—)，男，江苏阜宁人，盐城工学院讲师，工学硕士，从事机床、刀具与模具方面的教学科研工作，( E-mail)xws2222@126.com。

*基金项目：贵州省科技厅重点科技项目：高性能球头立铣刀工具磨的研制[黔科合GZ字(2007)3008]

收稿日期：2014-10-24；修回日期：2014-11-27

文章编号：1001-2265(2016)01-0122-05

DOI:10.13462/j.cnki.mmtamt.2016.01.034