基于THDMOpSO绿色减速器模块划分不确定优化*
2016-02-24刘电霆张全永
刘电霆,张全永
(桂林理工大学 a.机械与控制工程学院;b.信息科学与工程学院,广西 桂林 541004)
基于THDMOpSO绿色减速器模块划分不确定优化*
刘电霆a,张全永b
(桂林理工大学 a.机械与控制工程学院;b.信息科学与工程学院,广西 桂林541004)
摘要:针对含不确定的变量或参数的多目标问题,以减速器的模块化绿色配置设计为例,引入区间数和模糊数作为变量,研究了绿色设计中包含不确定因素的产品模块划分问题,给出了模块划分的原则和主要步骤,以模块内部聚合度最大、模块之间耦合度最小和模块划分所得绿色度最高为多目标函数,建立了产品绿色模块划分的不确定优化模型,对其中区间数和三角模糊数确定化后,提出THDMOpSO方法进行求解,通过减速器结构模块构造进行验证,表明此方法具有可行性和生产实用价值。
关键词:不确定优化;绿色设计;模块化设计;十进制离散多目标粒子群算法
0引言
在绿色设计[1-3]成为企业产品设计标配的时代,绿色产品的模块化设计迎合了现代化设计的理念,已经开始从大批量生产向大规模定制转变,各种绿色配置设计和组合设计正浮出水面。近年来,针对绿色模块化设计问题的研究成为热点,但在已有研究中很少有人考虑设计过程中的不确定性因素以及离散多进制多目标粒子群算法求解[4-11]。
本文基于现有减速器的绿色模块划分方法,并考虑其中存在的不确定因素和绿色设计等目标,从建立不确定模型入手,引入pareto 集理念,提出一种十进制多目标离散粒子群方法,求解并验证所提出的方法的有效正确性,具有生产实用性。
1案例分析及建模
1.1问题的描述
在绿色设计中产品族模块划分的原则可简记为:高内聚低耦合。高内聚指模块内部的聚合度尽量大即模块内部之间的关联应该尽量大;低耦合指模块之间的耦合度尽量小即模块之间的交互应该尽量少;同时还应该考虑其绿色性尽量达到最优。以一个减速器为例,实际生产中减速器结构分为五大模块,共十个基本单元,通过功能相关性分析,把同一功能的基本单元尽量聚合成一个模块,以提高模块的功能独立性。通过结构相关性分析,尽量使结构相关的划在一个模块以保证结构的完整性。它们的相关性大小是一种定性问题,可用三角模糊数来描述。比如功能相关性从弱到强有属性“无”,“一般”,“较强”,“强”,“极强”等特性,可用三角模糊数[0.0,0.0,0.0],[0.0,0.2,0.4], [0.2,0.4,0.6], [0.4,0.6,0.8], [0.6,0.8,1]表示,同理可以进行结构相关性的表示,考虑到篇幅限制,这里不再累述。
在确定了功能和结构的度量后,绿色设计中产品族模块划分时必然要有一些绿色准则,本文设有回收性、维护性、升级性、重用性、处理性等5个准则,对每个绿色准则的度量可采用区间数值表示,如表3所示。
1.2相关数据建立
减速器结构由联轴器、润滑、齿轮、轴、箱体、轴承、端盖、密封、螺钉、键等10个基本单元组成。本文分别用T1、T2、T3、T4、T5、T6、T7、T8、T9、T10表示。其功能关联矩阵和结构关联矩阵数值如表1和表2所示[12]。

表1 减速器功能关联表

表2 减速器结构关联表
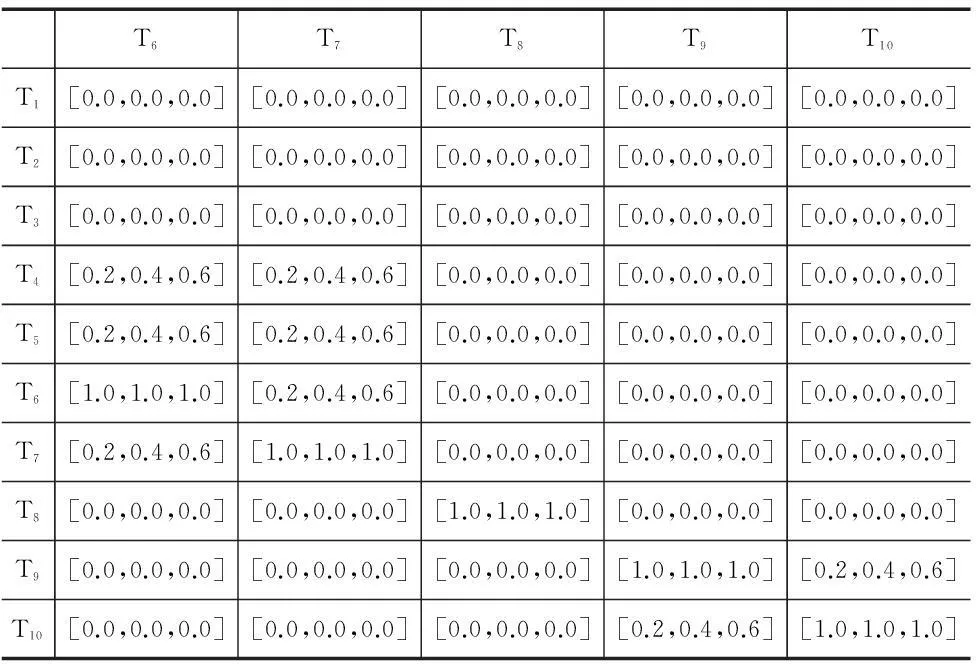
续表
考虑无量纲化后T1、T2、T3、T4、T5、T6、T7、T8、T9、T10的绿色属性区间值见表3所示。
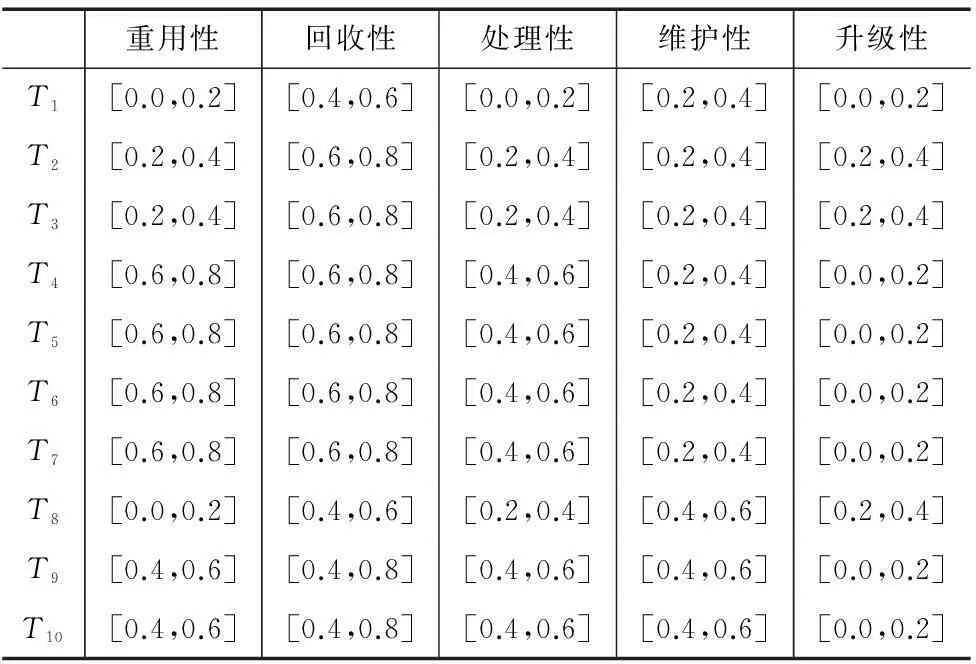
表3 绿色属性区间值
2模块划分不确定模型
2.1耦合度和内聚度以及绿色度模型
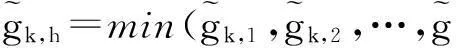
(1)
(2)
(3)
2.2三角模糊数的运算法则

本文采用加权重心法对三角模糊数进行确定化,即利用式(4)求得确定化数a:
(4)
2.3区间数的运算法则:
区间数有其自身的二元运算法则,同实数的二元运算法则类似,设两个区间数A=[aL,aR]和B=[bL,bR],令λ∈R,,则其对应的二元运算法则[15]如下。
(1)A-B=[aL-bL,aR-bR]
(2)λA=λ[aL,aR,]
(3)A+B=[aL+bL,aR+bR]
设带区间数的目标函数表示为Minf(X,U),则确定化转化方法如式(5):
f(X,U)=
[fL,(X)],fR(X)=
(5)
其中,
(6)
(7)
引入变量β作为权系数,且β∈[0,1], 可把目标函数Minf(X,U)转化为如下单目标形式,如式(8)所示:
min(βm(f(X,U))+(1-β)w(f(X,U)))
(8)
3十进制离散多目标粒子群算法的求解
3.1二进制离散粒子群算法
针对实际工程中存在的组合优化问题,Kennedy和 Eberhart[16]结合二进制和粒子群算法提出了离散版二进制粒子群算法即BpSO(Binary particle Swarm Optimization),很好的解决了该问题。在BpSO中对粒子的速度和位置公式进行了改进,用公式(9)、(10)取代。
v[i][j]=w*v[i][j]+c1*rand()*(l[i][j]-
p[i][j])+c2*rand()*(g-p[i][j]);
(9)
其中,若rand()<1/(1+e-v[i][j]),则p[i][j]=1;否则,p[i][j]=0;
(10)
3.2多目标问题模型
多目标问题的数学形式可以表示为如下模型:
Min y= f(x)=[f1(x),f2(x),…fn(x)]
n=1,2,…,N
s.tgi(x)0i=1,2,…m
hj(x)=0j=1,2,…k
X=[x1,x2,…,xD]
针对多个目标在大多数情况下不能同时达到最优的问题,通过不断协调各目标函数之间的关系,直到找出使各目标函数都能尽量达到最优的最优解集,通常称这种解为非支配解或 pareto 最优解[17]。
3.3pareto支配
定义1:支配关系[17-18]:对于∀a,b∈Z;若fn(a)≤fn(b),(n=1,2,…r);且y∈{1,2,…r},同时,有fy(a)< fy(b),则称a支配b,表示为 b。其中a>b,称a是非支配的,b是被支配的,“>”表示支配关系。
定义2:不相关关系:对于∀a,b∈Z;若a不支配b且b不支配a,则称a和b不相关或者互不支配。
3.4十进制离散多目标粒子群算法求解过程
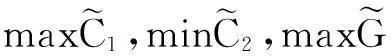
设功能关联的权重系数和结构关联的权重系数都为0.5,并设5个绿色准则的权重系数分别为:0.3564、0.2296、0.2296、0.0922和0.0922[19],β=0.8,定义n个精英解,n可根据实际情况变化。
十进制离散多目标粒子群优化(THDMOpSO)求解步骤如下:
(1)初始化粒子:设置相关的参数、局部最优集、定义n个精英集;将问题的解用十个随机的十进制数表示,产生相应粒子群,比如:0,0,1,8,9,5,5,9,9,0;2,2,3,6,6,6,2,5,7,7。数值相同就表示是同一个模块,有多少个不同的数值就有多少个不同的模块。
(2)更新位置值:在离散二进制基础上改进得到离散十进制,利用SIGMOID函数,在每位上按式(11)产生随机的离散十进制整数。
particle[i][j]=((int)((1/(1+exp(-v[i][j])))*
RAND_MAX))%10
(11)
(3)更新速度:局部最优解依旧选粒子本身的,全局最优值由n个精英解中随机产生一个作为全局最优解;按式(12)更新速度。
v[i][j]=w*v[i][j]+c1*1.0*rand()/RAND_MAX*
(loc_best[i][j]-particle[i][j])+c2*1.0*rand()/
RAND_MAX*(glo_best[随机][j]-particle[i][j])
;(12)
(4)更新局部最优解:计算多目标模型式(1)、(2)、(3),当前解与局部最优比较,如果非支配就更新,如果是互不支配就按式(13)进行均值比较,均值小的保留,fi代表目标函数。
(13)
(5)更新精英解:采用庄家法则,当前解分别与精英解集比较,删除精英解中被支配的解,同时让非支配解进入精英解集,如果是互不支配的解依据均值式(13)比较,让均值大的删除,腾出空间让均值小的进入精英解集。
(6)按式(13)依靠均值排序输出均值最小的最优解和n个精英解。
(7)如果达到迭代次数或理想结果就结束,否则转2步。
3.2实验数据
实验环境及参数设置:运行环境为C_FREE5.0,编写程序语言为C语言,粒子数目100个,学习因子C1=2,学习因子C2=3.5,惯性权重0.5,最大迭代次数为1000次,目标函数3个,精英解分别取为n=1,2,3个来做实验;获得的测试数据如表4。
表4实验数据

3.3实验分析
分析实验数据可知,收敛速度非常快,随着迭代次数增加,收敛不再变化,模块划分不再改变;在只设置一个精英解时候,收敛模块划分为:5,0,0,6,6,6,6,9,8,8;在设置两个精英解时,收敛模块划分为6,9,9,0,0,0,0,5,1,1;在设置三个精英解时,收敛模块划分为:9,6,6,7,7,7,7,0,3,3;3,7,7,9,9,9,9,6,4,4。结论表示T1为单独模块,T2、T3为同一模块,T4、T5、T6和T7为同一模块,T8为单独模块,T9、T10为同一模块。实验所得的结果刚好符合减速器当前成熟的模块设计标准,说明了方法的可行性和合理性。与现有文献对比,本文研究了绿色模块划分过程中含有模糊数和区间数等定性变量的模型,基于二进制离散粒子群,提出一种十进制离散多目标粒子群算法,尤其和文献[13]比较,本文的研究有几点特色:①解的求解是引入pareto非支配概念的,在多目标求解方法上要优于传统的加权系数法;②本文考虑三角模糊变量的同时,还考虑了区间数的定性和确定化方法,更具有实际生产意义;③本方法非单一解,可能解会呈多样性。
4总结
基于离散二进制上改进获得离散十进制多目标粒子群优化方法,对当前减速器成熟的模块划分进行验证,实例说明了该方法所建立模型及其求解原理的可行性,可以帮助中小企业进行协同设计任务的模块划分,具有非常好的实用参考价值。实验方法收敛速度快,用sigmoid函数来得到的十进制数,由于sigmoid函数本身图形的特性,可能会引起十进制数取值比较集中在某些数值,从而出现收敛较早和局部收敛的情况,增强粒子的扰动性和突破十进制数取值的局限将是作者下一步的研究方向。
[参考文献]
[1] 袁群超,贾瑞通,刘兵兵,等.汽车制造业模块化可配置BOM研究[J].制造业自动化,2013,35(4):6-9.
[2] 刘飞,曹华军,何乃军.绿色制造的研究现状与发展趋势[J].中国机械工程,2000,11(1-2):105-110.
[3] 王日君,张进生,葛培琪,等.模块化设计中模块划分方法的研究[J].组合机床与自动化加工技术,2008,12(7):17-21.
[4] 陆长明,陈 峰,邓劲莲.绿色性对模块化产品设计的影响[J].机械设计与研究,2006,22(6):13-16.
[5] 李婷婷,龚京忠,李国喜,等.可维修性驱动的模块划分[J].机械设计与制造.2007,45(2):166-168.
[6] Tseng H E, Chang C C, Li J D. Modular design to support green life-cycle engineering[J].Expert Systems with Applications, 2008,34(4):2524-2537.
[7] 郭卫,刘光复,张雷.面向全生命周期的产品绿色模块划分方法研究[J].合肥工业大学学报(自然科学版),2010,33(10):1441-1445,1449.
[8] Smith S, Yen C C. Green product design through product modularization using atomic theory [J].Robotics and Computer Integrated Manufacturing,2010,26(6):790-798.
[9] 陈小斌.机电产品绿色模块划分方法研究与应用[D].杭州:浙江大学机械工程学系,2012
[10] Ji Y J, Jiao R J, Chen L, et al. Green modular design for material efficiency: a leader-follower joint optimization model[J],Journal of Cleaner production, 2013, 41(2):187-201.
[11] 唐文献,吴春艳,马宝,等.基于模糊聚类分析的锚绞机模块划分方法研究[J].机械设计, 2012,29(10):24-28.
[12] 徐敬华,张树有.基于多域互用的数控机床模块化配置设计[J].机械工程学报,2011,47(17):127-133.
[13] 刘电霆.绿色设计中产品模块划分的不确定优化及GA求解[J].桂林理工大学学报,2013,33(4):743-748.
[14] 冉静学.三角模糊数排序方法的研究[J].中央民族大学学报(自然科学版),2011,20(4):37-42.
[15] 王新端.基于区间数的不确定优化理论及求解方法研究[D].西安:长安大学应用数学系,2012:29-32.
[16] 李兰,改进的离散粒子群算法求解0_1背包问题[D].广州:华南理工大学理学院,2011.
[17] Vilfredo pareto. Cours D’Economie politique[M]. volume I and II. F. Rouge, Lansanne,1896.
[18] 贾庭芳,基于粒子群优化的离散多目标优化算法[D].太原:太原科技大学机械电子工程,2011.
[19] 唐涛,刘志峰,刘光复,等.绿色模块设计方法研究[J].机械工程学报,2003,39(11):149-154.
(编辑李秀敏)
THDMOpSO Green Reducer Module Based on Uncertain Optimization
LIU Dian-tinga,ZHANG Quan-yongb
(a.College of Mechanical and Control Engineering;b.College of Information Science and Engineering, Guilin University of Technology , Guilin Guangxi 541004,China)
Abstract:Aiming at the problems with variable or parameter uncertainty of green product design, a reducer modular green configuration design as an example, as a variable into interval number and fuzzy number, the green design of product module partition problem with uncertain factors, the module division principle and the main steps in the module, internal polymerization between the degree of maximum, minimum and module partition module coupling degree of the green degree is highest for the multiple objective function, a green product module partition of uncertainty optimization model, the interval number and triangle fuzzy number determination, put forward THDMOpSO method, verified the structure of the reducer module structure is reasonable and effective, feasible and the utility value of production.
Key words:uncertain optimization;green design;modular design;decimal discrete multi-objective particle swarm algorithm
中图分类号:TH122;TG506
文献标识码:A
作者简介:刘电霆(1966—),男,江西吉安人,桂林理工大学教授,博士,研究方向为机械制造及其自动化;通讯作者:张全永(1992—),男,安徽亳州人,桂林理工大学硕士研究生,(E-mail)1370006407@qq.com。
*基金项目:国家自然科学基金项目(51265008);广西自然科学基金项目(2012GXNSFAA053193);广西汽车零部件与整车技术重点实验室项目(2013KFMS10);研究生创新项目(YCSZ2014153);广西科学研究与技术开发计划项目(桂科攻1598007-15)
收稿日期:2015-03-13;修回日期:2015-03-16
