基于时间支撑区域累积的多分量信号识别*

刘歌，张国毅，于岩，胡鑫磊

(空军航空大学 信息对抗系，吉林 长春 130022)

探测跟踪技术

基于时间支撑区域累积的多分量信号识别*

刘歌，张国毅，于岩，胡鑫磊

(空军航空大学 信息对抗系，吉林 长春 130022)

为了将单分量信号和多分量信号有效区分开来，提出了一种多分量信号识别的新方法。首先对信号进行时频变换，并根据一定的规则将时频平面划分为多个时间支撑区域，然后对每一支撑区域沿时间轴进行累积，得到累积频谱图，最后通过统计频谱图上峰值的个数，判定是否为多分量信号。仿真实验表明，该方法能够在低信噪比下有效地将多分量信号识别出来。

雷达侦察；信号识别；多分量信号；时频变换；时间支撑区域；频谱图

0 引言

随着电子战环境中信号密度不断增加和雷达体制越来越复杂，密集的脉冲信号往往同时或相继到达接收机，这些脉冲信号重叠或交叠在一起，形成多分量信号[1]。多分量信号处理是现代电子侦察系统不可避免的问题，准确地识别这些多分量信号对于雷达情报分析具有重要的意义[2]。

由于多分量信号在时域、频域甚至是时频域发生交叠，仅从时域或频域无法对多分量信号进行识别，因此对多分量信号进行处理，一般都在时频域上进行。文献[3-6]采用改进的时频分析方法研究了LFM信号构成的多分量信号，但是实际信号中不仅仅只有LFM信号，所以这些方法不具有普遍使用价值，对其他的多分量信号较难处理；文献[7-8]运用图像处理的技术对多分量辐射源信号的时频图进行处理，但仅限于图像质量的改善，而且在低信噪比的情况下不适用；文献[9-10]能对多分量雷达辐射源信号进行有效的检测与分离，但只针对时频域不交叠的多分量信号。

针对以上问题，为了能够有效识别多分量信号，同时为后续的多分量信号的分离以及参数估计奠定基础，本文提出了多分量信号识别的新方法。首先对多分量信号的时频平面进行区域划分，再沿时间轴分别对每一区域进行累积以便抑制噪声的影响，然后对得到的累积频谱图进行峰值检测，根据峰值个数实现对多分量信号的识别。考虑到采用上述方法可能会将频率编码信号(FSK)误识别为多分量信号，因此需要将混入多分量信号中的FSK信号剔除。仿真实验表明，本文算法能够将多分量信号与单分量信号有效区分开，且具有良好的抗噪性能。

1 多分量信号模型与时频分析

1.1 多分量信号模型

在雷达电子情报侦察系统的接收端，存在着同时到达多个脉冲信号的情况，它们在时域交叠或者重叠，在频域交叠或相邻，这些相互交叠的脉冲信号就构成了雷达多分量信号[11]。构成信号的每一个分量被认为一个单分量信号，以下为多分量信号的具体数学表达式[12]

(1)

(2)

ui(t)=Ai(t)rect(t/Tpi)ej[θi(t)+φi ],

(3)

式中：L为单分量信号的个数，满足L≥2；rect (t)为矩形窗函数；si(t)为第i个单分量信号；ui(t)为信号si(t)的基带信号；Tai，Ni，fci，Tpi，Tri，φi分别为信号的到达时间、脉冲个数、载频、脉冲重复周期、脉冲宽度、初相；θi(t)为信号的相位函数，决定信号的调制类型；Ai(t)为幅度函数；ω(t)为高斯白噪声。

1.2 多分量信号的时频分析

由于本文的分析对象为多分量信号，为了不在时频平面上产生交叉项，因此需要采用线性时频变换对信号进行分析[13]。所以本文选择的时频变换方法为短时傅里叶变换(STFT)，多分量信号x(t)的STFT离散形式定义[14]为

(4)

式中：M为窗函数h(t)的长度。其中窗函数h(t)以及长度M的取值会对STFT的分辨力产生一定影响，因此可以根据具体需要选择合适的窗函数[15]。

对2个线性调频信号(LFM)和一个非线性调频信号(NLFM)构成的多分量信号进行STFT，得到时频图如图1所示，此时信噪比为0 dB。

图1 多分量信号的STFT平面Fig.1 STFT plane of multi-component signal

从图1中不难发现，多分量信号的STFT为各分量STFT的和，不会产生交叉项，此时质量较高的时频平面为后续利用时频平面进行多分量信号识别的过程打下了良好的基础。

2 多分量信号的识别原理

本文研究的多分量信号包括在时域和频域产生交叠的情况，对于这类信号只能在时频域进行识别处理。尽管在全局时间内信号频率会交叠在一起，但是局部时间内各分量间的频率却是可分的。而时频平面的每一时间点对应的序列表示信号在此时间点的瞬时频率，因此本文对信号时频平面进行区域划分，并对每一区域沿时间轴进行累积，不仅能够得到该区域的频谱，也能够有效抑制噪声的影响，通过检测累积频谱图的峰值个数进行多分量信号的识别。该方法也适用于频域不交叠的多分量信号。

2.1 基于时间支撑区域的时频平面划分

为了表述方便，本文引入了时间支撑区域的概念，时间支撑区域Ii(i=1,2,…,k)可以看作是时频平面沿时间轴划分的子平面。对图1中的时频平面进行区域划分如图2所示。

图2 多分量信号时频平面划分时间支撑区域示意图Fig.2 Sketch map of the time-frequency plane divided into time supporting regions

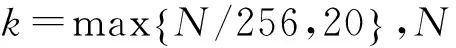
2.2 基于时间累积的谱峰个数检测

只要多分量信号不完全重叠，总是存在时间支撑区域内信号的频率可分离，因此对时间支撑区域内信号的时频序列沿时间轴进行累积，不仅能够得到多分量信号在该段支撑区域内的频谱，而且由于噪声在整个时频平面内是分散的，累积之后噪声能量会明显弱于信号的能量，从而有效抑制噪声对多分量信号识别的影响。之后，统计累积频谱图中峰值的个数，当有M个频谱图出现多个峰值，就可以判断为多分量信号。

M需要根据实际情况选取，本文设置为3。峰值检测时以最大峰值的0.7倍作为门限，超过门限的连续区域判为一个峰值，若检测到峰值数大于1且峰值间的频率差超过设定的差值，则判为多个峰值。

图3中的a)和b)分别为对图2所示的时频平面的第一段时间支撑区域I1和最后一段时间支撑区域I10进行累积得到的频谱图，此时k的取值为10。

从图3中可以看出，支撑区域内累积频谱图中明显存在多个谱峰，且噪声造成的频谱波动很小，不会对谱峰检测造成影响。

图3 时间支撑区域累积频谱图Fig.3 Cumulative spectrograms of time supported areas

图4 累积频谱图峰值分叉现象Fig.4 Peak bifurcation phenomenon of cumulative spectrograms

2.3 多分量信号与频率编码(FSK)信号的识别

本文利用时频平面时间支撑区域沿时间轴累积得到的频谱图进行谱峰检测来识别单分量和多分量信号，如图5所示， 以4FSK信号为例， 它在4个不同的频率上都有分布，所以其时间支撑区域累积频谱图也会出现多个峰值，采用本文方法必然会将FSK信号误识别为多分量信号，因此必须利用其他方法将混入多分量信号中的FSK信号剔除。根据以上分析，本文提取每一时间支撑区域的起始时频序列，并统计每一序列峰值个数，从而识别FSK信号和多分量信号。

根据以上分析，对FSK信号和多分量信号的识别方法如下：

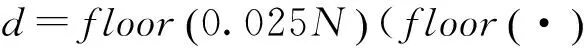
(3) 判断峰值的个数超过2的连续时频序列个数m，若m≥3就判定为多分量信号，否则判定为FSK信号。

2.4 多分量信号识别流程

综上所述，多分量与单分量信号的识别流程如图6所示。具体步骤如下：

(1) 对信号进行STFT，得到信号的时频平面；

图5 4FSK信号提取时间支撑区域起始时频序列示意图Fig.5 Sketch map of extracting time supporting regions starting time-frequency sequence of 4FSK signals

(3) 对各支撑区域沿时间轴进行累积得到频谱图。对累积频谱图进行谱峰个数检测，设置最大峰值的0.7倍作为门限th1，搜索大于门限th1的峰值个数。如果2个峰值之间的间隔在一定的范围内，将2个峰值判为一个峰值，本文选取的间隔为floor(0.025N)；

(4) 判断有多个谱峰的频谱图的个数n。若n≥M，就可以判断为多分量信号，并执行下一步，本文设置M=3。否则判定为单分量信号；

(5) 对(4)中识别为多分量的信号进行进一步的识别。具体步骤见2.3，将可能误识别为多分量信号的FSK信号识别出来。

3 仿真实验

由于多分量信号的组合形式难以确定，因此本文将单分量信号的误识别率作为本文识别方法的性能指标。选取LFM，NLFM，FSK，BPSK，MPSK 5类常见的单分量信号，仿真实验在Matlab 2012a环境下进行。仿真条件如下：各分量的采样点为1 024；LFM和NLFM信号的归一化起始频率和终止频率都分别设置为0.1和0.3，NLFM选用正弦调制类型；FSK，BPSK以及MPSK信号的码长都设置为64，其中FSK信号选取2FSK和4FSK，编码频率在[0,0.5]内随机选取；BPSK信号采用13位巴克码，归一化载频设置为0.25； MPSK信号以P3码和P4码为例，归一化载频都为0.25。文中涉及到的阈值，已在相应位置进行了说明。噪声采用高斯白噪声。在-8～5 dB的信噪比范围内，每隔1 dB对各单分量信号作500次Monte Carlo实验。

图6 多分量与单分量信号的识别流程Fig.6 Flow chart of the identification of multi-component signal and single component signal

图7给出了7种单分量信号识别为多分量信号的误识别率。

图7 单分量信号的误识别率Fig.7 Error probability in recognizing of single component signals

从图7可以看出，单分量信号的平均误识别率在信噪比为-5 dB时达到20%以下，在信噪比为0 dB时达到1%以下。随着信噪比的升高，单分量信号识别为多信号的误识别率会减小。从每类信号具体来看，FSK信号的误识别率高于其他信号，这是因为在提取时间支撑区域起始时频序列的过程中，会受到噪声以及码元边缘效应的影响，导致峰值个数检测不准，从而使FSK误识别为多分量信号；对于MPSK信号，尽管在时频平面上会存在主脊线和副脊线，但是由于脊线能量分布的原因，在对时间支撑区域进行累积时，峰值多于2个的累积频谱图个数没有超过M，因此误识别率较低。对于其他3类信号，误识别率相差不大。在信噪比低于-5 dB时，噪声的能量升高，从而淹没信号能量较低的部分，在对时间支撑区域进行累积时，噪声能量可能累积成峰值，导致无法正确判断峰值的个数，因此误识别率升高。

4 结束语

本文提出的多分量信号的识别方法，是利用时间支撑区域沿时间轴进行累积得到的累积频谱图上峰值的个数区分多分量信号和单分量信号，并利用时间支撑区域起始时频序列的峰值个数剔除混入多分量信号的FSK信号。仿真实验表明，在信噪比为-1 dB时单分量信号的平均误识别率达到1%以下，说明本文的识别方法具有较强的抗噪性能。且本文方法原理简单，易于实现，具有较为重要的应用价值。

[1] 荣海娜, 张葛祥, 金炜东. 多分量雷达辐射源信号检测新方法[J]. 系统工程与电子技术, 2009, 31(9): 2096-2010. RONG Hai-na, ZHANG Ge-xiang, JIN Wei-dong. Novel Detection Method for Multi-Component Radar Emitter Signals[J]. Systems Engineering and Electronics, 2009, 31(9): 2096-2010.

[2] 李亚军. 多分量雷达辐射源信号检测技术研究[D].哈尔滨：哈尔滨工程大学, 2011: 1-15. LI Ya-jun. The Research on Detection Technology for Multicomponent Radar Emitter Signals[D]. Harbin:Harbin Engineering University, 2011: 1-15.

[3] 李楠, 曲长文, 平殿发, 等. 基于时频重排与WHT的多分量LFM信号识别[J]. 航天电子对抗, 2009, 25(6): 33-36. LI Nan, QU Chang-wen, PING Dian-fa, et al. Multicomponents LFM Signal Recognition Based on Time-Frequency Reassignment and Wigner-Hough Transform[J]. Aerospace Electronic Warfare, 2009, 25(6): 33-36.

[4] 程柏林, 马晓岩, 陈蓓. 基于时频重排多分量辐射源信号分析研究[J].系统工程与电子技术, 2006, 28(5): 684-686. CHENG Bo-lin, MA Xiao-yan, CHEN Bei. Analysis of Multi-Component Radiator Signal Based on Time-Frequency Reassignment Method[J]. Systems Engineering and Electronics, 2006, 28(5): 684-686.

[5] PHAM D S, ZOUBIR A M. Analysis of Multicomponent Polynomial Phase Signals[J].IEEE Trans. on Signal Processing, 2007, 55 (1):56-65.

[6] 王军, 李亚安. 多分量信号时频分析交叉项抑制研究[J], 探测与控制学报, 2004, 26(4): 13-17. WANG Jun, LI Ya-an. The Research of Cross-Component Suppression of Multicomponent Signals Using Time Frequency Analysis[J]. Journal of Detection and Control, 2004, 26(4): 13-17.

[7] 邹兴文, 张葛祥. 基于图像处理技术的雷达辐射源信号时频特性分析[J]. 电路与系统学报, 2009, 14(3): 135-140. ZOU Xing-wen, ZHANG Ge-xiang. Time-Frequency Analysis of Radar Emitter Signals Based on Image Processing Technology[J]. Journal of Circuits and Systems, 2009, 14(3): 135-140.

[8] 程柏林，陈蓓，赵国林. 一种多分量LFM信号脉内调制特征的提取方法[J]. 电子信息对抗技术, 2006, 21(3): 11-15. CHENG Bo-lin, CHEN Bei, ZHAO Guo-lin. A Method for Extraction of Intra-Pulse-Modulation Characteristics of Multicomponent LFM Signal[J]. Electronic Information Warfare, 2006, 21(3): 11-15.

[9] 刘勇, 张国毅, 齐兴龙, 等. 多分量雷达辐射源信号的检测与分离[J]. 航天电子对抗, 2014, 30(3): 37-41. LIU Yong, ZHANG Guo-yi, QI Xing-long, et al. Detection and Separation of Multi-Component Radar Emitter Signals[J]. Aerospace Electronic Warfare, 2014, 30 (3): 37-41.

[10] 荣海娜. 多分量雷达辐射源信号模型和检测估计算法研究[D]. 成都: 西南交通大学, 2010: 25-29. RONG Hai-na. Models and Detection Estimation Algorithms for Multicomponent Radar Emitter Signals[D]. Chengdu: Southwest Jiaotong University, 2010: 25-29.

[11] 蔡权伟. 多分量信号的信号分量分离技术研究[D]. 成都: 电子科技大学, 2006: 34-36. CAI Quan-wei. Research on Separation of Signal Components of Multicomponent Signal[D]. Chengdu: University of Electronic Science and Technology of China, 2006: 34-36.

[12] 史文国, 徐向辉. 基于分数阶傅里叶变换的多分量线性调频信号检测和参数估计的快速自适应方法[J]. 科学技术与工程, 2012, 20(7): 1517-1521. SHI Wen-guo, XU Xiang-hui. Fast Adaptive Method of the Multi-LFM Signal Detection and Parameter Estimation Based on Fractional Fourier Transform[J]. Science Technology and Engineering, 2012, 20(7): 1517-1521.

[13] WANG Jin-zhen, SU Shao-ying, CHEN Zeng-ping. Parameter Estimation of Chirp Signal Under Low SNR[J]. Science China：Information Sciences, 2015, 58(2): 79-91.

[14] 李仙. 非平稳信号的时频变换研究[D]. 西安: 西安工业大学, 2014: 34-36. LI Xian. Research on Time-Frequency Transform in Nonstationary Signal[D]. Xi’an: Xi’an Technological University, 2014: 34-36.

[15] 张贤达, 保铮. 非平稳信号分析与处理[M]. 北京:国防工业出版社, 1998. ZHANG Xian-da, BAO Zheng. Nonstationary Signals Analyzing and Processing[M]. Beijing: National Defence Industry Press, 1998.

Multi-Component Signal Recognition Based on Cumulative Time Supporting Region

LIU Ge, ZHANG Guo-yi, YU Yan, HU Xin-lei

(Aviation University of Air Force，Department of Information Countermeasures, Jilin Changchun 130022, China)

To distinguish the multi-component signals and single component signals effectively, a new method for multi-component signal recognition is presented. Firstly, the signal is processed by time-frequency transform.Then the time-frequency plane is divided into several time supporting areas according to certain rules. After that, the support regions are cumulated along the time axis respectively to obtain the cumulative spectrum. Finally, the number of spectrum peaks is counted to determine whether the signal is the multi-component signal. Simulation results show that this method has a good anti-noise performance.

radar reconnaissance; signal identification; multi-component signal; time-frequency transform; time supporting region; spectrogram

2015-11-30；

2016-03-18

刘歌(1991-)，女，山东威海人。硕士生，主要研究方向为复杂调制雷达信号的处理。

10.3969/j.issn.1009-086x.2016.06.019

TN959;TN971.1;TP391.9

A

1009-086X(2016)-06-0109-06

通信地址：130022 吉林省长春市南湖大路2222号空军航空大学11队

E-mail：yyliuge@sina.com