基于时序主成分分析的捷联惯组稳定性评估*

陈建春，甄占昌，徐军辉，高岩峰

(火箭军工程大学，陕西 西安 710025)

测试、发控技术

基于时序主成分分析的捷联惯组稳定性评估*

陈建春，甄占昌，徐军辉，高岩峰

(火箭军工程大学，陕西 西安 710025)

针对捷联惯组稳定性评估研究中，缺少客观的评估模型，不能深入的刻画出捷联惯组在使用过程中稳定性变化规律和不能很好确定稳定性较差的误差系数。提出利用时序主成分分析法，建立一个综合评价模型，结合惯组的履历信息和历次测试数据，对惯组稳定性进行评估。实例分析表明，综合模型能够较好描述惯组稳定性变化，特别是反映惯组稳定性有异常变化的情况；并从主成分综合影响度的角度，确定惯组稳定性较差的误差系数。

捷联惯组；稳定性评估；时序主成分；评估模型；综合评价指标；异常变化

0 引言

近年来，捷联惯组已经广泛应用于航空航天领域。捷联惯组稳定性指标是重要的作战指标要求，通过对惯组的稳定性进行评估，做出科学的使用决策，是一种提高惯组使用性能的切实有效的方法。目前，使用单位一般都是利用射前标定结果，也就是单次通电特性来评估惯组的性能，这种方法虽然有效，但是导致惯组的使用率很低；有部分学者提出利用经典统计学方法，结合惯组的履历信息，对同批次多套惯组的历次测试数据进行统计分析，在此基础上评估惯组的性能，这种方法虽然能够大致判断批次惯组的稳定状况，但是需要大量惯组作为统计样本，并且没有建立合理的评估模型、缺少对单套惯组的性能研究，无法在实际使用中优选惯组[1]。考虑到以上问题，本文在惯组的历次测试数据和履历信息基础上，着眼于惯组常用误差系数，利用时序主成分分析法，研究建立一个能揭示惯组稳定性变化又符合客观历史的评估模型，同时确定稳定性较差的误差系数，克服单纯利用射前标定结果评估惯组性能片面性和主观随意性，揭示惯组性能变化过程。该方法为研究惯组的稳定期提供一定的基础；可较好的评估惯组的实际性能，给实际使用中优选惯组提供一定的理论依据；根据误差系数稳定性不同，优化标定测试方案，提高测试效率等多方面工程应用价值[2]。

1 时序主成分分析法

时序主成分分析法是时序分析和主成分分析方法的结合,在主成分分析的基础上，以一个综合变量来取代原有的全局变量，以此为基础描绘出系统的总体水平随时间的变化轨迹[3]。

1.1 时序主成分分析法原理

时序主成分分析法是主成分分析的时间序列化。基本思想是，伴随相关变动的p个随机变量:x1，x2，…，xp的背后，有比较少的q个不可观测的彼此互不相关的且包含原有指标大多数信息量共同变动因素存在。这q个不可观察的共同因素就是我们所要寻找的主成分，随后再对这组新指标进行时序分析，即根据它们对样本总量的贡献度赋予权数，构造出一组综合指标，以此来量化的反映出对象的发展态势[4]。最后根据各时间段的综合指标值作时序图，这样就形成了能反映研究对象动态轨迹的时间序列图。这样我们通过寻求变量的基本结构，简化了观测系统，即达到减少变量维数、用一个变量子集来解释整个问题。因此通过时序全局主成分分析就可得到统一的主成分公共因子，能迅速提取立体表的重要信息,从而对样本进行评价分析，这样就可以从全局的角度观察和分析数据系统主要因素的动态变化规律[5-6]。

其基本原理可以用一下数学推理过程表示出来：设n个样品，每个样品观测P项指标(变量)：X1，X2，…,Xp得到原始数据资料[3]：

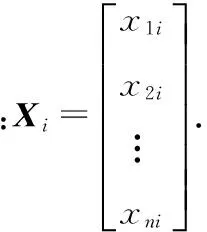
用数据矩阵X的p个向量(即P个指标向量)：X1，X2，… ，Xp作为线性组合(即综合指标向量)为

式中：Xi，Yi均为n维向量，且有：

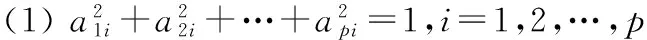
(2)Yi与Yj(i≠j；i，j=1,2,…，n)不相关，Y1是X1，X2，X3，…，Xp的所有线性组合中方差最大者，Y2是与Y1不相关的X1，X2，X3，…,Xp的所有线性组合中方差最大者，Yn是与Y1，Y2，…,Yn-1不相关的X1，X2，…，Xp的所有线性组合中方差最大者。

由以上方法确定的新变量指标Y1，Y2,…,Yn称为原变量指标X1，X2,…,Xp的第1，第2，… ，第n主成分。其中Y1在总方差中所占的比例最大，Y2,…,Yn的方差依次递减。

1.2 时序主成分分析方法计算步骤

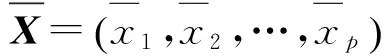
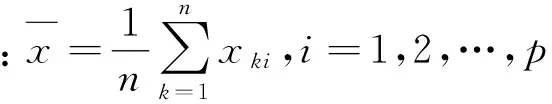
并按下式进行标准化：

式中：xij为第i个指标的第j个分区的原始数据。该式可运用Matalab软件中mean函数和std函数,直接求解。

R=(rij)n×p,

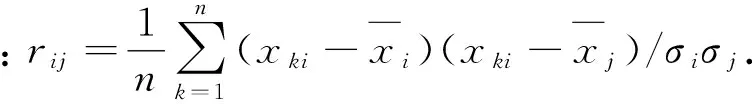
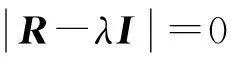
(1)

式中：F为综合指标，代入主成分分析结果，可以得到综合评价值。

(7) 绘制综合评价指标F时间序列图[11-12]。时序分析是借助图像法,通过直接观察数据点的相对位置的变化,分析数据的运动规律及其结构变迁。

2 应用实例

下面以某批次履历相同的3套惯组为例，利用时序主成分法，分析惯组稳定性变化，并确定稳定性较差的误差系数。为保证主成分分析的科学性和数据统计工作的简化，现取这3套惯组各自装备后3年内33个常用误差系数的11次测试数据(其中2006年3次，2007年5次，2008年3次)进行主成分分析。下文主要以惯组1展现主成分分析过程，表1为惯组1的历次测试数据。

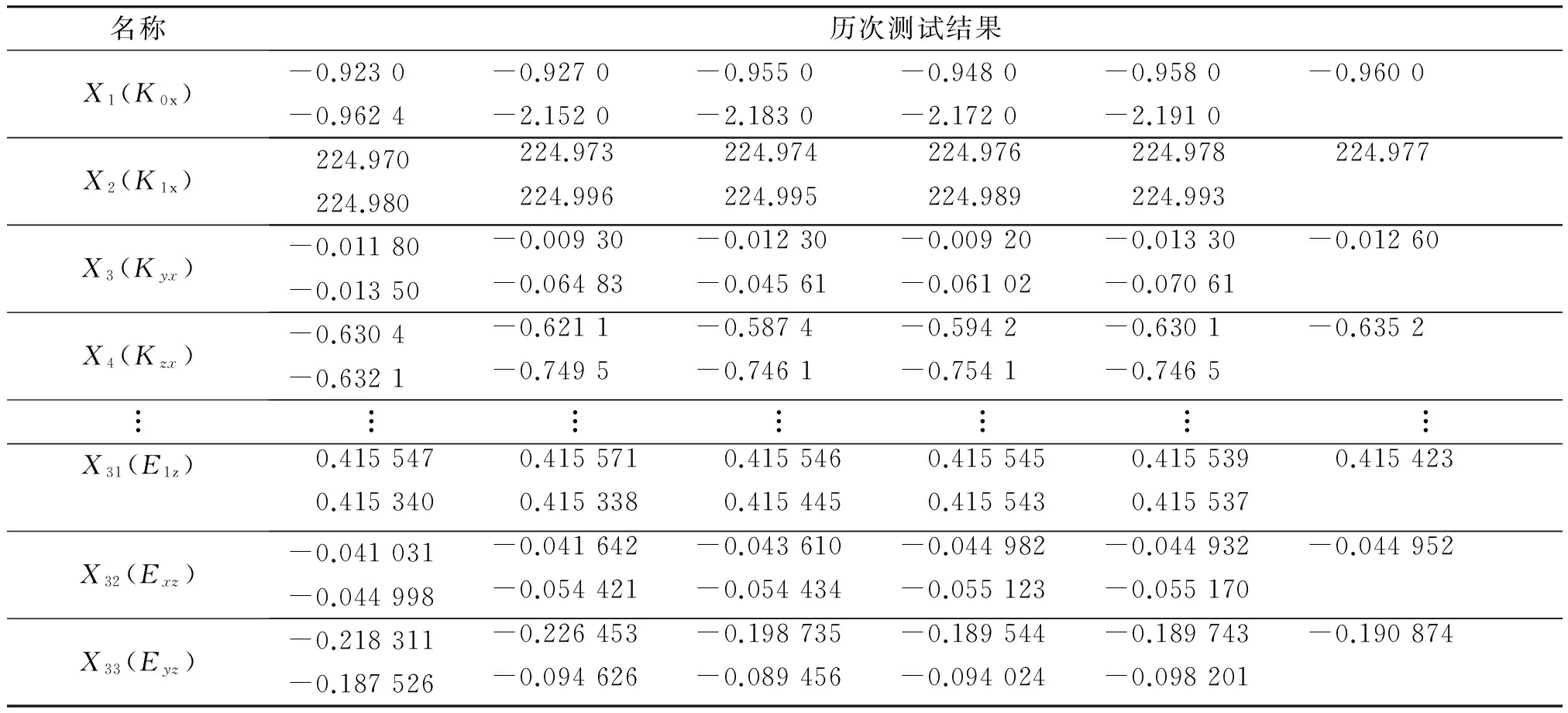
表1 惯组1历次测试数据(简表)Table 1 Previous test data of IMU1

注：K0x为纵向加速度计Ax的偏置；K1x为纵向加速度计Ax的脉冲当量；Kyx,Kzx分别为法向加速度计的安装误差系数；E1z为陀螺仪z通道脉冲当量；Exz,Eyz为陀螺仪z通道安装误差系数。该表省略的26个误差系数依次是K0y～Kzy，K0z～Kyz；陀螺通道漂移系数D0x～D3x，D0y～D3y，D0z～D3z；脉冲当量E1x,E1y；陀螺仪通道安装误差系数Eyx，Ezx,Exy,Ezy。

2.1 主成分分析

对历次测试数据按照图1流程运用Matlab进行分析，得到主成分负荷阵如表2(仅列举惯组1)。

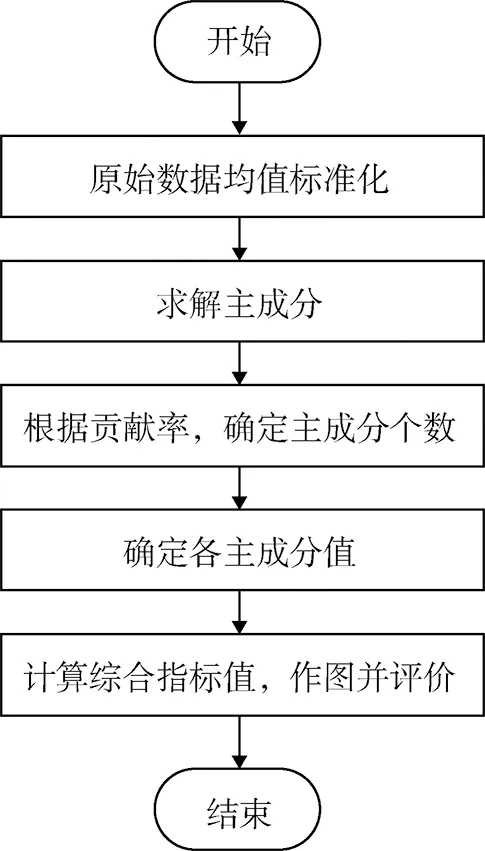
图1 运用时序PCA进行惯组稳定性评估流程图Fig.1 Flow chart of apply Ts-PCA in stability assessment

通过以上分析可以得出累计贡献率在第5主成分时达到90.187%，满足主成分累计贡献率达到85%的要求，因此取前5个主成分即可，根据主成分负荷阵可得5个主成分代替原来的33个误差系数。

由式(1)和表2，构造惯组稳定性综合评估模型，可得惯组1综合评价指标

相同方法可得惯组2，3的综合评价指标

F2=0.44X30+0.35X1+0.33X9+0.33X2+0.26X6+ 0.24X5+0.24X10+0.07X7+0.05X14+…,F3=0.41X10+0.36X30+0.35X2+0.34X1+0.27X9+ 0.27X5+0.24X9+0.1X7+….

2.2 惯组稳定性评估

将历次测试数据标准化后代入综合评估模型，得到3套惯组综合评价指标F各时间的值，作F的时间序列图，如图2。

从时间序列图中可以看出，综合评价指标F的趋势是随着时间逐渐变大，变化比较稳定，结合惯组履历信息，对惯组稳定性进行分析，发现惯组的稳定性是随着工作时间变长逐渐变差，这种变化是较为缓慢且较稳定的；在2007年11月(第8次测试)，3套惯组F值都发生较大波动，然后又趋于稳定的变化，分析发生变化的原因，发现在这次测试之前系统经过了转场，惯组经历了一次长途运输，所以惯组稳定性发生较大变化，这可能是惯组在运输过程中受到力矩作用和路面不平因素影响，以及长途运输前后两地重力加速度变化。由此，可认为惯组在相对静止的条件下稳定性会逐渐变差，性能有所退化，但变化较慢且规律；在经过长途运输等特殊情况后，则稳定性会大幅变差。

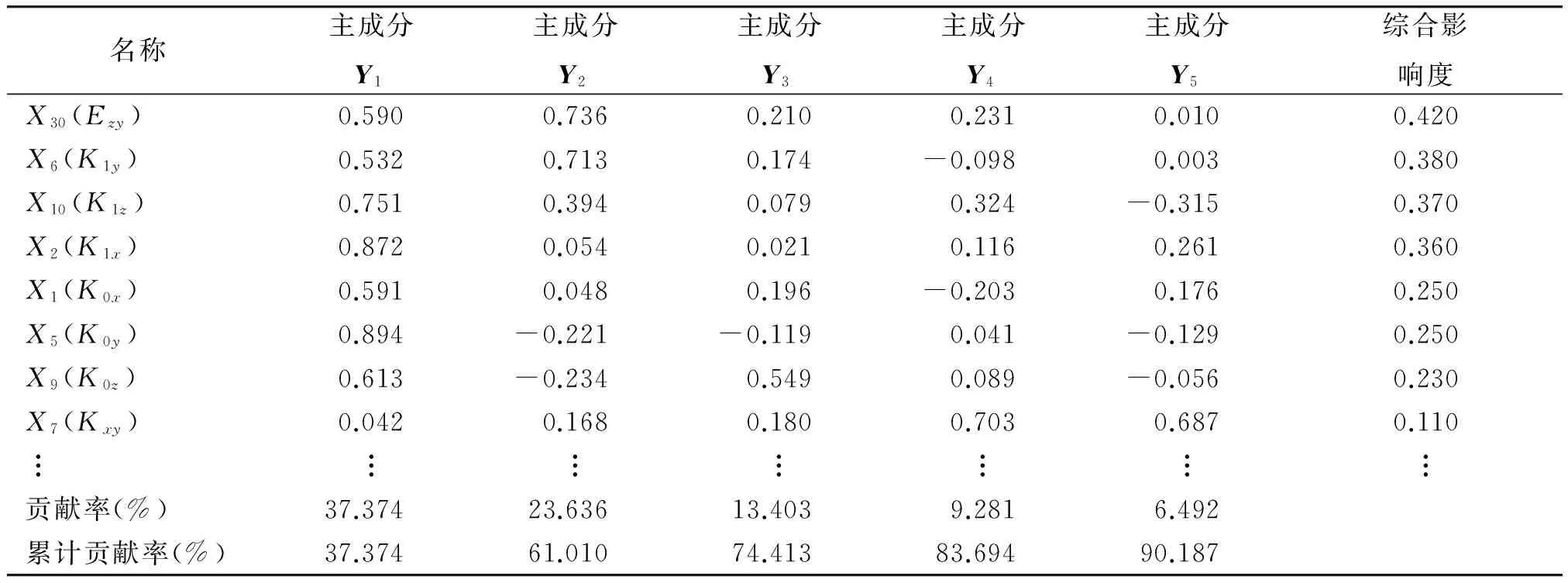
表2 主成分负荷阵(惯组1)

注：综合影响度是综合评估指标中各变量X的系数，省略了综合影响度(<0.05)较小变量。

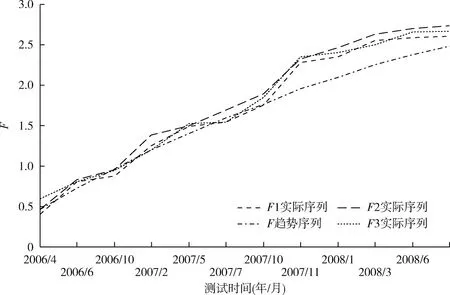
图2 综合指标F时序图Fig.2 Time-series diagram of comprehensive index F

同时，从综合模型中(变量X的系数)得到X1，X2，…，X33的综合影响度，即惯组各个误差系数的稳定性变化的程度，不难看出，3套惯组的加速度计纵向、法向、横向偏置(K0x，K0y,K0z)；加速度计纵向、法向、横向脉冲当量(K1x，K1y，K1z)；加速度计安装误差系数(Kxy)；陀螺仪安装误差系数(Ezy)，这8个误差系数在F1，F2，F3中得分虽然有一定差异，但较其他误差系数得分大很多，另外还发现惯组2的陀螺仪一次项漂移系数(D1X)也得分较高，说明这些误差系数对惯组总体稳定性影响较大，也就是它们稳定性较差；同时也说明同批次惯组的性能是很相近的[13-15]。以上分析结果与文献1中的利用传统统计方法得到的批次惯组性能相吻合，通过对其他批次多套惯组应用相同方法进行分析，发现能够得到相同结论。

3 结束语

本文在大量惯组历次测试数据的基础上，运用时序主成分分析法，建立综合评估模型，描述惯组稳定性变化轨迹，评估惯组性能，确定惯组稳定性较差的误差系数。实例分析可以看出，时序主成分方法在保留原始数据信息的基础上，实现了数据降维，利用提取出的主成分构建新的惯组稳定性综合评估模型，描述惯组稳定性变化，特别是在惯组经过运输后综合评估指标F发生异常变化，这表明该综合评估模型能较好评估惯组性能，另外，通过计算各个误差系数的综合影响度，提取出稳定性较差误差系数。分析结果表明这是一种科学的惯组稳定性评估方法，为提高惯组使用性能的研究提供了参考[6]。

[1] 徐军辉．捷联惯性测量数据分析方法研究[D] ．西安：第二炮兵工程学院，2003． XU Jun-hui.Analysis Method Study of SIMU Data [D].Xi’an:The Second Artillery Engineering University,2003.

[2] 秦永元．惯性导航[M]．北京：科学出版社，2006． QIN Yong-yuan. Inertial Navigation [M]. Beijing: Science Press, 2006.

[3] Richard A Johnson，Dean W Wichern.实用多元统计分析[M]．陆璇，叶俊,译．北京： 清华大学出版社，2008． Richard A Johnson, Dean W Wichern. Practical Multivariate Statistical Analysis [M]. LU Xuan, YE Jun, Translated. Beijing: Tsinghua University Press, 2008.

[4] 王静龙．多元统计分析[M].北京：科学出版社，2008． WANG Jing-long. Multivariate Statistical Analysis [M] Beijing: Science Press, 2008.

[5] 刘毅，李爱群，丁幼亮，等． 基于时间序列分析的结构损伤特征提取与预警方法[J]． 应用力学学报，2008，25(2)：253-256． LIU Yi, LI Ai-qun, DING You-liang,et al. The Character Collection of Ctructure Injury and Warning Method Based on Ts Analysis[J].Journal of Application Mechanics, 2008,25(2):253-256.

[6] 范建容，张建强，田兵伟，等．汶川地震次生灾害毁坏耕地的遥感快速评估方法[J]．遥感学报，2008，20(6)：917-924． FAN Jian-rong, ZHANG Jian-qiang,TIAN Bing-wei, et al. A Rapid Remote Sensing Evaluation Method of The Destroy to The Plough about Earthquake in Wenchuan[J].Journal of Remote Sensing, 2008,20(6):917-924.

[7] 张永进，岳新利，武晟，等．综合优化模型在洪灾评估中的应用[J] ．系统工程理论与实践，2008，28(9) ：112-116． ZHANG Yong-jin, YUE Xin-li,WU Sheng,et al. Comprehensive Evaluation Model Used in the Flood Assessment[J] . System Engineering Theory and Practice,2008,28(9) :112-116.

[8] 苏键，陈军，何洁．主成分分析法及其应用[J] ．轻工科技，2012，166(9)：12-16． SU Jian, CHEN Jun,HE Jie. Principal Component Analysis and Its Application[J].Light Industry and Technology, 2012,166(9):12-16.

[9] 朱军华，余岭． 基于时间序列分析与高阶统计矩的结构损伤检测[J]． 东南大学学报: 自然科学版，2012，42( 1):137-142． ZHU Jun-hua, YU Ling. Detection of Structure Injury Based on Ts Analysis[J].Journal of Southeast University Natural Science ed, 2012，42(1) :137-142．

[10] LIU X P, WANG J M . Improved ICA Method and Application in Transient Electromagnetic Signal Processing[J]. Journal of Beijing Normal University:Natural Science ed, 2011,47(1):34-39.

[11] 蒋浩，洪丽．主成分分析结合神经网络的光伏发电量预测[J]. 电力系统及其自动化学报,2013,25(6):101-105. JIANG Hao, HONG Li. PV Generation System Forecasting Model Based on Neutral Network and Principal Components Analysis[J].2008,Proceeding of the CSU-EPSA,28(9) :112-116.

[12] 张会会，张伟,胡昌华，等．基于主成分分析法的惯性器件寿命预测[J]. 系统仿真技术,2011,7(4):249-253. ZHANG Hui-hui, ZHANG Wei，HU Chang-hua, Inertia Device Lifetime Prediction Based on Principal Component Analysis[J]. System Simulation Technology, 2011,7(4):249-253.

[13] 刘昊知，胥布工,高福荣，等．基于时序模型迁移的间歇过程建模方法研究[C]∥第25届中国过程控制会议，大连，2014,6. LIU Hao-zhi, XU Bu-gong,GAO Fu-rong, et al. Research on Modeling Method of Monitoring for Batch Process Based on Time Series Model Migration[C]∥The Chinese 25th Conference on Processing Control, Dalian, June,2014.

[14] LIU Zhe, ZHONG Yuan. University of Technology.Super Fuzzy Feature Model for Detection of Materials[C]∥2010 International Conference on Advanced Measurement and Test,May15,2010.

[15] 肖剑．水电机组状态评估及智能诊断方法研究[D].武汉：华中科技大学，2015. XIAO Jian.Performance Degradation Evaluation and Intelligent Fault Diagnosis Hydropower Generator Unit[D]. Wuhan: Centre China Technology University,2015.

[16] 程然，吴海桥．基于模型的飞机级功能危险评估方法研究[J] .飞机设计，2015,35(4)：61-66. CHEN Ran,WU Hai-qiao, Research for Model-Based Functional Hazard Assessment Method at Aircraft Level[J]. Aircraft Design, 2015,35(4)：61-66.

SIMU Stability Evaluation Based on Time-Series Principal Component Analysis

CHEN Jian-chun, ZHEN Zhan-chang, XU Jun-hui, GAO Yan-feng

(The Rocket Force Engineering University,Shaanxi Xi’an 710025, China)

Due to the lack of objective assessment model, the changing of strapdown inertial measurmert unit(SIMU) stability in-depth in work progress cannot be portrayed and the poor stability error coefficients in the stability assessment of SIMU cannot be determined. A comprehensive evaluation model is established by using time-series principal component analysis (Ts-PCA), and IMU resume information and previous test data are combined to evaluate stability of SIMU. Example analysis shows that comprehensive model can describe the SIMU stability change very well, especially the abnormal changes. The error coefficient of the SIMU with poorer stability is determined from the angle of principal component comprehensive effect.

strapdown inertial measurmert unit(SIMU); stability assessment; time-series principal component analysis(Ts-PCA); assessment model; comprehensive evaluation index; abnormal change

2016-01-23；

2016-04-01

中国博士后科学基金(2012M518)

陈建春(1992-)，男，江西丰城人。硕士生，主要从事惯导测试技术研究。

10.3969/j.issn.1009-086x.2016.06.024

V249.32+2

A

1009-086X(2016)-06-0142-06

通信地址：710025 陕西省西安市灞桥区同心路2号火箭军工程大学4502分队

E-mail：18700793820@139.com