临近空间高超声速目标自适应采样跟踪算法*

李凡，毕红葵，段敏，喻晨龙

(1.空军预警学院 研究生管理大队，湖北 武汉 430019； 2．空军预警学院，湖北 武汉 430019)

探测跟踪技术

临近空间高超声速目标自适应采样跟踪算法*

李凡1，毕红葵2，段敏2，喻晨龙1

(1.空军预警学院 研究生管理大队，湖北 武汉 430019； 2．空军预警学院，湖北 武汉 430019)

针对传统自适应采样跟踪准则只适用单一模型且采样率稳定性差的问题，提出一种基于相对机动强度(relative maneuvering strength, RMS)的自适应采样交互多模型(interacting multiple model,IMM)算法。该算法构建了机动灵敏的主导因子；将期望协方差与实际协方差的偏差与门限值进行比较来修正指数参数，在保证跟踪精度恒定的同时降低资源消耗；考虑到采样率稳定性因素，引入平滑因子，设计线性形式自适应采样率公式。通过仿真试验对比，结果表明3种对比算法跟踪精度相近，新算法采样点数少，采样率突变点少。以此验证了新算法在跟踪数据率和采样率稳定性方面的优越性。

临近空间；高超声速目标；自适应采样；相对机动强度；交互多模型；跟踪数据率

0 引言

近年来，临近空间高超声速飞行器(near space hypersonic target, NSHT)屡次发射引起世界各国关注[1]。NSHT具有广阔的军事应用前景，其高、快、小的特点，为进攻性武器的研究与运用开辟了一个新的领域。

目前，高速高机动目标跟踪算法已有较多成果，且主要集中于IMM算法[2]，但是专门针对NSHT的跟踪算法相对较少。文献[3]提出一种IMM算法跟踪NSHT的思路；文献[4]基于IMM算法提出3种变结构多模型(variable structure multiple model, VSMM)算法，通过自适应模型集选取解决模型竞争和计算量的问题。上述算法对于NSHT跟踪有一定的改进效果，但是跟踪采样间隔时间固定，停留在边扫描边跟踪(track while scanning, TWS)的思路上。针对这些问题，基于单个运动模型方面，文献[5-7]分别提出适应匀速(constant velocity, CV)、匀加速(constant acceleration, CA)、Singer模型特点的自适应采样公式，只针对特定模型，采样率稳定性较差，容易出现突变点。基于期望协方差方面，文献[8]提出以期望协方差为参数优化的约束条件，同时调整采样间隔与驻留时间，但发现概率设定较大时会出现多个无效的测量；文献[9]提出协方差偏差均值最小和最大协方差偏差最小准则，合理控制下一时刻搜索、跟踪模式，并提出2种准则评估协方差偏差程度，实现对搜索参数以及跟踪参数优化，但算法假设驻留时间足够大；文献[10]提出使用后验克拉美罗矩阵的迹与门限比较，通过加减固定的时间步进来自适应调整采样间隔，但是算法时间步进确定较为困难，当机动突变时采样率变化较慢、适应性较差；文献[11]提出将灰色关联度引入到以采样间隔为粒子的粒子群优化中，提高跟踪精度的同时减少观测点数达到优化雷达资源管控的目的[12]，但是粒子群很难得到全局最优结果。

本文采取跟踪加搜索(track add search, TAS)[13]方式跟踪NSHT，基于目标机动强度分析，提出一种RMS-IMM自适应采样跟踪算法，实现采样率的自适应调整。该算法从采样率灵敏度和稳定性的角度进行理论分析，设计灵敏的主导因子，通过修正主导因子的指数参数保持跟踪精度恒定，引入平滑因子提高采样率自适应调整过程中稳定性，仿真结果表明RMS-IMM算法机动适应性、采样率稳定性优于传统自适应采样率算法的。

1 IMM算法

IMM算法[14]主要包括多个模型滤波以及模型交互计算2个部分。使用不同的运动模型对系统进行预测，根据马尔可夫链的状态转移矩阵，计算各模型系统的可能性作为权值，对各模型滤波结果进行加权和得到IMM算法的滤波输出。

步骤 1： 模型状态交互输入

(1)

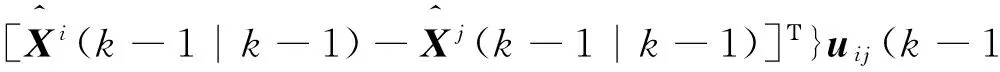
(2)

步骤 2： 模型可能性计算

假定Z(k)为k时刻的量测值，模型j在k时刻的滤波残差为vj(k)，其协方差为Sj(k)，则模型j的可能性为

(3)

(4)

(5)

步骤 3： 模型概率更新

(6)

步骤 4： 交互输出

(7)

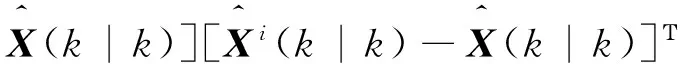
(8)

文献[6]提出CA模型的自适应采样递推公式。目标机动较弱时，跟踪精度趋于稳定，平滑过的位置残差小于观测噪声标准差，导致采样间隔增大，跟踪精度降低，当滤波残差超越量测噪声时，采样间隔会立即降低，出现采样率突变点。CA自适应采样准则对复杂运动的适应性较差。文献[7]基于期望的预测精度和稳态的卡尔曼滤波条件下给出了Singer的自适应变采样公式，式中先验参数较多，受环境噪声影响较大，采样率稳定性较差。上述2种自适应采样准则容易出现采样率突变点、稳定性较差。并且都是针对特定模型，难以运用到IMM算法中。

2 RMS自适应采样准则

针对上述单模型自适应采样准则在IMM算法[14]中的适应性问题，以相邻k-1和k2个时刻残差描述k时刻相对于k-1时刻目标机动强度。构造对机动强度变化反应灵敏的主导因子；通过预测协方差与期望协方差偏差修正指数参数；引入跟踪精度与位置误差调整平滑因子[15]，提高跟踪过程中采样率的稳定性，减少采样率突变点。在实际跟踪过程中往往更加关注目标的位置信息，基于IMM算法滤波加权和的思想，对各模型滤波位置残差加权和作为当前时刻混合位置残差。

(9)

(10)

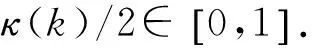
式(10)中，当目标机动较强时，滤波残差增大导致σ2(k)>σ(k-1)σr，采样间隔T(k)减小，采样率增大；当目标机动较弱时σ2(k)<σ(k-1)σr，T(k)增大，采样率减小；当目标近似匀速运动时σ2(k)≈σ(k-1)σr，滤波残差趋于平稳，T(k)变化较小，采样率保持恒定[16-17]，避免出现CA自适应准则在弱机动时采样间隔不断增大的问题。

考虑到算法指数参数κ(k)/2对下一时刻采样间隔影响较大，为实现不同采样时间点跟踪精度维持在一个较为稳定的水平，防止因采样间隔单次调整偏差较大导致后续跟踪精度降低[17]，通过绝对值求积衡量指数参数κ(k)/2下实际协方差与期望协方差偏差[10]:

ΔP(k)=tr‖P(k|k)-Pe‖，

(11)

式中：Pe为期望协方差；ΔP(k)反映当前时刻自适应采样间隔时间调整的准确性，基于ΔP(k)与门限值α比较修正κ(k)/2取值[11]，保证跟踪精度误差在一定范围内。

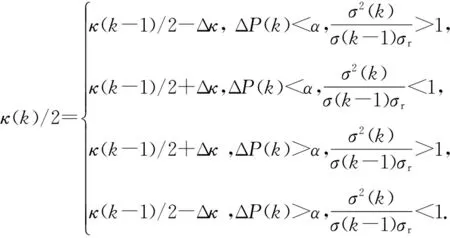
(12)

Δκ为指数参数步进，在不严重影响机动强度分析的同时微调κ(k)/2修正采样间隔。当ΔP(k)小于α时，采样间隔T(k)高于跟踪精度要求，通过参数调整适当增大T(k)，减小计算资源浪费；当ΔP(k)大于α时，T(k)低于跟踪精度要求，减小T(k)增大采样率，降低滤波位置误差防止跟踪失败。

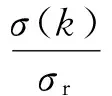
T(k)=βT1(k-1)+(1-β)T2(k-1),

(13)

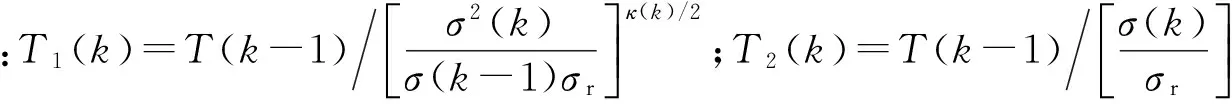
式(13)以平滑系数构建一个线性自适应变采样率公式，兼顾采样率高灵敏性与鲁棒性要求。T1(k)为主导因子，机动强度分析采用指数形式能快速调整下一时刻采样间隔，反映机动强度变化趋势，通过协方差偏差门线比较修正指数参数κ(k)/2，保证跟踪精度稳定。针对指数形式主导因子稳定性较差容易出现采样率突变点的问题，加入平滑因子T2(k)，以线性形式抑制机动突变导致的采样率急剧变化，解决采样率突变的问题[6-7]。

3 仿真验证

假定NSHT在15 km的高度由载机以Ma数1释放，经过助推、翻转后，超燃冲压发动机开始工作进入高速巡航段，其中有动力跳跃3次、无动力滑翔跳跃2次。最大飞行Ma数5.5，最大巡航高度50.85 km，最大加速度4.01g，最大的角速度0.024 rad/s，全程飞行1 024 s，航程1 557 km。

3.1 仿真场景1

从图1可以看出采用不同自适应采样准则的跟踪滤波轨迹RMS-IMM算法与CA以及Singer自适应采样算法都能实现目标跟踪。当目标运动较为稳定机动较弱时，自适应采样算法采样点稀疏；目标处于跳跃节点或者机动较强时，采样点较为密集。RMS-IMM算法基于机动强度自适应调整采样间隔使采样点分布更加合理，机动较弱的巡航滑翔段采样点间隔较大，在“蛇形”跳跃的峰值和谷值位置采样间隔较小。此外，由图2可知，RMS-IMM算法与CA，Singer自适应采样算法位置RMSE整体水平相当，CA与Singer自适应采样算法出现多个误差尖峰，RMS-IMM算法相对突变点较少，整体水平较为均衡。

图1 滤波轨迹与真实值比较Fig.1 Comparison between tracking result and real value

图2 σx=100 m，σy=100 m时滤波结果Fig.2 Comparison of tracking result when σx=100 m and σy=100 m

图3反映了3种自适应采样准则在不同时刻的采样率。可以看到RMS-IMM，CA，Singer自适应准则根据目标运动状态自适应调整采样率，机动较强的跳跃转弯时刻采样率上升，机动较弱时采样率较低。针对滤波初期采样间隔初值设置不合理的问题，CA，Singer自适应变采样算法收敛速度较慢，采样率出现多个冲击点。RMS-IMM基于指数形式的主导因子能快速收敛到较为合适的采样间隔，对指数参数的修正减小单次采样率调整偏差导致误差累积，避免在转弯机动时刻采样率尖峰点的问题。此外，RMS-IMM自适应采样准则引入平滑因子提高了采样率稳定性。总体上，RMS-IMM采样率随目标机动强度变化趋势明显，采样率曲线平滑，鲁棒性较好；CA自适应采样准则次之，在目标机动时采样率容易出现突变点；Singer自适应采样准则效果较差，采样间隔计算收敛速度较慢，受噪声随机影响较大，突变点数量较多。

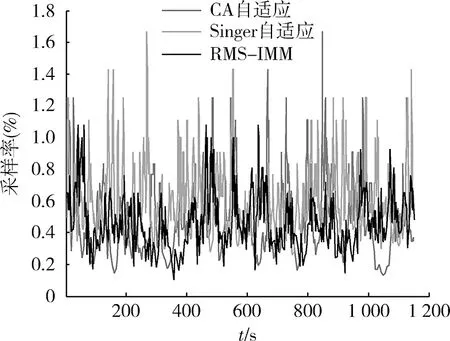
图3 σx=100 m，σy=100 m时采样率比较Fig.3 Comparison of sampling rate when σx=100 m and σy=100 m

3.2 仿真场景2

当观测噪声误差标准差分别为σx=σy=400 m时，RMS-IMM算法与传统算法采样率比较如图4所示。

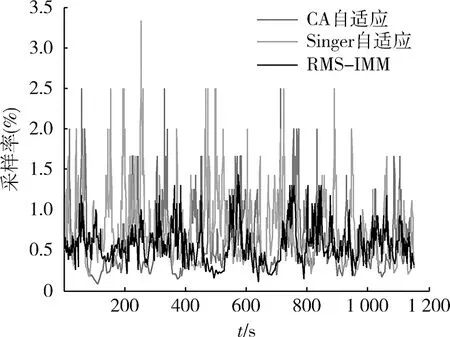
图4 σx=400 m，σy=400 m时采样率比较Fig.4 Comparison of sampling rate when σx=400 m and σy=400 m

系统噪声增大时，3种自适应采样算法总体采样率整体水平都随之提升， 基本实现了随目标机动的自适应采样率调整。CA，Singer自适应算法采样率起伏较大，突变点显著增多，鲁棒性较差，RMS-IMM算法自适应采样准则能更精确的反映目标机动变化，基于平滑因子控制，采样率曲线较为平滑，稳定性更高。本文仿真只添加较为简单的高斯白噪声，但在实际雷达探测临近空间高超声速目标时噪声环境更加复杂，RMS-IMM算法稳定性体现将更加显著。

3.3 算法总体性能评价

针对每一次Monte Carlo采样点数与采样时间不确定的问题，修改传统统计评价指标作为衡量算法的整体性能参数。

总体均方差(单位m)为

(17)

相对误差压缩比为

(18)

平均采样点数为

(19)

式中：M，Nt分别为Monte Carlo次数、第t次仿真采样点数；X(k|k)，X(k)，Z(k)分别为滤波值、真实值、量测值。

表1反映了3种算法的总体性能。可以看出当系统观测噪声标准差为100 m时，Singer，RMS-IMM算法x轴总体均方差在92 m左右波动，由于x轴有较长时间弱机动导致CA自适应x轴跟踪精度相对较低，但整体相差最大不超过10；y轴总体均方差值集中于90 m附近，相对误差压缩较为接近。当系统噪声增大时，自适应算法的位置总体均方误差和采样点数都随之增加。3种自适应变采样算法总体均方误差相当，相对误差压缩比之间相差较小。基于以上分析3种算法跟踪精度相近，RMS-IMM算法的观测点数最少。

表1 3种算法体性能比较Table 1 Comparison of performances of three algorithms

仿真结果说明了本文提出的RMS-IMM自适应变采样算法跟踪NSHT的可行性和有效性，相同的噪声环境下，图2表明该算法与传统自适应变采样算法位置整体误差均方根值较为接近。针对传统CA，Singer自适应采样准则适应性问题，RMS-IMM算法基于前后相邻时刻滤波位置残差设计主导因子，通过协方差偏差修正指数参数保持较为稳定的跟踪精度，避免采样间隔误差累积导致后续跟踪精度降低。考虑到CA，Singer自适应算法采样率出现多个突变点的问题，引入平滑因子，提高采样率稳定性。图3，4表明RMS-IMM算法较CA，Singer自适应变采样算法能更准确的表征目标机动，在系统噪声增大时CA，Singer自适应算法采样率突变点增多且峰值变大，经过平滑处理的RMS-IMM算法对采样率冲击点抑制效果显著，突变点较少，采样率更加稳定。当机动较弱时，在不严重牺牲跟踪精度的情况下RMS-IMM算法能快速适应目标当前运动，及时增大采样间隔，减少观测次数提高实时性；当机动较强时，RMS-IMM根据机动强度合理减小采样间隔(当精度到达某一程度时，减小采样间隔对精度提高效果并不理想)，能更好的平衡跟踪精度与采样点数的关系，其费效比更高。结合表1，RMS-IMM算法在采样点数较CA，Singer更少，具有更低的资源占用率。

4 结束语

本文提出的相对机动RMS-IMM自适应变采样算法有效克服了传统CA，Singer自适应变采样算法采样率针对单一模型、稳定性差的缺陷。跟踪精度相近的条件下，RMS-IMM算法采样率稳定性、机动适应性、采样点数都优于传统自适应变采样算法，是一种较为可行的NSHT跟踪算法，对NSHT跟踪策略与跟踪参数研究有一定的参考价值。如何进一步提高算法在目标机动时的适应性，是下一步将要进行的工作。

[1] 聂万胜,罗世彬,丰松江,等.近空间飞行器关键技术及其发展趋势分析[J].国防科技大学学报,2012,34(2):107-113. NIE Wan-sheng, LUO Shi-bin, FENG Song-jiang, et al. Analysis of Key Technologies and Development Trend of Near Space Vehicle[J].Journal of National University of Defense Technology, 2012,34(2):107-113.

[2] 秦雷,李君龙,周荻. 基于交互式多模型算法跟踪临近空间目标[J]. 系统工程与电子技术,2014,36(7):1243-1249. QIN Lei， LI Jun-long, ZHOU Di. Tracking for Near Space Target Based on IMM Algorithm[J]. Systems Eengineering and Electronics, 2014,36(7):1243-1249.

[3] GUAN Xin,ZHAO Jing. Resarch on Tracking Technology the Hypersonic Aircraft Based on IMM[C]∥ the 2011 International Conference on Wavelet Analysis and Pattern Recognition,2011:50-54.

[4] LAN Jian, LI Xiao-rong, MU C D. Best Model Augmentation for Variable-Structrue Multiplemodel Estimation[J].IEEE Trans. on Aerospase and Electronic Systems,2011,47(3):2008-2025.

[5] COHEN S A. Adaptive Variable Update Rate Algorithm for Tracking Targets with a Phased Array Radar[J].IEE Proc,of Radar Signal Process, 1986, 133(3): 277-230.

[6] VAN KEUK G, BLACKMAN S S. On Phased-Array Radar Tracking and Parameter Control[J]. IEEE Trans. on Aerosp Electron Syst, 1993,29(1):186-194.

[7] COETZEE S L, WOODBRIDGE K, BAKER C L. Multifunction Radar Resource Management Using Tracking Optimization [C]∥The IEEE the International Radar Conference, 2003:578-583.

[8] 鉴福升,徐跃民,阴泽杰.基于IMM的电扫描雷达参数控制算法研究[J]. 中国科学技术大学学报,2010,40(3):294-298. JIAN Fu-sheng, XU Yue-min, YIN Ze-jie. Research of Parameter Control Algorithm for Electronically Scanned Radar Based on IMM[J]. Journal of University of Science and Technology of China, 2010,40(3):294-298.

[9] 卢建斌,胡卫东,郁文贤. 基于协方差控制的相控阵雷达资源管理算法[J]. 电子学报,2007(3):402-408. LU Jian-bin, HU Wei-dong, YU Wen-xian. Resource Management Algorithm Based on Covariance Control for hased Array Radars[J]. Acta Electronica Sinica,2007(3):402-408.

[10] 郁卫华,朱翔,朱晓华. 基于交互式多模型粒子滤波的相控阵雷达自适应采样[J]. 电子设计工程,2012,20(5):29-32. YU Wei-hua, ZHU Xiang, ZHU Xiao-hua. Adaptive Sampling Method for Phased Array Radar Based on Interacting Multiple Model Particle Filter[J]. Electronic Design Engineering,2012,20(5):29-32.

[11] ZHANG Zhen-kai, ZHOU Jian-jiang, WANG Fei, et al. Multiple-Target Tracking with Adaptive Sampling Intervals for Phased-Array Radar[J]. Journal of Systems Engineering and Electronics ,2011,22(5):760-766.

[12] CHENG Ting, HE Ze-shu, TANG Ting. Dwell Scheduling Algorithm for Multifunction Phased Array Radars Based on the Scheduling Gain[J]. Journal of Systems Engineering and Electronics, 2008,19(3):479-485.

[13] Émilie Winter, Philippe Baptiste. On Scheduling a Multifunction Radar[J]. Aerospace Science and Technology, 2007(11):289-294.

[14] QU Hong-quan, PANG Li-ping, LI Shao-hong. A Novel Interacting Multiple Model Algorithm [J]. IEEE trans. on Signal Processing,2009(89):2171-2177.

[15] CHENG Ting, HE Ze-shu, TANG Ting. An IMM-Based Adaptive-Rate-Target Tracking Alogrithm for Phased-Array Radar[J]. International Symposium on Intelligent Signal Processing and Communication Systems,2007(28):854-857.

[16] LIU Wei-feng, CHAI Zhong, WEN Cheng-Lin. Multi-measurement Target Tracking by Using Random Sampling Approach[J]. Acta Automatica Sinica, 2013,39(2):164-174.

[17] CHENG Ting, HE Ze, TANG Ting. Adaptive Update Interval Tracking Based on Adaptive Grid Interacting Multiple Model[J]. IET Radar Sonar Navig,2008, 2(2):104-110.

[18] 张武,赵宗贵,赵丰,等. 常加速目标纯方位跟踪最优观测者轨迹及仿真分析[J].解放军理工大学学报：自然科学版，2009,10(SL):11-15. ZHANG Wu, ZHAO Zong-gui, ZHAO Feng, et al. Optimal Observer Trajectory and Simulation Analysis for Bearings-only Tracking of Constant Acceleration Target [J]. Journal of PLA University of Science and Technology：Natural Science ed,2009,10(sl):11-15.

[19] LI Wen-lin, JIA Ying-min. Location of Mobile Station With Maneuvers Using an IMM Based Cubature Kalman Filter[J]. IEEE Trans. on Industrial Electronics, 2012, 59(11):4388-4348.

[20] ZHANG Min, JIA Hai-tao,SHEN Zhen. Improved Resampling Procedure Based on Genetic Algorithm in Particle Filter[J]. Journal of University of Electronic Science and Technology of China, 2015,44(3):344-349.

Adaptive Sampling Tracking Algorithm for Near Space Hypersonic Target

LI Fan1, BI Hong-kui2, DUAN Min2,YU Chen-long1

(1. Air Force Early Warning Academy,Department of Graduate Management,Hubei Wuhan 430019,China;2. Air Force Early Warning Academy,Hubei Wuhan 430019, China)

An interacting multiple model(IMM) based on relative maneuvering strength (RMS) is presented to solve the problem that traditional tracking algorithm can only applies to single model.According to the algorithm, motorized sensitive dominant gene is built to improve the sensitivity of tracking maneuver targets by comparing difference between the desired covariance matrix and that of the actual covariance and the threshold. In order to ensure the stability of adaptive sampling rate, a smoothing gene is introduced to design a linear equation. The simulation experiments show that, the three algorithms have similar tracking precision but the new algorithm lessens sampling points and mutational points, which proves that the new algorithm has better stability in the track data rate and sampling rate.

near space;hypersonic target; adaptive sampling; relative maneuvering strength(RMS); interacting multiple model (IMM); tracking data rate

2016-01-04；

2016-03-11

李凡(1992-)，男，土家族，湖南凤凰人。硕士生，主要从事临近空间高超声速目标跟踪算法方面研究。

10.3969/j.issn.1009-086x.2016.06.018

V423.9;TN957.51;TP301.6

A

1009-086X(2016)-06-0102-07

通信地址：430019 湖北省武汉市黄浦大街288号

E-mail：1746338543@qq.com