反坦克导弹带落角约束滑模导引律研究*

杨锁昌，张宽桥，李宝晨，张凯

(军械工程学院 导弹工程系，河北 石家庄 050003)

导航、制导与控制

反坦克导弹带落角约束滑模导引律研究*

杨锁昌，张宽桥，李宝晨，张凯

(军械工程学院 导弹工程系，河北 石家庄 050003)

为增大反坦克导弹终端落角，提高战斗部的毁伤效能，基于终端滑模控制理论，及弹目相对运动模型，选取弹目相对速度偏角作为滑模面，同时引入落角约束项，结合快速幂次趋近律，推导出了一种带落角约束的滑模导引律。采用有限时间控制理论对导引律的稳定性和有限时间收敛特性进行了证明。最后基于弹道仿真，将该导引律与带落角约束的偏置比例导引律进行了对比仿真分析，结果表明该导引律能够满足制导精度和末端落角约束的要求，脱靶量更小，落角控制精度更高，鲁棒性更强。

导引律；落角约束；相对速度偏角；有限时间收敛；终端滑模控制；快速幂次趋近律

0 引言

反坦克导弹是用于打击坦克、步兵战车等装甲目标的利器，为了提高反坦克导弹的毁伤效能，在确保对目标的精确打击的情况下，要求弹头以一定的落角击中目标，因此，在反坦克导弹末制导律的设计中必须考虑落角约束的问题。

自Kim等人首次在导引律中考虑落角约束问题以来，一些学者基于不同的理论方法提出了许多带落角约束的导引律，主要包括最优导引律、滑模变结构导引律、改进的比例导引律以及其他类型的导引律[1]。基于最优控制理论推导出的最优导引律不受性能指标和终端约束条件的限制，在理想情况下制导性能最佳，但依赖于各种假设和简化，鲁棒性较差[2-3]。改进的比例制导律，包括变系数比例导引律和偏置比例导引律等，结构形式简单，对测距、测速信息等要求不高，易于工程实现，但对于导引信息准确度要求较高，抗干扰能力差[4-5]。

由于滑模变结构控制在滑动模态对系统参数摄动和外界干扰具有不变性，因此，被广泛用于导引律的设计中。文献[6]基于滑模控制理论和Lyapunov稳定性理论，提出了一种带落角约束的滑模变结构导引律，并对抖振现象进行削弱，但只对固定目标进行了仿真分析。

传统滑模控制方法选取线性滑模面，当系统状态到达滑模面后会渐进趋近于平衡点，但不能保证有限时间收敛。终端滑模控制方法能够实现系统状态的有限时间收敛，且相比传统滑模控制方法具有更好的收敛性能[7]。文献[8-11]采用终端滑模控制理论设计了带落角约束的滑模导引律，并实现了系统状态的有限时间收敛。上述文献所设计的滑模导引律均选取弹目视线角速率或者弹目相对运动距离与视线角速率的乘积作为滑模面，但在制导末段，随着弹目距离的减小视线角速率会急剧增大，进而会产生很大的控制指令。针对这个问题，文献[12-13]选取弹目相对速度偏角作为滑模面，对导引律进行设计，取得了良好的制导效果，但没有对落角约束问题进行研究。

本文基于终端滑模控制方法，选取包含弹目相对速度偏角和落角约束项的滑模面切换函数，结合快速幂次趋近律，设计了一种带落角约束的滑模导引律，将目标机动视为有界干扰，采用有限时间控制理论对导引律的有限时间收敛特性进行了证明，并利用饱和函数法削弱抖振。仿真结果表明所设计导引律在命中精度、落角约束、抖振抑制等方面具有良好的制导性能。

1 问题描述

反坦克导弹的落角约束问题是在纵向平面内分析的，因此，本文仅对俯仰通道进行分析。假设导弹和目标均视为在平面运动的质点，图1给出了导弹和目标的相对运动关系。

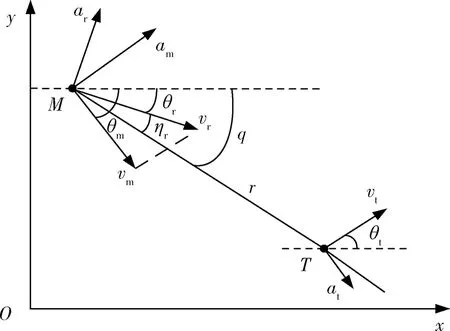
图1 纵向平面内弹目相对运动关系Fig.1 Missile-target motion model in longitudinal plane

在图1中，M表示导弹；T表示目标；vm为导弹的速度；θm为导弹的弹道倾角；am为导弹运动的法向加速度；vt为目标的速度；θt为目标的航迹倾角；at为目标运动的法向加速度；r为弹目之间相对距离；q为弹目视线角；vr为弹目相对运动速度，即vr=vm-vt；ar为弹目相对运动的法向加速度；ηr为弹目相对速度偏角，即弹目相对速度方向与弹目视线之间的夹角。规定所有角度逆时针方向为正，反之为负。

根据图1中弹目相对运动几何关系，可得弹目相对运动方程：

(1)

导弹的终端落角也称为攻击角，是制导末端导弹与目标速度矢量之间的夹角。对于具体的落角约束的制导问题，落角约束可以转化为视线角满足q(tf)=qd的问题[14]。在制导过程中，当弹目距离较小时，导引头会进入盲区，导弹按照惯性飞向目标。设导引头作用的最小距离为r0，则方程(2)中的时变参量r(t)应满足r(t) ≥r0。

2 预备知识

为便于下文对导引律有限时间收敛特性的分析和证明，首先对有限时间控制理论进行简要介绍。

考虑如下非线性系统:

(2)

式中：f:U0×R→Rn在U0×R上连续；U0是原点x=0的一个开邻域。

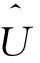
引理2[16]对于系统(2)，若存在连续、正定函数V(x)满足

(3)

式中：a,b>0；0<γ<1。

则系统状态到达稳定点的时间t取决于初值x(0)=x0，且满足不等式

(4)

3 带落角约束滑模导引律的设计

3.1 导引律的推导

为增强制导系统的鲁棒性，基于滑模控制理论对导引律进行设计，针对弹目视线角速率在制导末段变化剧烈的问题，同时考虑落角约束，选取如下终端滑模面

(5)

式中：k1>0；0<α<1；qd为期望落角。

由图1可以看出，q=θr+ηr，若ηr= 0，即q=θr，则弹目相对速度方向和弹目视线方向一致，导弹能够命中目标，且弹道较为平直。因此，滑模面第1项保证了导弹命中目标的要求，并且能够获得较为平直的弹道；滑模面第2项为落角约束项，能够保证落角约束的要求。

导弹的末制导时间是有限的，因此需要使制导系统状态在有限时间内快速趋近于滑模面。系统状态快速到达滑模面，导弹就能够及早的以较为平直的弹道飞行目标，能有效提高制导性能。基于上述考虑，选取快速幂次趋近律

(6)

式中：k3,k4>0；0<β<1。

由图1弹目相对运动关系可知

ar=amcos(q-ηr-θm)-atcos(q-ηr-θt)，

(7)

且

(8)

结合式(7)和式(8)可得

(9)

对式(5)进行微分得

(10)

将式(9)代入式(10)，然后结合式(6)可得

(11)

将式(11)整理后可得带落角约束的导引律

(12)

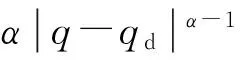
(13)

式(13)中存在分母项cos(q-ηr-θm)，对其非奇异性进行分析如下：

由图1可知

vr=vmcos(q-θm-ηr)-vtcos(q-θt-ηr),

(14)

变换后得

vmcos(q-θm-ηr)=vr+vtcos(q-θt-ηr)≥vr-vt.

(15)

弹目交战的过程中，导弹速度远大于目标速度，则弹目相对速度要大于目标速度，即vr-vt>0，而vm≠ 0，因此式(12)是非奇异的。

式(13)中还有未知量vr和ηr，其计算过程如下：

由弹目运动方程(1)的第1式和第2式，可得

(16)

对式(16)求解后得

(17)

3.2 稳定性和有限时间收敛特性分析

选取Lyapunov函数：

V=s2,

(18)

对式(18)求导后可得，并将导引律(13)代入得

(19)

由Lyapunov稳定性理论可知，系统是渐进稳定的。引理1可知，导引律(13)是有限时间收敛的，即在有限时间内系统状态能够收敛到滑模面s=0。式(19)可写为如下形式:

(20)

由引理2可得到系统收敛时间

(21)

导引律(13)中含有符号函数sgns，会产生抖振现象，采用高增益连续函数s/(|s| +δ)代替符号函数可有效削弱抖振，因此，导引律的形式可变为

(22)

式中：δ> 0，为一个较小的数，一般称为边界层厚度或消颤因子[17]。

为方便叙述，将所设计带落角约束的有限时间收敛终端滑模导引律(finite-time convergent terminal sliding mode guidance law,FCTSM)。

4 仿真分析

为验证本文所提导引律的有效性，将其引入某型反坦克导弹模型中，进行数字仿真分析。导弹的落角约束要求是通过纵向弹道方案实现的，横向弹道方案采用传统的比例导引律。在惯性坐标系下，选取导弹发射点为坐标原点，导弹初始位置为(0, 0, 0)m，目标沿Ox轴负方向机动，初始位置为(2 500, 0, 0)m，初始速度为10 m/s。导弹在Ox方向运动至1 000 m时进入末制导段，并设该时刻为仿真开始时间t=0 s。t>0 s时，目标开始做加速运动，加速度为5 m/s2，目标速度达到20 m/s时开始做匀速运动。设定落角约束为-60°。

为更好地分析本文导引律的制导性能，在仿真中还引入了文献[5]所提带落角约束的偏置比例导引律(bias proportional navigation guidance law, BPN)

(23)

仿真实验结果如表1和图2～5所示。

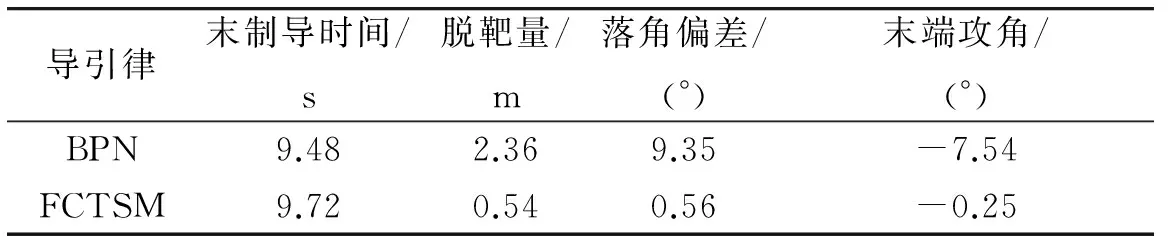
表1 2种导引律制导效果比较Table 1 Comparisons of guidance performance between two laws

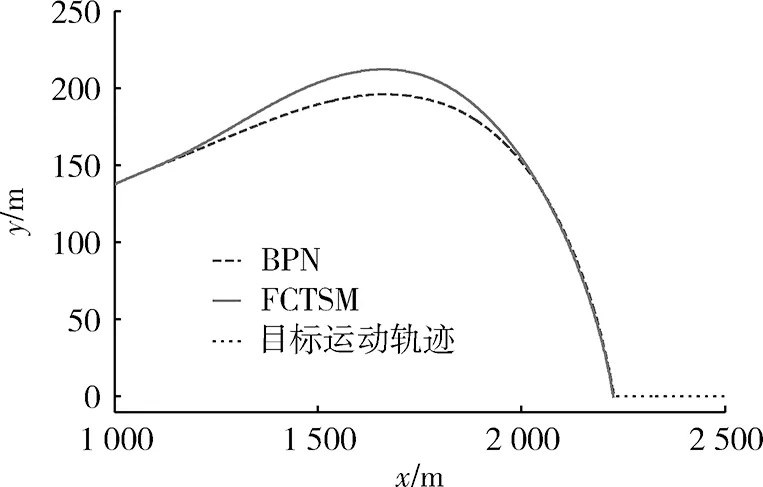
图2 弹目纵向相对运动轨迹Fig.2 Missile-target longitudinal trajectories

图3 导弹俯仰角曲线Fig.3 Pitching angle curves of missile

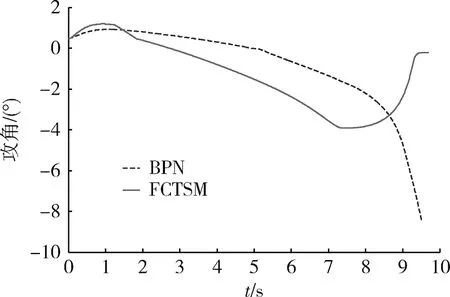
图4 导弹攻角曲线Fig.4 Attack angle curves of missile

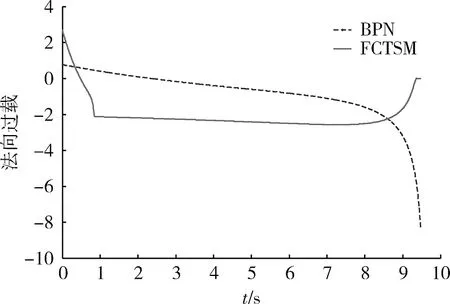
图5 纵向平面内导弹法向过载曲线Fig.5 Normal overload curves of missile in longitudinal plane

由表1可以看出，在2种导引律作用下，末制导时间差别不大，但FCTSM的脱靶量、落角偏差和末端攻角都明显小于BPN，并且BPN的脱靶量和落角偏差都较大。因此，可以说明在FCTSM作用下，导弹能够满足命中精度和落角约束的要求，并且FCTSM的制导性能要明显优于BPN。

由图2可以看出，FCTSM的弹道轨迹在制导初段较为弯曲，且弹道高度高于BPN，在制导末端弹道较为平直，这是由于FCTSM能够使导弹倾角较早的满足期望落角要求，实现俯仰角在制导段结束前收敛到期望落角。从图3可以看出，在FCTSM的作用下，导弹俯仰角能够有效时间内收敛到期望落角。从图4和图5可以看出BPN的攻角和过载在末端逐渐增大，这说明导弹在制导末端需要产生大的攻角(过载)用来调节弹道成形。分析原因主要是BPN随着剩余飞行时间的减少，期望落角没有达到期望值，导致导引律中落角约束项急剧增大，使得控制指令增大，使得导弹法向过载逐渐增加。而FCTSM的末端攻角逐渐收敛至零，这是由于FCTSM能够保证落角有限时间收敛到期望值，使导弹在末制导段结束前达到期望落角，并且由于滑模变结构的不变性，落角在末端基本保持不变，因此，导弹在末端弹道较为平直，大大减小了需用过载。从图4和图5中还可以看出，FCTSM对抖振进行了很好的抑制，没有出现抖振现象，并且针对机动目标表现出了良好的鲁棒性。

综上所述，对于打击机动目标，本文所设计的导引律FCTSM，能够使制导系统状态在有限时间内收敛到平衡点，系统没有抖振，并且其制导性能明显优于BPN，验证了所设计导引律的有效性和鲁棒性。

5 结束语

本文针对反坦克导弹终端落角约束问题，选取终端滑模面，包含相对速度偏角和落角约束项，设计了一种带落角约束的滑模导引律，对其有限时间收敛特性进行了分析和证明，并对抖振现象进行了削弱，引入导弹模型中进行对比仿真，检验了该导引律的有效性和优越性。所提导引律制导形式简单，易于工程实现，不仅可以运用于反坦克导弹，还能用于反舰导弹等制导武器，具有较广的适用范围。

[1] 蔡洪，胡正东，曹渊. 具有终端角度约束的导引律综述[J]. 宇航学报，2010, 31(2):345-323. CAI Hong, HU Zheng-dong, CAO Yuan. A Survey of Guidance Law with Terminal Impact Angle Constraints[J]. Journal of Astronautics, 2010, 31(2):345-323.

[2] RATNOO A, GHOSE D. State Dependent Riccati Equation Based Guidance Law for Impact Angle Constrained Trajectories[J]. Journal of Guidance, Control, and Dynamics，2009, 2(1): 20-326.

[3] TAUB I, SHIMA T. Intercept Angle Missile Guidance under Time Varying Acceleration Bounds[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(1): 83-96.

[4] RATNOO A, GHOSE D. Impact Angle Constrained Guidance Against Nonstationary Nonmaneuvering Targets[J]. Journal of Guidance, Control and Dynamics, 2010, 33(1): 269-275.

[5] 高峰，唐胜景，师娇，等. 一种基于落角约束的偏置比例制导律[J]. 北京理工大学学报，2014, 34(3):277-282. GAO Feng, TANG Sheng-jing, SHI Jiao, et al. A Bias Proportional Navigation Guidance Law Based on Terminal Impact Angle Constraint[J]. Transactions of Beijing Institute of Technology, 2014, 34(3): 277-282.

[6] 张亚松，任宏光，吴震，等. 带落角约束的滑模变结构制导律研究[J]. 电光与控制，2012, 19(1):66-68. ZHANG Ya-song, REN Hong-guang, WU Zhen, et al. On Sliding Mode Variable Structure Guidance Law with Terminal Angular Constraint[J]. Electronics Optics & Control, 2012,19(1):66-68.

[7] 穆朝絮，余星火，孙长银. 非奇异终端滑模控制系统相轨迹和暂态分析[J]. 自动化学报，2013, 39(6):902-908. MU Chao-xu, YU Xing-huo, SUN Chang-yin. Phase Trajectory and Transient Analysis for Nonsingular Terminal Sliding Mode Control Systems[J]. Acta Automatica Sinica, 2013, 39(6): 902-908.

[8] SACHIT R, DEBASISH G. Terminal Impact Angle Constrained Guidance Laws Using Variable Structure Systems Theory[J]. IEEE Transactions on Control Systems Technology, 2013(99):1-10.

[9] 周慧波，宋申民，刘海坤. 具有攻击角度约束的非奇异终端滑模导引律设计[J]. 中国惯性技术学报，2014, 22(5):606-611, 618. ZHOU Hui-bo, SONG Shen-min,LIU Hai-kun. Nongsingular Terminal Sliding Mode Guidance Law with Impact Angle Constraint[J]. Journal of Chinese Inertial Technology, 2014, 22(5):606-611,618.

[10] 熊少锋，王卫红，王森. 带攻击角度约束的非奇异快速终端滑模制导律[J]. 控制理论与应用，2014, 31(3): 269-278. XIONG Shao-feng, WANG Wei-hong, WANG Sen. Nonsingular Fast Terminal Sliding-Mode Guidance Law with Intercept Angle Constraint[J]. Control Theory & Applications, 2014, 31(4):269-278.

[11] KUMAR S R, RAO S, GHOSE D. Nonsingular Terminal Sliding Mode Guidance with Impact Angle Constraints[J]. Journal of Guidance, Control and Dynamics, 2014, 37(4): 1114-1130.

[12] 郭鸿武，林维松，刘明俊. 基于相对速度偏角的变结构导引律[J]. 宇航学报，2001, 22(3):33-37. GUO Hong-wu, LIN Wei-song, LIU Ming-jun. A Variable Structure Guidance Law Based on Relative Velocity Deflection Angle[J]. Journal of Astronautics, 2001, 22(3):33-37.

[13] 林嘉新，赵永涛，胡云安. 基于零化相对速度偏角的变结构末制导律设计[J]. 海军工程学院学报，2009, 24(6): 646-650. LIN Jia-xin, ZHAO Yong-tao, HU Yun-an. Design of a Variable Structure Terminal Guidance Law Based on Relative Velocity Deflection angle[J]. Journal of Naval University of Engneering, 2009, 24(6):646-650.

[14] 刁兆师，单家元. 带末端攻击角约束连续有限时间稳定制导律[J]. 宇航学报，2014, 35(10):1141-1149. DIAO Zhao-shi, SHAN Jia-yuan. Continuous Finite-Time Stabilization Guidance Law for Terminal Impact Angle Constrainted Flight Trajectory[J]. Journal of Astronautics, 2014, 35(10): 1141-1149.

[15] 洪奕光，程代展. 非线性系统的分析与控制[M]. 北京：科学出版社，2005. HONG Yi-guang,CHENG Dai-zhan.Nonlinear System Analysis and Control[M].Beijing:Science Press,2005.

[16] YU S H, YU X H, SHIRINZADEH B Y, et al. Continuous Finite-Time Control for Robotic Manipulators with Terminal Sliding Mode[J]. Automatica, 2005, 41(11): 1957-1964.

[17] 贾庆忠，刘永善，刘藻珍. 电视制导侵彻炸弹落角约束变结构反演制导律设计[J]. 宇航学报，2008, 29(1):208-214. JIA Qing-zhong, LIU Yong-shan, LIU Zao-zhen. Variable-Structure Back Stepping Guidance Law with Terminal Angular Constraint for Video Guided Penetrating Bomb[J]. Journal of Astronautics, 2008, 29(1): 208-214.

Sliding Mode Guidance Law with Impact AngleConstraint for Antitank Missile

YANG Suo-chang, ZHANG Kuan-qiao, LI Bao-chen, ZHANG Kai

(Ordnance Engineering College, Missile Engineering Department, Hebei Shijiazhuang 050003, China)

To increase the terminal impact angle to enhance the damage efficiency of the warhead, a sliding mode guidance law with impact angle constraint based on terminal sliding mode control theory and missile-to-target motion model is proposed. The guidance law selects relative velocity deflection angle and impact angle constraint as the sliding mode surface, and combines with the fast power reaching law. The stability and finite-time convergent feature of the guidance law is proved with the finite-time control theory. Finally, the law is compared with bias proportional navigation guidance law with impact angle constraint based on trajectory simulation. Simulation results show that the designed guidance law can meet the requirement of guidance precision and terminal impact angel constraint, and has less miss distance, higher impact angle control accuracy, and stronger robustness.

guidance law; impact angle constraint; relative velocity deflection; finite-time convergence; terminal sliding mode control; fast power reaching law

2015-09-10；

2016-04-30

杨锁昌(1969-)，男，河北定州人。教授，博士，主要研究方向为精确制导理论与技术。

10.3969/j.issn.1009-086x.2016.06.007

TJ761.1+2;TJ765

A

1009-086X(2016)-06-0037-06

通信地址：050003 河北省石家庄市和平西路97号导弹工程系

E-mail：yangsuochang_jx@sina.com