弹炮结合防空系统作战部署建模与分析*

刘鸿福，翁郁，王志强

(国防科技大学 机电工程与自动化学院，湖南 长沙 410073 )

空天防御体系与武器

弹炮结合防空系统作战部署建模与分析*

刘鸿福，翁郁，王志强

(国防科技大学 机电工程与自动化学院，湖南 长沙 410073 )

对弹炮结合防空系统部署的依据和方法进行研究，在线形、扇形和环形3种基本的部署模型基础上，详细分析了弹炮结合防空系统的杀伤区范围及主要参数，并在此基础上解算了杀伤区的特征值计算模型，利用任务规划系统进行软件仿真，验证了模型的正确性。

任务规划；弹炮结合防空系统；火力防区；兵力部署；火力分配原则；防御体系建模

0 引言

目前在低空、超低空防御体系中主要存在3种防空武器，一是防空导弹；二是自行高炮；三是弹炮结合防空武器系统。弹炮结合防空武器系统作为野战和要地防空的重要武器装备，同时也是末端防御的重要手段。

弹炮结合防空系统是近年来新兴的防空武器系统，但发展和应用很快。现今各国都研制了不少弹炮结合武器系统。目前国外主要在以下2个方面大幅运用弹炮结合防空系统。一是作为末端防御的重要手段对巡航导弹的末端攻击进行快速有效防御；二是作为高机动和高密集火力的重要防御手段伴随装甲部队，对武装直升机等高机动目标实施实时精确快速防御。

本文主要是针对弹炮结合防空系统防空进行分析研究，通过构建模型、研究战术战法，提出合理有效的作战任务规划方法。其研究有助于提升弹炮结合防空系统的作战使用效能，有助于更加深入理解联合作战中各兵种的协同配合，为今后的作战运用提供理论依据。

1 弹炮结合防空系统的杀伤区建模

1.1 火力防区划分与建模

高炮射程较近、反应较快，一般都是针对近前目标进行作战[1]，它的防空区主要由有效射程、有效射高、射程死角和最大射角4个因素确定[2]。防空导弹火力准备时间较长，单发毁伤概率高，一般都是针对中远程目标进行作战，它的防空区域主要由射程远界、射程近界、作战高界和低界确定[3]；同时，防空导弹还可以对过航目标进行攻击，本文只分析过航前后射程远界相同的情况。

根据不同距离下导弹和高炮的毁伤概率特点来看[4]，对于导弹而言，不同的杀伤近界对整体的毁伤效能影响不大，本文只讨论杀伤近界为1 km的导弹；在杀伤近界之前存在作战死区，从杀伤近界到正常工作区需要500～1 000 m的缓冲距离，这一段距离虽然有防空作战的能力，但作战效能不稳定，不作为导弹的火力防区。对于高炮而言，在最大有效射程附近的毁伤概率较低，对目标威胁性较小，所以此区域不作为高炮的火力防区。

在火力防区划分时，需要给高炮留足完成一个长度为2 s的点射时间，也就是大概1.5 km。考虑到高炮为多发点射射击，一个点射的总毁伤概率较大，所以可以将其火力防区适当扩大。为了保证更加明确地区分高炮和导弹的火力防区，避免火力分配混乱，火力重叠区不宜太大。

根据上述分析，确定以下建模原则：

(1) 高炮攻击区从0距离开始，防区远界的毁伤概率不能低于0.4；

(2) 导弹攻击区的起始端要至少大于发射近界500 m；

(3) 导弹攻击区的平均毁伤概率不能低于0.65；

(4) 火力重叠区范围不宜超过1 km。

建立以下火力防区模型，并计算相关的平均毁伤概率：当斜距离小于1.5 km时，火力防区为高炮攻击区，平均毁伤概率为0.62；当斜距离1.5～2 km时，火力防区为火力重叠区，平均毁伤概率为0.7；当斜距离大于2 km时，火力防区为导弹攻击区，平均毁伤概率为0.68。

1.2 火力分配原则与建模

火力防区划分完成之后，需要对各防区的火力进行分配，以达到最好的防御效果。对于弹炮结合防空系统而言，当目标处于高炮攻击区内时，必须由高炮进行火力攻击；当目标处于导弹攻击区内时，必须由导弹实施火力打击；当目标处于火力重叠区时，高炮和导弹皆能攻击，为避免火力分配混乱，需要建立分配原则，并进行简单建模[5]。

火力重叠区的火力分配需要解决的核心问题是在该区域内的目标用哪种武器打击更有效。这要从2个方面考虑：一是弹炮结合防空系统本身作战性能。导弹和高炮的单独作战方式有很大差别。导弹发射基本上不需要提前量，只要导弹瞄准锁定目标就可以发射；而高炮射击必须要在火控系统给出提前量、随动系统调转火力到目标未来点的情况下才能击发[6]。另外，导弹的飞行速度快，具有自导跟踪的能力，对于机动灵活的目标可以实施跟踪打击，并且单发毁伤概率较高[7]；而高炮初速慢，主要是依靠数量优势产生的面杀伤达到拦截效果，炮弹自身没有机动性，弹道比较单一，比较适合拦截航迹固定的飞行目标。二是来袭目标的特点。目标的飞行速度、机动过载能力、目标价值将很大程度上决定拦截方式的变化。

根据上述分析，确定以下火力分配原则：

(1) 高速度目标由导弹拦截；

(2) 低机动能力目标由高炮拦截；

(3) 低价值目标由高炮拦截。

在上述分配原则的基础上以目标速度v、机动过载能力g和目标价值w为基本参数建模。目标权函数表示为

T=vα1+gα2+wα3,

(1)

式中：α1，α2和α3为权重系数，表示各参数的重要程度。

用层次分析法[8]对权重系数进行评估，通过两两比较，确定权重大小。假设专家评估结果为：机动过载能力相对于目标速度要重要，分数值为6∶5；目标速度相对目标价值要重要，分数值为7∶6。则通过计算可以得出α1=0.33，α2=0.39，α3=0.28。各参数的具体数值通过分段取值法可以进行量化，将量化值代入目标函数就可以求出目标函数值。目标函数值越大，越适合导弹拦截，目标函数值越小，越适合高炮拦截。

2 兵力部署模型的构建与效能分析

2.1 兵力部署模型

根据防空系统作战的基本规律、基本原则，弹炮结合防空系统的兵力部署依据主要有以下4个方面：

一是保护目标的情况；二是敌方使用的兵力；兵器及采用的战术技术手段；三是我方兵力的数量及装备的作战性能；四是保卫同一目标的友邻部队部署情况。

根据不同的实际情况，弹炮结合防空系统的部署模型是多种多样的，但就基本模型而言，主要有线形部署、扇形部署和环形部署3种模型[9]。

线形部署是在敌方可能的主要来袭方向上，将防空兵力沿保卫区域呈一线配置。该部署方式能够形成较大的拦截正面宽度，但火力纵深小，防线容易被破坏，一旦某一防御点被突破，剩余的防御力量将很难收缩支援。此防御方式适用于防御范围较大的矩形防御区域，也适合背靠强大的后方保护或者天然地形屏障，以及敌方多航路、宽正面来袭等情况。

扇形部署是在我方兵力不够充足的情况下使用，在防御区域的主要作战方向上，将防御兵力以扇状的方式配置。其突出优点是节约兵力，通过集中兵力，在主要作战方向形成严密的火力防御网，抗击能力强。但是这种部署方式的可靠性较差，如果敌方改变进攻方向，便会避开火力防区，造成重大失误，风险较大。因此，扇形部署可以和环形部署搭配使用，外圈防御区在可能的主要作战方向采用扇形部署，内圈防御区采用环形部署。

环形部署是在己方兵力比较充足，并且敌进攻方向不明确时使用，在保卫目标周围以环形的方式部署兵力。环形部署具有很强的防御能力，能顾及到所有可能的作战方向，具有全方位的抗击能力，可靠性高。对于特别重要的目标，还可以采取多层环形部署，增大防御纵深，进一步提高防御的可靠性。但是其不足也很明显，对于同一个保卫目标，其需要的兵力数量最多。

对于上述建立的3个部署模型，可以从2方面进行优化：一是在一定数量的火力单元的情况下，通过调整各火力单元之间的相对位置关系，尽可能地增大防御角和防御宽度；二是在满足一定防御角和防御宽度的防御要求下，通过理论分析比较，选择最优的部署模型，使得所需火力单元最少。

2.2 模型理论分析

在地面防空过程中，有两种常规的防空方式，一是将投弹目标拦截在可投弹的最远范围之外，这一防空区域叫做投弹区[10]；二是将来袭的空中目标拦截在最大杀伤范围之外，这一防空区域叫做安全区。本文以下涉及到的理论分析均是针对投弹区展开研究，安全区的防御模型分析可以类比于投弹区。

对于具有远距离投弹的空中目标，尽可能多的将其拦截在投弹区之外能够最大限度地减少空中目标的数量，大幅增强防空效能，减少空袭损失。

投弹区的计算公式如下：

RT=rm+rs+rt，

(2)

式中：RT为投弹区的半径；rm为保卫目标的半径；rs为空袭武器的毁伤半径；rt为投弹目标水平投弹距离。

对于自杀式无人机、巡航导弹和弹道导弹等类似的不需要投弹的空袭兵器，其不具有投弹区，只能在安全区之外拦截[11]，因此，安全区的确定也至关重要。

安全区的计算公式如下：

RA=rm+rs，

(3)

式中：RA为安全区的半径。

掩护角是指防御兵力能够对保卫目标提供的防御角度，掩护宽度是指防御兵力能够在正面对保卫目标形成横向防御线的长度。这2个防御要素是评价防御系统优劣的重要指标，其中掩护角尤为重要。

在部署弹炮结合防空系统时，为了以最合理的方式、最少的兵力完成部署，需要对每一个火力单元的掩护角和掩护宽度进行计算，尽量减少火力重叠区[12]。图1表示了火力单元对投弹目标的各拦截要素之间的关系。

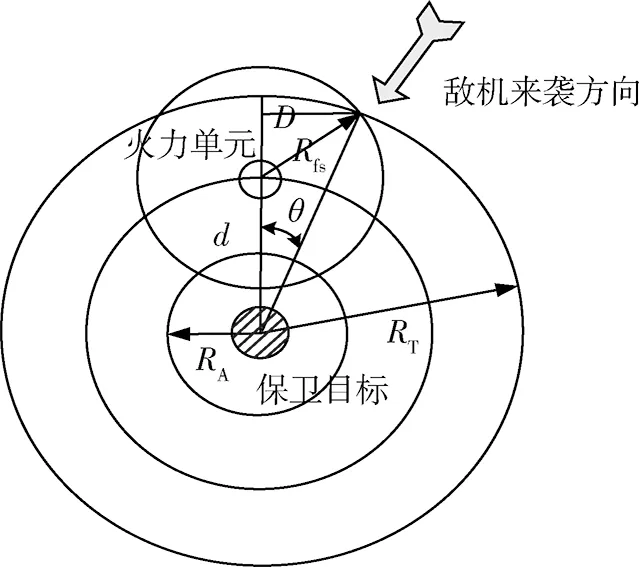
图1 火力单位拦截要素示意图Fig.1 Fire units to intercept features

图1中，Rfs表示火力单元的杀伤远界，d表示为火力单元部署点距保卫目标中心的距离，2θ表示为掩护角，2D表示为掩护宽度[13]。由图中关系可知，计算掩护角和掩护宽度之前需要对d，RT，Rfs之间的大小关系进行比较。

当d≤Rfs-RT时，

2θ=360°; 2D=+∞.

(4)

2D=+∞表示投弹目标无法在保卫目标正面实施有效投弹。

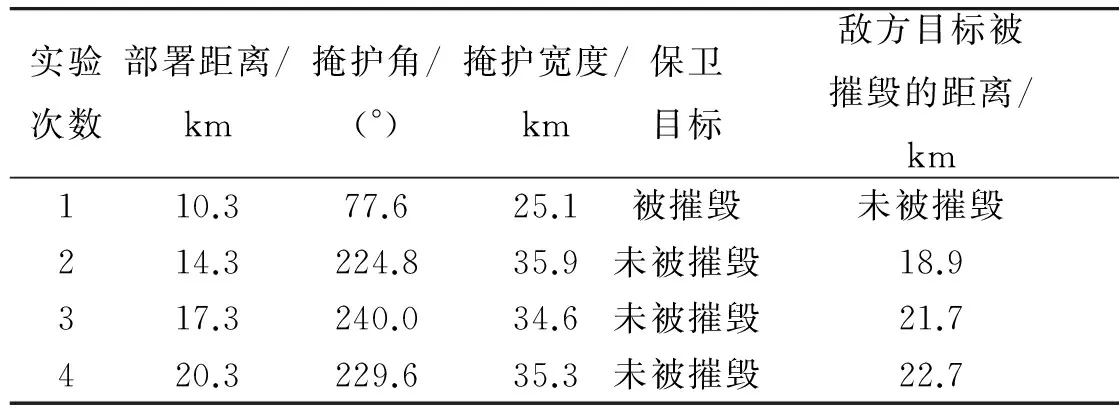
当Rfs-RT

(5)

当d≥Rfs+RT时，

(6)

当弹炮结合防空系统以线形方式部署时，可计算其掩护宽度和掩护角[14]：

Lx=N2D;αx=arctanNtanθ,

(7)

式中:Lx为线形模型的掩护宽度;αx为线形模型的掩护角;N为火力单元的个数。

当弹炮结合防空系统以扇形方式部署时，可计算其掩护宽度和掩护角：

(8)

式中：αs为扇形模型的掩护角；Ls为扇形模型的掩护宽度。

当弹炮结合防空系统以环形方式部署时，可计算其掩护宽度和掩护角：

Lh=+∞;αh=360°，

(10)

式中：Lh为环形模型的掩护宽度；αh为环形模型的掩护角。

对于不同的兵力部署模型，其防御要求的不同会影响所需火力单元的总数。

线形部署以防御宽度作为防御要求，若所需防御宽度为L，则所需火力单元总数：

(11)

式中：[ ]为取整符号。

扇形部署以防御角作为防御要求，若所需防御角为α，则所需火力单元总数：

(12)

环形部署以防御区域半径作为防御要求，若所需防御半径为R(R≥RT)，将式(4),(5)中的RT用R代替，则可以得到所需火力单元总数：

(13)

弹炮结合防空系统火力单元的相对位置因部署方式的不同而有所区别。

如果采用线形部署的方式，其火力单元之间的部署距离dx为

dx=2D，

(14)

式中：2D为火力单元掩护宽度，具体计算见式(5)和式(6)。

如果采用扇形部署的方式，当被掩护目标为大面积掩护对象时，火力单元与被掩护对象的距离则较大，式(14)仍基本适用。由于环形部署与扇形部署类似，所以，其火力单元之间的相对位置仍然可以采用式(14)。

3 实验与分析

利用任务规划软件[15]，对于第2节中建立的模型通过实验仿真进行验证。

根据第2节掩护角和掩护宽度计算模型可以分别计算出达到最大防御角和防御宽度时部署点距离保卫目标中心的距离。当以线形方式部署时，最优部署距离为17.3 km，掩护角为81.8°，掩护宽度为76.7 km，火力单元之间的间隔为19.2 km；当以扇形部署时，最优部署距离为17.3 km，掩护宽度为34.6 km，火力单元之间的间隔为17.3 km；当以环形部署时，最优距离为17.3 km，火力单元之间的间隔为17.3 km。

在仿真软件中将兵力按照上述计算结果进行部署，图2、图3和图4分别为线性部署、扇形部署和环形部署的仿真结果，从图中可以看出，优化部署的3种模型将所有的空中目标全部击落，达到了良好的防御效果。

图2 线性部署Fig.2 Linear deployment

图3 扇性部署Fig.3 Fan deployment

图4 环性部署Fig.4 Ring deployment

为了使实验结果更加可靠，基于上述作战任务想定，对扇形模型做了多次对比实验，将对比实验的结果进行统计比较。统计比较结果如表1所示。

表1 对比实验统计表Table 1 Comparative experimental statistics

当部署距离过近时，由式(5)和式(9)可计算得到的掩护角αs和掩护宽度Ls很小，火力单元在最远投弹区域附近的火力密度不够，以致敌机可以轻易躲避攻击，并且有机会发射空地导弹摧毁目标，没有达到防御的要求。

当部署距离较近时，部署的弹炮结合防空系统能够保卫好目标，尽管其可提供的掩护宽度Ls相对最优方案有一点点优势，但其可提供的掩护角αs和毁伤敌方目标的距离相对最优方案差距很明显。

当部署距离大于最优距离时，也能够保卫好目标，其可提供的掩护宽度Ls和毁伤敌方目标的距离已达到极限，并不随部署距离的大幅增加而有明显提高，基本上不影响防御体系的防御效果。而且其最重要的防御指标掩护角αs却有较明显的减小，对整个防御体系影响较大。相当于大幅度牺牲重要指标来小幅度提高次要指标，这不符合实际防御效能要求。

综上分析可知，此模型得出的最优距离是合理且正确的。

4 结束语

本文先是以单个弹炮结合防空系统为基础研究导弹和高炮的防区划分与火力分配问题，构建了防区划分模型，提出了火力分配原则。然后基于线形、扇形和环形3种最基本的防空部署模型，从掩护角、掩护宽度、兵力需求和火力单元之间的相对位置四个方面对3个部署模型构建了详细的计算模型，并通过仿真实验验证了计算模型的正确性，可以为弹炮结合防空系统的兵力部署提供有效的决策依据。

尽管论文对3个部署模型进行了详细的分析研究，但是由于武器装备本身的火力射击与毁伤能力难以量化，影响战场态势变化的因素较多，并且往往具有不可预测性，这使得论文中构建的理论计算模型与理论分析存在一定的不足，有待进一步研究与优化。

本课题涉及到的弹炮结合防空系统是一种比较新型的防空作战武器，其作战能力不能忽视，在实验中发现，弹炮结合战车中的防空导弹的速度、毁伤概率和装填时间对整个系统的毁伤能力有很大影响。因此弹炮结合防空系统中使用的近程防空导弹可比以往超高速方向发展，缩短反应时间，提高单发导弹的命中概率。

[1] 石磊.弹炮结合武器系统作战效能评估方法[D].北京：中国航天科工集团第二研究院，2006. SHI Lei.Research on Evaluation Method of Combat Effectiveness of Missile-Gun Combal Weapon System[D].Beijing:The Second Research Academy of CASIC,2006.

[2] 王凤山，李孝军，马栓柱.现代防空学[M].北京：航空工业出版社,2008. WANG Feng-shan, LI Xiao-jun, MA Shuan-zhu. Modern Air Defense Technology[M].Beijing: Aviation Industry Press,2008.

[3] 王克强.防空概论[M].北京：国防工业出版社,2012. WANG Ke-qiang. Antiaircraft Introduction[M]. Beijing: National Defense Industry Press, 2012.

[4] 马春茂，陈熙，侯凯，等.弹炮结合防空武器系统总体设计[M].北京：国防工业出版社,2008. MA Chun-mao, CHEN Xi, HOU Kai,et al. Missile-Gun Integrated Air Defense Weapon System Design[M]. Beijing: National Defense Industry Press,2008.

[5] LI D F. Fuzzy Multi Objective Many-Person Decision Makings and Games[M].Beijing National Defense Industry Press,2003,1：138-158.

[6] Grey Hawk. Cooperative Engagement Capability(CEC)[C]∥U.S.Washington D.C.: Network-Centric Air Defense, 2001,6.

[7] CHIANG J T.Defense Conversion and Systems Architecture: Challenges to Taiwan’s Aircraft Industry [J]. Technology in Society, 1999,21(3):263-274.

[8] 冯璐，高晓光. 层次分析法在多目标攻击逻辑与决策中的应用[J].西北工业大学学报,1998，17(4)：515-519. FENG Lu, GAO Xiao-guang. Application of Analytic Hierarchy Process in Multi-Objective Attack Logic and Decision Making.[J]. Journal of Northwestem Polytechnical University, 1998, 17(4): 515-519.

[9] 吴家明.地面防空武器系统混合部署方法研究[D].长沙: 国防科学技术大学，2009. WU Jia-ming. Study on Derivative-Free Algorithms in the Air-to-Sea Single Observer Passive Tracking Application [D]. Changsha: National University of Defence Technology, 2009.

[10] 王君，陆小平，娄寿春.防空作战运筹中的敌情、我情分析模型[J].现代防御技术,2002，30(3)：1-5. WANG Jun, LU Xiao-ping, LOU Shou-chun. The Situation Analysis Model in Air Defense Operation[J]. Modern Defense Technology, 2002, 30(3):1-5.

[11] 刘鸿福，潘梓逸，陶云.防空反导作战部署的评估问题初探[C]∥防空反导作战体系装备与技术发展论文集,北京：兵器工业出版社,2014. LIU Hong-fu, PAN Zi-yi, TAO Yun. Preliminary Assessment of Air Defense Missile Combat Deployment[C]∥Beijing: Ordnance Industry Press, 2014.

[12] YOU D D,WANG F,YANG H,et al.The Problem Research about Firepower Compatibity of the Surface Warship Air Defense[J].Fir Control & Command Control,2004,29(6):1603-1605.

[13] NAVEH B Z，GUI A，LEVY E，et al. Theater Ballistic Missile Defense[C]∥ AIAA,2008,9:89-106.

[14] Boaz I Kaminer,Joseph Z Ben-Asher.A Methodology for Estimating and Optimizing Effectiveness of Non-Independent Layered Deifense[M].Wiley Inter Science 2009,8:119-129.

[15] 陈璟，任敏，刘鸿福,等.飞行器任务规划[M] .长沙：国防科大出版社，2014. CHEN Jing, REN Min, LIU Hong-fu,et al. Aircraft Mission Planning.[M]. Changsha: National University of Defence Technology, 2014.

Combat Deployment Modeling and Analysis of Air Defense System in Combination with Missile-Gun

LIU Hong-fu, WENG Yu, WANG Zhi-qiang

(National University of Defense Technology,College of Mechatronics Engineering and Automation,Hunan Changsha 410073, China )

Deployment rules and methods of air defense system in combination with missile-gun are studied. On the basis of three basic deployment models (linear, fan-shaped and circular), analysis is made in detail on kill area and main parameters of air defense system with a combination of missile-gun, and on this basis characteristic value computation model of kill area is computed, mission planning system is used to do simulation, and correctness of model is validated.

mission planning； missile-gun combination air defense system； fire defense area； force deployment;fire distribution principle; defense system model

2015-10-13；

2016-03-02

国家自然科学基金(61403411)

刘鸿福(1983-)，男，湖南衡阳人。讲师，博士，主要从事任务规划、智能系统、自主协同控制、轨迹优化领域的研究。

10.3969/j.issn.1009-086x.2016.06.002

E844；N945.12

A

1009-086X(2016)-06-0007-06

通信地址：410073 湖南省长沙市国防科技大学三院自动化所三室

E-mail：330767967@qq.com