卫星制导炸弹滑翔增程弹道分析*
2016-02-24张会勇薛震刘泽乾
张会勇,薛震,刘泽乾
(空军航空大学,吉林 长春 130022)
导航、制导与控制
卫星制导炸弹滑翔增程弹道分析*
张会勇,薛震,刘泽乾
(空军航空大学,吉林 长春 130022)
针对卫星制导炸弹无动力的飞行特点,为实现滑翔增程目的,建立了滑翔增程弹道模型,采用使弹道上每点升阻比最大的思想进行弹道设计,该方法通过控制俯仰舵偏角来调节攻角的大小,使弹体产生向上的升力从而实现增程。对方案弹道进行了仿真分析,仿真结果表明:采用最大升阻比法的滑翔弹道下降趋势缓慢,增程效果显著。
制导炸弹;滑翔增程;弹道;升阻比;舵偏角;攻角
0 引言
卫星制导炸弹是现代高技术战争中重要的作战武器,在俄罗斯打击IS的空袭行动中,俄空军大量使用卫星制导炸弹取得了重大成功。为保护载机安全,卫星制导炸弹通常需要在敌防区外发射[1],这就要求制导炸弹具有滑翔增程的能力。制导炸弹的滑翔增程是指机弹分离后,通过弹上的制导控制系统控制俯仰舵偏转,使全弹产生一个攻角,由此增大作用在制导炸弹上的升力,使弹道下降趋缓,制导炸弹向前滑翔飞行实现增程的目的。
滑翔增程是目前采用的较为有效的一种弹箭增程技术[2-3],文献[4]利用庞特里亚金极小值原理对滑翔弹道最优控制参数进行了设计,文献[5]将极限值原理与粒子算法相结合,提出一种航空时敏炸弹增程弹道组合优化设计方法,文献[6]根据法向过载为0的思想,提出了一种近似平飞段的方案弹道,文献[7]利用连续微分动态规划法研究并求解弹箭的最优滑翔弹道,考虑到航空炸弹无动力特性,本文根据使炸弹飞行过程中每一时刻升阻比最大的原则进行滑翔增程段弹道设计,该方法计算量小,更适合弹载计算机实时快速解算的需求。
1 滑翔增程弹道模型
1.1 卫星制导炸弹作战过程
卫星制导炸弹作战过程可分为初始段、滑翔增程段和俯冲段。发射瞬间,由于炸弹处于载机下方不稳定气流当中,因此在发射后2 s的初始段不对炸弹进行控制[8];进入滑翔增程段后,通过控制俯仰舵机使全弹产生向上的升力,提高滞空时间实现增程效果;下降至一定高度后炸弹控制进入俯冲段,为保证制导炸弹精确高效的打击效果,通过带落角约束的末制导率控制炸弹以较大落角和速度的飞行弹道打击目标[9-10]。制导炸弹作战全过程如图1所示。

图1 卫星制导炸弹作战过程示意图Fig.1 Operation process of satellite guided bomb
1.2 增程段弹道模型建立
滑翔增程的原理是在制导炸弹飞行过程中通过控制俯仰舵产生一个比较确定的向上升力与重力平衡[11-12],使炸弹法向方向加速度很小,在空中停留时间较长从而飞行较远的距离,实现增程的效果。
为研究问题本质,本文只考虑炸弹在俯仰平面的运动,假设制导系统的作用是理想的,大气为标准气象条件,不考虑风扰动的影响,认为制导炸弹在滑翔飞行过程中只受空气动力和重力的影响,忽略其他次要力的作用[13]。基于以上基本假设,炸弹在滑翔段纵向质心运动模型可用如下方程表述:
(1)
(2)
X=qSCx0(α)(1+k1α2)+qSCx0(δ)(1+k2δ2),
(3)
(4)
(5)
(6)
(7)
δ(t)-δ*(t)=0,
(8)
式中:q=1/2ρv2,ρ为标准空气密度;v为炸弹飞行速度;S为弹体特征面积;m为弹重;X,Y为全弹阻力和升力;θ,α,δ,φ分别为炸弹滑翔段的弹道倾角、平衡攻角、俯仰舵偏角和摆动角速度;δ(t)为俯仰舵实际舵偏角规律;δ*(t)为俯仰舵设计的舵偏角规律,两者差值越接近0表示增程效果越理想。其他参数释义请参看文献[8]。
2 增程段弹道设计
在一定气动布局条件下,根据制导炸弹的飞行过程和基本原理,可通过控制俯仰舵偏角改变攻角大小,影响弹丸的运动轨迹[14-15],舵偏角过大致使攻角过大,会引发飞行稳定性问题,此外也会增加阻力,不利于滑翔增程;舵偏角过小,攻角也较小,滑翔增程效率降低。因此,在保证飞行稳定的前提下,得到合适的俯仰舵偏角与平衡攻角间的关系并进行控制,使增程段的滑翔效率提高。本文采用使滑翔弹道上每一点升阻比K最大的设计思想进行滑翔弹道的设计。
(9)
由式(7)可知Mz,α+Mz,δ=0时,理想弹道在滑翔飞行期间的任一瞬时都处于平衡状态,即舵面偏转时,作用在制导炸弹上的力矩在每一瞬时都处于平衡状态,则
(10)
由式(10)得单位舵偏角所引起的攻角为
(11)
式中:lα为翼体组合体压心到全弹重心的距离;lδ为俯仰舵压心到全弹重心的距离。
(12)
从式(12)中可知,升阻比不仅与炸弹的气动参数有关,还与其滑翔过程中的滑翔攻角和俯仰舵偏角有关。炸弹的设计变量一经确定,根据确定的气动力计算方法就可求得各气动参数。那么,为了求得升阻比,还需知道滑翔攻角和俯仰舵偏角的关系。
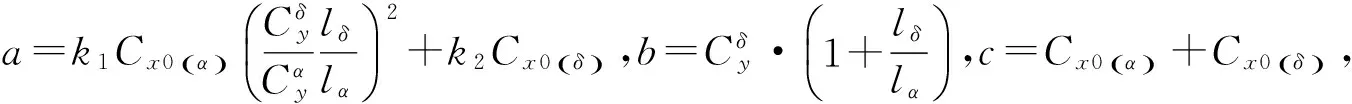

(13)
把式(13)代入力矩平衡关系式(10)中得到设计的平衡攻角

(14)
式(13)和式(14)就是根据升阻比最大所设计的滑翔增程段俯仰舵偏角和平衡攻角的变化规律。
3 弹道特性分析
使用四阶龙格—库塔法编写仿真程序,对某型卫星制导炸弹进行弹道特性仿真分析。弹体为轴对称布局,舵面和尾翼采用“+—+”形式配置。初始发射条件如下:发射高度y0=1.8 km,初始速度v0=290 m/s(Ma数0.85),初始弹道倾角θ0=-5°,弹重m=250 kg。高度降至0.3 km时炸弹结束滑翔增程进入俯冲段。仿真结果如图2~5所示。
从图2可以看出,攻角和舵偏角在滑翔初始一段时间内会产生震荡,最终攻角稳定在14.5°,舵偏角稳定在29°,α/δ=0.5。由于舵偏角从初始的0°突变到29°,舵片的活动就会使攻角产生过冲,短时间内攻角和舵偏角将会产生震荡直至稳定。平衡攻角是根据时刻俯仰舵提供的力矩和翼体组合体的稳定力矩达到平衡计算得出。
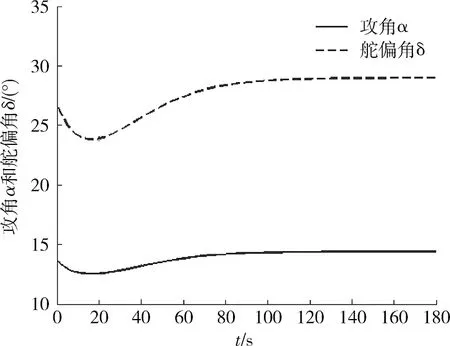
图2 俯仰舵偏角和攻角曲线Fig.2 Curves of rudder angle and attack angle
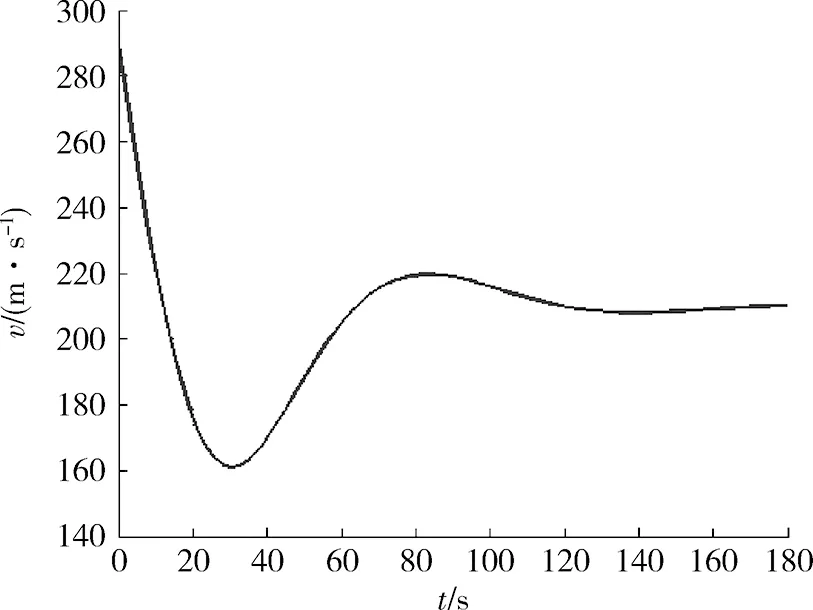
图3 滑翔增程段速度曲线Fig.3 Flight velocity of gliding extended range
图3中,由于炸弹无动力的特性,发射后在阻力作用下速度越来越小,升力与速度成正比例,所以也随之减小,弹体在重力作用下速度再次增大,最终稳定在210 m/s(Ma数0.6),此时弹体所受外力达到相对平衡,弹道上每一点升阻比都达到最大。

图4 增程段升阻比曲线Fig.4 Curve of lift-drag ratio of extended range
图4显示:在一定气动布局条件下,滑翔增程效果最佳的升阻比是K=2.96。
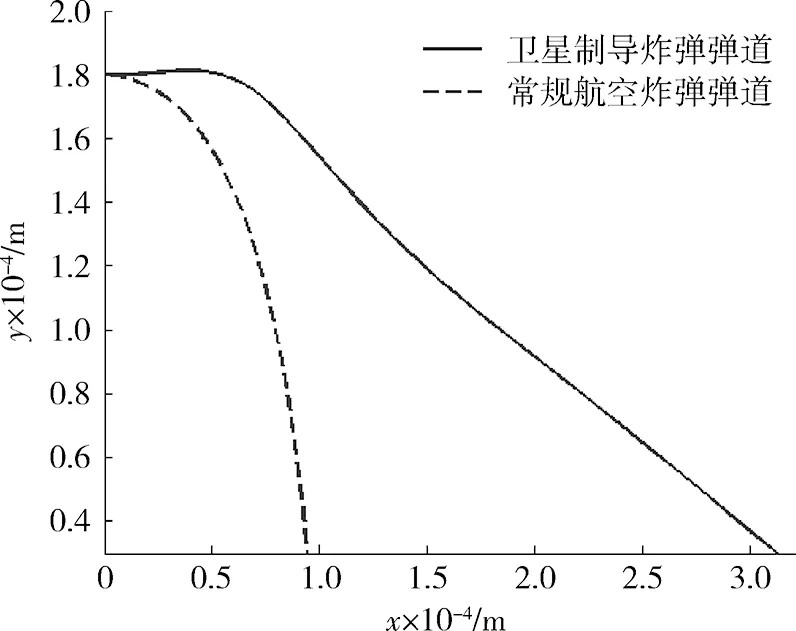
图5 滑翔增程段飞行弹道曲线Fig.5 Flight trajectory of gliding extended range
从图5可以看出:下降至相同高度时,滑翔增程弹道射程是常规弹道在水平方向上的4倍。初始发射时,由于炸弹速度较快,滑翔升力也较大,足以抵消重力的下降作用,弹道出现一段平飞弹道;弹丸平飞时,由于空气阻力的作用飞行速度越来越小,滑翔升力也随之减小,当升力不足以抵消重力时,弹道出现缓慢的下降,但是基本保持着一个稳定的弹道倾角直至增程段结束;可以看到,方案弹道实现了良好的增程效果,表明控制方法是可行的。
4 结束语
在理想条件下建立了制导炸弹滑翔增程段弹道模型,按照滑翔弹道每点升阻比最大原则设计方案弹道,导出了俯仰舵偏角和平衡攻角之间的关系式。通过仿真分析,初始阶段各参数均有不同程度浮动,最终都稳定在理想值附近,得到最优的平衡攻角、舵偏角和飞行速度,滑翔增程效果明显。
[1] 李保平. 航空制导炸弹的发展技术途径与关键技术[J]. 弹箭与制导学报, 2006, 26(3):100-103. LI Bao-ping. The Technical Methods and Key Technology of Air Guided Bombs [J].Joural of Projecties,Rockets,Missiles, 2006, 26(3):100-103.
[2] 肖亮, 王中原, 史金光. 滑翔增程炮弹的气动布局与外形参数优化设计分析[J]. 火力指挥与控制, 2011, 36(3):101-104. XIAO Liang, WANG Zhong-yuan, SHI Jin-guang. Optinizing Design of Aerodynamic Configuration and Parameters for Glide Extended Range Projectile [J]. Fire Control & Command Control, 2011, 36(3):101-104.
[3] 曹红锦, 葛致磊. 滑翔增程弹弹道优化设计研究[J]. 四川兵工学报, 2013, 34(11):8-11. CAO Hong-jin, GE Zhi-lei. A Study on Optimizing Design of Trajectory for Glide Extended Range Projectile [J]. Journal of Sichuan Ordnance, 2013, 34(11):8-11.
[4] 史金光, 王中原, 孙洪辉. 制导炮弹滑翔弹道优化设计方法研究[J]. 南京理工大学学报, 2011, 35(5):100-105. SHI Jin-guang, WANG Zhong-yuan, SUN Hong-hui. Optimization Design Method for Glide Trajectory of Guided Projectiles [J]. Journal of Nanjing University of Science and Technology, 2011, 35(5):100-105.
[5] 白宏阳, 李伟明, 孙瑞胜. 航空时敏制导炸弹增程弹道组合优化设计[J]. 国防科技大学学报, 2014, 36(6):100-105. BAI Hong-yang, LI Wei-ming, SUN Rui-sheng. Trajectory Combinatorial Optimizationdesign for Airborne Time-Sensitive Guided Bombs in Extended Range Period [J]. Journal of National University of Defense Technology, 2014, 36(6):100-105.
[6] 王洪强, 邵晓巍, 杨黔龙. 某型滑翔增程靶弹方案弹道设计[J]. 现代防御技术, 2012, 40(2):27-31. WANG Hong-qiang, SHAO Xiao-wei, YANG Qian-long. Design of Project Trajectory for Glide Range-Extended Target Missile [J]. Modern Defence Technology, 2012, 40(2):27-31.
[7] 陈金明, 耿丽娜, 郑志强. 飞行器最优滑翔弹道研究[J]. 弹道学报, 2009, 21(1):31-34. CHEN Jin-ming, GENG Li-na, ZHENG Zhi-qiang. Study on Optimal Glide Trajectory for Air Vehicle [J]. Journal of Ballistics, 2009, 21(1):31-34.
[8] 蔡德宇. 某型卫星制导炸弹控制系统分析与设计[D]. 哈尔滨:哈尔滨工业大学, 2014. CAI De-yu. Analysis and Design of Guidance and Control System for a Type of Satellite Guided Bomb [D]. Harbin: Harbin Institute of Technology, 2014.
[9] 赵峰, 薛晓东. 一种带角度约束的滑翔弹航向制导律研究[J]. 战术导弹技术, 2015, 14(4):72-76. ZHAO Feng, XUE Xiao-dong. Study of Heading Guidance Law with Angle Constraint for Glide Guided Bomb[J]. Tactical Missile Technology, 2015, 14(4):72-76.
[10] 薛晓东, 刘代军, 王虎峰. 制导滑翔炸弹虚拟比例末制导律研究[J]. 电光与控制, 2013, 20(1):41-43. XUE Xiao-dong, LIU Dai-jun, WANG Hu-feng. Terminal Virtual Proportional Navigation Law for Guided Glide Bomb [J]. Electronic Optics & Control, 2013, 20(1):41-43.
[11] 王旭刚, 王中原, 史金光. 滑翔增程弹制导与控制系统设计[J]. 南京理工大学学报, 2011, 35(3):304-308. WANG Xu-gang, WANG Zhong-yuan, SHI Jin-guang. Guidance and Control System Design for Gliding Extended Range Projectile [J]. Journal of Nanjing University of Science and Technology, 2011, 35(3):304-308.
[12] 谭献忠, 丁则胜, 陈少松. 超远程炮弹滑翔增程机理初步分析[J]. 中北大学学报:自然科学版, 2013, 34(4):398-402. TAN Xian-zhong, DING Ze-sheng, CHEN Shao-song. Preliminary Analysis of the Glide Extended Range Mechanism of the Extreme Extended Range Projectile [J]. Journal of North University of China:Natural Science ed, 2013, 34(4):398-402.
[13] 尚伟烈. 滑翔增程弹气动力计算及分析[D]. 南京:南京理工大学, 2004. SHANG Wei-lie. Calculation and Analysis the Aerodynamic Characteristics of the Glide Bullet[D].Nanjing: Nanjing University of Science and Technology,2004.
[14] 修观, 王良明. 助推-滑翔增程弹弹道优化[J]. 计算机仿真, 2011, 28(12):14-17. XIU Guan, WANG Liang-ming. Trajectory Optimization for Boost Glide Range-Extended Projectile[J]. Computer Simulation, 2011, 28(12):14-17.
[15] 纪京新, 严平, 叶利民. 滑翔增程弹滑翔段弹道设计[J]. 舰船电子工程, 2014, 34(4): 46-48. JI Jing-xin, YAN Ping, YE Li-min. Gliding Trajectory Design of Gliding Extended Range Projectile[J]. Ship Electronic Engineering, 2014, 34(4): 46-48.
Analysis of Glide Range-Extended Trajectory of Satellite Guided Bomb
ZHANG Hui-yong,XUE Zhen, LIU Ze-qian
(Aviation University of Air Force,Jilin Changchun 130022, China)
According to the characteristics of satellite guided bomb’s unpowered flight, in order to extend gliding range, an extension model of glide trajectory of the satellite guided bomb is established, and the glide trajectory is designed by keeping the maximum lift-drag ratio in glide flight. The attack angle is adjusted by controlling the rudder angle, and the upward lift is produced to achieve extended range. The simulation of the glide trajectory shows that the trend of glide trajectory is slow, and the extended range is remarkable.
guided bomb;gild range-extended; trajectory; lift-drag ratio; rudder angle; attack angle
2015-12-26;
2016-03-11
张会勇(1971-),男,吉林长春人。副教授,硕士,主要研究方向为导航、制导与控制。
10.3969/j.issn.1009-086x.2016.06.009
TJ414;TJ765.3
A
1009-086X(2016)-06-0050-04
通信地址:130022 吉林省长春市南关区南湖大路2222号空军航空大学学员11号(薛震收)
E-mail:1012693281@qq.com
