一种基于TLS-STK方法的单站无源定位算法

黄晓刚，徐佳龙，韩雪谦

(海军驻南京地区航空军事代表室, 南京 210002)

·数据处理·

一种基于TLS-STK方法的单站无源定位算法

黄晓刚，徐佳龙，韩雪谦

(海军驻南京地区航空军事代表室, 南京 210002)

文中研究了在存在有色量测噪声情况下的纯方位角单站无源定位问题，给出了一种新的基于总体最小二乘和强跟踪滤波器(TLS-STK)方法的无源定位滤波算法。该算法首先利用总体最小二乘算法进行无源定位，得到初步的目标位置和速度信息，再用这些信息来初始化强跟踪滤波器，最后运用强跟踪滤波器对后续测得的带有色噪声的方位角度值进行滤波，得到高精度的目标定位结果。经过仿真对比实验验证，该算法可较为有效地抑制色噪声的干扰，并具有定位精度高、收敛速度快的特点，能够较好地满足工程实际的应用要求。

有色噪声；无源定位；总体最小二乘；强跟踪滤波器

0 引 言

无源定位是雷达等传感器在无法获得目标的距离、速度等信息的情况下，通过可以测得的目标回波或干扰信号的到达角信息，采用特殊的滤波算法以实现对目标定位的一种技术。由于其具有电磁隐蔽性好、反电子侦察能力强等特点，这种技术在电子情报系统和电子战中，得到了广泛的应用。无源定位系统根据参与的被动传感器的数目，可分为多站无源定位和单站无源定位。本文主要考虑的是单站无源定位问题。

单站无源定位利用机载平台上的测向系统，通过载机平台自身的高阶运动，以及在运动过程中测得的目标的一组方位角测量信息，按照一定的算法进行数据处理，最终获得对目标位置的高精度估值。这里的高阶运动指的是满足系统对辐射源的可观测条件[1]。机载单站无源定位由于具有灵活性好、对系统要求低等优点，受到了各方的特别关注。

目前，单站无源定位技术的实现方法主要有批处理和迭代滤波方法。批处理方法具有不能实时在线估计和运算复杂度高等缺点；而迭代滤波算法对初始值有很强的依赖性，只有当滤波运算的初始估计值在一定的准确度范围内才能有较快的收敛速度。Dogancay[2]提出的基于正交矢量法的总体最小二乘算法(TLS)在系统存在较大的随机观察误差的情况下，也能取得较好的定位精度，但缺点是运算量巨大、实时性差，而且在存在系统误差的情况下，定位精度下降很多。文献[3]提出了一种结合TLS和Kalman滤波的无源定位算法，该算法能比较有效地消除系统误差的影响，但它仅研究了系统误差为恒值常数的情形，而实际中系统误差往往包含有各种形式的误差，并且当不存在系统误差时，该算法性能不如TLS。

针对文献[3]中算法的不足，本文提出了基于总体最小二乘和强跟踪滤波器(TLS-STK)方法的单站无源定位跟踪处理方法。强跟踪滤波器通过强迫滤波器输出的残差序列为近似的不自相关的高斯白噪声序列来消除非恒值系统误差的影响，从而实现目标点的精准定位，可以获得更优的定位效果。

本文首先，介绍了匀速运动目标的基于TLS的纯方位角定位方法；然后，介绍了强跟踪滤波器的实现原理；再次，给出了TLS-STK单站无源定位算法；最后，进行了Monte-Carlo仿真，以验证该算法的有效性和可行性。

1 算法描述

1.1 基于TLS的无源定位算法

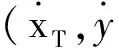
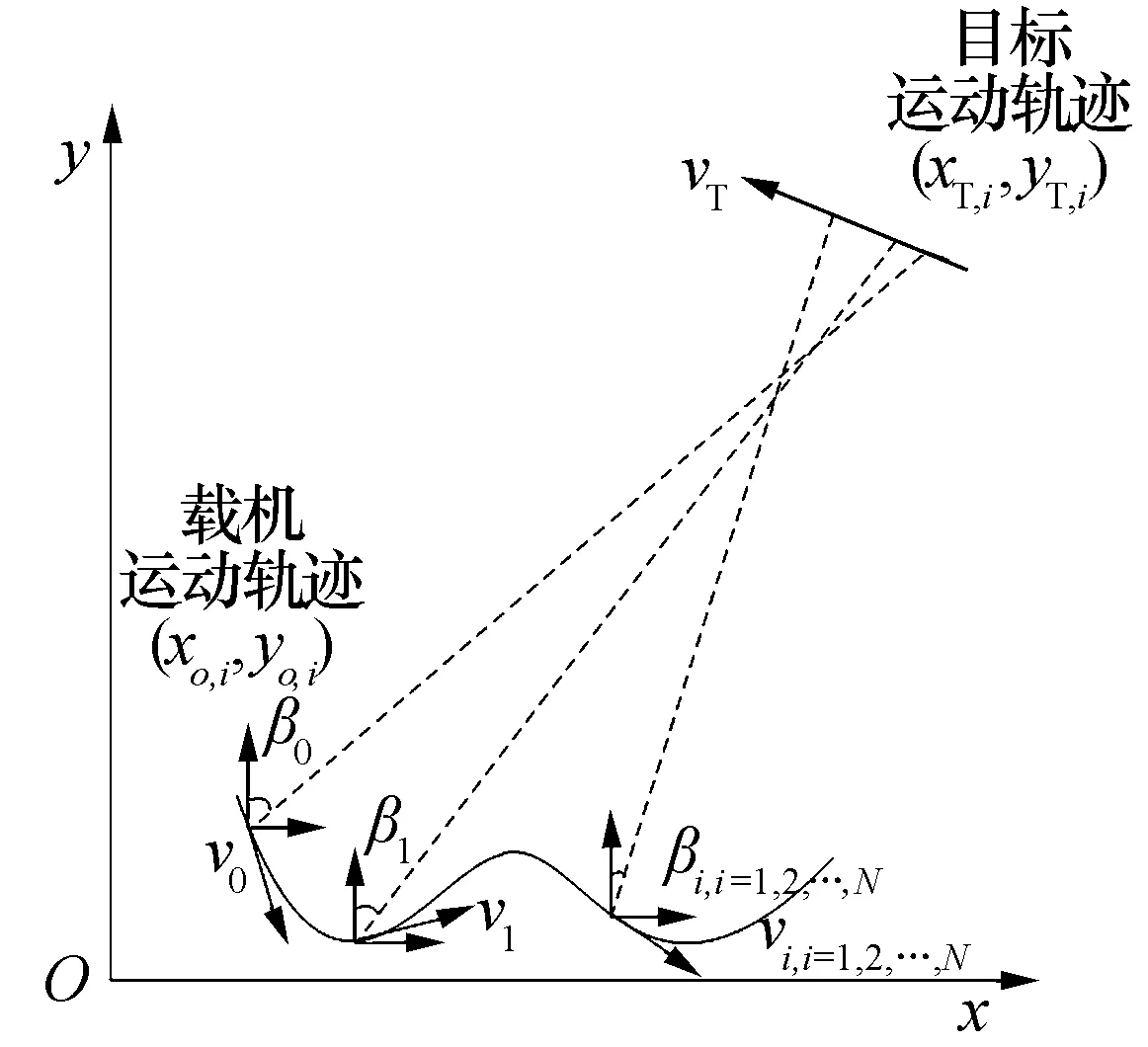
图1 载机与目标之间的几何关系图

由图1的几何关系可知，目标的位置坐标(xT,i,yT,i)满足如下方程

(1)

(2)

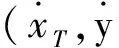
(3)

式中：i=1,2,…,N。为了方便起见，将式(3)转化为矩阵形式

(4)

令

则式(4)可以简写为

HX=Z

(5)

由于方位角观测值βi(i=1,2,…,N)，存在着观测误差，包括随机误差和系统误差。因此，向量Z和矩阵H都存在着扰动噪声。为简化起见，假定向量Z和矩阵H的扰动噪声都是加性高斯白噪声，则可以将式(5)重写成如下形式

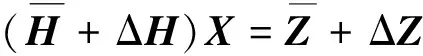
(6)

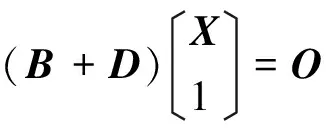
(7)

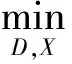
(8)

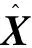
(9)

式中：Vi(5)表示向量Vi的第5个元素。

1.2 强跟踪滤波器

强跟踪滤波器[6-7]通过引入时变渐消因子，在线调节系统增益矩阵，迫使输出残差序列相互正交，使得滤波器具有自适应跟踪状态变化的能力，消除非恒值系统误差对系统滤波结果的影响，从而实现对目标的精准定位。

1.2.1 正交性原理

对于Kalman滤波器(KF)的系统状态估计式

X(k|k)=X(k|k-1)+K(k)[Z(k)-Z(k|k-1)]=

X(k|k-1)+K(k)d(k)

(10)

式中：X(k|k)、X(k|k-1)、K(k)、Z(k)和Z(k|k-1)分别为k时刻的状态滤波值、状态预测值、增益向量、观察值和预测观察值，为d(k)=Z(k)-Z(k|k-1)观测值和预测观察值之间的残差。理想情况下，当模型与实际系统模式完全匹配时，KF(EKF)的输出残差序列d(k)为不自相关的高斯白噪声序列。但在实际滤波过程中，当模型存在较大失配时，输出残差序列不再是处处相互正交。因而，可以通过选择适当的时变增益K(k)，使下列公式成立

E{[X(k)-X(k|k)][X(k)-X(k|k)]T=min

(11)

E{[d(k+j)dT-(k)]}=0，

k=0,1,2,…,m；j=1,2,…,n

(12)

式中：X(k)为k时刻的真实状态向量值；E{}为求期望运算。式(11)是KF(EKF)的性能指标，式(12)要求不同时刻的残差序列处处保持正交。建立在上述条件上的滤波器称为强跟踪滤波器，它通过强迫输出残差近似为高斯白噪声，最大限度地提取输出残差中的有效信息。

1.2.2 强跟踪滤波器的实现

为了实现强跟踪滤波器的特性，需要将时变渐消因子引入一步预测协方差矩阵之中，以削减过去数据对当前滤波值的影响，如式(13)所示

P(k|k-1)=λ(k)F(k-1)P(k-1|k-1)

FT(k-1)+Q(k-1)

(13)

式中：P(k|k-1),F(k-1),P(k-1|k-1)和Q(k-1)分别为k-1时刻的预测协方差矩阵、状态转移矩阵、滤波协方差矩阵和过程噪声矩阵；λ(k)为渐消因子。一种次优的渐消因子λ算法[6]如下

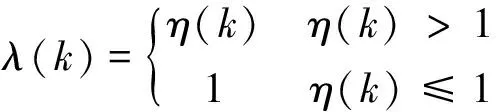
(14)

其中

η(k)=tr[N(k)]/tr[L(k)]

(15)

N(k)=V0(k)-βR(k)-H(k)Q(k)HT(k)

(16)

L(k)=H(k)F(k)P(k|k)FT(k)HT(k)

(17)

V0(k)=E{[d(k)dT(k)]}=

(18)

式中：0≤ρ≤1为遗忘因子，一般取ρ=0.95；d(1)为初始残差；H(k)为k时刻的观测矩阵；R(k)为k时刻的观测误差矩阵；β为衰减因子，根据经验或者仿真设定。

1.3 TLS-STK单站无源定位处理过程

在无源定位的整个过程中，载机都保持做高阶机动，目标机做匀速直线运动。TLS-STK单站无源定位算法的具体实现步骤如下：

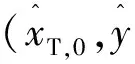
步骤2：利用步骤1算出的目标初始位置和速度值，初始化EKF滤波器和强跟踪滤波器的初始残差d(1)。其中，EKF的初始化协方差矩阵P(0|0)可以初始化为对角阵，即

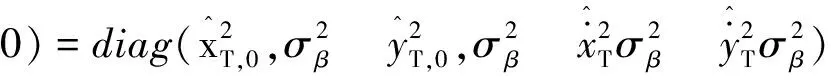
(19)

步骤3：使用目标的角度测量值作为观测值，使用通过强跟踪处理的EKF滤波器对目标的位置和速度做实时滤波，输出滤波结果。

2 仿真实验结果

为验证TLS-STK算法的性能，本文使用Monte-Carlo方法对该算法作了仿真验证，并与EKF算法进行了比较。

载机和目标的运动轨迹，如图2所示。目标机作匀速直线运动，载机作匀速蛇形机动。载机的初始位置在[0km,0km]处，载机的匀速为160m/s，目标相对载机的初始位置为[50km, 55km]，速度为200m/s。载机和目标机作相向飞行，观测周期为1s。

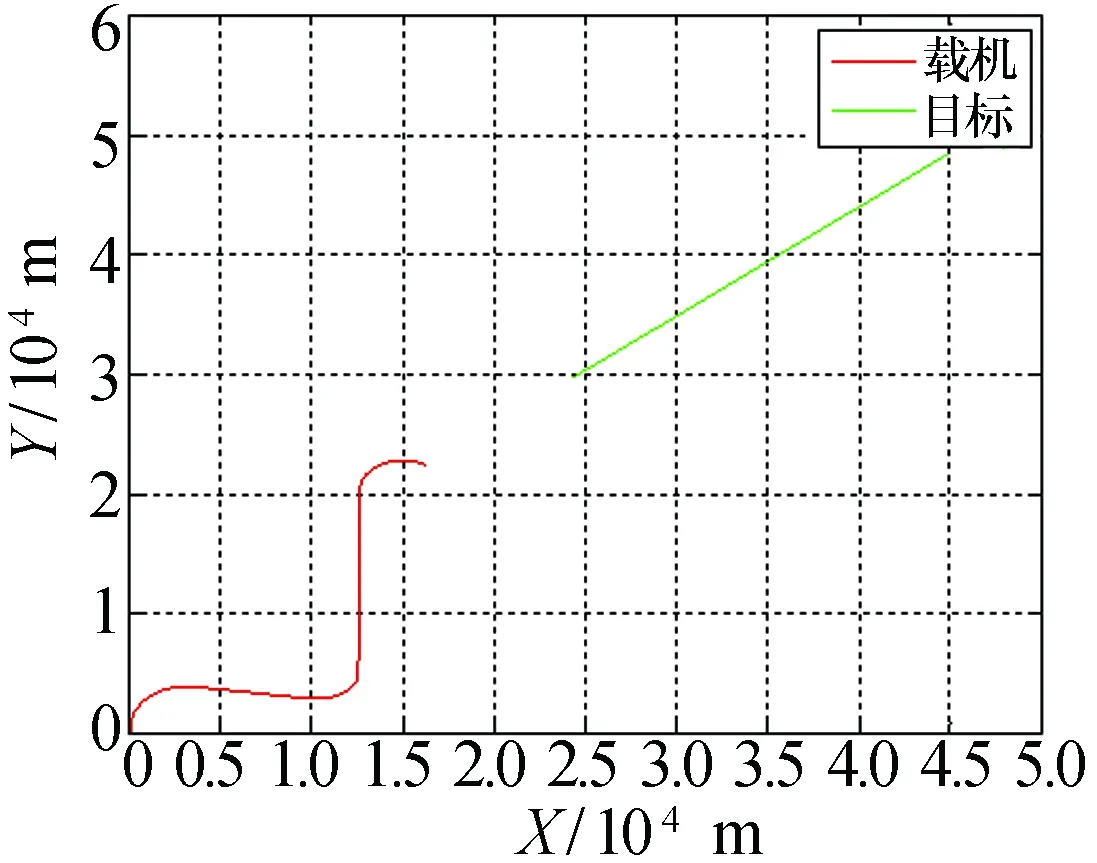
图2 载机和目标的运动轨迹图

我们要仿真的是存在系统偏差的情况下，TLS-STK算法的性能。仿真使用的观测噪声为阶梯高斯白噪声，标准差为0.3°，均值为阶梯函数，如下所示

(20)

经过100次Monte-Carlo仿真试验后，得到TLS-STK和EKF的算法性能对比图，如图3所示。

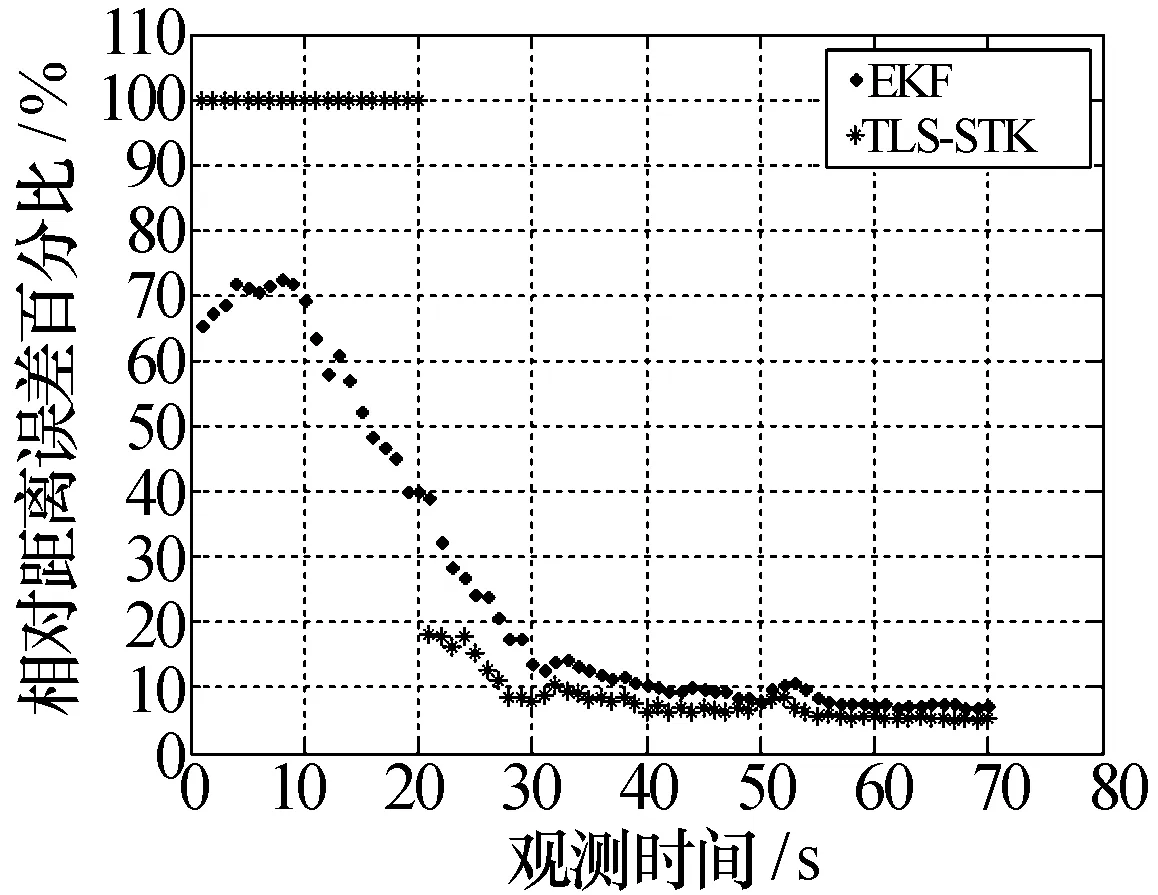
图3 相对距离误差对比图

在TLS-STK算法中，我们使用前20个观测值进行总体最小二乘运算，所以在前20s没有滤波结果输出，误差为100%。在20 s之后，TLS算法有了初步结果，相对误差值发生了跳变，变成了18.2%。从图3可以看出，除了做TLS运算时无结果输出这段时间之外，TLS-STK算法的结果都要明显优于EKF的滤波结果。

3 结束语

本文考虑了存在有色观测噪声情况下的纯方位角单站无源定位问题，给出了一种新的基于TLS-STK方法的无源定位滤波算法。该算法首先利用总体最小二乘算法进行无源定位，得到初步的目标位置和速度信息；然后，用这些信息来初始化强跟踪滤波器；最后，运用强跟踪滤波器对后续测得的带有色噪声的方位角度值进行滤波，得到高精度的目标定位结果。仿真结果表明：在色噪声背景下，该算法收敛速度和滤波精度都比EKF算法要好很多。因此，该算法具有一定的理论意义和实际工程应用价值。

[1] 孙仲康，郭福成，冯道旺, 等. 单站无源定位跟踪技术[M]. 北京：国防工业出版社，2008. SUN Zhongkang, GUO Fucheng, FENG Daowang, et al. Passive location and tracking technology by single observer[M]. Beijing: National Defense Industry Press, 2008.

[2] DOGANCAY K．Bearingsonly target localization using total least squares[J]．Signal Process，2005，85(9)：1695-1710．

[3] RAO K D，REDDY D C．A new method for finding electromagnetic emitter location[J]．IEEE Transactions on AES,1994, 30(4): 1081-1085．

[4] 朱义勇，姚富强，王厚生，等．一种优化的自适应总体最小二乘系统辨识算法[J]．系统仿真学报，2008，20(18)：4843-4846． ZHU Yiyong, YAO Fuqiang, WANG Housheng, et al. Novel variable step-size adaptive TLS algorithm[J]. Journal of System Simulation, 2008，20(18)：4843-4846．

[5] GOLUB G H, LOAN C F V. An analysis of total least squares problem[J]．SIAM Journal on Numerical Analysis, 1980,17(6): 883-893.

[6] 周东华，席裕庚，张钟俊．一种带多重次优渐消因子的扩展卡尔曼滤波器[J]．自动化学报，1991，17(6)：689-695. ZHOU Donghua, XI Yugeng, ZHANG Zhongjun. A suboptimal multiple fading extended Kalman filter[J]. Acta Automatica Sinica,1991, 17(6): 689-695.

[7] 霍 光，李冬海，李 晶．基于强跟踪容积卡尔曼滤波的单站无源跟踪算法[J]．现代雷达，2013，35(11)：52-57. HUO Guang, LI Donghai, LI Jing. A single observer passive tracking algorithm based on strong tracking vubature Kalman filter[J]. Modern Radar, 2013, 35(11): 52-57.

黄晓刚 男，1980年生，工程师。研究方向为雷达军检验收和质量监督。

徐佳龙 男，1969年生，高级工程师。研究方向为航空型号科研、装备订货和管理。

韩雪谦 男，1983年生，工程师。研究方向为雷达军检验收和质量监督。

A New Single Station Bearings-only Passive Target Location Algorithm Based on TLS-STK Method

HUANG Xiaogang，XU Jialong，HAN Xueqian

(Aviation Military Affairs Deputy Office of PLA Navy in Nanjing Zone, Nanjing 210002, China)

The single station bearings-only passive target location problem is studied in this paper in the case of existing colored observation noise, and a new algorithm based on total least squares and strong tracking filter is presented．The algorithm firstly utilizes the total least squares passive target localization method to estimate the primary position and velocity information, then uses this information to initialize the strong tracking filter, finally through filtering the azimuth angle, which takes colored observation noise, to get high precision location information of the target. Simulation results show that the algorithm can restrain the disturbance of colored noise in a certain extent, it also has fast convergence rate and high location accuracy. It is preferable for practical engineering application.

colored noise; passive location; total least squares; strong tracking filter

10.16592/ j.cnki.1004-7859.2016.04.012

黄晓刚 Email：hxgrj2008@163.com

2015-11-02

2016-01-08

TN971

A

1004-7859(2016)04-0050-04