基于时频图的飞机目标特征提取算法

姜 悦，范菊平，郭乐田，邓广健

(西北核技术研究所 高功率微波重点实验室, 西安 710024)

·信号处理·

基于时频图的飞机目标特征提取算法

姜 悦，范菊平，郭乐田，邓广健

(西北核技术研究所 高功率微波重点实验室, 西安 710024)

研究了两种基于时频分析的飞机目标特征提取算法。首先，介绍利用短时傅里叶变换获得目标二维时频图信息，然后，分析飞机目标回波时频图的图像熵特征和平均时频谱特征，给出了这两种特征的提取算法，仿真得到利用这些特征对三类飞机的分类识别结果，分析了其目标分类识别性能以及适用情况。在研究时频图平均时频谱特征提取算法时，发现单独使用此特征在飞机目标分类识别中存在的问题，加入基于平均时频谱的方差特征，综合两种特征实现了对三类飞机目标的的分类识别。仿真结果表明，这两种特征的目标识别正确率都能达到94%以上。

特征提取；微多普勒；短时傅里叶变换；时频图

0 引 言

空间目标探测、识别和监视能力体现了一个国家的空间力量和空间战略，是国家战略力量的重要组成部分。近几年来的多场局部战争表明，空间已经成为战场整体形势感知和信息夺取优势的“制高点”。能够准确检测、识别空间飞机目标，提早进行规避或打击，全面掌握制空权，这些对于现代战争来说至关重要。

目标回波的时频图包含了大量的目标物理信息，针对如何利用其提取目标有效特征进行分类识别分别在文献[1-4]中有所描述。就时频图区别于目标回波信号的二维性而言，仅从时频图图像域的角度考虑，就存在着不同的目标特征提取方法。本文提出的两种基于时频图的飞机目标特征提取算法，分别从时频熵角度和图像维角度，对三类飞机目标进行特征提取和分类。

1 短时傅里叶变换时频图

本文给出的两种目标特征提取算法均是基于目标时频图信息的，因此，应用这两种算法的首要条件就是获得合适的时频图。

飞机目标旋转部件对雷达信号的响应相当于一个非线性系统，其雷达回波信号具有非线性和非平稳的特点。简单的傅里叶变换无法对雷达回波信号进行全面的分析，为了获取更多信号相关信息，需要将一维信号映射到二维时频平面，因此引入了短时傅里叶变换(STFT)[4]对信号进行时频域处理，得到目标时频图信息。

STFT的基本思想是利用窗函数来截取信号，并假定信号在截取窗内是平稳的，再采用傅里叶变换分析窗内信号，然后沿着信号时间方向移动窗函数，得到整个信号频率随时间的变换关系，即所需要的时频信号x(t)的短时傅里叶变换可以表示为

(1)

式中：x(t)为被分析信号；g(t)为窗函数。

反变换为

(2)

信号的短时傅里叶变换在很大程度上受窗函数的影响。窗函数的选择一般需要考虑两个因素：第一是信号泄漏，窗函数选择的越短，信号泄漏就越严重；第二是窗函数的窗口特性，不同的窗函数拥有不同的窗口特性，而高斯窗函数则具有最好的时频特性。

短时傅里叶变换在一定程度上弥补了常规傅里叶变换不具有局部分析能力的不足，但同时也存在一些自身无法克服的缺陷。当窗函数确定之后，时频窗的形状和大小就确定了，其时频分辨率也确定了，分辨精度在整个相平面内都是一致的，不具有随着信号频率变化的自适应能力。因此，选择合适的时频窗函数长度十分重要，太短的时频窗函数长度会造成出现高频假象，而太长的时频窗函数长度则会造成不同时刻频率的重叠出现混频现象，达不到时频分析的目的。

2 图像熵特征提取算法

2.1 时频图的熵特征

直升机、螺旋桨飞机和喷气式飞机三类目标空间微动部件回波经短时傅里叶变换得到的时频图在图像域上存在明显差异。图1绘制了三类飞机实测数据的时频图。

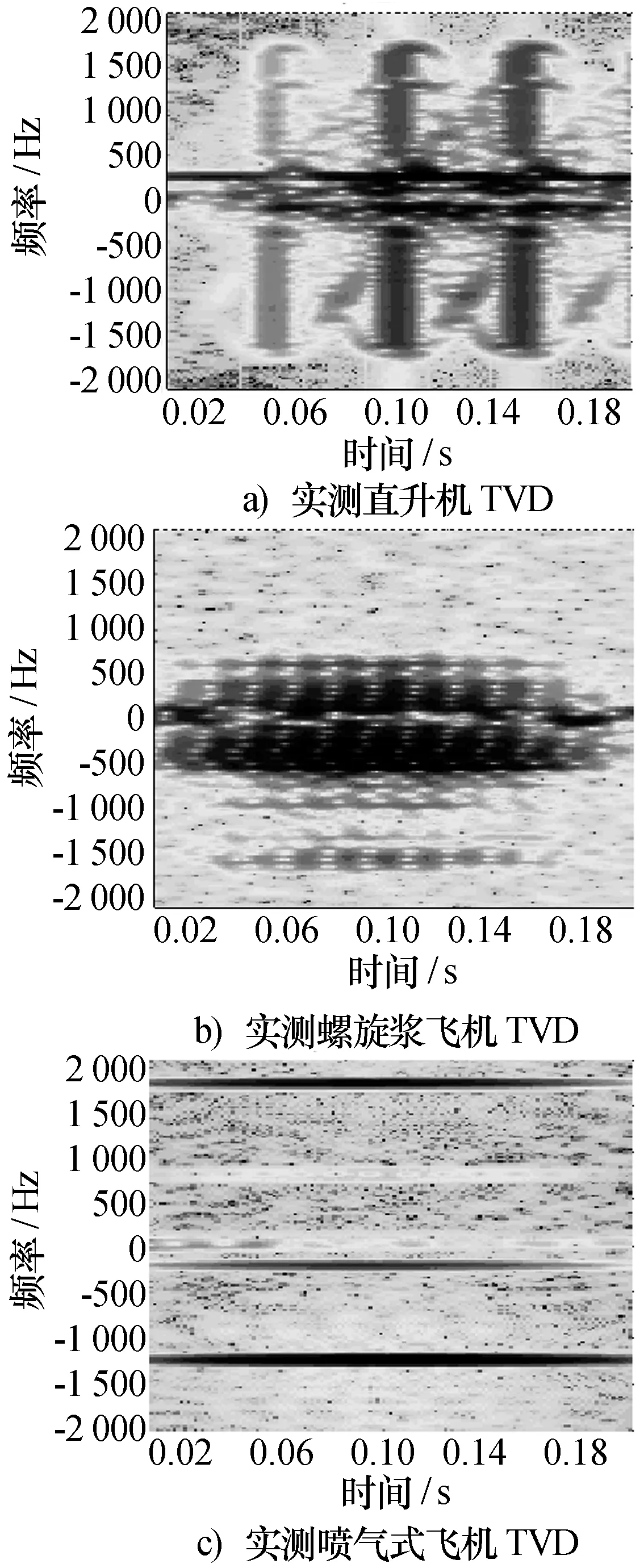
图1 三类飞机实测数据时频图

对目标的时频图而言，不同亮度的像素点代表了不同的信号幅度，不同的目标就会表现出不同的形状，而这些图像所包含的信息量是不同的。按照统计学的观点，由于图像分布具有块状结构，因此，各像素点具有位置上的相关性，可以用信息熵来描述图像形状。时频图属于二维数据，并且时频图图像数据具有非负性，即f(x,y)≥0，对于M×N维的时频图，定义图像熵[5]H(f)为

(3)

图像熵H(f)反映了时频图信息量的大小，可以描述其幅度分布信息。当图像比较尖锐、清晰时，时频图中频点幅度会有剧烈变化，此时图像包含的信息量多，图像熵值小；当图像比较模糊时，图像灰度值变化比较平滑，时频图中各频点幅度变化缓和，图像信息量少，图像熵值大。因此，可以根据三类飞机目标图像熵的差异，作为对目标进行分类识别。

2.2 仿真分析

根据时频图图像熵的定义计算得到直升机、螺旋桨飞机和喷气式飞机的图像熵值分布，如图2所示。

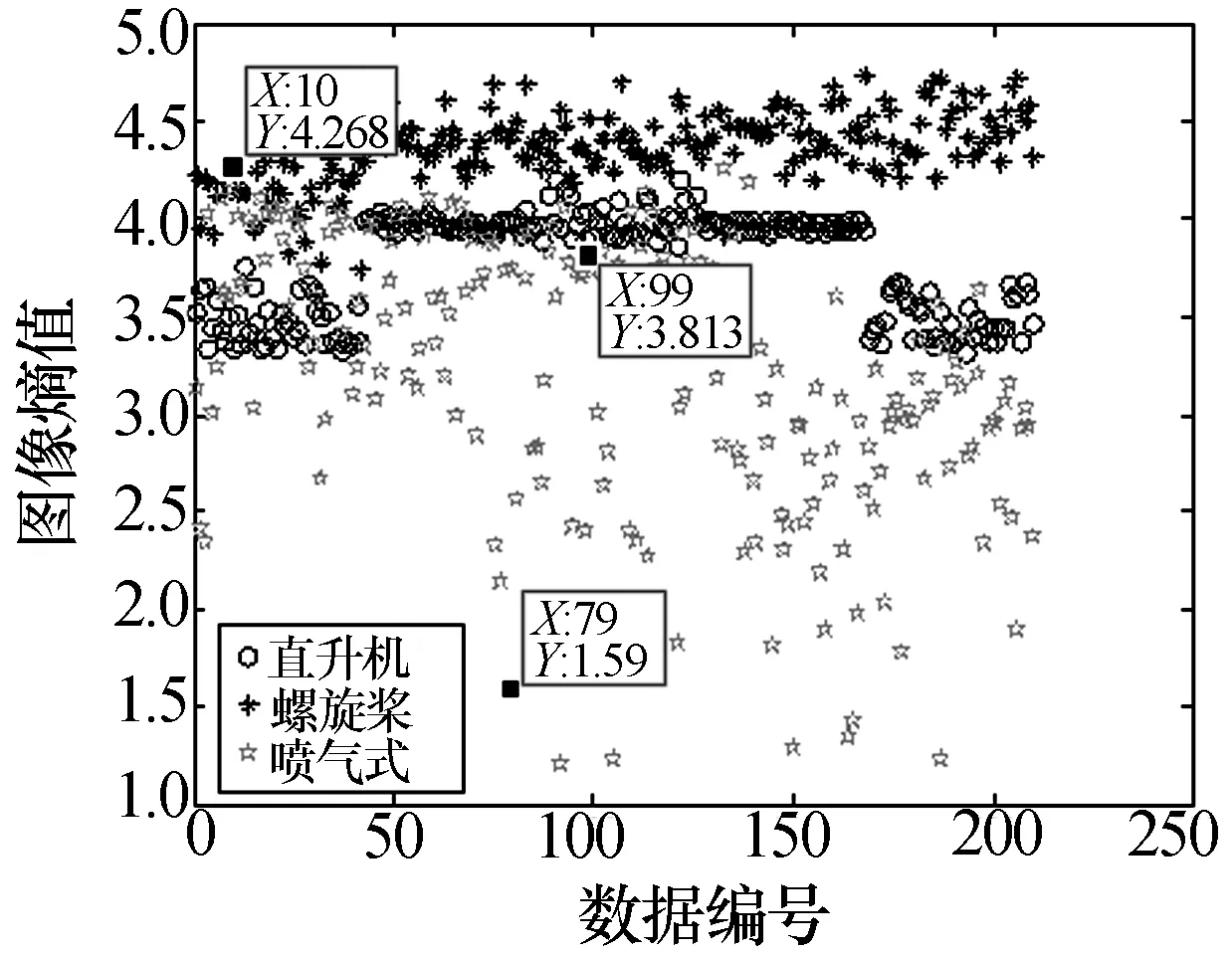
图2 仿真三类飞机目标图像熵散布图

可以发现三类飞机图像熵值的分布区域化明显，不同目标之间存在明显的分类界面。直升机与喷气式飞机的图像熵值区别较大，它们之间不存在共用熵值区间的情况。螺旋桨飞机的图像熵值处在另外两类飞机目标之间，在某些飞行姿态和旋翼转速下存在错分的情况。仿真产生雷达重频为4 kHz，驻留时间0.15 s的训练数据共630组，测试数据为三类飞机各100组。SVM分类器对上述飞机目标的分类识别结果如表1所示。

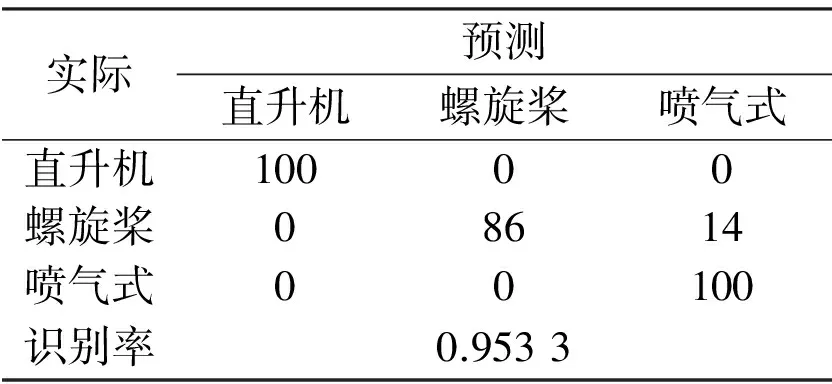
表1 仿真数据分类结果的混淆矩阵

3 平均时频谱特征提取算法

3.1 时频图的平均时频谱特征

目标回波的时频图M(t,f)，反映了任意时刻目标各散射点的瞬时多普勒频率。由于目标上存在多个散射点，其时频谱是所有散射点时频谱的线性叠加，所以可以通过以下函数表征其瞬时频率的平均值

(4)

对于离散信号，可以直接将上式离散化，得

(5)

式中：f(t)表征了目标各散射点瞬时多普勒频率的期望，是各散射点瞬时多普勒频率的线性组合。对f(t)做傅里叶变换[6]，得到的频谱包含了目标回波瞬时多普勒频率所有的频率分量。这里把f(t)经过傅里叶变换得到的频谱称为平均时频谱。图3分别描述了三类飞机目标的典型平均瞬时多普勒频率f(t)，以及f(t)经过傅里叶变换后的平均时频谱。

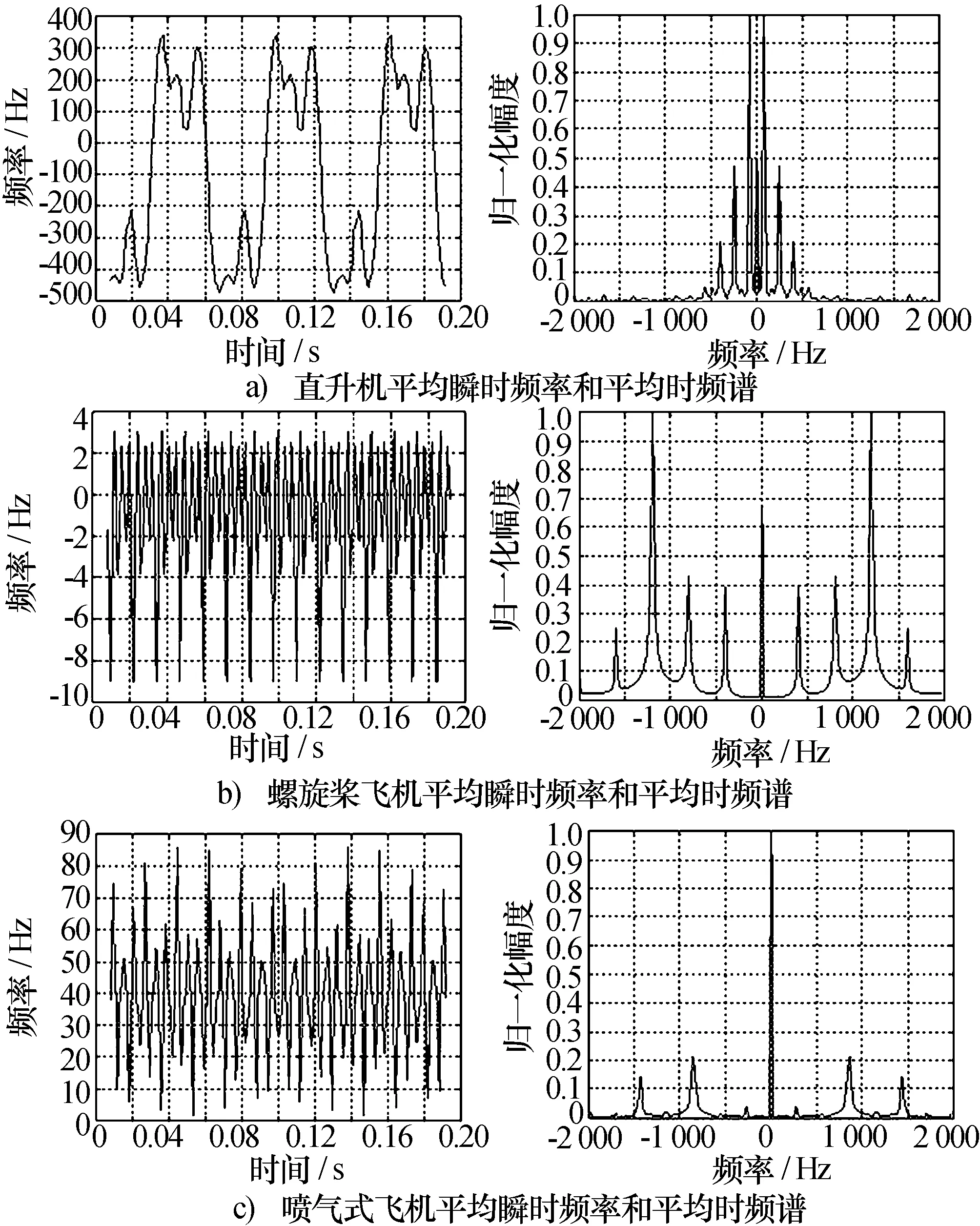
图3 仿真三类飞机平均瞬时频率和平均时频谱

飞机目标的平均时频谱在处理过程中涉及两次傅里叶积累。第一次是为了得到目标回波时频图，第二次则是为了得到目标的平均时频谱，所以飞机目标平均时频图对噪声并不敏感。

观察图3可以发现，直升飞机平均时频谱谱线峰值最多，峰值分布密集；螺旋桨飞机的谱线明显峰值较少，并且峰值分布较为稀疏；喷气式飞机的仅在零频处存在明显峰值，其余谱线都很小。根据以上特点可以提取了两种散布特征，一种是f(t)的频谱部分区间的熵值，称之为平均时频谱的波形熵特征；另一种是f(t)的频谱谱线的方差，称之为平均时频谱方差特征。两种特征的数学表达式如下：

特征一：平均时频谱波形熵[7]

(6)

式中：pi表示所选f(t)的频谱区间内频点i的归一化能量；

特征二：平均时频谱方差

(7)

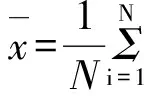
3.2 仿真分析

平均时频谱的波形熵特征已经能够较为明确地描述三类不同飞机目标之间的差异，但是在实际分类识别中发现，在某些飞机飞行姿态和旋翼转速下喷气式飞机的平均时频谱的波形熵特征会与其他两类飞机产生混淆，造成识别错误。图4为三类飞机目标平均时频谱特征的散布图，可以发现其中有部分喷气式飞机的熵值跳动明显。

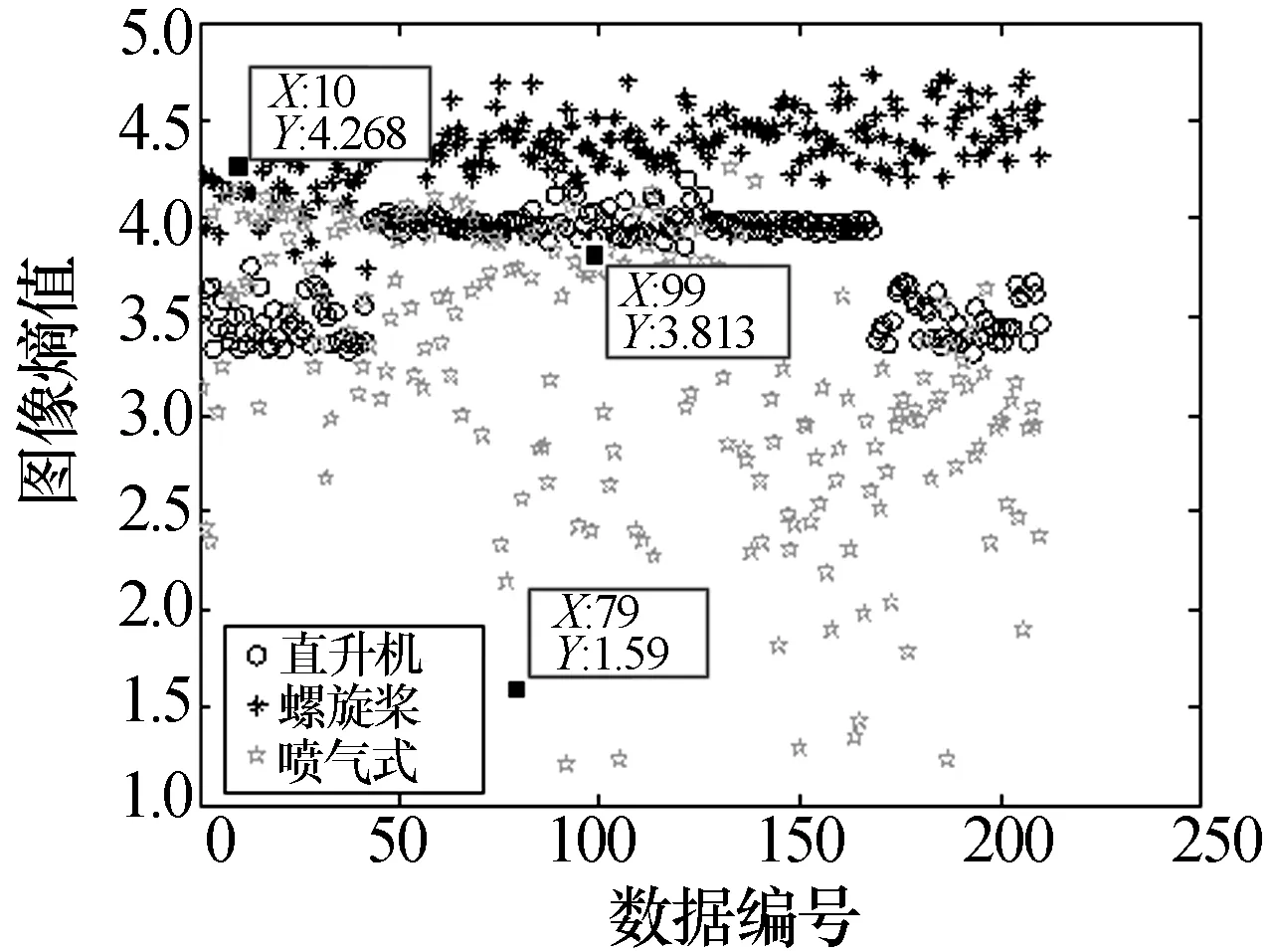
图4 仿真三类飞机目标平均时频谱波形熵特征散布图

为了分析喷气式飞机平均时频谱波形熵值差异明显的原因，选取具有代表性的三组数据：第10组、第79组、第99组，观察其时频图以及平均时频谱的特点。分析发现，喷气式飞机由于其旋翼处于涵洞内并且尺寸较小，目标回波中飞机机身分量能量较强，在某些飞机飞行姿态下更是无法得到明显的旋翼回波，造成这类回波数据与能够明显观察到旋翼回波的数据在时频图以及平均时频谱上都存在明显不同，最终导致平均时频谱波形熵特征在识别此类数据上的“失灵”。图5描述了平均时频谱波形熵差异明显的三组喷气式飞机数据的时频图和平均时频谱，其中第10组数据肖似螺旋桨飞机，第99组数据肖似喷气式飞机。因此，为了能够区分上述喷气式飞机数据，引入了平均时频谱方差特征，使用这两类特征同时对飞机目标进行分类识别。

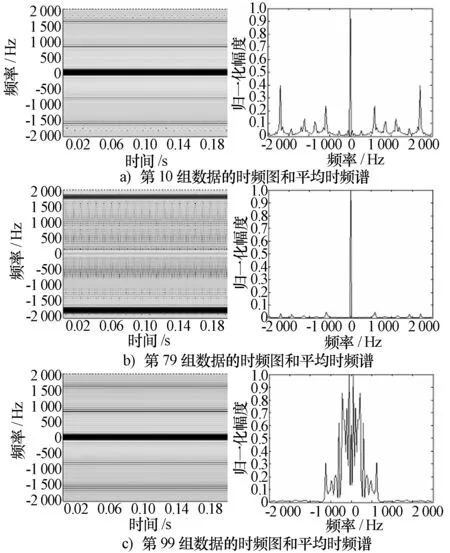
图5 喷气式飞机典型数据的时频图及平均时频谱

图6构建了以平均时频谱波形熵特征及其方差特征为坐标的特征平面[8]，画出了仿真三类飞机目标数据的特征分布情况。加入了平均时频谱方差的二维特征能够更好的区分三类飞机。

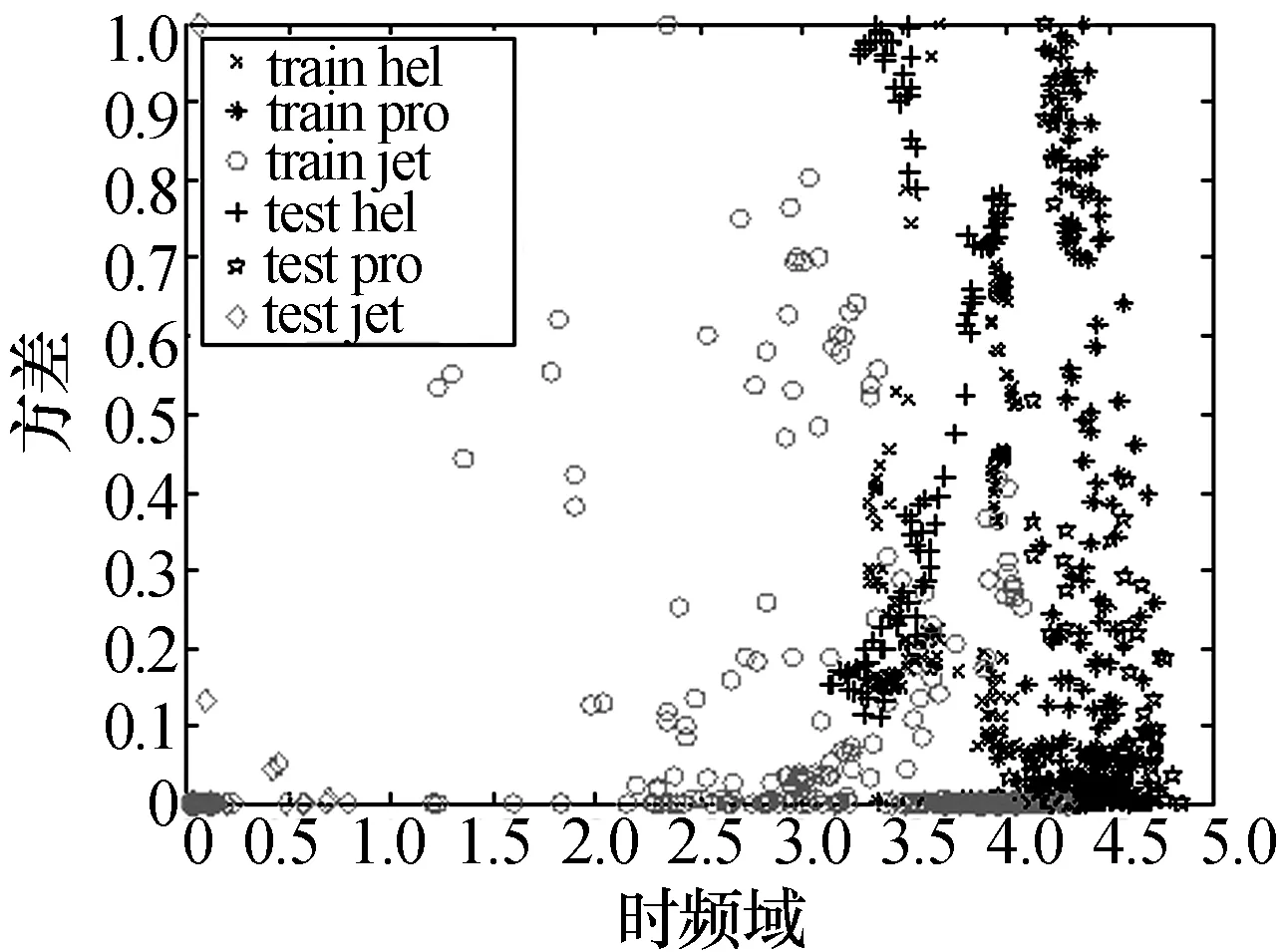
图6 仿真三类飞机平均时频谱波形熵、方差二维特征散布图

表2为三类飞机仿真数据，利用SVM分类器的分类结果，可见分类识别效果明显。

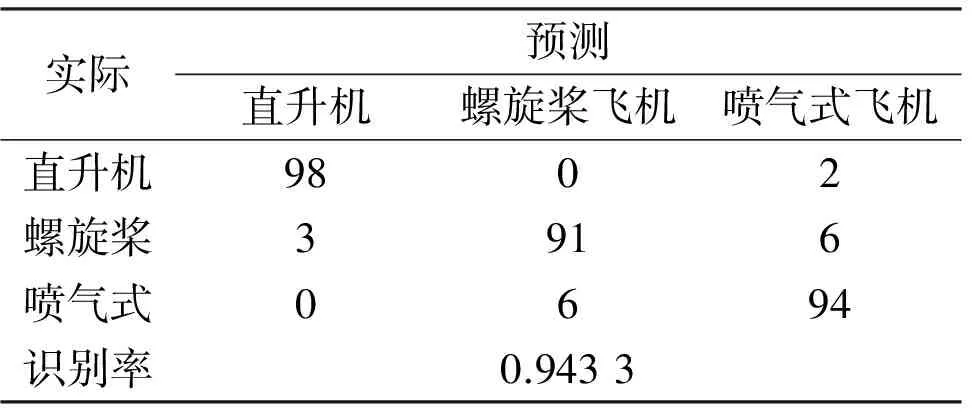
表2 仿真数据分类结果的混淆矩阵

4 结束语

针对目前窄带雷达接收到的目标回波，为了得到更多的信息，从目标回波时频图中提取目标特征对目标识别研究有重要价值和意义。本文所述的两种特征提取方法，分别从目标回波时频图的图像角度和信号角度处理了目标微多普勒回波数据，表明时频图在提取目标特征时存在多种选择。

[1] BOASHASH B. Time-frequency siganl analysis and processing[M]. Amsterdam: Elsevier Ltd. 2003.

[2] 崔 瑞，薛 磊. 基于图像熵的逆合成孔径雷达干扰效果评估方法[J]. 现代防御技术，2009,37(1): 94-97. CUI Rui, XUE Lei. Evaluation method of jamming effect on ISAR based on image entropy[J]. Modern Defence Technology, 2009, 37(1): 94-97.

[3] 王 璐. 微动目标的运动参数估计和识别方法研究[D]. 西安：西安电子科技大学，2010. WANG Lu. Research on parameter extraction and recognition of target with micro-motion[D]. Xi′an: Xidian University, 2010.

[4] PETERSSON H, BJORKLUND S, KARLSSON M, et al. Towards surveillance using micro-Doppler radar[C]// International Radar Symposium. Hamburg, Germany: IEEE Press, 2009: 9-11.

[5] 刘志成，何佳洲. 多普勒频谱及JEM效应在空中目标识别中的应用分析[J]. 指挥控制与仿真, 2009, 31(1): 38-41. LIU Zhicheng, HE Jiazhou. Analysis of Doppler spectrum and JEM effect in air target recognition[J]. Command Control & Simulation, 2009, 31(1): 38-41.

[6] BJORKLUND S, JOHANSSON T, PETERSSON H. Evaluation of a micro-Doppler classification method on mm-wave data[C]// IEEE Antennas and Propagation Society International Symposium. [S.l.]: IEEE Press, 2012.

[7] 王盛利. 雷达信号处理的新方法——匹配傅里叶变换研究[D]. 西安：西安电子科技大学，2003. WANG Shengli. Study on new radar signal processing——matched Fourier transform[D]. Xi′an: Xidian University, 2003.

[8] CAI Chengjie, LIU Weixian, FU J S, et al. Empirical mode decomposition of micro-Doppler signature[C]// Proceedings of International Conference on Radar. Washington, USA: IEEE Press, 2005: 895-899.

姜 悦 女，1989年生，硕士研究生。研究空间微动目标识别和目标微多普勒特征提取方法。

Feature-extraction Algorithm of Airplane Targets Based on Time-Frequency Diagram

JIANG Yue，FAN Juping，GUO Letian, DENG Guangjian

(Northwest Institute of Nuclear Technology, the Science and Technology on High Power Microwave Laboratory, Xi′an 710024, China)

Two target feature extraction of airplane is mainly studied by time-frequency diagram(TFD). The first part based on airplane backscatter TFD , which comes from STFT, two algorithms for airplane are proposed and studied, one of them using target image entropy characteristics, anther using average time-frequency entropy and variance characteristics. As the same time, the merits and drawbacks of this method has been simulated and explained. This two feature have effective detection performance, the correctly rate all above 94 percent.

feature extraction; micro-Doppler; STFT; time-frequency diagram

10.16592/ j.cnki.1004-7859.2016.04.009

姜悦 Email：jwjbetty2008@163.com

2015-11-02

2016-01-12

TN911.7

A

1004-7859(2016)04-0038-04