基于单目视觉的实时测距算法

2016-02-23盛海军王华强

宿州学院学报 2016年8期

关键词：单目畸变测距

赵松，盛海军，王华强

1.安徽水利水电职业技术学院机电工程系，安徽合肥，231603 2.合肥工业大学电气与自动化工程学院，安徽合肥，230009

基于单目视觉的实时测距算法

赵松1，盛海军1，王华强2

1.安徽水利水电职业技术学院机电工程系，安徽合肥，231603 2.合肥工业大学电气与自动化工程学院，安徽合肥，230009

为了利用单目视觉实时测量室内移动目标与障碍物之间的距离，在比较了现有的几类用于智能监测的深度信息获取方法的基础上，提出了基于单目视觉的实时测距算法。首先根据小孔成像原理，得到成像点和目标点的映射关系，建立针孔模型。然后通过成像点与目标点的空间几何关系，获取图像的深度信息。为了验证单目视觉的实时测距算法的准确性，将算法结果与实验结果进行了比较。实验结果显示，此算法可以满足智能监控的实时性要求。

单目视觉；深度信息；针孔模型；实时测距

随着智能视频的发展，通过视觉获得运动目标的位置信息已经是智能视频技术领域的一个热点问题。因为视觉定位与其他定位方法相比，具有结构简单、获得信息直观、非接触性等特点[1-3]。目前，视觉定位按视觉传感器的数目分为两类，即单目和多目。单目视觉定位是采用一个视觉传感器应用小孔成像原理来获得运动目标的深度信息，而多目视觉定位是采用多个视觉传感器的立体匹配来获得运动目标的深度信息。在多目视觉中，特征点的立体匹配是难点，选择什么准则来限制搜索空间和自动去除不适合的匹配特征，对其应用场合有一定的限制；而用单目视觉定位，则避免多目视觉中的立体匹配问题，并能提高实时性。

本文在目标检测和跟踪基础上提出一种基于单目视觉的运动目标定位算法，即基于小孔成像模型，运用空间几何关系得到像素坐标系和世界坐标系之间的转换关系，较好地解决了传统单目视觉定位方法根据目标中特征信息来定位容易受遮挡和光照影响问题。

1 摄像机的成像模型

摄像机成像的原理是利用光电耦合传感器将实际的模拟信号转化为数字信号，每幅数字图像由M×N个元素组成，每个元素表示一个像素，每个像素点值的大小表示图像中该点的灰度或亮度与M×N个光电耦合单元上的电荷量相等。实际上就是将现实中三维空间的景象映射到二维空间的过程，可以采用四个坐标系来表示这种映射关系[4-6]，这四个坐标系如图1所示。

图1 摄像机成像坐标系

从图1可以得到摄像机成像模型是线性的针孔模型，可以推导出从三维(世界坐标系)到二维(像素坐标系)的转换公式：

(1)

其中，ax=f/dx,ay=f/dy。

2 视觉图像的非线性畸变模型

摄像机所采集的图像与理想模型(小孔成像模型)之间是有误差的，表现为图像中像素点的位置，一般将这种误差称作为图像的非线性畸变，主要包括径向畸变、薄透镜畸变、偏心畸变三种。这是由于实际成像设备在制造和装配过程中的缺陷以及透镜本身折射形成的误差等造成的。图像中的非线性畸变是由这三种畸变的叠加，如下式：

(2)

(3)

其中，k1,k2,p1,p2,s1,s2是非线性畸变系数，因为高阶分量会造成求解的不稳定，所以建模时不考虑，故在本文只考虑非线性畸变中的切向和径向畸变。

3 摄像机的标定

运用公式(2)建立空间点从三维(世界坐标)到二维(像素坐标)的转换关系，摄像机的内参数矩阵是由其自身决定的，而外部参数矩阵则由其位置和姿态决定。本文中使用的摄像头是分辨率为704×576，焦距为8mm，成像尺寸为1/3，且带有红外夜视功能。首先绘制一张5×8平面棋盘格，如图2所示。

图2 5×8平面棋盘格

摄像头的畸变参数：

k1=-0.2675,k2=-0.8467

p1=0.00312,p2=0.00782

摄像头的内参数矩阵M：

4 实时测距算法推导和验证

为了利用单目视觉实时监测室内移动目标与障碍物之间的距离，在比较了现有的几类用于智能监测的深度信息获取方法基础上，提出了基于单目视觉的实时测距算法。根据小孔成像原理，得到成像点和目标带点的映射关系，建立线性模型，然后利用成像点与目标点的几何关系，对计算结果进行畸变校正，获取图像的深度信息。实验结果显示，该算法具有较高的准确性，满足测距要求，且该算法计算量小，能满足智能监控的实时性要求。其针孔模型如图3所示[7-8]。

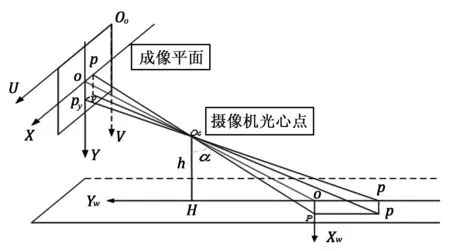
图3 针孔模型

图3中，P是世界坐标系平面上任意一点，Px是P点在世界坐标系Xw轴上的投影，Py是P点在世界坐标系Yw轴上的投影，其中：f=O1Oc为CCD摄像机的有效焦距;α为固定CCD摄像机的俯仰角度;H是为摄像头光心Oc在世界坐标系的投影点；h为实际测量取得的摄像头光心Oc离地面的距离，等于OcH长度。

根据空间几何关系得到任意一点P与摄像头的水平距离HPy(即Dy)的计算公式：

Dy=h×tan(α+β)

(4)

其中，h和α待摄像头固定后，可以直接测得；β是线段Pypy与光轴O1Ow相交形成的夹角∠O1Ocpy(或∠PyOcOw)，所以在直角三角形ΔO1Ocpy中可得：

(5)

由于O1py=py，O1Oc=f，所以在直角三角形ΔO1Ocpy中可得：

(6)

联立公式(4)(5)(6)可得：

(7)

同理：

Dx=h×tanγ/cosα

(8)

(9)

联立公式(7)(9)可得：

(10)

其中，O1px=px。

由公式(2)可得，目标点在像素坐标系的坐标转换到成像平面坐标系下的坐标：

(11)

联立公式(13)(14)可得在线性模型下，摄像头到地面上任意一点P的水平距离：

(12)

图4 目标点在像素坐标中修正前后的坐标

根据上述实验结果可知，离光心越近的目标，其畸变越小，反之，目标畸变越大。

本算法计算结果的精度受以下两个因素影响：一是摄像头的安装高度h是否准确，二是计算摄像头安装俯视角α是否精确。通过改变摄像头的高度h，但保持摄像头的俯仰角α=64.9°和其他参数不变，得到因素一对距离计算结果精度的影响，如表1所示。

表1 随高度变化的距离

然后改变摄像头的俯仰角α，但保持摄像头的安装高度h=19.1cm和其他参数不变，得到因素二对距离计算结果的影响，如表2所示。

表2 随俯仰角度变化的距离

对上述实验数据进行分析，可以得到：当摄像头的高度变化范围为8cm时，引起的距离变化为24cm；而当摄像头的俯仰角变化范围为0.4°时，引起的距离变化为104cm。由此可见，摄像头安装高度对求解距离的精度影响较小，相比而言，摄像头俯仰角对求解距离的精度起至关重要的作用，在很大程度上制约物体到摄像头的距离求解的准确性，所以对初始俯仰角α要进行多次测量，取其平均值。

为了进一步验证该算法的精确度，对摄像头采集到的一段动态视频中移动目标进行定位，实验参数：摄像头的高度h=28.2cm，俯仰角α=64.9°，H点与前方障碍物体距离依次递增为90、105、140、150cm。摄像头识别的障碍物(本实验中障碍物为一个墨水瓶)图像和测距结果如图5和表3，图中识别的目标用矩形框标出。

图5 摄像头识别、跟踪的障碍物图像

实际距离Dr/cm测量距离Dm/cm误差/%9083.447.310599.844.9140143.032.2150159.756.5

实验结果显示，摄像头与障碍物的距离在105～140cm范围时，本文算法的测量误差控制在5%范围内；当距离为90cm时，误差稍大，为7.3%。因此，在实际距离为105～140cm范围内，测量距离与实际距离差值不超过6cm，故本文提出的测距算法可以满足利用机器视觉进行障碍物的检测和距离计算准确性的要求。