循环荷载下滨海软粘土累积塑性应变试验研究

王元战，胡珅榕，杨攀博

（1.天津大学水利工程仿真与安全国家重点实验室高新船舶与深海开发装备协同创新中心，天津 300072；2.中交第一航务工程勘察设计院有限公司，天津300222）

循环荷载下滨海软粘土累积塑性应变试验研究

王元战1，胡珅榕1，杨攀博2

（1.天津大学水利工程仿真与安全国家重点实验室高新船舶与深海开发装备协同创新中心，天津 300072；2.中交第一航务工程勘察设计院有限公司，天津300222）

近海工程在波浪等循环荷载的作用下，地基中的软粘土会产生较大的沉降和变形，影响上部结构的稳定性。本文以烟台港的淤泥质粘土为研究对象，进行动三轴试验，以围压、静偏应力、动应力、荷载循环次数等为变量，探讨了不同工况下淤泥质粘土的累积塑性应变发展规律。试验结果表明，累积塑性应变随着荷载循环次数的增加，先迅速增大，而后增速减缓，最终应变值趋于稳定；累积塑性应变受不同围压值的影响不明显，但是静偏应力比、动应力比越大，其初始增速越快，最终达到的稳定值越大。通过试验结果分析，综合考虑围压、静偏应力、动应力、荷载循环次数等影响因素，提出能够合理描述累积塑性应变发展规律的双曲模型，并应用于烟台港实际工况，计算结果符合工程实际。

软粘土；循环荷载；累积塑性应变

我国沿海地区普遍分布着含水量高、孔隙比大且强度较低的软粘土地基。近些年来，随着经济社会的发展，近海工程日趋大型化、深水化、复杂化，对地基稳定性的要求日益提高，而地基土体在波浪循环荷载作用下的沉降和变形问题也日益突出。如1999年，辽东湾JZ9-3系缆平台的沉箱式基础在安装过程中经历风暴潮，沉箱产生1.7 m沉降，因及时用桩固定，才避免了事故进一步恶化［1］。因此，研究软粘土在循环荷载下的累积塑性应变发展规律，具有十分重要的意义。

国内外学者针对累积塑性应变的发展规律做过很多研究。Monismith等［2］通过不同应力水平的动力试验，提出累积塑性应变随循环次数发展的指数模型，并指出不同的应力路径会对累积塑性应变产生影响；Chai和Miura等［3］则在Monismith指数模型的基础上，引入静偏应力和动应力这两个影响因素，对该指数模型进行了修正；Hyodo等［4］通过正常固结饱和粘土的动力试验，提出考虑初始静偏应力影响的长期循环荷载下的粘土累积塑性应变模型，并指出粘土的弹性应变与其有效应力之间存在一定的函数关系；闫澍旺等［5］通过正常固结软粘土的动力循环试验，提出累积轴向应变与归一化累积孔压之间存在唯一的对应关系，而与加载方式、振动频率等因素的关系不大；王建华等［6］根据软粘土的固结不排水动三轴试验结果，分析了动变形等向弱化的力学特性，并提出了轴向塑性应变的计算模型；王军等［7］进行了杭州原状软粘土的双向激振三轴试验，并分析了初始剪应力、固结围压和加载速率等因素对粘土动力变形特性的影响；王常晶等［8］通过萧山原状饱和软粘土的循环三轴试验，得出了静偏应力对累积塑性应变的发展影响显著，静偏应力越大，塑性应变发展越快；黄茂松等［9］通过上海典型饱和软粘土的不排水循环三轴试验，得到塑性应变率和循环次数的双对数线性关系。目前，根据试验数据拟合得到的经验模型已经有很多，因为便于计算，得到了实际工程中的广泛应用。然而，多数经验模型仍存在当循环次数较大时应变拟合不准确的缺陷。

我国烟台港区域的地基中存在大量的软弱土层，地质条件较为复杂，存在沉降和变形等方面的较多技术难题，对港口工程的顺利施工提出了挑战。为此，本文结合烟台港的实际工程，以烟台港的淤泥质粘土为研究对象，进行室内动三轴试验，以围压、静偏应力、动应力、循环次数等为变量，探讨了不同工况下软粘土的累积塑性应变发展规律，并提出一个能合理反映以上各因素影响的经验拟合模型，然后应用于烟台港实际工况，计算结果符合工程实际。

表1 土样物理性质指标Tab.1 Physical properties indexes of soil

1 试验方案

主要进行室内动三轴试验，仪器采用英国GDS动态循环三轴试验仪，土样采用烟台港原状土，土层深度为泥面以下2～5 m，土性为淤泥质粉质粘土，相关物理性质指标如表1所示。

试验土样高度为80 mm，直径为39.1 mm。首先，采用真空抽气饱和法对土样进行饱和，饱和度达到98%以上。然后，依次进行以下试验步骤：

（1）土样在设定的围压σc下进行24 h等向固结。其中，围压σc模拟土体的初始固结压力。

（2）土样固结完成之后，关闭排水阀，先施加静偏应力σj，待土样变形稳定后再施加动应力σd。其中，σj模拟上部结构在地基中引起的附加静应力，σd模拟波浪荷载在地基中引起的动应力。试验施加的循环荷载采用正弦波，周期设为波浪实际周期8 s。为了使土样达到稳定状态，循环周期N设为1 500次。

（3）循环全部结束之后，对土样进行不排水剪切。当总应变达到15%时停止剪切，即得到土样的循环后不排水抗剪强度qd，cu。另外测得未施加循环荷载时土样的不排水抗剪强度qcu=61.804 kPa。然后，可算出循环荷载下土体不排水抗剪强度折减系数，如式（1）所示

单次试验过程见图1，试验方案所含全部工况见表2。其中，定义h=σj/σc为静偏应力比，r=σd/σc为动应力比。

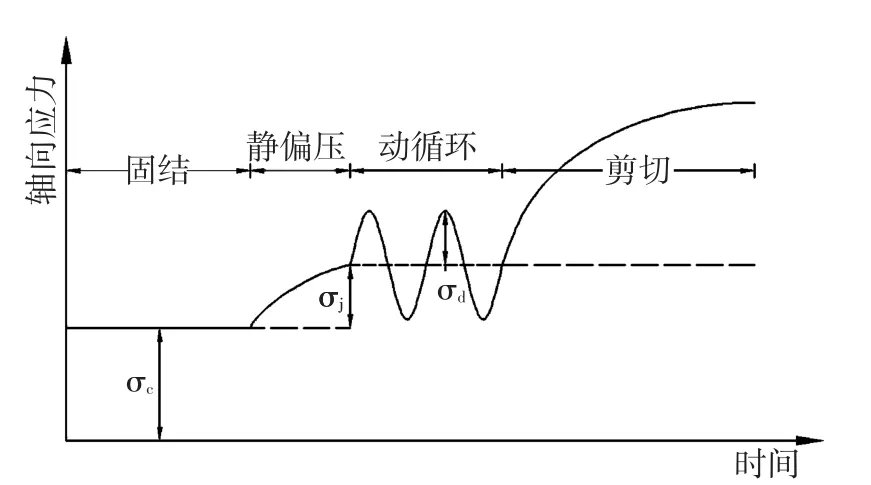
图1 试验加载过程图Fig.1 Loading process diagram of tests

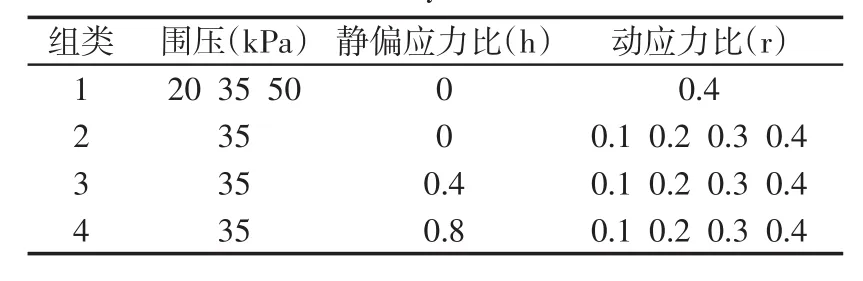
表2 动三轴试验方案Tab.2 Scheme of dynamic triaxial tests

2 试验结果与分析

2.1 循环次数的影响

确定工况下，累积塑性应变随循环次数变化的关系曲线如图2所示（取σc=35 kPa，r=0.4的结果进行分析，各工况下规律相同）。由图可知，随着循环次数的增加，土体的累积塑性应变逐渐增大，且在循环初期增速较快，随后增速放缓，在循环后期趋于平稳。

2.2 围压的影响

静偏应力比、动应力比相同而围压不同的情况下，累积塑性应变的发展曲线如图3所示。由图可知，随着围压值的增大，土体的累积塑性应变逐渐减小，但减小的幅度有限。总体上，当静偏应力比、动应力比一定时，随着循环次数的增加，不同围压下的土体累积塑性应变发展趋势相同，循环后期所达到的稳定值也比较接近。因此，在所研究的土层范围内，可认为不同围压对土体累积塑性应变的发展不产生显著影响。

2.3 静偏应力的影响

动应力比相同而静偏应力比不同的情况下，累积塑性应变的发展曲线如图4所示。由图可知，静偏应力比越大的情况下，土体产生的初始应变值会越大，累积塑性应变的增大速率也越快，循环后期所能达到的稳定值也越大。

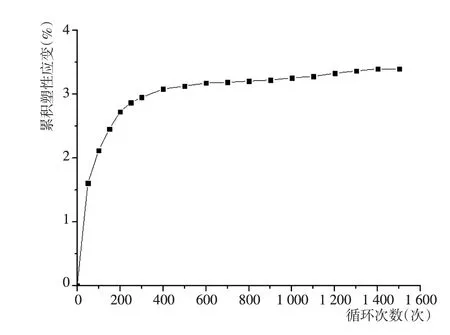
图2 σc=35 kPa，r=0.4，累积塑性应变与循环次数关系曲线Fig.2 Relationship between cumulative plastic strains and cycle times when σcis 35kPa and r is 0.4

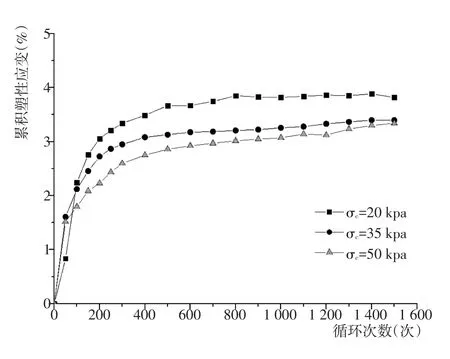
图3 r=0.4，不同围压下累积塑性应变与循环次数关系曲线Fig.3 Relationships between cumulative plastic strains and cycle times with different confining stresses when r is 0.4

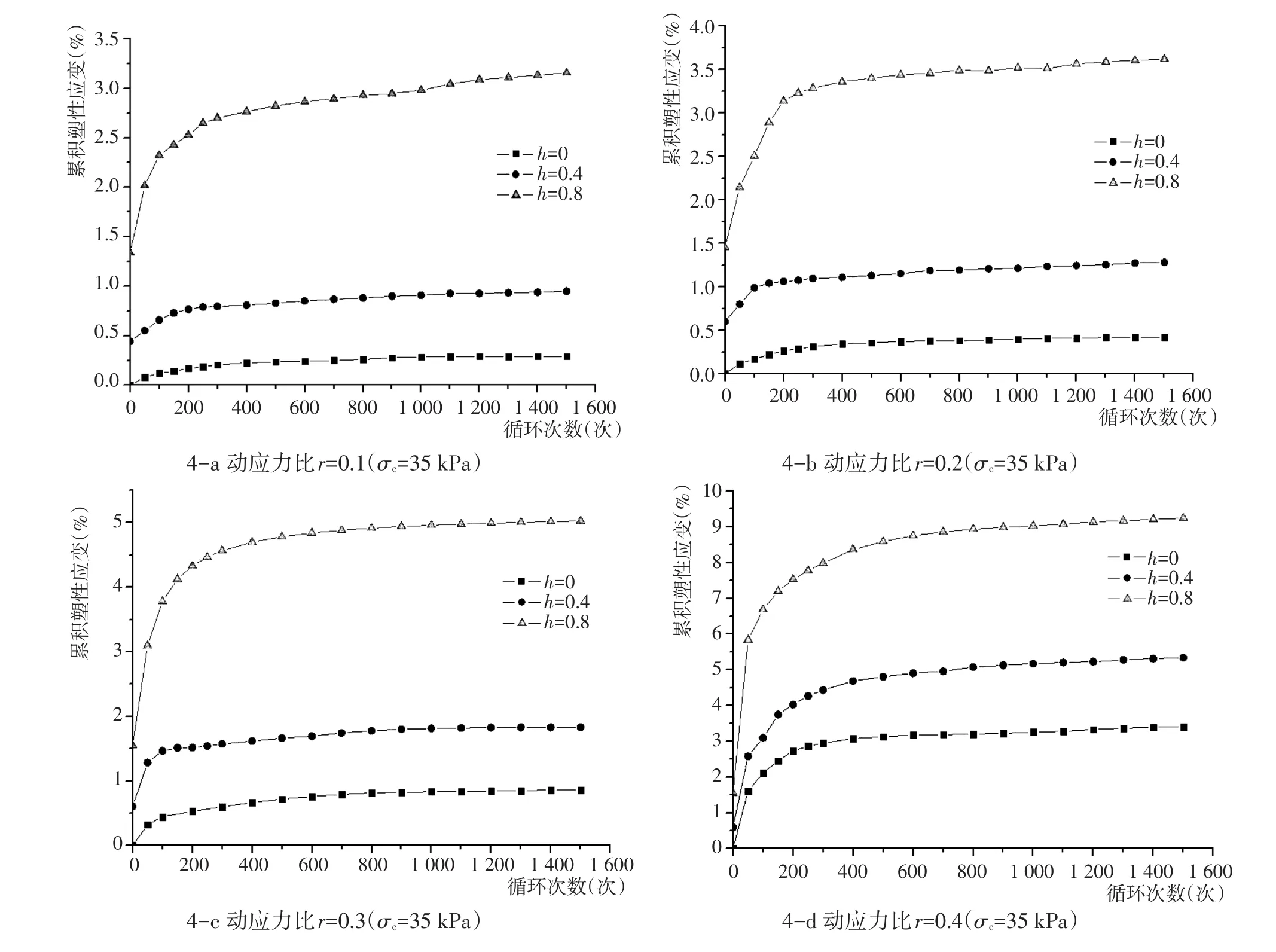
图4 相同动应力比，不同静偏应力比下累积塑性应变与循环次数关系曲线Fig.4 Relationships between cumulative plastic strains and cycle times with different deviator stress ratios

2.4 动应力的影响

静偏应力比相同而动应力比不同的情况下，累积塑性应变的发展曲线如图5所示。由图可知，土体所受的动应力比越大，累积塑性应变的增大速率越快，循环后期所能达到的稳定值也越大。而且，当动应力比达到0.4时，累积塑性应变增幅明显。

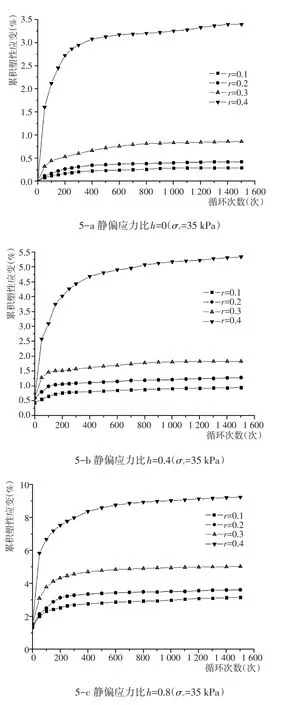
图5 相同静偏应力比，不同动应力比下累积塑性应变与循环次数关系曲线Fig.5 Relationships between cumulative plastic strains and cycle times with different dynamic stress ratios

3 累积塑性应变模型

目前，最常用的累积塑性应变计算方法，多基于Mo⁃nismith等［2］提出的指数模型，如式（2）所示

式中：εp为土体累积塑性应变；N是动荷载循环次数；a、b是试验拟合参数，与动应力水平和土体性质有关。

由式（2）可知，采用Monismith的指数模型计算累积塑性应变时，当循环次数趋于无穷，应变的计算值也会趋于无穷，而实际上应变值应该趋于某一定值。所以，当循环次数较大时，指数模型的拟合并不准确。另外，在Monismith的指数模型中，并未考虑上部结构所传递的初始静偏应力的影响。

为此，本文提出累积塑性应变随循环次数发展的双曲模型，如式（3）所示。当循环次数趋于无穷大时，累积塑性应变趋于定值，双曲线的这一特性更为符合实际情况。而且，式（3）中综合考虑了围压、初始静偏应力、动应力、循环次数等因素的影响。

式中：ε为土体累积塑性应变；N为动荷载循环次数；a、b、d为试验拟合参数，与围压、初始静偏应力、动应力有关。

采用式（3）对各工况下的累积塑性应变发展曲线进行拟合，可得到各参数拟合值如表3所示。

a值决定循环过程中累积塑性应变的增幅，a值越小，循环过程中应变的增幅越大。对a值的拟合结果进行整理，如图6、图7所示，可知a值随着静偏应力比的增大而减小，同时也随着动应力比的增大而减小，符合静偏应力比和动应力比越大时累积塑性应变的增幅越大的规律。而且，由图可知，a值与静偏应力比、动应力比皆呈线性关系，进而对其进行公式拟合，如式（4）所示。

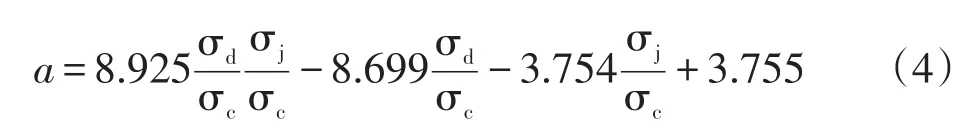
b值决定双曲线的形状，b值越小，曲线的上升速率越快。对b值的拟合结果进行整理，如图8、图9所示，可知b值随着静偏应力比的增大而减小，同时也随着动应力比的增大而减小，符合静偏应力比和动应力比越大时累积塑性应变增大速率越快的规律。而且，由图可知，b值与静偏应力比、动应力比皆呈指数关系，进而对其进行公式拟合，如式（5）所示。

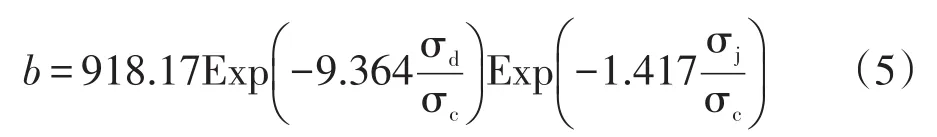
d值是循环前的初始塑性应变，完全由初始静偏应力比决定，与循环过程中施加的动应力比无关。对d值的拟合结果进行整理，如图10所示，可知d值随着静偏应力比的增大而增大，符合初始静偏应力比越大，初始应变越大的规律。而且，由图可知，d值与静偏应力比可用二次函数公式拟合，结果如式（6）所示。

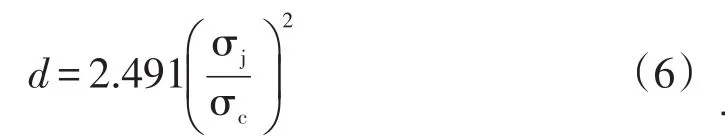
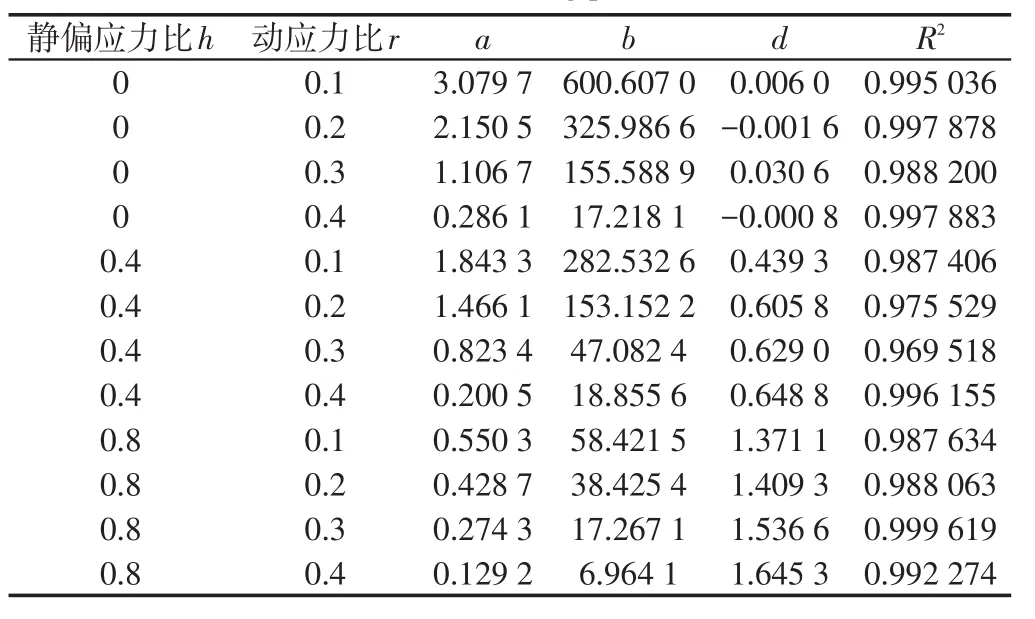
表3 参数拟合结果Tab.3 List of fitting parameters

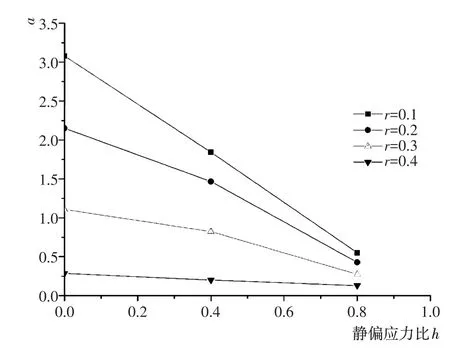
图6 参数a与静偏应力比h的关系Fig.6 Relationships between fitting parameter a and deviator stress ratio h

图7 参数a与动应力比r的关系Fig.7 Relationships between fitting parameter a and dynamic stress ratio r

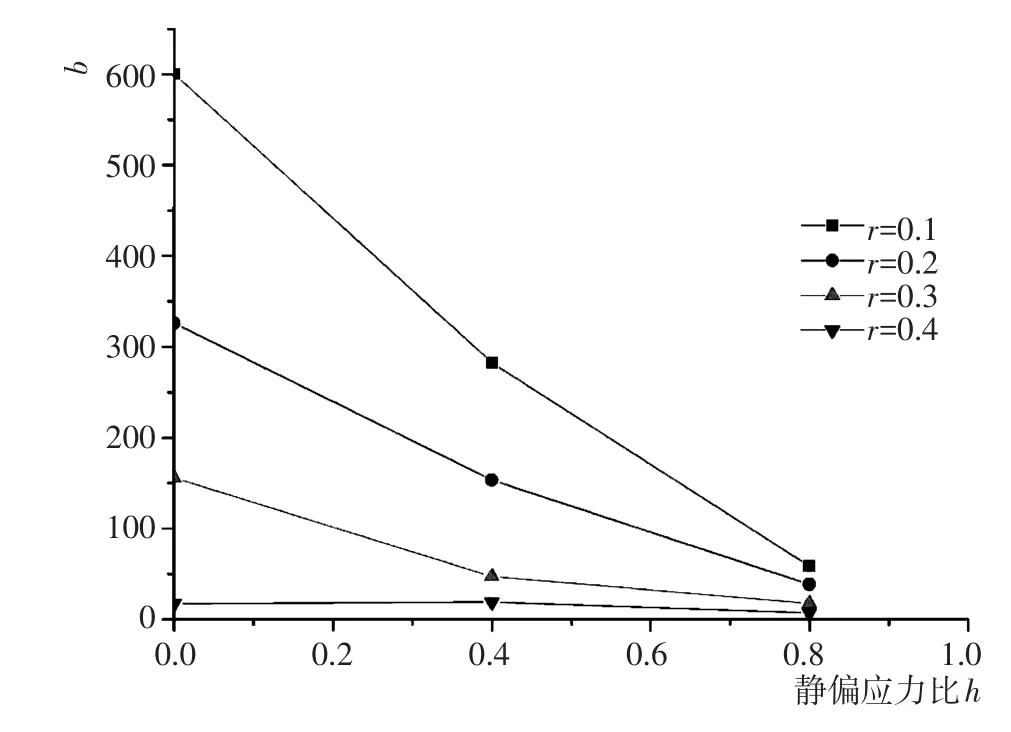
图8 参数b与静偏应力比h的关系Fig.8 Relationships between fitting parameter b and deviator stress ratio h

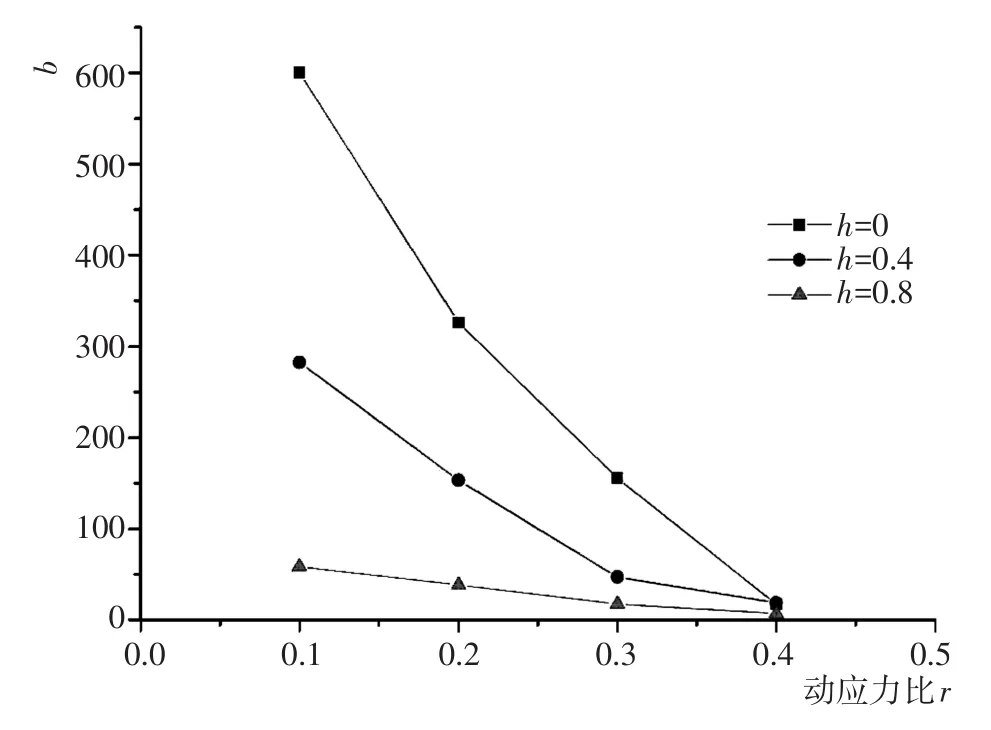
图9 参数b与动应力比r的关系Fig.9 Relationships between fitting parameter b and dynamic stress ratio r

a值和d值共同决定累积塑性应变的最终稳定值。动应力比一定时，静偏应力比越大，导致初始应变越大，应变增幅也越大，最终达到的稳定值就越大；静偏应力比一定时，初始应变是一定的，动应力比越大，导致应变增幅越大，最终达到的稳定值就越大。

将a、b、d的拟合公式代入式（3），即可得到综合考虑围压、静偏应力、动应力以及循环次数的累积塑性应变发展模型，如式（7）所示

利用该双曲模型对各工况进行拟合，并与试验的实测数据进行对比，如图11所示，其中R2=0.94，可知拟合效果良好。

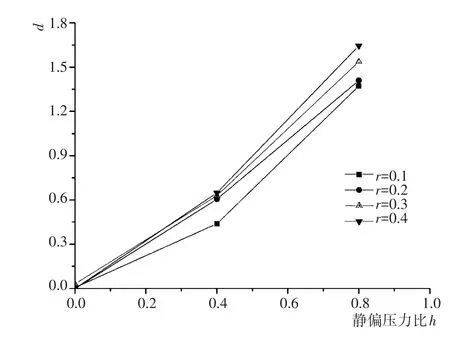
图10 参数d与动应力比r的关系Fig.10 Relationships between fitting parameter d and dynamic stress ratio r

4工程应用

4.1 工程概况

依托烟台港西港区防波堤二期工程，2013年6月开始施工，目前刚完工，即将投入使用。该工程采用的是重力式沉箱防波堤，其典型断面及土层分布情况如图12所示，各土层参数详见表4。计算工况为：设计高水位2.46 m；50 a一遇H1%波浪，波高4.8 m，周期8 s，波浪循环次数取为1 500次。

4.2 计算方法

采用大型通用有限元分析软件ABAQUS建立该防波堤的数值模型。土体计算域在竖直方向取为3倍基床底宽，水平方向则向两侧各取为3倍基床底宽。地基表面设为自由边界，左右皆设为侧限边界，底部设为固定边界。土体本构模型采用Mohr⁃Coulomb模型。地基土体与基床、基床与沉箱底部均设接触面，切向采用库仑摩擦模型并取摩擦系数0.6，法向设为硬接触。模型采用四边形网格、CPE4R单元。

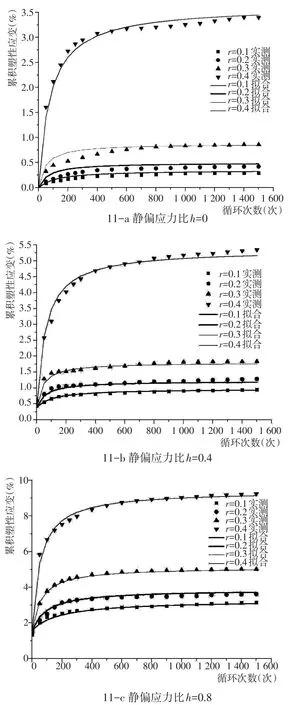
图11 累积塑性应变的拟合曲线与实测数据对比图Fig.11 Fitting curves of cumulative plastic strains versus practical testing curves

通过数值模型计算可得到地基土体中的围压、静偏应力、动应力分布，然后代入式（7）即可得到地基土体中各点的累积塑性应变，最后通过分层法进行累加，即可得到地基的沉降值。

考虑到粉质粘土层、粉土层的土质较好，而且处于地基的最下层，受上部结构及外荷载造成的静偏应力、动应力的影响很小，所以，计算中仅考虑淤泥质粘土层、淤泥质粉质粘土层的累积应变。

图12 防波堤断面及土层分布Fig.12 Section of the breakwater and the soil

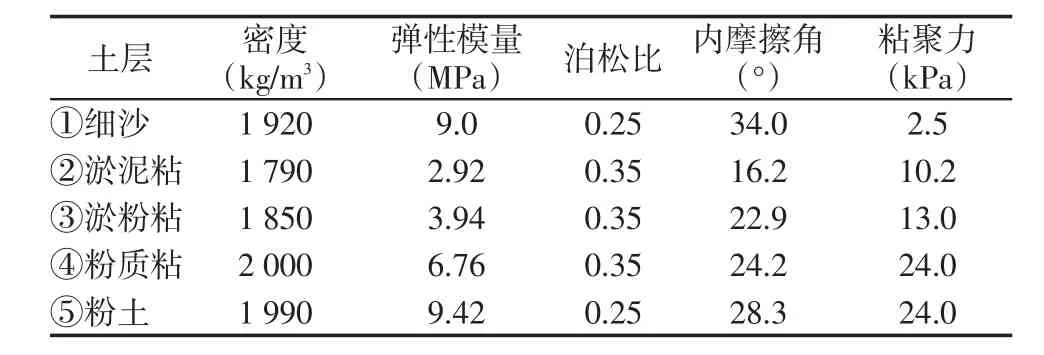
表4 各土层土体物理性质指标Tab.4 Physical properties indexes of soil in different layers

4.3 计算结果分析

通过数值模型计算可得，地基土体中的围压、静偏应力、动应力分布如图13所示。

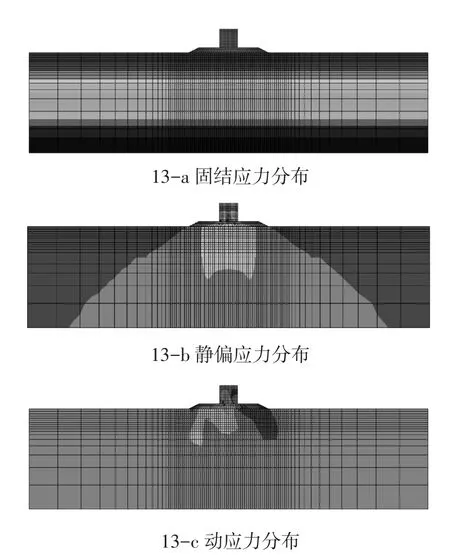
图13 地基土体中的应力分布云图Fig.13 Stresses of the model

以沉箱防波堤的中线以下为计算位置，提取各点的围压、静偏应力、动应力，代入式（7）算得各点的塑性应变值，然后通过分层法计算并累加，可知沉箱沉降值为1.215 m。根据烟台港实测数据，该沉箱断面的最大沉降在1.1 m左右，所以该累积塑性应变发展模型的计算结果符合工程实际。

5 结论

本文以烟台港淤泥质粘土为研究对象，开展动三轴试验，探讨了循环荷载下滨海软粘土的累积塑性应变发展规律，得到以下结论：

（1）在不同围压、静偏应力、动应力的综合作用下，随着循环次数的增加，土体的累积塑性应变都逐渐增大，且在循环初期增速较快，随后增速放缓，在循环后期趋于平稳；

（2）不同围压对土体累积塑性应变的发展不产生显著影响；

（3）静偏应力比越大，土体产生的初始应变值会越大，累积塑性应变增大速率也越快，循环后期所能达到的稳定值也越大；

（4）动应力比越大，累积塑性应变的增大速率越快，循环后期所能达到的稳定值也越大，而且当动应力比达到0.4时，累积塑性应变增幅明显；

（5）综合考虑围压、静偏应力、动应力、循环次数等因素的影响，提出合理描述累积塑性应变发展规律的双曲模型，并根据试验数据对模型参数进行了分析和拟合，拟合结果良好；

（6）在烟台港防波堤的实际工程中应用该累积塑性应变模型，计算结果符合工程实际。

［1］封晓伟.波浪循环荷载作用下防波堤—地基稳定性研究［D］.天津：天津大学，2009.

［2］Monismith C L，Ogawa N，Freeme C R.Permanent deformation characteristics of subgrade soils due to repeated loading［J］.Trans⁃port Research Record，1975，537：1-17.

［3］Chai J C，Miura N.Traffic-load-induced permanent deformation of road on soft subsoil［J］.Journal of Geotechnical and Geoenviron⁃mental Engineering，2002，128（11）：907-916.

［4］Hyodo M，Yasuhara K，Hirao K.Prediction of clay behaviour in undrained and partially drained cyclic triaxial tests［J］.Soils and Foundations，1992，32（4）：117-127.

［5］闫澎旺.往复荷载作用下重塑软黏土的变形特性［J］.岩土工程学报，1991，13（1）：48-53. YAN S W.The deformation behavior of remolded soft clay under cyclic loading［J］.Chinese Journal of Geotechnical Engineering，1991，13（1）：48-53.

［6］王建华，要明伦.软黏土不排水循环特性的弹塑性模拟［J］.岩土工程学报，1996，18（3）：11-18. WANG J H，YAO M L.Elastoplastic simulation of the cyclic undrained behaviour of soft clays［J］.Chinese Jounal of Geotechnical Engineering，1996，18（3）：11-18.

［7］王军.单、双向激振循环荷载作用下饱和软粘土动力特性研究［D］.杭州：浙江大学，2007.

［8］王常晶，陈云敏.交通荷载引起的静偏应力对饱和软黏土不排水循环性状影响的试验研究［J］.岩土工程学报，2007，29 （11）：1 742-1 747. WANG C J，CHEN Y M.Study on effect of traffic loading induced static deviator stress on undrained cyclic properties of saturated soft clay［J］.Chinese Journal of Geotechnical Engineering，2007，29（11）：1 742－1 747.

［9］黄茂松，李进军，李兴照.饱和软黏土的不排水循环累积变形特性［J］.岩土工程学报，2006，28（7）：891-895. HUANG M S，LI J J，LI X Z.Cumulative deformation behaviour of soft clay in cyclic undrained tests［J］.Chinese Journal of Geo⁃technical Engineering，2006，28（7）：891-895.

Experimental research on cumulative plastic strain of littoral soft clay under cyclic loading

WANG Yuan⁃zhan1,HU Shen⁃rong1,YANG Pan⁃bo2
（1.National Key Laboratory of Water Conservancy Engineering Simulation and Security,Collaborative Innovation Center for Advanced Ship and Deep⁃Sea Exploration,Tianjin University,Tianjin 300072,China；2.CCCC First Harbor Consultants Co.,Ltd.,Tianjin 300222,China）

Under the cyclic loading such as waves,the excessive settlement and deformation of soft clay affects the stability of the upper structure.Cyclic triaxial tests on muddy clay from Yantai Port were performed,and then the cumulative plastic strain variation of littoral soft clay under multiple factors,such as confining pressures,devia⁃tor stresses,dynamic stresses and cycle times,have been studied.It has been found that the cumulative plastic strain increases with the increase of cycle times,and it′s fast at the beginning,then slows down,finally achieves sta⁃bility.The cumulative plastic strain is not influenced by the confining pressures obviously,but with a larger deviator stress ratio and a larger dynamic stress ratio,its initial growth is larger,and its final stable value is larger.Accord⁃ing to the test results,a hyperbolic model of the cumulative plastic strain under multiple factors,such as confining pressures,deviator stresses,dynamic stresses and cycle times,has been put forward.Then the model was applied in⁃to Yantai Port engineering,and the results consisted with the engineering.

soft clay;cyclic loading;cumulative plastic strain

TU 411

A

1005-8443（2016）03-0298-08

2015-10-13；

2015-11-19

国家自然科学基金（51279128）；国家自然科学基金创新研究群体科学基金（51321065）；交通运输部交通建设科技项目（2013328224070）

王元战（1958-），男，天津市人，教授，博导，主要从事港口海岸与近海结构设计理论和方法、土与结构相互作用、结构振动分析理论和方法等方面的研究工作。

Biography：WANG Yuan⁃zhan（1958-），male，professor.