低信噪比环境下改进的语音端点检测算法

董 胡

(长沙师范学院 电子与信息工程系，湖南 长沙 410100)

低信噪比环境下改进的语音端点检测算法

董 胡

(长沙师范学院 电子与信息工程系，湖南 长沙 410100)

端点检测在语音识别中具有非常重要的作用，其准确性将直接影响语音识别系统的正确率。为了提高低信噪比环境下语音端点检测的正确率，提出了一种基于多窗谱估计的改进谱减法和能量谱熵的端点检测算法。该算法首先利用多窗谱估计改进谱减法对含噪语音进行去噪以提高语音信号信噪比，接着对去噪后的语音信号使用新的能量谱熵算法进行端点检测。仿真实验结果表明，同常见端点检测算法相比较，该算法在低信噪比环境下具有较好的端点检测正确率且有一定的鲁棒性，证明了该算法的有效性。

多窗谱估计；改进谱减法；谱熵；语音增强；端点检测

0 引 言

语音端点检测是信号处理的一个重要方面[1]。特征参数的提取是一些常见的端点检测方法所普遍重视的方面，却往往忽略了之前的语音增强工作，这将会对端点检测的准确度产生影响[2-5]。相对于短时能量特征，文献[6]提出了对数能量特征。它较好地解决了小幅度的辅音和静音混淆问题，更不会出现短时能量中噪声段特征值过大的情况，能较好地区别语音、噪声和静音。然而，在非平稳含噪环境下，能量较难区分语音与背景噪声,而谱熵可克服能量这一缺点[7-8]。但是，在嘈杂噪声和音乐噪声之下，谱熵变得不稳定,而能量却可抑制该不足之处。根据能量的加性性质，语音与噪声的能量之和大于噪声能量。

基于上述考虑，文中提出了多窗谱估计[9-10]改进谱减和能量谱熵相结合的语音端点检测算法。首先，通过多窗谱估计改进谱减法对含噪语音信号进行谱减增强；接着，使用新的能量谱熵算法进行端点检测。仿真结果表明，在低信噪比环境下，文中提出的新算法与文献[11]提出的改进语音端点检测法相比，有更好的端点检测效果及鲁棒性。

1 多窗谱估计

针对同一数据序列，周期图法仅用单个数据窗，而多窗谱用多个正交的数据窗依次求直接谱，接着求平均以得到谱估计，从而能得到较小的估计方差[12]。多窗谱与周期图相比是一种更准确的谱估计方法。

多窗谱定义为：

(1)

式中：L为数据窗个数；Smt为第k个数据窗的谱。

(2)

式中：x(n)为数据序列；N为序列长度；ak(n)为第k个数据窗，满足多个数据窗互相正交。

(3)

数据窗也叫Slepian窗。Riedal和Siderenko提出下面的正弦窗：

(4)

正弦窗产生的局部偏差比Slepian窗更小，但却具有大致一样的频谱集中度。

利用Matlab软件对多窗谱估计函数和周期图跟真实谱的差异进行对比。其中，周期图使用Hamming窗，真实谱采用AR模型来估计。对比实验采用两个正弦信号叠加：

x(n)=cos(2π×50n)+3cos(2π×200n)

(5)

周期图与多窗谱谱估计性能对比见图1。

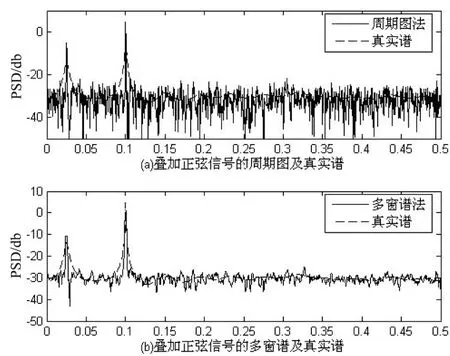
图1 多窗谱与周期图法谱估计性能对比

从图1可知，周期图法的方差性能要劣于多窗谱法。所以，采用多窗谱进行功率谱估计来实现语音增强，能更好地降低音乐噪声。

2 多窗谱估计的改进谱减法

利用Matlab的信号处理工具箱中的多窗谱功率谱估算函数pmtm，可估算多窗谱的功率谱密度，进而获得谱减法中的增益因子，实现谱减语音增强运算[13]。具体步骤如下：

(1)令x(n)为带噪语音，xi(n)为加窗分帧后信号，邻帧之间有重叠。

(6)

以i帧为中心前后各取M帧，共有2M+1帧进行平均。实际中取M为1，即在3帧中进行平均。

(3)对分帧后的信号xi(m)进行多窗谱估计，可得多窗谱功率谱密度P(k,i)(i表示第i帧，k表示第k条谱线):

P(k,i)=PMTM[xi(m)]

(7)

式中，PMTM表示进行多窗谱功率谱密度估计。

(4)对多窗谱功率谱密度估计值也进行相邻帧间平滑处理，计算平滑功率谱密度Py(k,i)：

(8)

以i帧为中心前后各取M帧，共有2M+1帧进行平均。实际中取M为1，即在3帧中进行平均。

(5)已知前导无话段(噪声)占有NIS帧，可以计算出噪声的平均功率谱密度值Pn(k)：

(9)

(6)利用谱减关系。

g(k,i)=

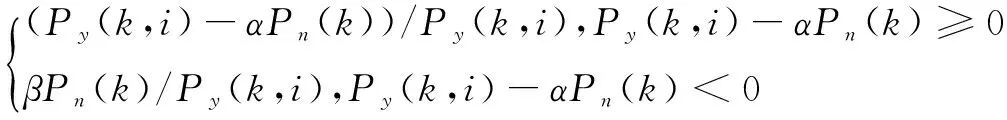
(10)

式中：α为过减因子；β为增益补偿因子。

选择恰当的α值能有效消除音乐噪声，但α值过大则会引起语音失真。

(11)

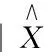
(12)

多窗谱估计的改进谱减算法见图2。

3 对增强后语音信号进行端点检测

3.1 对数能量

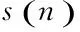
图2 多窗谱估计的改进谱减算法示意图

LE(i) =lg(E(i)+a)-lga

(13)

(14)

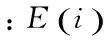
文献[14]实验表明，当a=5×105时，取得了较好的端点检测性能。

3.2 谱 熵

令x(n)为含噪的时域信号，加窗分帧之后得到第i帧信号xi(m)，通过FFT变换，得到第k条谱线频率分量fk的能量谱Yi(k)。定义每个信号频率分量的归一化谱概率密度函数为[15]：

(15)

式中：pi(k)为第i帧中第k个频率分量fk的概率密度；N为FFT长度。

语音帧的谱熵定义为[15]：

(16)

3.3 能量谱熵特征计算

首先，将含噪语音信号通过多窗谱估计的改进谱减法进行降噪处理；接着，对降噪后的信号进行分帧与加窗，再分别计算对数能量与谱熵；最后，将对数能量与谱熵作除法运算，其结果记为B(i)。具体计算表达式定义如下：

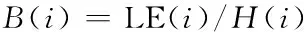
(17)

最终能量谱熵特征计算公式定义如下：

(18)

低信噪比环境下可利用谱熵进行端点检测，而语音信号能量大小的变化则可通过对数能量反映。在无噪声情况下，噪音帧和语音帧的对数能量区别非常明显，因此将两者相除，形成了新的特征参数——能量谱熵。结合两种算法自身一定的抗噪能力，将二者结合起来，在低信噪比环境下的检测能力也有了一定程度的提高，鲁棒性得到增强。

4 仿真实验结果分析

实验语音样本使用TIMIT语音库中450条连续语音,16 kHz采样频率,16 bit量化,单声道wav格式。加噪数据使用NOISEX 92标准噪声库,分别添加white、pink、volvo噪声至纯净语音样本中,分别形成-5dB、0dB、5dB和10dB的含噪语信号1 500条。

含噪语音信号经多窗谱估计改进谱减法增强之后，接着采用能量谱熵法进行端点检测。为了检验文中提出的端点检测算法的效果，分别在white、pink及volvo噪声环境下，将其和文献[11]提出的端点检测法作比较，具体见图3～5。

图3 SNR=-5 dB时white环境下端点检测效果比较

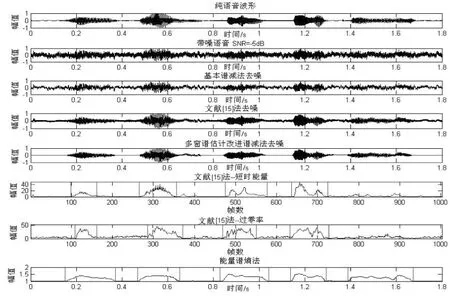
图4 SNR=-5 dB时pink环境下端点检测效果比较

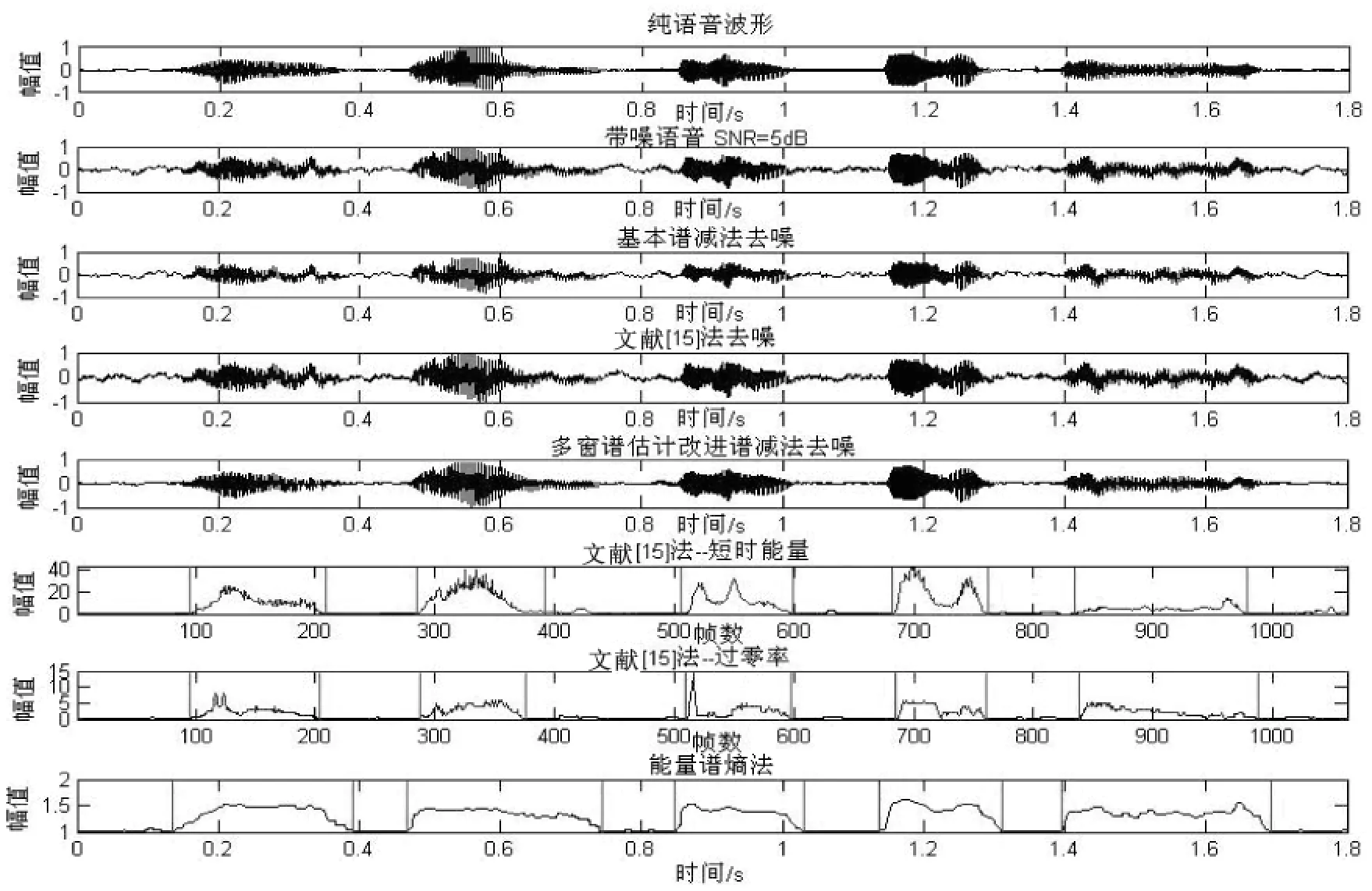
图5 SNR=5 dB时volvo环境下端点检测效果比较

从图3、图5及表1可知，文中提出的能量谱熵算法和文献[11]提出的端点检测算法均可在低信噪比环境下检测出语音的起止端点，但文献[11]提出的端点检测算法的端点检测正确率却低于文中提出的能量谱熵端点检测法。

表1 端点检测正确率比较

从图4可知，文献[11]提出的端点检测算法能检测出语音端点位置但存在漏检，而文中提出的能量谱熵算法却不存在。说明能量谱熵算法有更好的端点检测特性，在低信噪比环境下有更高的端点检测正确率。端点检测正确率定义如下:

错误帧数=语音误判为噪声的帧数+噪声误判为语音的帧数

(19)

正确率=(总帧数-错误帧数)/总帧数

(20)

5 结束语

文中提出了一种低信噪比环境下的语音端点检测算法。该算法通过对含噪语音信号先用多窗谱估计改进谱减法进行增强，提高了语音信号的信噪比，接着采用能量谱熵算法进行端点检测。仿真实验结果表明，该算法在低信噪比环境下能较好地实现语音端点检测，具有良好的抗噪性能，鲁棒性较强，适于实际端点检测应用，从而证明该算法是一种较有效的低信噪比端点检测算法。但是，由于实际背景噪声变化性大，如何进一步改善算法，使其适应更复杂的低信噪比环境将是今后研究工作的重点。

[1] 董 胡.倒谱距离和短时能量的语音端点检测方法研究[J].计算机技术与发展,2014,24(7):77-79.

[2]RabinerLR,SamburMR.Analgorithmfordeterminingtheendpointsofisolatedutterances[J].BellSystemTechnicalJournal,1975,54(2):297-315.

[3] 武 薇,范影乐,庞 全.基于广义维数距离的语音端点检测方法[J].电子与信息学报,2007,29(2):465-468.

[4] 闫润强,朱贻盛.基于信号递归度分析的语音端点检测方法[J].通信学报,2007,28(1):35-39.

[5]JiaChuan,XuBo.Animprovedentropy-basedendpointdetectionalgorithm[C]//ProceedingsofISCSLP.Taiwan,China:[s.n.],2002:96-99.

[6] 肖述才,王作英.端点检测中的一种新的对数能量特征[J].电声技术,2004(6):37-41.

[7]HuangLS,YangCH.Anovelapproachtorobustspeechendpointdetectionincarenvironments[C]//ProcofIEEEinternationalconferenceonacoustics,speechandsignalprocessingproceedings.Istanbul,Turkey:IEEE,2000:1751-1754.

[8] 李荣荣,胡昌奎,余 娟.基于谱熵的语音端点检测算法改进研究[J].武汉理工大学学报,2013,35(7):134-139.

[9] 武鹏鹏,赵 刚,邹 明.基于多窗谱估计的改进谱减法[J].现代电子技术,2008,31(12):150-152.

[10] 彭 军,王 忠,刘兴涛,等.基于多窗谱相关加权语音增强[J].计算机仿真,2011,28(3):142-145.

[11] 鲁远耀,周 妮,肖 珂,等.强噪声环境下改进的语音端点检测算法[J].计算机应用,2014,34(5):1386-1390.

[12]ThomsonDJ.Spectrumestimationandharmonicanalysis[J].ProcofIEEE,1982,70(9):1055-1096.

[13]HuYi,LoizouPC.Incorporatingapsychoacousticalmodelinfrequencydomainspeechenhancement[J].IEEESignalProcessingLetters,2004,11(2):270-273.

[14] 王 民,孙 广,沈利荣,等.基于对数能量倒谱特征的端点检测算法[J].计算机工程与应用,2014,50(16):198-201.

[15]ZhaoH,ZhaoLX,ZhaoK,etal.Voiceactivitydetectionbasedondistanceentropyinnoisyenvironment[C]//Procof5thinternationaljointconferenceonINC,IMS,andIDC.Seoul,Korea:IEEEComputerSociety,2009:1364-1367.

Improved Speech Endpoint Detection under Low SNR Environment

DONG Hu

(Department of Electronic and Information Engineering,Changsha Normal University,Changsha 410100，China)

Endpoint detection has a very important role in speech recognition,its accuracy will directly affect the accuracy of speech recognition system.In order to improve the accuracy of speech endpoint detection under low SNR environment,an endpoint detection algorithm based on spectral subtraction of multitaper spectrum estimation and spectral entropy is proposed.Firstly,it uses improved spectral subtraction of multitaper spectrum estimation to denoise speech signal in order to improve signal to noise ratio,and then it utilizes energy-entropy-ratio algorithm to make endpoint detection for speech signal denoised.Simulation experiment results show that compared with common endpoint detection algorithm,this algorithm has good endpoint detection accuracy and certain robustness in low SNR environment.It proves the effectiveness of the proposed algorithm.

multitaper spectrum estimation;improved spectral subtraction;spectral entropy;speech enhancement;endpoint detection

2015-06-22

2015-09-24

时间：2016-02-18

湖南省科技计划项目(2012FJ3010);湖南省教育科研项目(12C0952);长沙师范学院科研基金项目(XXZD201218);长沙师范学院大学生研究性学习和创新性实验计划项目(DXYC201510)

董 胡(1982-)，男，讲师，硕士，研究方向为信号处理及嵌入式设计。

http://www.cnki.net/kcms/detail/61.1450.TP.20160218.1636.064.html

TN912.35

A

1673-629X(2016)03-0071-04

10.3969/j.issn.1673-629X.2016.03.017