双曲拱桥加固及静动载检测数值模拟研究
2016-02-23王大刚
王大刚
(中国电子工程设计院,北京100142)
双曲拱桥加固及静动载检测数值模拟研究
王大刚
(中国电子工程设计院,北京100142)
针对双曲拱桥损坏现状,提出主拱圈加固采用锚喷技术,并将拱型结构变成箱型结构的加固方案,采用有限元分析方法对加固后双曲拱桥进行了动静力响应分析,并进行静动载试验,将计算结果和现场试验数据进行对比分析。结果表明,静荷载为40t、35t、30t条件下,相关挠度为46%~65.3%、28%~62.4%、52.8%~61.7%;行车速度为22km/h、26km/h和32km/h,相应冲击系数为1.084、1.165和1.181;分析挠度和应变校验系数分布规律可知,本次加固后桥梁整体稳定性和刚度较好,安全度较高;评定加固后的桥梁承载性能,为双曲拱桥维修加固提供了可靠参考。
双曲拱桥;加固;静动载;数值模拟
【DOI】10.13616/j.cnki.gcjsysj.2016.06.029
1 引言
双曲拱桥是我国自行设计建造的一种桥型,已有数十年历史,由于其具有较好的受力性能和承载能力,因此在中小桥中得到广泛采用。双曲拱桥的主要组成部分包括拱波、拱板、拱肋和横向隔板等,由于双曲拱桥具有化整为零的施工特点,因此不需大型施工设备。双曲拱桥具有结构简单、节省建筑材料和具有较大桥下净空等特点,但由于设计建造时间较早,因此存在较多问题,如结构安全系数较低、抗震性能较低和抗疲劳破坏能力较差等,因此在当前繁重交通荷载作用下,出现了不同程度的病害,其中一部分病害较为严重,部分丧失或全部丧失继续承载能力,因此不得不对其进行加固处理。
双曲拱桥的病害主要有上部结构病害和下部结构病害。上部结构病害主要包括:(1)由于建造时期用钢量不足,导致桥梁结构延性较差,造成拱波的纵向开裂;(2)双曲拱桥横隔板厚度和刚度不足,造成桥梁整体稳定性较差,产生较大的应力集中,从而引起拱波裂缝。下部结构病害主要包括:(1)建造时期混凝土强度不足,在长期处于外界条件下发生碳化反应,造成桥梁耐久性不足,以至于钢筋锈蚀,拱脚处裂缝较多;(2)建造时期,由于施工能力有限,造成基础浅埋,基础浅埋会发生地基承载力不足的现象,从而产生不均匀沉降,造成桥梁开裂。
经过多年使用,现役大量双曲拱桥呈现出不同程度的损坏,对交通安全造成较大隐患[1~4]。本文根据实际调查,采用合适的加固方法和施工工艺,进行全桥静、动载作用下桥梁仿真模拟实验,评定加固后的桥梁承载性能,为双曲拱桥维修加固提供可靠参考。
2 主拱圈加固方案
施工技术依据《公路桥涵施工技术规范》[5]规定。针对双曲拱桥主要损坏部位主拱圈,采用锚喷技术进行加固,拟在拱肋底部处施工增设14cm的混凝土板,并将其浇筑成整体,以增加其整体刚度和稳定性,采用箱型结构替换原来拱型结构,调整后的桥梁拱圈截面图如图1所示。

图1 加固后的主拱圈截面(单位:cm)
3 静载试验
3.1 测试截面和工况布置
根据外观普查结合桥梁荷载试验要求,选择第2孔作为荷载试验孔。加载数值分别为30t、35t、40t,加载位置分别为拱脚、1/4跨和跨中。
3.2 静荷载条件下数值计算
为了验证上述加固后桥梁整体稳定性和安全性,对桥梁整体进行数值模拟。在本次数值计算中,钢筋混凝土材料采用SOLID65单元进行模拟,其他部位采用SOUD95单元进行分析,建立三维数值模拟。本次数值模拟共划分81526个三维实体单元和56648个节点,其中钢筋结构单元共18862个。本次数值计算模型网格如图2所示。
3.3 数值模拟结果分析
3.3.1 变形分析
为了验证加固效果和数值模拟的准确性,将不同截面挠度变形的理论值和监测值进行对比分析。
在分别40t、35t、30t静荷载条件下,不同实测断面,不同荷载作用条件下,挠度校验系数值分别在46%~65.3%、28% ~62.4%、52.8%~61.7%之间,满足相关规范要求[5]。不同荷载作用、不同截面条件下,结构部件相对残余应变都较小,符合规范要求,结构处于弹性工作状态,表明加固后拱桥工作性能和整体稳定性都较好。

图2 结构单元离散图
3.3.2 应变分析
在试验荷载作用和有限元软件ANSYS数值模拟情况下,对偏载拱脚截面、偏载1/4截面、偏载拱顶截面中载拱脚截面、中载1/4截面、中载拱顶截面进行应变理论值和实测值的校核。
在40t、35t、30t荷载作用下,各测试截面各工况应变校验系数值分别在29.8%~98.2%、31.8%~101.2%、68.9%~101.9%之间,可以得到不同截面条件下应变校验系数,与相关规范比较可知,满足强制性要求[6]。试验和数值计算表明:相关结构部件的残余应变小于规范规定的20%,表明加固后拱桥工作性能较好。
4 动载现场试验
4.1 自振频率
4.1.1 振型比较
通过ANSYS模拟得到前三阶振型中第一阶振型实测值2.930,计算值为6.107;第二阶振型实测值5.423,计算值为8.181;第三阶振型实测值6.039,计算值为8.820。由上述数据可以看出:第一阶振型数值最小,第三阶振型数值最大;第一阶振型计算值与实际值相差最大,第三阶振型计算值与实际值相差最小,表明对第一阶振型计算时考虑影响因素不足,造成误差较大。
4.1.2 自振频率比较
静动荷载现场试验条件下,得到的拱桥频谱图如图3、图4所示。经傅里叶变换及相关处理可以得到上部结构前三阶频率实测值。结合图3和图4可以看出:在荷载作用前期,振动幅值变化较小;随着时间增长,振动幅值变大,表明振动幅值与时间有关。

图3 跨中实测基频自谱分析

图4 20km/h跑车跨中强迫振动
4.2 强迫振动
4.2.1 强迫振动时程曲线

图5 30km/h跑车跨中强迫振动
4.2.2 冲击系数
对加固后拱桥进行了动荷载条件下现场试验,得到了预定断面的动挠度,将其与静荷载作用下挠度对比分析可知:行车速度为22 km/h:相应冲击系数为1.084;行车速度为26km/h:相应冲击系数为1.165;行车速度为32km/h:相应冲击系数为1.181;较理论值偏小。上述结果表明:数值计算简化了模型复杂程度,因此,计算得到的自振频率小于实测结果,且冲击系数也小于实测结果,这表明结构动力性能良好。
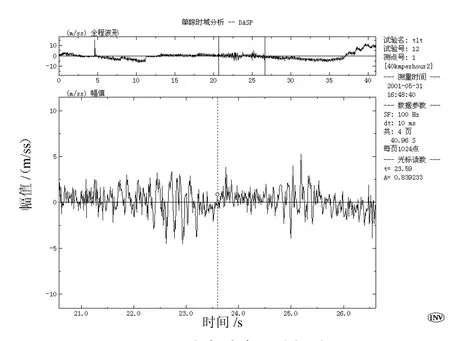
图6 40km/h跑车跨中强迫振动
5 结论
1)采用有限元软件ANSYS对加固后拱桥进行了动静力响应分析,得到了材料非线性条件下加固后拱桥自振频率、振形等数据,并将计算结果和现场试验数据进行对比分析,结果表明数值模拟可以较好模拟拱桥结构受力特性;
2)由静动荷载试验数据,分析拱桥上部结构挠度变化规律和应变校验系数分布规律可知,本次加固后桥梁整体稳定性和刚度较好,安全度较高;
3)数值计算简化了模型复杂程度,因此计算得到的自振频率小于实测结果,且冲击系数也小于实测结果,这表明结构动力性能良好。
【1】GB 50086—2001锚杆喷射混凝土支护技术规范[S].
【2】王国鼎,钟圣斌.拱桥(第二版)[M].北京:人民交通出版社,2000.
【3】朱宏军,程海丽,姜德民.特种混凝土和新型混凝土[M].北京:化学工业出版社,2004.
【4】张劲泉,魏洪昌,徐岳等.公路旧桥加固成套技术及工程实例[M].北京:人民交通出版社,2007.
【5】JTG/TF 50—2011公路桥涵施工技术规范[S].
【6】交通部.公路旧桥承载能力鉴定方法(试行)[Z].1988
Study on Reinforcement and Satic-dynamic Load Test of Double Curved Arch Bridge
WANG Da-gang
(ChinaElectronicsEngineeringDesignInstitute,Beijing 100142,China)
Aimingatthedamagestatusofdoublecurvedarchbridge,themainarchreinforcedbyshotcretetechnology,thereinforcement schemeofthearchstructureintoboxstructure,finiteelement analysismethodisusedto analyzethedynamicresponseofthe double curved archbridge.Staticanddynamicloadtestswerecarriedoutonthebridge,thecalculationresultsandfieldtestdatawerecomparedandanalyzed. The results show that:The static load is 40t,35t,30t conditions,the relevant deflection is 46%~65.3%,28%~62.4%,52.8%~61.7%.The drivingspeedis22km/h,26km/hand32km/h,thecorrespondingimpactcoefficientwas1.084,1.165and1.181.Analysisofdeflectionand straindistributionofthecalibrationcoefficient,theoverallstabilityofthebridgereinforcementandgoodstiffness,ahighdegreeofsafety;the performance evaluation ofbridge bearingafterreinforcement,to providea reliable reference forthe maintenance of hyperbolic arch bridge reinforcement.
double-curved arch bridge;reinforce;staticanddynamicload;numerical simulation
U445.7+2;TU441+.2
A
1007-9467(2016)06-0111-03
2016-04-15
王大刚(1977~),男,黑龙江集贤人,高级工程师,从事建筑工程设计与研究,(电子信箱)44295743@qq.com。
