基于ANNF和结构相似性的单帧超分辨率图像重建算法

徐燕华，李荣，王华君，徐平平

基于ANNF和结构相似性的单帧超分辨率图像重建算法

徐燕华，李荣，王华君，徐平平

针对相似最近邻算法ANNF较差的稳定性，提出了一种字典学习和简单正则化相结合的算法，在ANNF处理之后，运用结构相似性对其进行简单正则化操作。首先解决单一图像的SR字典学习问题；然后利用k-d树对输入的图像特征匹配进行运算，得到ANNF映射；最后将ANNF结果进行相似性正则化处理，只需要几次迭代就能完成后续处理，得到最终的高分辨率图像。采用峰值信噪比PSNR和均方误差RMSE比较各算法效果。从实验结果数据可以看出，算法具有最高的PSNR值和最低的均方误差，从实验结果图像可以看出，其算法的纹理保留的最好，效果最自然，另外从对高斯模糊的鲁棒性分析来看，算法鲁棒性完全优于其他算法。

相似最近邻；正则化；k-d树；结构相似性；鲁棒性

0 引言

超分辨率（super-resolution，SR）[1]是通过软件算法的方法来提高图像的分辨率，从而给用户更多的图像细节，SR也是机器视觉领域非常热门的研究课题。在军事、地球卫星、医学图像领域都有涉及[2,3]。由于硬件设备上提高分辨率已经基本到了极限，从软件上获得高分辨率（High Resolution，HR）图像比较实际可行[4]，然而，至今商业用途的SR非常少，主要是由于获得实际需要的低分辨率（low resolution，LR）图像比较难，用于学习的数据库并不完善。

一般SR算法一般分为三大类：基于插值的算法，基于学习的算法和基于正则化重建的算法。基于插值算法的主要优点是简单直接，但插值结果可能会模糊一些尖锐的纹理细节，如文献[5]提出了一种改进的插值算法，添加了更多的先验知识，如平滑先验和噪声先验，但结果依然有振铃和模糊等效果。

基于正则化重建的SR算法经常需要多帧信息以提供更多的额外信息，用正则化对这些信息进行约束。如文献[6]提出了一种利用自身实例图像的SR问题，用高斯先验和L2正则化进行鲁棒估计，然而，对异常点（outlier）处理依然比较乏力。文献[7]提出了基于实例图像回归的快速SR算法，即In-Place Example Regression，简称IPER，所使用的图像块数据库不需要大量的实例学习，拥有比较快的运行速度，效果不错，然而，该算法对先验知识的依赖性比较强，而且输入图像不能有任何其他模糊，如运动模糊。

基于学习的SR算法近几年才兴起，主要是基于稀疏表达，将信号的稀疏表达运用到HR图像的线性表示，在压缩传感中应用较多。文献[8]提出了基于多尺度结构自相似性的单幅图像超分辨率算法，充分利用结构自相似性在多尺度上的应用，该算法不需要较大的数据库，然而，在字典数据的构建上并不完善。

文献[9]提出了广义相似最近邻域（Approximate Nearest Neighbor Field, ANNF），即源图像块与目标图像块周围区域也匹配，并将其运用到SR算法中，其优势是速度快，但表现得并不稳定，因为自然图像的复杂性并不总是满足ANNF。

本文给出一种新的单帧图像SR算法，在文献[9]的基础上，使用相似最近邻算法ANNF结合结构相似性进行单帧超分辨率，其中ANNF用于单帧SR的字典学习和初步重建，结构相似性正则化提供自然图像结构相似的先验知识和稳定的估计，实验结果表明本文算法具有更好的稳定性和效果，是ANNF的有效改进。

1 学习阶段

为了求解目标图像与源图像的ANNF映射关系，令每个p×p的图像块的特征匹配（Feature Match, FM）计算如下：

平均颜色值；

x，y方向的梯度平均值；

图像块的最大值。

选用以上这些特征，作为k-d树[10]的输入，FM计算目标图像到源图像最近邻的每个图像块。根据初步ANNF的映射，FM利用图像间“相关性”属性来提高ANNF映射。图像之间的“相关性”体现在区域的相关性[11]。即如果目标图像在(xtar,ytar)处图像块与源图像块在(xorg,yorg)处的图像块匹配，则它们各自的邻域也能相互匹配。

为了重建最终的HR图像，需要使用一般源图像的高分辨率形式SHR，即如果(x,y)=ANNFmap(i,j)，使用SHR的p×p的图像块去重建最终输出的高分辨率图像OHR。由于采样的密集性，对DHR的每个位置(i,j)中p×p个值与输出图像(i,j)处的值相关联，这些重叠图像块的均值可用于去除异常值，获输出图像OHR在该处的像素值。例如，为了获得像素值OHR(i,j)，需要获取所有映射到该点处的图像块，经验上去除最大和最小的异常值，其他值取平均。学习阶段的算法如算法1所示：

?

值，其他值取平均。End

2 超分辨率重建

虽然ANNF计算起来比较简单，效果也可以接受，但稳定性并不好，为此，利用一些先验知识对其进行简单正则化增强其稳定性。众所周知自然图像都拥有大量的自相似小图像块，这是局部图像结构在不同尺度下的重现[8-12]，例如在某个自然图像上取一个8×8的小图像块，一定能在这幅图像上找到和这一图像块最匹配的图像块。引入图像块相似性作为图像重建的新的先验知识，其能量函数如式（1）：

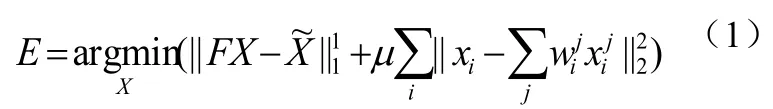
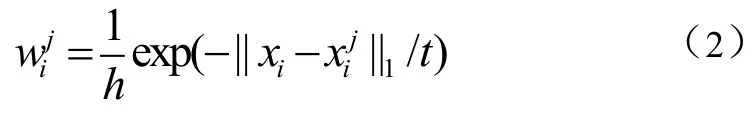
式（2）中，h是归一化因子，t是控制相似度的标量。式（2）可以简化为式（3）：

式（3）中，I是单位矩阵，A是N×N的矩阵，N是原始超分辨率图像维数。矩阵A中元素满足[14]式（4）：

这里迭代可以采用简单的最速下降法，迭代公式如式（5）：

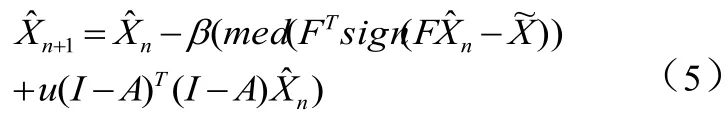
式（5）中，med为中值函数，中值函数在SR数值运算中具有非常好的鲁棒性和稳定性[15]。迭代直至满足前一次迭代值和当前值的绝对值差在给定阈值内，公式表示如式（6）：

式（6）中，α值为预设的阈值。

提出的重建算法可以简要描述为算法2。

算法2：输入：初始低分辨率图像S L R，缩放因子s，阈值α，t，T，β，μ，变换算子F；输出: 输入图像的S R形式，O H R；

SHR是一般源图像的高分辨率形式；DLR=upscale（downscale（SHR，s），s）；IPbic=upscale（IPbic，s）；upscale和downscale是采用立方插值的放大和缩小的函数k-d树计算；ANNFmap=；W，H分别是IPbic的宽高。For 0＜ i ＜W, 0 ＜ j ＜H For i-p/2 ＜ k＜ i+p/2, j-p/2 ＜ l ＜ j+p/2FM{DLR} IPbic,x=ANNFmap(k);y=ANNF ,lmap(k);,l v=SHR[x+i -,y+j-]; kl End去除v的异常值，即在p×p的图像块范围内去除最大最小值，其他值取平均。End设置迭代次数loopnum = 4；If 迭代次数未达到loopnum且不满足式（6）的条件将OHR作为Xˆ代入式（5），n Xˆ1FsignX-X)) =ˆ-Xβ(med(T～n+n(Fˆn+(I u-)I-)X) A(TAˆnOtherwise End loop

4 实验结果与分析

仿真实验在配置为Windows XP操作系统、intel酷睿II双核处理器、1.86 GHz主频、4 GB RAM的笔记本计算机进行。实验平台是MATLAB 7.0。

4.1 参数设置及评价标准

选择的图像块尺寸为a= 5，迭代缩放因子为r= 2。输入的LR图像X0立方插值生成目标HR图像X，阈值α取0.6，μ取1，β取1，代表相似度的阈值T取4，控制相似度的标量t取8。

使用图像的峰值信噪比（Peak Signal to Noise Ratio, PSNR）和均方根误差（root-mean-square error, RSME）表征估计得到HR图像的好坏。

4.2 实验结果比较

实验所用图像大多采自文献[6][7]，用于比较测量的图像如图1所示：

图1 用于SR效果比较的图像

用于对比的算法是文献[9]提出的ANNF算法，文献[8]提出的IPER算法和文献[6]提出基于局部实例图像上采样算法，ULSE。

为了获得客观的评估结果，首先使用均方误差RMSE和峰值信噪比PSNR评估结果，如表1所示：

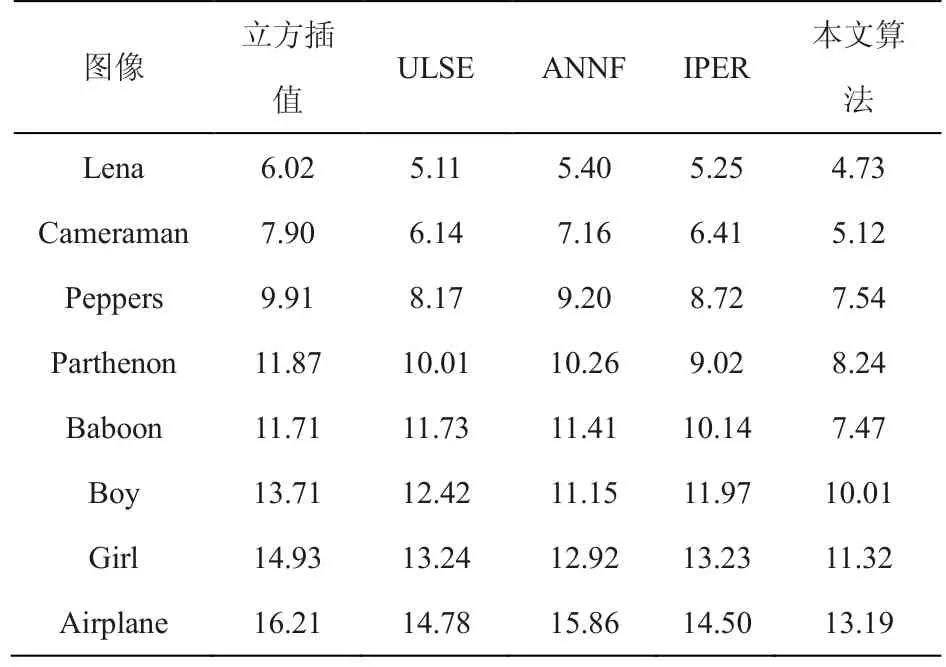
表1 分辨率增强因子为2时各算法RMSE结果

从表1可以看出立方插值的结果最差，因为立方插值假设图像是平滑先验的。IPER的效果明显好于立方插值，RMSE明显低于立方插值的RMSE值。ANNF和MSS的结果差不多，RMSE的值相差不大。本文算法拥有最低的RMSE，这是由于本文算法在ANNF之后，对其进行简单的结构相似性正则化的结果。

表2是PSNR的值测量结果，PSNR值越高表示图像的高频成分丢失得越少，从表2可以看出本文算法的PSNR值最高，与原始图像的PSNR值相差不多，丢失的高频纹理信息最少。

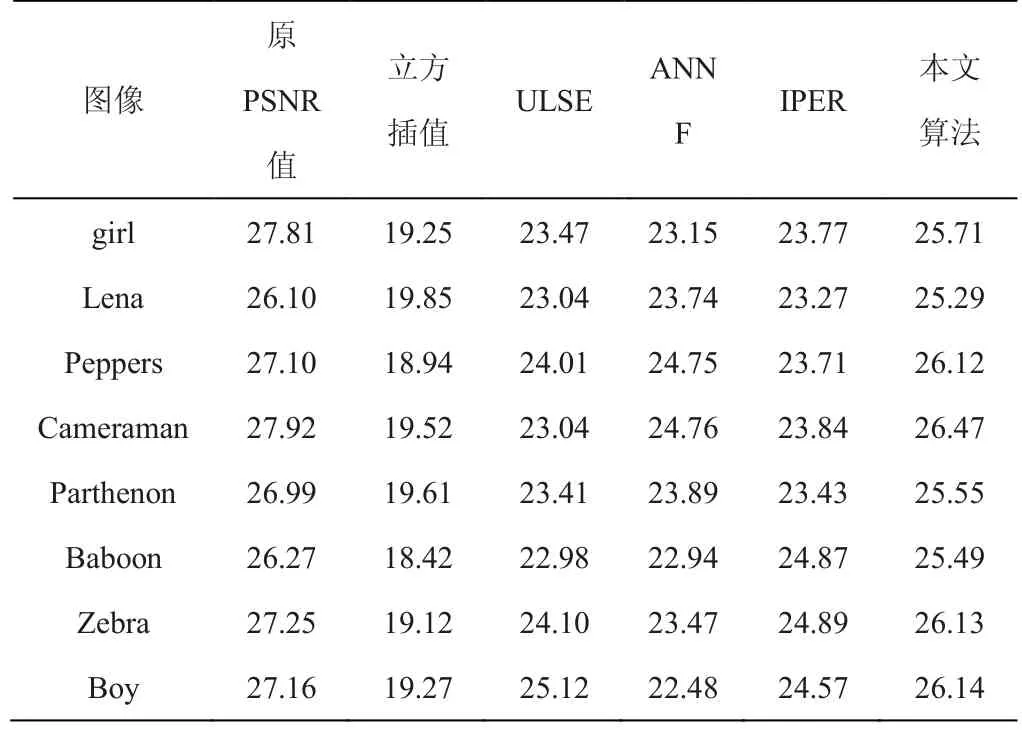
表2 分辨率增强因子为3时各算结果的PSNR值（/dB）

4.3 输出图像比较

不同算法在Parthenon上的结果如图2所示：

图2 第一层左起原始图像、立方插值图像、ULSE，第二层左起ANNF、IPER和提出的算法（4倍）

从图中可以看出，ULSE和IPER算法获得了很多尖锐效果，会引起视觉上的不舒服，在眼睛周围有鬼影和振铃效应，提出的算法获得的重建效果更佳自然，体现了ANNF算法结合结构相似性正则化后的优势。

4.4 对高斯模糊的鲁棒性

讨论前提是输入图像没有模糊，若有较大的运动模糊，字典匹配将无法进行。因此本文这里讨论常见的高斯模糊，用3×3或者5×5等高斯核卷积模拟高斯模糊，然后进行SR操作。

高斯卷积核的大小与PSNR的关系如图3所示：

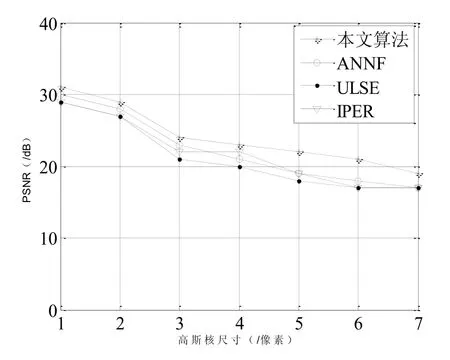
图3 高斯核尺寸与PSNR关系

可以看出随着卷积核的逐渐变大，提出算法的PSNR值下降最慢，高斯卷积核大小与RMSE关系图如图4所示：

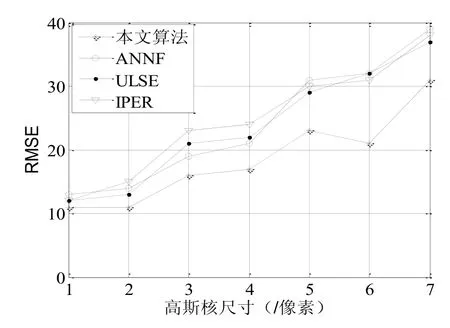
图4 高斯核尺寸与RMSE关系

可以看出本文算法的RMSE值上升最慢。所以本文算法对于高斯模糊是具有一定鲁棒性的，优于其他算法对高斯模糊的鲁棒性。也可以看出，在ANNF算法后应用结构相似性正则化的必要性，可以很好提高其稳定性。

5 总结

在ANNF算法的基础上，将结构相似性巧妙结合在一起，ANNF算法结束后进行相似性正则化，充分运用了自然图像的相似性属性，使ANNF算法更加稳定有效。仿真实验表明本文算法结果更接近真实HR图像，纹理更加清晰自然，而且对一些高斯模糊具有一定鲁棒性。

未来将重点研究带有模糊的字典学习方法用于处理低分辨率同时有一定运动模糊SR问题，扩大算法适用性，而不仅仅是压缩传感层面的。

[1] 苏衡, 周杰, 张志浩. 超分辨率图像重建方法综述[J].自动化学报, 2013, 39(8): 1202-1213.

[2] 杨文波. 航空图像超分辨率重构技术研究[D]. 长春:中国科学院研究生院长春光学精密机械与物理研究所, 2014.

[3] 曾蕾. 图像稀疏表示及图像超分辨应用研究[D]. 电子科技大学, 2014.

[4] 江毅, 黄俊斌. 基于波分复用器的光纤光栅振动传感器阵列[J]. 中国激光, 2005, 32(11):1525-1528.

[5] S Mallat. and G.Yu, Super-resolution with sparse mixing Estimators[J]. IEEE Trans on Image Processing, 2009, 19(11):2889 - 2900.

[6] Freedman G, Fattal R. Image and video upscaling from local self-examples.[J]. ACM Transactions on Graphics, 2011, 30(2):474-484.

[7] Yang J, Lin Z, Cohen S. Fast image super-resolution based on in-place example regression[J]. ieee conference on Computer Vision & Pattern Recognition, 2013, 9(4):1059-1066.

[8] 潘宗序, 禹晶, 胡少兴,等. 基于多尺度结构自相似性的单幅图像超分辨率算法[J]. 自动化学报, 2014, 40(4): 594-603.

[9] Ramakanth S A, Babu R V. Featurey match: A general ANNF estimation technique and its applications.[J]. IEEE Transactions on Image Processing, 2014, 23(5):2193-220 5.

[10] 钱银玲, 梁晓, 张严辞. 基于Bin的高质量k-D树构建算法[C]// 第九届中国计算机图形学大会. 2012, 24(7): 984-989.

[11] 浦剑, 张军平. 基于词典学习和稀疏表示的超分辨率方法[J]. 模式识别与人工智能, 2010, 23(3): 335-340.

[12] 吴炜, 郑成林, 张莹莹等. 广义非局部均值和自相似性的超分辨率算法[J]. 西安电子科技大学学报, 2014, 27(4):100-107.

[13] 张曼, 沈旭昆. 一种基于尺度空间的三维点云数据配准算法[J]. 系统仿真学报, 2009, 24(9):131-135.

[14] 兰诚栋, 陈亮, 卢涛. 利用位置权重稀疏表示的人脸超分辨率算法[J]. 武汉大学学报：信息科学版, 2013, 38(1):27-30.

[15] Farsiu S, Robinson D, Elad M, et al. Fast and robust multi-frame super-resolution[J]. IEEE Transactions on Image Processing, 2003, 13(10): 1327-1344.

A Single Frame Super Resolution Algorithm Based on ANNF and Structural Similarity

Xu Yanhua1, Li Rong1, Wang Huajun1, Xu Pingping2
(1. Taihu University of Wuxi, Wuxi 214064, China; 2. School of Information Science and Engineering, Southeast University, Nanjing 211189, China)

For the issue of the poor stability of the algorithm of approximate nearest neighbor field ANNF, a new algorithm based on dictionary learning and simple regularization is proposed. After ANNF process, simple structural similarity regularization operation is applied. Firstly, single image dictionary learning must be solved. Then k-dimensional tree is used to deal with the input feature matching, giving ANNF mapping. Finally results from ANNF are regularized by similarity process. The process only needs a few iterations with following up a final high resolution image. In this paper, PSNR and MSE are used to compare the results of the algorithms. The data results show that the proposed algorithm has the highest PSNR value, and the lowest RMSE value. The experimental image results show that the image’s texture can be reserved best, the nature of the images is best. In addition, from the robustness analysis of gauss blur, the robustness of the proposed algorithm is much better than other algorithms.

Approximate nearest neighbor field; Regularization; k-dimensional tree; Structural similarity; Robustness

TP391

A

1007-757X(2016)10-0026-04

2016.01.05）

江苏省高校自然科学研究项目（No.14KJD460004）

徐燕华（1979-），女，无锡人，无锡太湖学院，讲师，硕士，研究方向：图像处理、智能算法等，无锡 214064

李 荣（1978-），女，淮安人，无锡太湖学院，讲师，硕士，研究领域：目标跟踪、图像处理等，无锡 214064

王华君（1979-），男，宜兴人，无锡太湖学院，讲师，硕士，研究领域：图像处理、图像重建等，无锡 214064

徐平平（1957-），女，南京人，东南大学，信息科学与工程学院，教授，博导，博士，研究领域：图像处理、目标跟踪等，南京 211189