基于SVG控制应用的数字滤波器实用设计

方存洋， 施胜丹

(国电南瑞科技股份有限公司，江苏 南京 211106)

基于SVG控制应用的数字滤波器实用设计

方存洋， 施胜丹

(国电南瑞科技股份有限公司，江苏 南京 211106)

IIR型数字滤波器凭借其优良的衰减特性在利用软件处理信号的场合应用广泛。针对无功发生器(svg)控制保护装置应用程序开发过程中所使用的IIR数字滤波器，利用MATLAB中的FDAtool工具获得阶数和传递函数系数，并通过微调零极点位置获得较为理想的幅频曲线，并输出系数写入控制程序的函数中；分析采样周期对滤波器零极点位置的影响，在不同采样周期下，数字滤波器零极点位置发生改变，产生新的传递函数系数。经过在实际装置中的测试，获得了良好的滤波效果。

数字滤波器；采样周期；FDAtool；零极点；系数微调

0 引 言

数字滤波器所具有的运用灵活方便，幅频、相频特性可以分别给出等优点，使得利用程序实现的数字滤波器成为信号处理的主要手段之一[1]。常用的数字滤波器有无限冲击响应数字滤波器(IIR)和有限冲击响应数字滤波器(FIR)。IIR输出为过去输出与现时输入的加权和，计算量远小于FIR，且可借助模拟滤波器进行设计，有大量图表可查，方便简单，但其幅频特性受采样周期的影响很大，存在混迭效应；FIR相位线性，但要取得好的衰减特性，一般阶次要高[2-4]。在实际产品开发过程中，对计算量、响应时间等有较高的要求，为此一般采用IIR型数字滤波器。在应用IIR数字滤波器时，不同的采样周期对应不同的传递函数系数，且由于其输出与过去输出有关，对系数要求非常高，一旦出现偏差(或舍入误差不合适)，将影响滤波器效果，甚至造成系统不稳定。本文分析了采样周期变化对IIR数字滤波器传递函数中系数的影响，借助于MATLAB仿真软件中的FDAtool工具计算系数，并在SVG控制保护装置的实际程序中应用，通过录波获得滤波效果的偏差，以微调零极点的位置，最终获得此控制系统下理想的滤波性能。

1 IIR数字滤波器原理

采用直接Ⅱ型网络结构(如图1所示)的N阶IIR数字滤波器，其传递函数的标准形式为[5-6]：

(1)

上式具有N个零点zi和N个极点pi。将式(1)写成如下形式：

(2)

若|pi|<1，当z→∞时，H(z)→0，系统稳定，此时极点位于单位圆内；若|pi|>1，当z→∞时，H(z)→∞，系统不稳定，此时极点位于单位圆外。

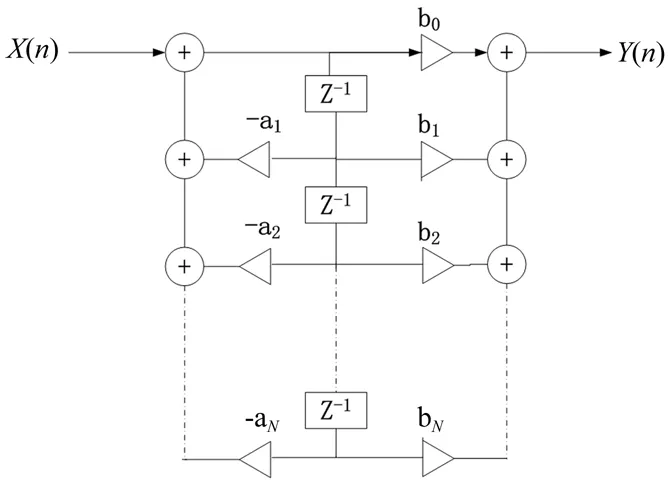
图1 IIR直接Ⅱ型网络结构图

2 采样周期对系数的影响分析

设计IIR低通滤波器，需要知道以下目标参数：采样周期，通带边缘(截止)频率fp，阻带边缘(起始)频率，通带内波动，阻带内最小衰减。设计一个IIR数字滤波器的步骤如图2所示。

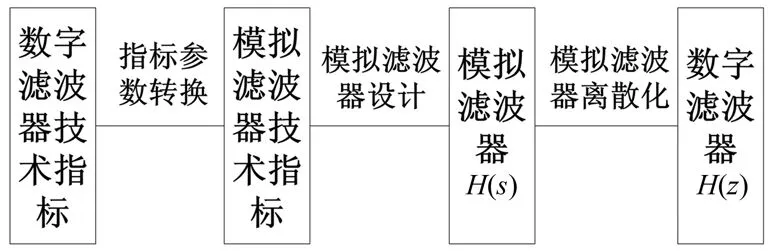
图2 IIR数字滤波器设计步骤示意图

其中采样周期对IIR数字滤波器性能的影响主要体现在模拟滤波器离散化过程中，模拟滤波器的离散化主要有冲击不变变换法和双线性变换法[7]。

模拟滤波器传递函数的标准形式为：

(3)

其中ξi是H(s)在pi处的留数。

对式(3)进行拉普拉斯逆变换，可得：

(4)

对h(t)进行抽样，可得差分方程：

(5)

对式(5)进行z变换即可得数字滤波器的传递函数：

(6)

对比式(3)和式(6)，发现与模拟滤波器极点pi对应的数字滤波器极点为epiTs。由此可见，在IIR数字滤波器设计过程中，传递函数(滤波器性能)受采样频率影响。

在实际应用程序中，数字滤波器的实现依靠其传递函数实现，在已知阶数得到传递函数的标准形式后，获得一组传递函数系数即可完成一个数字滤波器的设计。由式(2)可知，传递函数分母系数ai=epiTs，一旦采样周期发生变化，传递函数的分母系数也要跟着改变。

令原来的采样周期为Ts1，新的采样周期为Ts2，对应的系数为ai1=epiTs1，则pi=(logai)/Ts1，滤波特性不变，则模拟滤波器的极点位置不变。

(7)

3 系数计算

3.1 系数的基本确定步骤

在实际应用中，设计数字滤波器的具体步骤如图3所示。

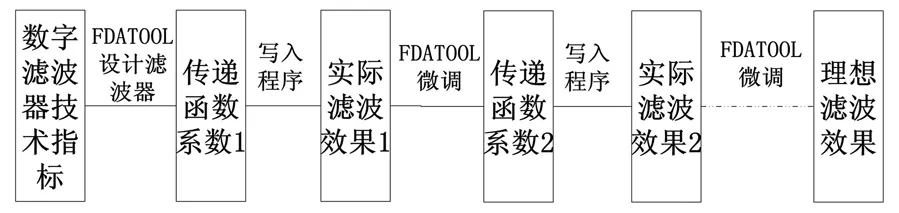
图3 实际应用中数字滤波器的设计过程

由图3 可见，在FDAtool工具中输入目标参数，获得数字滤波器阶数和传递函数系数后，写入实际应用程序中获得的滤波波形会与理想情况下有偏差。这是由于实际程序存在有限字长效应，运算过程中将对系数进行舍入处理，从而引起极点的偏移，这种情况很容易带来稳定性问题，甚至造成寄生振荡。为此，需要在获得系数后，结合程序运行带来的实际效果进行微调，使得系数舍入误差在稳定范围内。

在实际数字滤波器设计过程中，必须进行传递函数系数的微调。本文采用零极点位置微调法，具体为：

1)利用FDAtool工具进行系数计算，同时查看此刻零极点位置，幅频、相频特性曲线(FDAtool界面如图4所示)；

2)与理想的幅频、相频特性曲线进行比较(主要查看截止频率)，如不满足要求，可通过移动零极点位置进行修正，直至获得希望的幅频、相频特性曲线(性能曲线通过图4所示右上角图标查看)；

3)查看滤波器传递函数的各系数ai、bi，写入实际程序后在装置中运行，录波查看数字滤波器输出波形，分析谐波以验证此滤波器性能。若滤波效果不理想，返回第2)步，直至获得理想滤波效果。

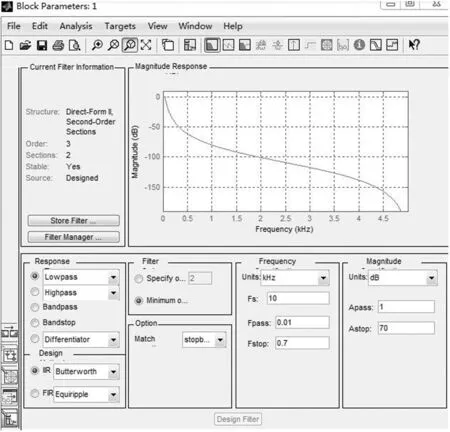
图4 FDAtool工具菜单界面

3.2 仅采样周期变化时系数的确定方法

在SVG开发过程中，发生仅采样周期改变，而滤波性能要求不变的情况，可以通过两种方式获得新的传递函数系数：

1)在第一步通过目标参数获得原始传递函数系数时，即输入新的采样周期，而后按照3.1节所述步骤进行滤波器设计；

2)根据式(7)获得传递函数系数，再利用零极点位置微调获得较为理想的滤波器。

4 零极点微调方法

在系数计算部分已经提到，在根据目标参数获得滤波器阶数和传递函数原始系数后，需要通过微调零极点位置获得相对理想的滤波效果。FDAtool调整零极点位置的界面如图5所示。

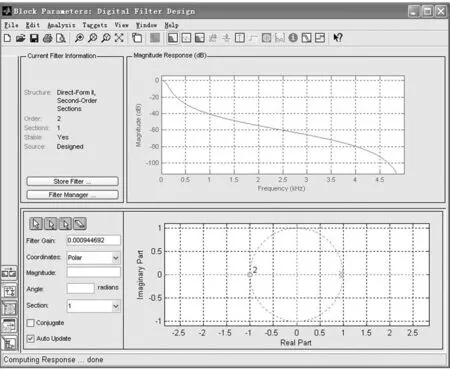
图5 零极点位置调整界面

零极点的个数与滤波器阶数有关，此处为系数微调，为此一般零极点的个数保持不变，仅通过移动零极点位置完成调整。如图5所示，界面上半部分显示幅频特性曲线，界面下半部分为零极点调整界面，零极点位置发生改变后，可在上半界面的特性曲线中查看截止频率等信息。

零极点位置微调过程中可参考如下规律：

1)极点必须在单位圆内部；

2)单位圆附近的零点会在滤波器幅频特性的相应频率处产生陷落，零点离单位圆越近，陷落越深；

3)单位圆附近的极点会在滤波器幅频特性的相应频率处产生凸峰，极点离单位圆越近，凸峰越高。

5 实验验证

SVG控制程序中，采样周期为10 kHz，主要使用低通滤波器，阶数一般为1或者2，以图6(a)所示波形为例进行滤波，设计一个截止频率为80 Hz左右的IIR数字滤波器。在MATLAB的FDAtool中输入数字滤波器的目标参数，可得滤波器阶数为2，该滤波器传递函数的系数为：b0=0.000 609 854 7，b1=0.001 219 709 4，b2=0.000 609 854 7；a0=1，a1=-1.928 942 26，a2=0.931 381 68。

将此组系数写入程序中的二阶滤波器函数，对输出波形录波后发现，高频谐波含量明显下降，但2次谐波增大。可见，此组系

数在本控制系统中不合适，引起了共振，为此进行零极点位置微调，最终获得较为理想的波形，此时的系数为：b0=0.000 537 169 8，b1=0.001 074 339 6，b2=0.000 537 169 8；a0=1，a1=-1.933 380 2，a2=0.935 528 9。滤波前后的波形及谐波含量情况分别如图6～图9所示。

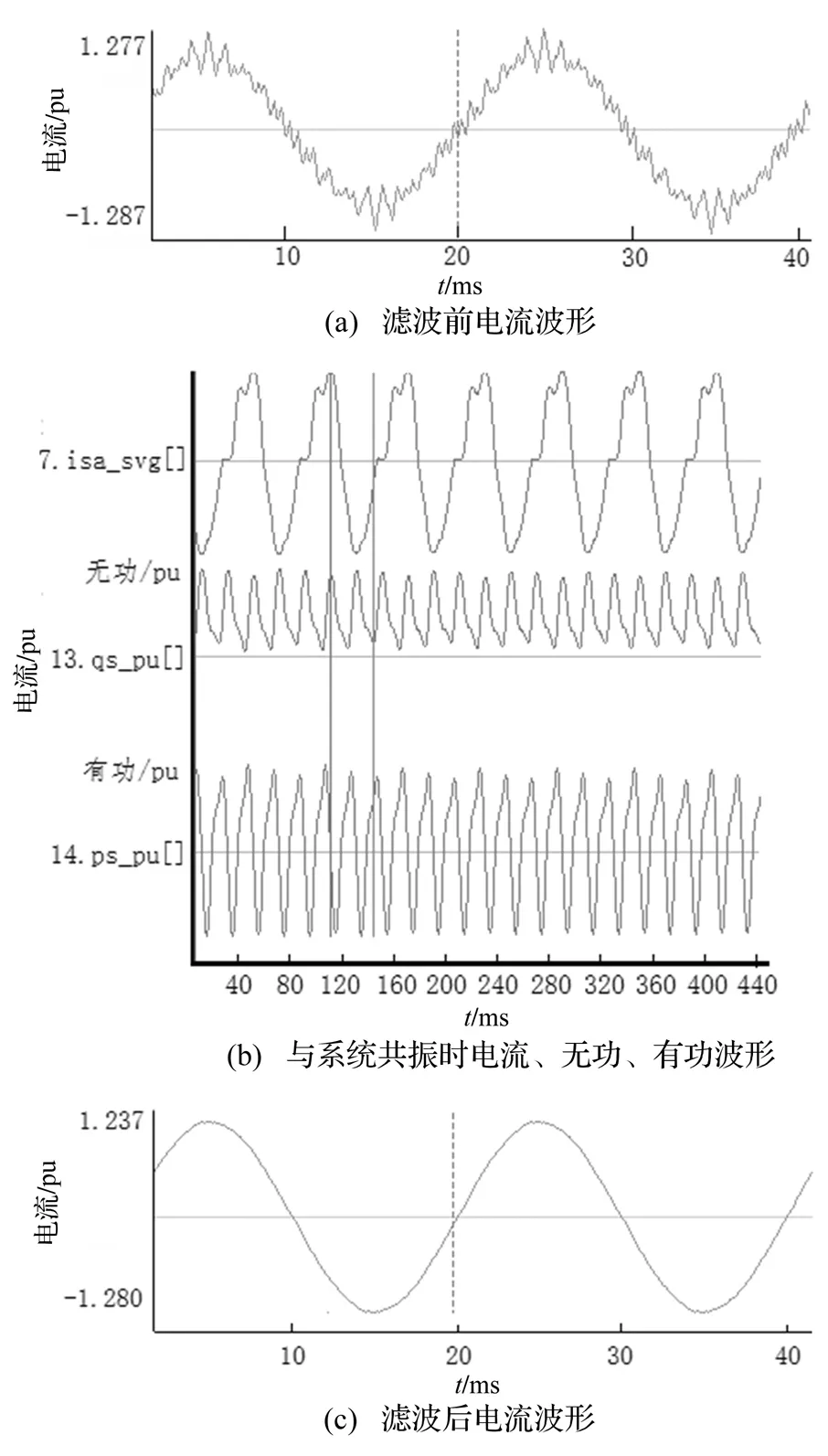
图6 滤波前后电流波形及其谐波含量分析

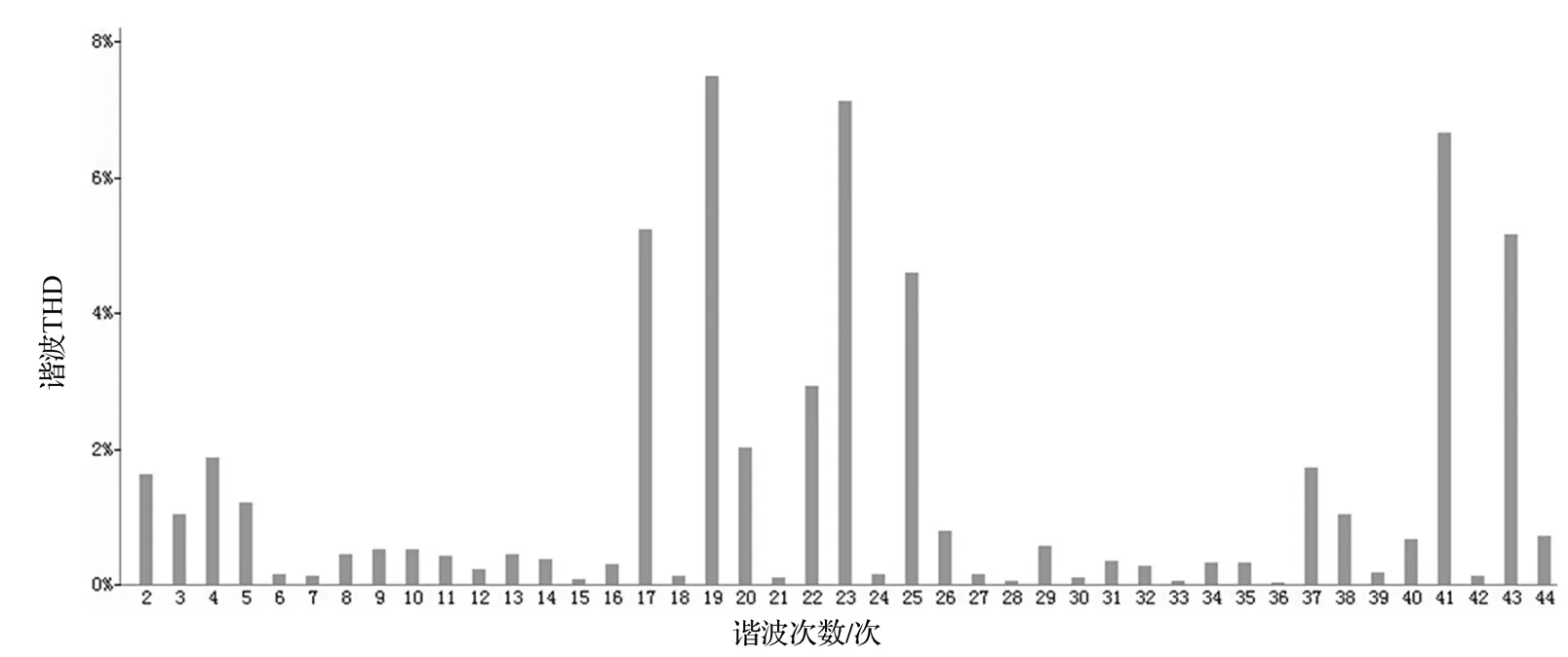
图7 滤波前谐波含量分析

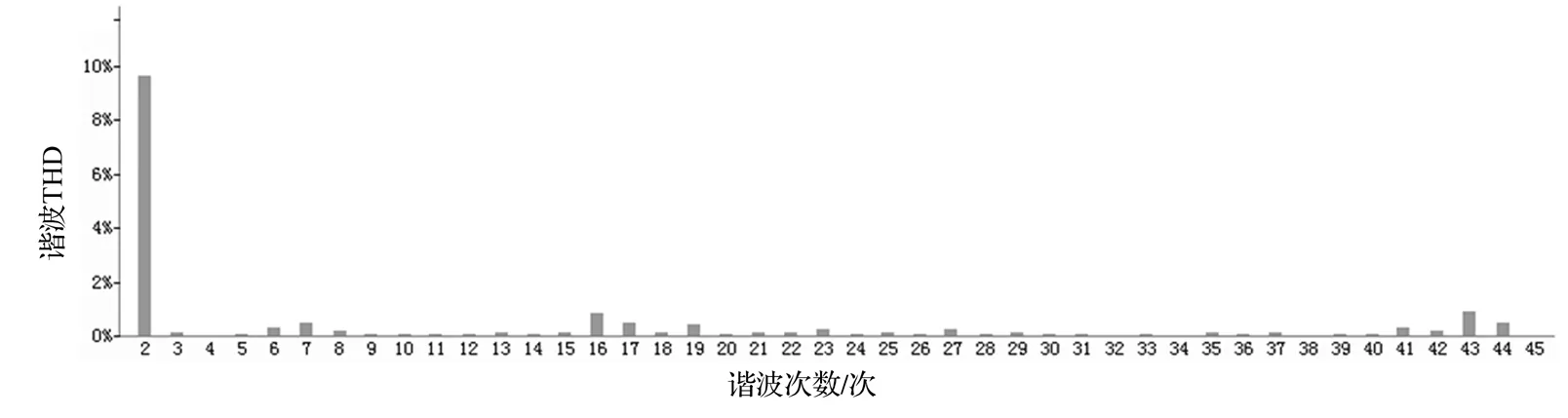
图8 与系统共振时谐波分布

图9 谐波后谐波含量分布

采样周期变为9 kHz，传递函数的系数为：b0=0.000 660 779，b1=0.001 3215 58，b2=0.000 660 779；a0=1，a1=-1.925 984，a2=0.928 627，获得的滤波后波形如图10所示。

图10 采样周期为9 kHz时，滤波后电流波形

6 结束语

利用MATLAB软件中的FDAtool工具可简化IIR型数字滤波器的设计步骤，而结合实际录波获得的滤波效果，进行零极点位置微调则简单直观的抵消了有限字长带来的混迭效应，获得理想的滤波效果；采样周期对传递函数的系数有影响，通过系数调整，可获得相同的滤波效果。数字滤波器应用广泛，分析采样周

期对传递函数系数的影响、掌握其实用设计技术，具有深刻的意义。

[1] 王小艳.静止无功发生器的电流检测和控制策略研究[D].西安：西安理工大学,2010.

[2] 王群,姚为正,王兆安.高通和低通滤波器对谐波检测电路检测效果的影响研究[J].电工技术学报,1999,14(5):22-26.

[3] 周柯,罗安,夏向阳,等,一种改进的id-iq谐波检测方法及数字低通滤波器的优化设计[J].中国电机工程学报,2007,27(34):96-101.

[4] 程远楚,徐德鸿,刘燕,等.基于瞬时无功理论的svc低通滤波器设计与应用[J].电工技术学报，2008, 23(9):138-143.

[5] 胡广书. 数字信号处理—理论算法与实现[M]. 2版.北京:清华大学出版社,2003.

[6] 丁玉美,高西全.数字信号处理[M].西安:西安电子科技大学出版社,2005.

[7] 刘翔宇,杨仁刚,王文成.基于id-iq法谐波检测中数字低通滤波器的设计及其DSP实现[J].电力自动化设备,2006,26(8):51-54.

Practical Design of a Digital Filter Based on SVG Control Application

Fang Cunyang, Shi Shengdan

(NARI Technology Co., Ltd., Nanjing Jiangsu 211106, China)

IIR digital filters find wide application in signal processing through software thanks to their excellent attenuation characteristics. With regards to IIR digital filters used in the development of application programs for the control protection device for Static Var Generator (SVG), FDAtool in Matlab is used to provide the order number and transfer function coefficient, a quite ideal amplitude-frequency curve is obtained through fine-tuning of the pole zero position in the tool, and the output coefficient is written into the function of the control program. This paper further analyzes the effect of sampling period upon pole zero position of the filter. For different sampling periods, the digital filter’s pole zero position differs from each other, thus generating a new transfer function coefficient. A good filtering effect is achieved as shown in the test on actual devices.

digital filter; sampling period; FDA tool; pole-zero; coefficient fine-tuning

10.3969/j.issn.1000-3886.2016.06.009

TN713+.7

A

1000-3886(2016)06-0027-04

方存洋(1968-)，男，安徽人，本科，工程师，主要研究方向：电力电子无功补偿技术。

定稿日期: 2016-06-09