活性药型罩聚能装药作用混凝土靶毁伤效应

张雪朋， 肖建光， 余庆波， 郑元枫， 王海福

(北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

活性药型罩聚能装药作用混凝土靶毁伤效应

张雪朋， 肖建光， 余庆波， 郑元枫， 王海福

(北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

采用数值模拟和地面静爆实验相结合的方法，对活性药型罩聚能装药作用混凝土靶毁伤效应问题进行了研究. 在Autodyn数值模拟中，活性药型罩爆炸驱动形成射流及侵彻混凝土靶过程采用二维欧拉算法，活性射流侵入混凝土内爆破过程采用三维SPH算法，活性射流冲击反应由Powder Burn模型描述，通过算法转换实现分步连续数值模拟. 数值模拟结果表明，与金属射流相比，活性射流终点效应受炸高的影响更敏感，在约为1.0倍装药直径炸高下，活性射流可显著发挥侵爆联合毁伤优势，有效爆破深度约为6.5倍装药直径，当炸高超过2.0倍装药直径后，侵爆毁伤效应显著减弱. 进一步与地面静爆实验结果相比，两者基本相吻合，验证了数值模拟的有效性.

聚能装药；活性药型罩；混凝土靶；数值模拟；毁伤效应

活性材料技术作为当前高效毁伤领域的热点研究方向之一，受到了世界各国的广泛关注和大力研究[1-4]. Baker E L等[5]采用脉冲X光技术研究了活性药型罩聚能装药在爆炸驱动下活性射流的成型行为，并通过地面静爆实验研究了活性材料配方对混凝土靶毁伤效应的影响；Daniels A S等[6]通过实验研究了炸高对活性药型罩聚能装药作用混凝土靶的影响规律[5-6]. 从国内外公开发表的文献看，有关活性药型罩聚能装药侵爆行为研究主要体现在实验研究和机理分析两个方面[7-9]，而活性射流爆炸效应的数值模拟未见公开发表. 随着Autodyn中Powder Burn模型的推出，使实现活性药型罩聚能装药对混凝土靶侵爆效应数值模拟成为可能. 本文采用数值模拟和地面静爆实验相结合的方法，对活性药型罩聚能装药作用混凝土靶毁伤效应进行了研究.

1 数值方法

1.1 活性材料冲击反应模型

合理选用活性材料冲击反应模型，是实现活性材料药型罩聚能装药侵爆毁伤效应数值模拟的关键. 为有效描述活性材料药型罩在聚能装药爆轰驱动下的化学响应行为，本文采用主要用于描述火药爆燃反应的Powder Burn模型，近似描述活性材料冲击反应行为. 反应率和燃烧速率是Powder Burn模型用于表征反应压力的两个主要参数. 反应率F与时间t的关系可表述为

(1)

式中：m(t0)为初始时刻活性材料的质量；m(t)为活性材料经过时间t后剩余质量.

活性材料爆燃产物气体压力方程可表述为

(2)

式中：ρg为活性材料密度；eg为单位质量活性材料的含能量，D为常数.

燃烧速率b(pg)与气体压力pg关系为

(3)

这样，活性材料的反应速率可表述为

(4)

式中G，c，α为与活性材料颗粒特性有关的常量[7]. 活性材料有关参数列于表1，表中ρ0，cp，G，A，B，C，n，θ和c0分别为活性材料的密度、比定压热容、剪切模量、屈服强度、应变硬化模量、应变率强化参数、硬化指数、温度软化指数和声速.

表1 活性材料参数

1.2 活性射流成型及侵爆算法

不同于金属药型罩，活性药型罩在爆轰波加载下射流形成行为、侵彻过程及爆炸效应要复杂得多，采用单一算法无法有效模拟活性射流的侵爆行为. 为在Autodyn中实现活性射流对混凝土靶的侵爆效应数值模拟，假设活性射流形成过程和侵彻阶段为惰性，侵彻结束后活性射流发生爆炸反应. 基于以上假设，通过Euler-SPH算法转换，实现活性药型罩聚能装药作用混凝土靶侵爆行为的分步连续计算. 首先，采用二维Euler算法计算活性药型罩聚能装药的射流成型及侵彻行为；其次，当侵彻结束后，把活性射流和混凝土靶转换成三维Lagrange算法，并将Powder Burn模型加入活性射流材料模型；最后，将Lagrange算法转换成SPH算法. 在算法转换和连续计算过程中[9]，除了加入活性材料冲击反应Powder Burn模型外，同时还保留了活性射流侵彻混凝土靶引起的毁伤效应，从而有效解决了活性射流作用混凝土靶侵彻-爆炸联合毁伤数值模拟问题. 有关算法转换如图1所示.

图2所示为活性药型罩聚能装药作用混凝土靶不同时刻毁伤效应典型数值模拟结果. 图2(a)和图2(b)为活性射流侵彻混凝土靶阶段典型损伤云图，DAMAGE的取值范围是0～1，其中0代表完好无损，1代表完全破坏. 从图中可以看出，活性射流侵彻阶段对混凝土靶损伤区域较小，只是沿侵彻孔四周有些细小的裂纹，随着侵深逐渐增加，混凝土靶损伤加重且裂纹增长，并向四周扩散. 图2(c)和图2(d)为活性射流在侵孔内爆炸阶段混凝土靶典型损伤云图，从图中可以看出，活性材料爆炸后，首先在侵彻孔位置形成破碎区并不断向外扩展，对混凝土靶造成抛掷爆破. 由于混凝土靶是有限靶，当爆炸冲击波到达混凝土靶界面后，爆炸冲击波卸载形成的拉应力超过混凝土抗拉强度后，在混凝土靶上形成一个环向剪切环，混凝土靶被爆炸冲击波沿着裂纹撕裂并抛掷出去.

2 数值模拟结果及分析

对不同炸高下活性药型罩聚能装药作用混凝土靶毁伤效应进行了数值模拟，不同炸高条件下混凝土靶侵彻深度和爆破深度数值模拟结果列于表2，相应的混凝土靶毁伤效应云图如图3所示.

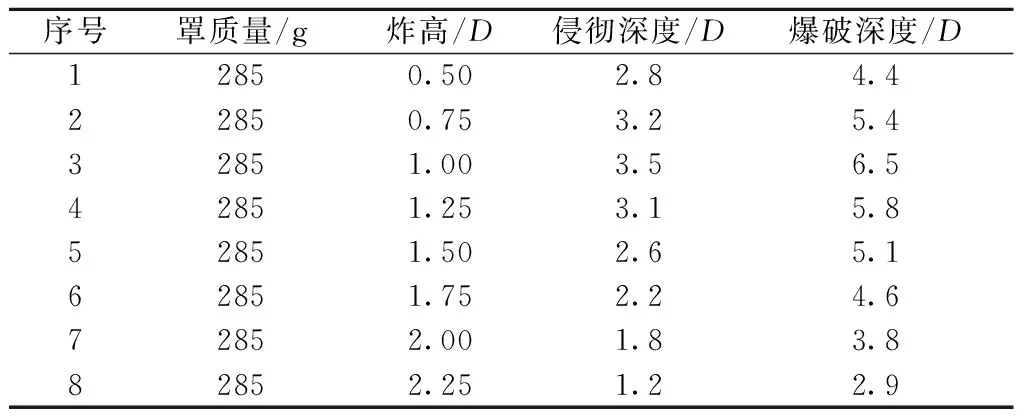
表2 数值模拟结果

由表2可以看出，随着炸高增大，活性药型罩聚能装药对混凝土靶的侵彻深度先增大后减小，与金属射流相比，活性射流侵彻性能受炸高的影响要敏感得多，在1倍装药直径炸高下，活性材料射流可显著发挥侵爆联合毁伤优势，有效爆破深度可达6.5倍装药直径以上，但当炸高超过2.0倍装药直径后，侵彻性能显著减弱. 活性药型罩聚能装药对混凝土靶的侵彻-爆炸联合毁伤效应由侵彻深度和进入侵孔内活性材料质量共同决定的. 在小炸高条件下，虽然侵彻阶段侵深不足，但进入侵孔内活性材料质量足够多，侵爆联合毁伤效应显著；在大炸高条件下，侵彻阶段侵深不足，且进入侵孔内的活性材料质量也较小，相应的侵爆联合毁伤效应就弱.

从图3中可以看出，活性材料在混凝土靶侵彻孔内爆炸后，在混凝土靶中形成冲击波，相接触的混凝土被强烈压缩，形成了压缩粉碎区域. 随着冲击波在混凝土中传播，混凝土质点产生相应的径向位移，构成径向压应力和切向拉应力的应力场. 当介质所受的切向拉应力大于混凝土的抗拉强度时，该处混凝土被拉断，形成与粉碎区域贯通的径向裂隙. 爆轰产物的膨胀尖劈作用助长了径向裂隙的扩展，爆生气体膨胀的同时其压力相应下降. 随后，由于惯性运动，侵彻孔周围的混凝土在压缩过程中累积弹性变形能，混凝土介质体继续朝着远离侵彻孔方向运动，结果导致空腔里的爆炸产物出现负压，达到其极限程度后，弹性能释放形成径向稀疏波，产生与压应力波作用反向的拉应力，介质质点出现反方向运动. 当此处所受的拉应力大于混凝土的抗拉强度时，混凝土体被拉断，形成环向裂隙. 随着径向裂隙的扩展与变向，加上破坏区与片落区连接形成连续性的破坏，其逐渐与自由面贯通，部分混凝土介质以一定的初速度被抛掷出去，形成抛掷漏斗坑.

另外，由图3可见，当炸高超过2.0倍装药直径时，活性药型罩聚能装药对混凝土靶的侵爆联合毁伤效应显著减弱，这是因为活性射流在大炸高条件下更易发生分散、断裂现象，对混凝土靶的侵彻能力降低，只有很少一部分活性材料在侵彻孔内发生反应，而相当多质量的活性材料在混凝土靶表层发生爆炸反应，活性材料释放的能量没有得到很好利用.

3 数值模拟有效性的实验验证

3.1 实验方法

为验证数值模拟结果的有效性，进一步对活性药型罩聚能装药的毁伤效应进行了实验研究. 其中，活性药型罩聚能装药直径为90 mm，C35圆柱形混凝土靶结构尺寸为Φ1 200 mm×1 000 mm，周侧带有5 mm厚钢箍，通过炸高筒进行装药炸高调节.

3.2 实验结果与分析

不同炸高条件下活性药型罩聚能装药作用混凝土靶毁伤效应的典型实验结果如图4所示. 当活性药型罩聚能装药以0.5倍装药直径的炸高作用混凝土靶时，混凝土靶毁伤效应如图4(a)所示，混凝土靶在活性射流爆炸后被爆炸冲击波剪切破坏，形成一个不规则的剪切环，且四周加固的钢箍被抛掷出去. 混凝土靶中心位置比环向位置稍高，这是因为爆炸冲击波是沿着侵彻孔的法线方向在混凝土靶内传播，从而使得周向剪切环要低；当活性药型罩聚能装药以1倍装药直径的炸高作用混凝土靶时，混凝土靶毁伤效应如图4(b)所示，混凝土靶完全破碎，形成大块碎块，加固的钢箍也被活性材料爆炸后形成的冲击波撕裂成若干块. 活性聚能装药在1倍装药直径的炸高时对混凝土靶的侵彻深度最大，当活性射流在侵彻孔内爆炸后，在混凝土靶内形成的破碎区已经超过了混凝土靶的边界，所以使得混凝土靶完全发生结构破坏；当活性药型罩聚能装药以1.5倍装药直径的炸高作用混凝土靶时，混凝土靶毁伤效应如图4(c)所示，混凝土靶前端一部分被活性材料的爆炸冲击波粉碎抛掷出去，还有一部分发生碎裂，由于有钢箍固定，没有被抛掷出去. 这是由于活性射流在1.5倍装药直径的炸高下对混凝土靶的侵彻深度较小，活性材料爆炸后的爆炸冲击波在混凝土靶径向方向传播，当遇到混凝土靶边界时，爆轰波卸载以后混凝土靶发生碎裂.

数值模拟结果与实验值对比如图5所示. 由图5可见，活性药型罩聚能装药对混凝土靶毁伤效应显著受炸高的影响. 随着炸高增大，活性射流对混凝土靶的侵爆深度呈现先增大后减小的变化趋势，这与金属射流的侵彻规律基本一致，但活性药型罩聚能装药的有利炸高较金属药型罩小得多，约为1.0倍装药直径. 这是因为活性药型罩本质上是一种粉末冶金罩，在爆炸驱动形成射流过程中，受材料延展性影响，活性射流在大炸高下更易发生缩颈和断裂，致使活性药型罩的有利炸高较小，在约为1.0倍装药直径时毁伤效果显著. 当炸高小于1.0倍装药直径时，制约了活性射流的拉长，导致活性射流的侵爆深度随炸高的增大而提高.

从图5还可以看出，数值模拟结果与实验值存在一定差异，这是因为数值模拟过程中假设活性材料在射流形成阶段不发生反应. 事实上，聚能装药起爆后，爆轰波作用在活性药型罩上的平均压力在20 GPa以上，远远超过了活性材料激活起爆压力，致使部分活性材料在射流形成过程中开始反应，一方面，影响活性射流的稳定性，降低侵彻能力；另一方面，活性射流侵入混凝土靶的有效质量减少，减弱了爆破威力，从而导致实验值比数值模拟结果偏低.

4 结 论

① 采用Euler-Lagrange-SPH时序转换分步连续算法，结合活性材料Powder Burn模型，实现了聚能装药爆炸驱动活性药型罩形成射流过程、侵彻混凝土和内爆效应数值模拟.

② 与金属药型罩相比，活性药型罩聚能装药对混凝土靶的毁伤效应受炸高影响更显著，在约为1.0倍装药直径炸高下，可显著发挥侵爆联合毁伤效应，爆破深度约为6.5倍装药直径.

③ 实验结果与数值模拟结果吻合较好，验证了数值模拟的有效性，为活性药型罩聚能装药的侵彻-爆破联合毁伤行为提供一种新的技术途径.

[1] 王海福，刘宗伟，俞为民，等.活性破片能量输出特性实验研究[J].北京理工大学学报，2009，29(8)：663-666.

Wang Haifu， Liu Zongwei， Yu Weimin， et al. Experimental investigation of energy release character-istics of reactive fragments[J]. Transactions of Beijing Institute of Technology， 2009，29(8):663-666.(in Chinese)

[2] 余庆波，刘宗伟，金学科，等.活性破片战斗部威力评价方法[J].北京理工大学学报，2012，32(7):661-664.

Yu Qingbo，Liu Zongwei，Jin Xueke，et al. Method for assessing lethality of reactive fragment warhead[J]. Transactions of Beijing Institute of Technology， 2012，32(7):661-664. (in Chinese)

[3] 王海福，郑元枫，余庆波，等.活性破片引爆屏蔽装药机理研究[J].北京理工大学学报，2012，32(8):786-789.

Wang Haifu，Zheng Yuanfeng，Yu Qingbo，et al. Study on initiation mechanism of reactive fragment to covered explosive[J]. Transactions of Beijing Institute of Technology， 2012，32(8):786-789. (in Chinese)

[4] Raftenberg M N， Mock G C. Modeling the impact deformation of rods of a pressed PTFE/AL composite mixture[J]. International Joumal of Impact Engineering, 2008，35(12):1735-1744.

[5] Daniels A S， Baker E L， DeFisher S E， et al. Bam Bam: Large Scale Unitary Demolition Warheads[C]∥Proceedings of the 23rd Intemational Symposium on Ballistics. Tarragona， Spain： [s.n.], 2007:125-130.

[6] Daniels A， Baker E， Ng K. A Unitary Demolition Warhead[C]∥US Army. Picatinny Arsenal， Mines. Demolition and Non-lethal Weapons Conference. New Orleans， LA:[s.n.], 2003:9-11.

[7] Smestada E， Moxnesb J F， Degardstuena G. Modelling of deflagration， establishing material data into ANSYS Autodyn’s powder burn model[C]∥International Annual Conference. [S.l.]: Fraunhofer Institute FUR Chemische Technology, 2012:53-58.

[8] Cai J， Walley S M， Hunt R J A， et al. High-strain， high-strain-rate flow and failure in PTFE/AL/W granular composites[J]. Material Science Engineering A， 2008，472(1-2):308-315.

[9] 江增荣，纪君，周邦大，等.装药量及炸点深度对反跑道侵爆战斗部毁伤效应影响[J].弹道学报，2011，23(2):101-105.

Jiang Zengrong， Ji Jun， Zhou Bangda， et al. Influence of charge weight and blast depth Journal of Ballistics, 2011,23(2):101-105. (in Chinese)

(责任编辑：刘雨)

Demolition Effect of Reactive Material Liner Shaped Charge Against Concrete Target

ZHANG Xue-peng， XIAO Jian-guang， YU Qing-bo， ZHENG Yuan-feng， WANG Hai-fu

(State Key Laboratory of Explosion Science and Technology， Beijing Institute of Technology， Beijing 100081， China)

Demolition effect of reactive material liner shaped charge against concrete targets was studied with a method combining numerical simulation and ground-based experiment. In the Autodyn simulation， both the formation of reactive material jet and its penetration process were simulated by Euler-2D solver， whereas SPH-3D solver was used for the demolition effect of reactive material jet. The Powder Burn model was employed to describe the deflagration behavior of reactive materials. The whole numerical simulation process was implemented by an Euler to SPH solver transition. The simulation results show that， the influence of stand-off on terminal effect of reactive material jet is greater than that of metal jet. The dramatic demolition effect produced by a combination of penetration and deflagration was achieved at one charge diameter stand-off， corresponding to an effective demolition depth approximate to 6.5 charge diameter. When increasing stand-off beyond two charge diameter， however， the demolition effect of reactive material jet drops off significantly. Moreover， the ground-based experiments are also conducted， and the results show a good fit with numerical simulations.

shaped charge; reactive material liner; concrete target; numerical simulation; damage effect

2015-12-02

张雪朋(1985—)，男，博士研究生，E-mail:3120110147@bit.edu.cn.

王海福(1966—)，男，教授，博士生导师，E-mail：wanghf@bit.edu.cn.

TJ 413

A

1001-0645(2016)12-1211-05

10.15918/j.tbit1001-0645.2016.12.001