颌骨重建手术机器人定位精度分析与误差补偿

孔祥战， 段星光， 王永贵， 赵洪华， 郭传瑸

(1.北京理工大学 智能机器人研究所， 北京 100081；2.济南大学 机械工程学院， 山东，济南 250022；3.北京大学 口腔医学院， 北京 100081)

颌骨重建手术机器人定位精度分析与误差补偿

孔祥战1， 段星光1， 王永贵1， 赵洪华2， 郭传瑸3

(1.北京理工大学 智能机器人研究所， 北京 100081；2.济南大学 机械工程学院， 山东，济南 250022；3.北京大学 口腔医学院， 北京 100081)

为提高颌骨重建机器人的精度，借助于—台可以实现绝对坐标测量的高精度光学定位跟踪仪，对机器人系统的定位精度进行了误差分析与补偿研究. 针对结构参数和运动变量误差，采用修正的运动学模型，进一步真实地反映了机器人的实际结构参数；对齿轮传动误差和间隙引起的关节回转误差通过实验进行了修正，有效提高了关节传动精度；对零位定位误差，通过机器人逆运动学反解出关节转角，并进行误差补偿，提高了定位基准的精度. 实验结果表明上述方法可有效提高颌骨重建机器人的定位精度.

医疗机器人；靶点映射误差；定位精度；零位误差

正颌外科是通过口腔正畸手术的方法矫治牙颌面畸形，使患者不仅牙齿可以咬合，颌面外形还要美观. 正颌手术通过截骨、移植骨将下颌骨块移动，并按咬合功能和脸部整形原则对骨块重新组合、固定，从而恢复正常的颌面形状[1-2]. 然而，传统正颌手术由于技术难度大、手术精度低，难以满足临床需求[3-4]. 颌骨重建手术机器人的临床应用提高了医生的技能，降低了手术劳动强度，提高了手术成功率，具有十分重要的临床意义.

为满足实际临床需要，颌骨重建辅助手术机器人需要具有很高的绝对定位精度[5]，但多数串联机器人的绝对定位精度仅能达到2～3 mm[6-8]. 这种绝对定位精度的情况下，无法满足正颌手术的临床需求. 因此，剖析影响串联机器人精度的原因，并研究如何提高颌骨重建辅助手术机器人的绝对定位精度，具有十分重要的临床意义.

1 系统构成

在国家“八六三”计划项目的资助下，研发了颌骨重建辅助手术机器人系统[9]，其主要包括以下4部分：

① 术前计算机辅助手术规划系统：实现患者头颅的三维重建，正颌手术规划.

② 颌骨重建手术机器人系统：由操作台、光学定位仪和多臂机器人组成. 多臂机器人包括2个把持臂和1个操作臂，左右两侧的把持臂术中把持游离升支，完成对升支的绝对空间定位，中间的操作臂将活的植入体以规划的姿态移动到术前设计的位置.

③ 术后手术效果评估系统：把手术的临床完成情况，借助医生经验进行效果评估.

④ 虚拟手术培训系统：对新医生的正颌手术的技能，在计算机上进行培训.

2 机器人绝对定位精度分析

按照颌骨重建手术操作流程分析，以多臂机器人坐标系为基准，可把影响系统绝对定位精度的因素分为两大类：一类是靶点映射误差，它是术前规划使用的三维头颅模型的图像坐标系映射到多臂机器人坐标系带来的误差，主要包括三维头颅模型重构误差、术前模型和术中模型配准误差、图像坐标系与多臂机器人坐标系之间的坐标变换误差；另一类是多臂机器人本体的误差，它是多臂机器人按照指令以一定位姿实际到达点与理想到达点之间的误差，主要包括机器人结构参数误差、关节传动误差、零位误差.

本文借助于颌骨重建机器人系统中自有的光学导航定位仪，从靶点映射、逆运动学模型、关节回转误差、零位误差4个方面入手，分别提出相应减少误差的方法，并通过实验的方法对系统进行了误差补偿. 实验结果表明，这些方法提高了机器人系统的精度.

3 靶点映射误差分析及其减小措施

整个系统包含4个坐标系：① 头颅模型重建空间，对应图像坐标系{V}；② 患者空间，对应患者坐标系{P}；③ 多臂机器人空间，对应机器人坐标系{R}；④ 光学导航定位仪空间，对应光学测量坐标系{O}. 它们之间的转换关系如图1所示.

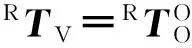
分析图3转换矩阵求解步骤，把目标点在空间的位置变化及误差传递通过有向图[10]表示，如图3所示.

图3 靶点映射误差传递

Fig.3 Target mapping error propagation

图3中：节点V0，V1，V2，V3表示目标点在不同坐标系下的空间位姿；Tcon，Treg，Tcal表示坐标系的变换矩阵；Σcon，Σreg，Σcal表示变换矩阵对应误差的协方差阵. 从有向图可知，靶点映射误差传递属于串联误差链.

因此，要提高整个系统的绝对定位精度需要从头颅模型的三维重建、术前术中模型配准、图像坐标与机器人坐标变换三方面入手. 实际应用中，采用足够小的断层层厚进行CT扫描，多模态二维图像的获取与数据融合，优化断层图像的预处理，图像插值和分割；加入提高配准算法稳健性的判别方法，采用空间配准优化算法；利用4个以上标记点进行实验，统计各个标记点的误差，计算误差分布，估计靶点配准误差，同时降低随机的动态误差等.

4 机器人杆件D-H参数的修正

由于零件加工误差和机器人装配误差的存在，用D-H方法求出的机器人运动学模型，并不能完全真实反映机器人的实际运动. 本文中以多臂机器人中间操作臂为例进行分析，采用一种机器人运动学模型修正方法，对机器人的参数误差进行补偿，以提高机器人定位精度.

机器人标定实验如图4所示，将NDI光学导航定位仪固定，并调整其位置使被测量点处于最佳测量范围内.

实验时，在机器人中间臂的各个臂杆上配上定位球孔. 具体操作步骤如下：

② 同理，调整靶球固定位置，同步骤1可得到圆心C2，重复步骤1，2，可以拟合得到不同圆心，将多个圆心点线性拟合，近似为一条直线Z1(图6).

③ 控制机器人回到初始位置，然后其它关节不动，单独运动第3关节，使得小臂每转动10°记录1次小臂上的靶球位置，拟合出圆心C3.

④ 同理，调整小臂固定靶球位置，重复步骤3，拟合出多个圆心，然后再次拟合出小臂轴线Z2.

通过上述步骤，可以得到大臂关节、小臂关节以及第4关节的轴线，利用空间直线的距离和角度算法，可以求得大臂、小臂的修正臂杆参数.

把测得的数据导入Matlab中，利用最小二乘法依次对各个关节轴线进行拟合求解，求得各个关节的空间轴线方程，两个轴线间的最短距离则为实际杆长参数，求解各空间轴线的夹角即为实际杆件夹角参数. 综上所述机器人各个关节的D-H关节参数调整见表1.

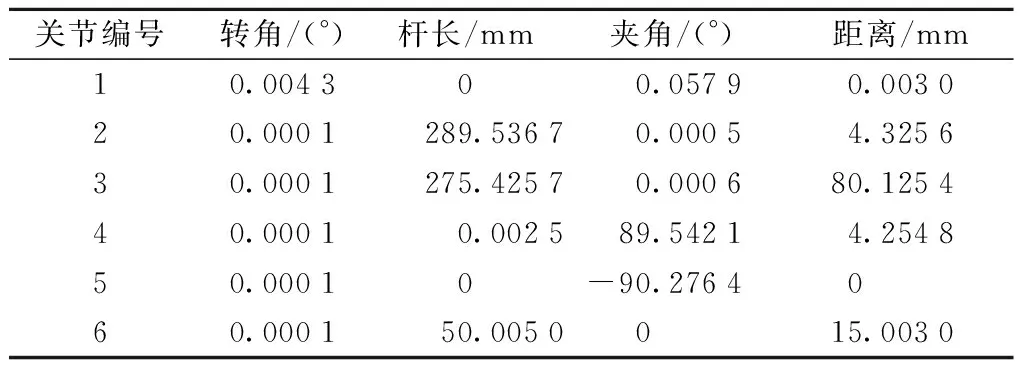
表1 机器人各关节的D-H参数误差

5 关节传动误差分析与补偿

由于传动误差的存在，电机码盘读数并不能准确记录机器人关节的实际运动. 本文用基于Levenberg Marquardt快速数值优化训练算法对机器人关节传动误差进行补偿[11]，以提高绝对定位精度. 机器人各关节的数据训练样本的获取步骤如下：

① 控制机器人一个关节到达零位位置；

② 控制此关节按10°的步长往正向运动，每次运动结束后，用光学导航定位仪测量关节实际转过的角度，直到关节运动到正的极限位置；

INTELLI-RAY400智能控制光固化机系统(深圳市慧烁机电有限公司)；JJ-1000型精密电子天平(美国双杰兄弟集团有限公司)；QTX型漆膜柔弹性试验器(天津永利达材料试验机有限公司)；QXJ型漆膜冲击试验仪(天津永利达材料试验机有限公司)；CMT4204型微机控制万能材料试验机(深圳新三思公司)；摆杆阻尼硬度计(天津永利达材料试验机有限公司)；Nicolet5700智能型傅里叶变换红外光谱仪(美国热电尼高力公司)。

③ 控制此关节回到零位位置；

④ 控制此关节按10°的步长往负向运动，每次运动结束后，用光学导航定位仪测量关节实际转过的角度，直到关节运动到负的极限位置.

由此可以获得各关节正向运动和负向运动的样本数据. 训练前，对样本数据完成尺度变换，使数据落在[0，1]区间内. 训练完成后，将期望关节位置θi和运动方向si作为输入，可获得电机的目标转角θm.

6 零位误差校正与补偿

基于机器人霍尔传感器和电机轴Z脉冲信号，结合零位霍尔传感器和限位传感器的状态，本文提出了一种机器人关节任意初始位置下精确寻找零位的方法，该方法可以提高机器人关节的定位基准精度. 霍尔传感器实现高精度零位定位需具备前提条件，即霍尔传感器实际位置要与设计的位置一致，但传感器在安装中必然存在一定的装配误差，因此，修正机器人的杆件参数后，还需对零位传感器位置进行误差补偿.

机器人零位误差补偿的数学模型为

(1)

7 定位精度实验

为验证机器人修正运动学模型、关节传动误差和关节零位传感器误差补偿效果，借助高精度且可以实现绝对坐标测量的NDI光学导航定位系统，对校正后的机器人绝对定位精度进行了实验研究.

实验中，分别选取机器人工作空间内的12个点进行位置精度测试. 导航定位仪对测量范围内的点的测量平均误差小于0.25 mm，在最佳位置小于0.1 mm. 实验的具体步骤如下：

① 机器人初始化. 通过安装在机器人固定位置的定位支架，完成机器人和光学定位仪之间的坐标配准，得到光学定位仪坐标系与在机器人坐标系的转换关系.

② 在机器人坐标系空间内，先给定一个预定点的坐标值，作为理想值.

③ 使末端定位支架以预定点为规划点，控制机器人运动，停止后，记录下末端定位支架实际到达点在导航定位仪下的坐标，并结合第一步将该坐标转换至机器人空间，得到相应的机器人空间坐标，记录下该坐标值，即实际值.

④ 重复上述过程，使机器人依次到达不同的预定点，得到多组测的数据，并对数据进行处理.

分别按上述3种模型按照以上步骤控制机器人运动到各个点，将测量得到的结果与理想值相比较，实测点与目标点之间的差即为该点处机器人的绝对定位误差. 测量结果表明，采用D-H 参数的运动学模型[12]，机器人绝对定位误差平均值为7.81 mm，采用修正后的运动学模型，变为3.26 mm；对各关节传动误差进行补偿后，机器人绝对定位误差平均值为2.68 mm，补偿后，变为1.47 mm；实验表明，运动学模型修正、关节误差补偿和零位误差补偿有效地提高了机器人的绝对定位精度.

8 结 论

介绍了颌骨重建辅助手术机器人的整个系统构成，并分析了影响机器人绝对定位精度的各种因素. 针对杆件的长度、空间夹角存在偏差的情况，采用修正的运动学模型代替原来的D-H运动学模型，更加真实地反映了机器人的运动学情况；对齿轮传动误差和间隙引起的关节传动误差进行了补偿，有效提高了关节传动精度；针对零位传感器安装位置出现的偏差，结合机器人运动学模型反解出关节转角进行补偿，有效提高了零位定位基准.

最后，利用光学导航定位仪对机器人绝对定位精度进行了实验研究. 结果表明，对机器人运动学模型的修正，对关节传动、零位定位误差的补偿，提高了机器人的绝对定位精度. 本文采用的方法不仅可以用于提高颌骨重建辅助手术机器人的绝对定位精度，还可以推广到其它串联型机器人.

[1] Hassfeld S， MüHling J. Computer assisted oral and maxillofacial surgery-a review and an assessment of technology[J]. International Journal of Oral and Maxillofacial Surgery， 2001，30(1):2-13.

[2] Foley B D， Thayer W P， Honeybrook A， et al. Mandibular reconstruction using computer-aided design and computer-aided manufacturing: an analysis of surgical results[J]. Journal of Oral and Maxillofacial Surgery， 2013，71(2):e111-e119.

[3] 杜志江，孙立宁，富历新.医疗机器人发展概况综述[J].机器人，2003，25(2):182-187.

Du Zhijiang， Sun Lining， Fu Lixin. An overview of medical robots[J]. Robot， 2003，25(2):182-187. (in Chinese)

[4] Pavlíková G， FoltáN R， Horká M， et al. Piezosurgery in oral and maxillofacial surgery[J]. International Journal of Oral and Maxillofacial Surgery， 2011，40(5):451-457.

[5] De Ceulaer J， De Clercq C， Swennen G R J. Robotic surgery in oral and maxillofacial， craniofacial and head and neck surgery: a systematic review of the literature[J]. International Journal of Oral and Maxillofacial Surgery， 2012，41(11):1311-1324.

[6] Borumandi F， Heliotis M， Kerawala C， et al. Role of robotic surgery in oral and maxillofacial， and head and neck surgery[J]. British Journal of Oral and Maxillofacial Surgery， 2012，50(5):389-393.

[7] Hultman E， Leijon M. Six-degrees-of-freedom (6-dof) work object positional calibration using a robot-held proximity sensor[J]. Machines， 2013，1(2):63-80.

[8] Kim J， Jung K. Positioning accuracy improvement of laser navigation using unscented Kalman filter[M]∥Intelligent Autonomous Systems 12. Berlin, Heidel-berg: Springer， 2013:807-816.

[9] Syed A A， Duan X， Kong X， et al. Maxillofacial surgical robotic manipulator controlled by haptic device with force feedback[C]∥Proceedings of Complex Medical Engineering (CME)， 2013 ICME International Conference on IEEE. [S.l.]: IEEE, 2013:363-368.

[10] 丁洪生，黄志晨，刘永俊，等.一种串联机器人的随机误差分析方法[J].北京理工大学学报，2014,3(9):892-896.

Ding Hongsheng, Huang Zhichen, Liu Yongjun, et al. A random error analysis method for serial robot[J]. Transactions of Beijing Institute of Technology, 2014,3(9):892-896. (in Chinese)

[11] 王强，张之敬，叶鑫，等.微装配检测棱镜机构方位调整及误差分析[J].北京理工大学学报，2011，31(8):896-900.

Wang Qiang, Zhang Zhijing, Ye Xin, et al. The position adjustment and error analysis of detection prism mechanism for micro-assembly system[J]. Transactions of Beijing Institute of Technology, 2011,31(8):896-900. (in Chinese)

[12] 王建中，齐伟伟，宋遒志，等.基于一种新误差模型的移动机器人模糊控制[J].北京理工大学学报，2006，26(3):244-247.

Wang Jianzhong, Qi Weiwei, Song Qiuzhi, et al. Mobile robot fuzzy control based on a new error model[J]. Transtactions of Beijing Institute of Technology, 2006,26(3):244-247. (in Chinese)

(责任编辑：刘雨)

Positioning Accuracy Analysis and Error Compensation of Medical Robot Assisted for Mandible Reconstruction Surgery

KONG Xiang-zhan1， DUAN Xing-guang1， WANG Yong-gui1，ZHAO Hong-hua2， GUO Chuan-bin3

(1.Intelligent Robotics Institute， School of Mechatronical Engineering， Beijing Institute of Technology，Beijing 100081, China; 2.College of Mechanical Engineering， University of Jinan， Jinan，Shandong 250022, China; 3.Peking University of Stomatology， Beijing 100081, China)

In order to improve the accuracy of the mandible reconstruction robot， the positioning accuracy and error compensation was studied using NDI Polaris based on analysis of surgery procedure. The kinematics parameters were identified based on a revised D-H kinematics model， taking small distortions of the joint axes and link parameter into consideration. Joint transmission error and zero position error were compensated with experiments. Absolute positioning accuracy of the robot was measured using an accurate NDI Polaris measure device according to the model. The experiment results show that the maximum value and the mean value of the absolute positioning accuracy are much better than the previous values after compensating the errors caused by link parameter， transmission and zero position. The method can be widely used in series robot error compensation.

medical robot; target mapping error; positioning accuracy; zero position error

2015-01-20

国家自然科学基金资助项目(61375106)；国家“八六三”计划项目(2012AA041606)

孔祥战(1983—)，男，博士后，E-mail:ailiyakony@bit.edu.cn.

TP 242.3

A

1001-0645(2016)12-1248-06

10.15918/j.tbit1001-0645.2016.12.008