基于外弹道模型的导电纤维丝束落点散布研究

张广华， 冯顺山

(北京理工大学 机电学院，北京 100081)

基于外弹道模型的导电纤维丝束落点散布研究

张广华， 冯顺山

(北京理工大学 机电学院，北京 100081)

为研究短路毁伤元-导电纤维丝束的落点散布规律，根据子母弹抛撒外弹道理论和丝束展开及飘落运动特性，并重点考虑到丝束运动过程中抛撒速度的散布对其落点的影响，建立了丝束从抛撒到落地的外弹道模型. 通过蒙特卡洛法选取丝束抛撒过程中的抛撒速度并代入模型进行了求解. 计算结果表明，丝束散布范围、散布半径等参量与飞行试验结果基本吻合，证明了本模型具有应用参考价值.

导电纤维丝束；外弹道；软毁伤；落点散布

电力系统是现代战争中的高价值目标，导电纤维弹属于软杀伤弹药，用于攻击敌方高压线、变电站等露天高压电力系统. 中国从20世纪90年代中期开始了导电纤维弹的研制工作. 1999年至今，北京理工大学冯顺山教授领导的科研团队深入开展了导电纤维弹的技术研究，取得了重大进展[1-2].

导电纤维弹通过导电丝束对电力系统进行接触式短路毁伤. 导电丝束最初以丝团的形式装填在导电纤维子弹中，每个母弹中装填若干枚导电纤维子弹，每个子弹中装填几十到上百个丝团. 丝团抛撒出去后一边展开一边飘落，最后，展开的导电丝束搭落在电力系统上对其产生短路毁伤及封锁效应. 导电丝束终端弹道情况分析表明，丝束的落点散布情况直接影响着对电力目标的有效覆盖程度及封锁效能，对导电纤维子母战斗部设计具有重要意义. 因此，本文结合子母弹抛撒外弹道理论及丝束运动特性[3-5]，对丝束落点散布进行了研究.

1 弹道模型的建立

1.1 丝团结构

丝团是导电丝束的初期形式，图1所示为本文所研究丝团的展开结构图.

1.2 丝束空中运动特征

丝束空中运动过程分为2个阶段，各阶段运动特征如下：丝团从子弹中抛出去后获得初速，阻力叶片在抛撒力和气动力作用下从丝轴上张开并带动丝束逐步展开，已展开丝束在惯性力、气动力、重力及风力的联合作用下一边继续展开一边飘落，此为运动的第1阶段，该阶段运动包括丝束的展开和飘落；第2阶段为已全部展开的丝束在气动力、重力及风力作用下的飘落运动，直至丝束搭挂在目标或落在地面上.

1.3 假设条件

丝束空中运动过程中的受力情况比较复杂，为了建立其空中运动外弹道模型，做如下假设：① 丝束运动过程中所有变量均相互独立；② 不考虑抛撒丝团时子弹流场对丝束运动的影响以及丝束间的相互气动干扰；③ 抛撒丝团瞬时子弹攻角为0；④ 已展开的丝束作刚性处理；⑤ 丝束飘落过程中，只受到水平风的作用，且风力保持不变.

1.4 坐标系

为了描述丝束的运动，建立3个坐标系如图2所示.

图中，O-xyz，O1-x1y1z1和O1-x2y2z2分别为地面坐标系、平动坐标系和弹体坐标系.O1为抛撒时刻子弹的质心，O为子弹质心在地面上的投影，O1x2轴与子弹轴线重合，Ox轴为O1x2轴在地面的投影，Oz，O1z1轴垂直于地面向上. 弹体坐标系由平动坐标系绕O1y1轴旋转θ角所得，θ角为弹道倾角，h为抛撒高度. 地面坐标系与弹体坐标系间的速度转换关系如式(1)所示.

(1)

1.5 外弹道模型

1.5.1 第1阶段外弹道模型

通过对导电丝束第1阶段的运动特性进行分析，将该阶段运动分为3部分，得到其在地面坐标系下的外弹道模型如下.

① 丝团展开模型.

丝团展开过程示意图如图3所示.

根据图3所示，得到丝团展开模型为[6]

(2)

式中:l为丝束展开长度；R为缠绕在丝轴上的未展开丝束构成的丝团半径；β′为丝束展开角速度；d为丝束直径；a为丝轴长度；vz,vsz分别为未展开丝团(含丝轴)、已展开丝束在z轴方向的速度；ε为丝束与z轴夹角；J为转动惯量；fyz，fsz，ftz分别为叶片、丝束、丝团在z轴方向所受空气阻力；fyx，fsx，ftx分别为叶片、丝束、丝团在x轴方向所受空气阻力；Gy，Gs，Gt分别为叶片、丝束及丝团重力，Gs=msg=lρlg，Gt=mtg=(mz-lρl)g，ρl为丝束线密度，ms为已展开丝束的质量，mt为未展开丝团质量，mz为丝团总质量.

② 未展开丝团的运动模型.

未展开丝团包括丝轴及缠绕在丝轴上的还未展开丝束，其外弹道模型如式(3)所示.

(3)

式中：vx，vy，vz分别为未展开丝团在3个坐标方向的运动速度；Ctx，Cty，Ctz为阻力系数；Sx，Sy，Sz分别为丝团在3个坐标方向的特征面积；ρ为空气密度；vwx，vwy分别为x轴和y轴方向的风速；vr为相对速度.

③ 已展开丝束的运动模型.

已展开丝束的外弹道模型如式(4)所示.

(4)

式中：vsx，vsy，vsz分别为已展开丝束在3个坐标方向的运动速度；Csx，Csy，Csz为丝束阻力系数；Ssx，Ssy，Ssz为丝束特征面积.

1.5.2 第2阶段外弹道模型

第2阶段运动为丝轴带动已完全展开丝束的飘落运动，由于丝束展开后长达几十米且依然与丝轴连接，因此，以丝轴运动表征丝束的运动. 该段模型如式(5)所示.

(5)

式中：vzx，vzy，vzz分别为丝轴在3个坐标方向的运动速度；Czx，Czy，Czz为阻力系数；Szx，Szy，Szz为特征面积.

2 初始抛撒条件

2.1 初始坐标

丝团在子弹内的装填状态如图4所示.

丝团沿轴向共m列排布，沿径向共n圈排布. 根据图4所示，得到子弹内第i列第j圈中第k个丝团在弹体坐标系下的质心坐标为

(6)

式中:xo为第1列丝团质心在弹体坐标系中的x方向坐标；Rj为坐标原点O1到丝团圆心的距离.

2.2 初始速度

丝团速度v由子弹飞行速度vz、子弹旋转速度vω及子弹抛撒丝团初始速度vp组成，即

(7)

子弹飞行速度vz为

(8)

子弹抛撒丝团示意图如图5所示.

子弹旋转角速度ω及抛撒速度vp会赋予丝团相应的速度vω,vp为

(9)

(10)

可得丝团在弹体坐标系下的速度为

(11)

通过式(1)对式(11)进行相应变换，即可得到丝团在地面坐标系下的初始速度.

2.3 随机参量的选取

导电丝束作为一种柔性杀伤元，空中展开后长达几十米，具有细长柔性索运动的基本运动特征，其飘落过程中会受到风力及风向、抛撒速度等多种因素的影响，因此，若要得到单根丝束的精确落点存在比较大的困难. 但是导电纤维弹中装填有上百个丝团，展开后的丝束会形成覆盖面积很大的导电丝束网，所以其落点散布情况是非常重要的威力参量，单根丝束的精确落点并不十分重要. 因此，通过本文模型对其整体散布进行求解. 丝束展开后长达几十米且依然与丝轴连接，且落地后形成以丝轴为基点、丝束方向与风向重合的丝束威力场. 因此，为了便于描述，本文以丝轴落点表征丝束落点.

靶场地面飞行试验结果显示，丝团抛撒速度vp散布较大，是影响丝束散布的重要因素，其余因素影响相对较小. 为了简化模型，将其余因素固化，vp则通过Monte-Carlo法进行选取.

3 结果分析与讨论

某模拟战斗部，内装400个丝团，丝团抛撒高度h为114.5 m，抛撒速度vp服从均值为160.3，方差为24.72的正态分布，风速为2.5 m/s. 通过本文模型对丝束落点进行计算，结果如图6所示. 通过图6可以看出，通过本文模型计算得出的丝束散布范围与靶场飞行试验结果基本吻合.

通过本文模型进行丝束落点计算时，由于丝团抛撒速度vp在(160.3，24.72)的正态分布内随机选取，所以每次计算都会得到不同的结果，即每次计算都会得到一组散布中心(xs，ys)和散布半径rs. 设丝束落点坐标为(x1，y1)，…，(xi，yi)，…，(xn，yn)，n为丝团个数，则散布中心坐标和散布半径为

(12)

(13)

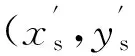
由图7、图8可见，随着模拟次数的增加，当模拟次数大于25次时，散布半径rs和散布中心坐标(xs，ys)的平均值趋于稳定. 实际应用时，可根据精度要求选择合适的模拟次数，以达到模拟精度和计算量的最优化.

4 结 论

本文结合子母弹抛撒经典外弹道理论及导电纤维丝束空中运动特性，建立了导电丝束从抛撒到落地阶段的空中展开及飘落外弹道模型，并通过蒙特卡洛法选取了丝团抛撒速度作为初始值代入模型进行求解，得到主要结论如下：

① 通过本模型求解得到的导电丝束落点散布结果与靶场飞行试验结果基本吻合，可在实际应用中对丝束落点的整体散布情况进行预测；

② 模拟次数直接影响计算结果的精度，当模拟次数大于25次时，散布半径及散布中心点坐标的平均值趋于稳定. 因此，实际应用时，应选择合适的模拟次数，以达到模拟精度和计算量的最优化.

[1] 冯顺山，张国伟，何玉彬，等.导电纤维弹关键技术分析[J].弹箭与制导学报，2004(1):41-43.

Feng Shunshan， Zhang Guowei， He Yubin， et al. Key technology analysis about conductivity fiber bomb[J]. Journal of Projectiles， Rockets， Missiles and Guidance， 2004(1):41-43. (in Chinese)

[2] 梁永直，冯顺山，张广华，等.弹用导电丝束引弧机理及试验研究[J].弹箭与制导学报，2012(6):186-189.

Liang Yongzhi， Feng Shunshan， Zhang Guanghua，et al. Arc mechanism and experimental research of conductive fiber used in weapon[J]. Journal of Projectiles，Rockets，Missiles and Guidance， 2012(6):186-189. (in Chinese)

[3] 房玉军，蒋建伟.子弹药抛撒随机外弹道模型及其蒙特卡洛解法[J].北京理工大学学报，2009，29(10):850-853.

Fang Yujun， Jiang Jianwei. Stochastic exterior ballistic model of submunitions and its Monte Carlo solution[J]. Transactions of Beijing Institute of Technology， 2009，29(10):850-853. (in Chinese)

[4] Shi Jiao， Tang Shengjing， Gao Feng. Mathematical modeling of the bellows dispersion system of submunitions[J]. Journal of Beijing Institute of Technology， 2012，21(1):23-30.

[5] Tan Dacheng， Yuan Zengfeng. Cluster warhead dispersing technique and its interior ballistic calculation[J]. Journal of Beijing Institute of Technology， 2000， 9(3)：273-277.

[6] 张广华，冯顺山，葛超.导电纤维丝团空中展开与飘落运动特性[J].弹道学报，2014(1)：35-39.

Zhang Guanghua， Feng Shunshan， Ge Chao. Spreading and falling law of conductive fiber cluster moving in the air [J].Journal of Ballistics， 2014(1): 35-39. (in Chinese)

(责任编辑：刘雨)

Study on Point Dispersing of Conductive Fiber Based on Exterior Ballistic Model

ZHANG Guang-hua， FENG Shun-shan

(School of Mechatronic Engineering， Beijing Institute of Technology，Beijing 100081, China)

An exterior ballistic model of the conductive fiber cluster, which includes stages from dispersing to falling to the ground，was presented to study on the point-dispersing law of the cluster. The model was based on dispersing exterior ballistic theory of submunitions and moving character of the fiber cluster. In particular, the influence of dispersion of dispersing velocities was considered. Besides, Monte Carlo method was applied to select the dispersing velocities to solve the model. Simulation results of spreading range and radius of the fiber clusters are consistent with the flight test, which proves the application reference value of the model.

conductive fiber; exterior ballistic; soft damage; fall point dispersion

2015-09-07

张广华(1987—)，男，博士生，E-mail:3120110144@bit.edu.cn.

冯顺山(1952—)，男，教授，博士生导师，E-mail:ssfeng@bit.edu.cn。

TJ 012.4

A

1001-0645(2016)12-1216-05

10.15918/j.tbit1001-0645.2016.12.002