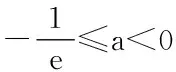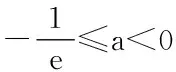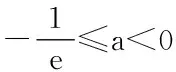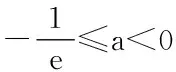一题多变赏析函数中的任意性与存在性问题

⌾王跃

(作者单位：安徽省宿州市灵璧县中学 234200)

一题多变赏析函数中的任意性与存在性问题

⌾王跃

函数中的任意性与存在性问题,也即函数中的恒成立与能成立问题,已成为高中数学考查的重点和难点,也是高考的热点题型。这类问题主要涉及到函数的最值和值域,常与导数相结合,并且与数形结合、分类讨论、转化与化归等数学思想紧密联系,综合性较强，也是一类易混淆、易出错的问题。因此,对此问题,笔者通过一题多变来研究函数中的任意性与存在性问题，并给出解决相关问题的方法归纳,供同仁在教学中参考,同时希望对复习备考的学生有所启示和帮助。

例:已知函数f(x)=x2-2x+2，g(x)=ax+lnx(a∈R),若存在x1∈[0,1]，x2∈[1,e]使得f(x1)

(1) 当a≥0时,由于g′(x)>0,所以

g(x)=ax+lnx在x∈[1,e]单调递增,故

[g(e)]max=ae+1。

根据[f(x)]min<[g(x)]max即10;

x∈[1,e]单调递增,[g(e)]max=ae+1<1与[f(x)]min<[g(x)]max矛盾。故a不存在;

(4) 当a≤-1时,g(x)=ax+lnx在

x∈[1,e]单调递减,所以[g(1)]max=a，根据[f(x)]min<[g(x)]max,所以a>1，又因为a≤-1,故a不存在;

综上所述:实数a的取值范围为(0,+∞)。

归纳:x1∈D,x2∈E,f(x1)

⟺[f(x)]min<[g(x)]max。

变式1：若对∀x1∈[0,1],∃x2∈[1,e]使f(x1)

解析：∀x1∈[0,1],∃x2∈[1,e]使f(x1)

与[f(x)]max<[g(x)]max矛盾,不符合题意，故a不存在;

(4)当a≤-1时，g(x)=ax+lnx在x∈[1,e]单调递减，所以 [g(1)]max=a，根据[f(x)]max<[g(x)]max，所以a>2，又因为a≤-1，故a不存在;

归纳:∀x1∈D∃x2∈E,f(x1)

⟺[f(x)]max<[g(x)]max。

变式2：若对∀x1∈[0,1]，∃x2∈[1,e]使f(x1)=g(x2)成立，求实数a的取值范围(其中e为自然对数的底数)

解：设f(x)的值域为集合A，g(x)的值域为集合B，对∀x1∈[0,1]，∃x2∈[1,e]使f(x1)=g(x2)⟺A⊆B。易知A=[1,2]。

(1) 当a≥0时，因为g(x)在x∈[1,e]单

归纳：∀x1∈D,∃x2∈E,f(x1)=g(x2)

⟺f(x)的值域⊆g(x)的值域。

变式3：若∃x1∈[0,1]，∃x2∈[1,e]使f(x1)=g(x2)成立，求实数a的取值范围(其中e为自然对数的底数)。

解：设f(x)的值域为集合A,g(x)的值域为集合B,对存在x1∈[0,1]，x2∈[1,e]使f(x1)=g(x2)⟺A∩B≠φ，易知A=[1,2]。

(4)当a≤-1时,g(x)=ax+lnx在x∈[1,e]单调递减,B=[a,ae+1],因为ae≤-e,所以ae+1≤1-e<0，故a不存在;

归纳:∃x1∈D,∃x2∈E,f(x1)=g(x2)

⟺f(x)的值域∩g(x)的值域≠φ。

变式4：若对∀x1∈[0,1]，∀x2∈[1,e]使f(x1)

解析:若对∀x1∈D,∀x2∈E使f(x1)

(1)当a≥0时,[g(x)]min=a,所以a>2;

(5)当a≤-1时,g(e)=ae+1<2,不符合题意;

综上所述:实数a的取值范围是(2,+∞)。

归纳:∀x1∈D,∀x2∈E,f(x1)

⟺[f(x)]max<[g(x)]min。

通过对上述例题进行一题多变可以看出,此类型题目中均含有两个函数,并且含有两个变量。由于这两个变量在各自区间上的取值具有任意性,因此,这类问题最终转化为函数值域或最值问题加以解决。

(作者单位：安徽省宿州市灵璧县中学 234200)