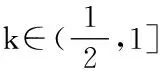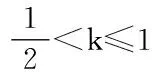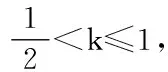用导数解决含参函数的最值问题
2016-02-21祝燕
⌾祝燕
(作者单位: 广东梅县东山中学514700 )
用导数解决含参函数的最值问题
⌾祝燕
以函数为载体,以导数为工具,考查函数性质及导数应用为目标,是最近几年函数与导数交汇试题的显著特点和命题趋向。解决导数在含参函数最值问题这类问题,主要是运用等价转化的数学思想,通过不断地转化,把不熟悉、不规范、复杂的问题转化为熟悉、规范甚至模式化、简单的问题。解决的主要途径是将含参数的函数的单调性弄明白。
题型一、函数含有参数,区间是确定的
(2014年安徽高考理科数学卷)设函数f(x)=1+(1+a)x-x2-x3,其中a>0.
(I)讨论f(x)在其定义域上的单调性;
∴f′(x)=-3(x-x1)(x-x2).
当x
(II)∵a>0,∴x1<0,x2>0.

∴f(x)在x=0和x=1处分别取得最小值和最大值.
当0 又f(0)=1,f(1)=a, ∴当0 当a=1时,f(x)在x=0处和x=1处同时取得最小值; 当1 题型二、函数确定,区间含有参数 已知函数f(x)=xlnx, 求f(x)在[t,t+1](t>0)上的最小值; 所以函数f(x)在[t,t+2]上递增,所以f(x)min=f(t)=tlnt; 题型三、函数、区间都含有参数 (2013年广东高考卷21题)设函数f(x)=(x-1)ex-kx2(k∈R) (1)当k=1时,求函数f(x)的单调区间; 试题解析:(1)k=1时f(x)=(x-1)ex-x2 ∴f′(x)=ex+(x-1)ex-2x=x(ex-2) 当x<0时ex-2<0,故f′(x)=x(ex-2)>0,f(x)单调递增; 0< x x>ln2时ex-2>0,故f′(x)=x(ex-2)>0,f(x)单调递增; 综上,f(x)的单调增区间为(-∞,0)和(ln2,+∞),单调减区间为(0,ln2). (2)f′(x)=ex+(x-1)ex-2kx=x(ex-2k) 由(1)可知f(x)的在(0,ln2k)上单调递减, ∴k-ln2k>0即k>ln2k ∴f(x)的在(0,ln2k)上单调递减,在(ln2k,k)上单调递增. ∴f(x)的在[0,k]上的最大值应在端点处取得.而f(0)=-1,f(k)=(k-1)ek-2k3 ∴当x=0时f(x)取最大值-1. 对于用导数解决含有参数的函数最值问题, 主要就是运用导数讨论出函数的单调性,画出函数的简单图像,不论是函数含有参数,还是区间含有参数,都要做到讨论的不重不漏,这样才能正确的求出函数的最值。 (作者单位: 广东梅县东山中学514700 )