红外搜索系统俯仰角测量的大气折射修正

祁蒙邱朝阳宋亚

（1华北光电技术研究所，北京 100015）

（2中航工业雷华电子技术研究所，无锡 214063）

红外搜索系统俯仰角测量的大气折射修正

祁蒙1邱朝阳2宋亚1

（1华北光电技术研究所，北京 100015）

（2中航工业雷华电子技术研究所，无锡 214063）

大气的非均匀分布导致光线在大气传播时产生折射现象，其传输路径变成一条曲线，影响红外搜索系统对空中目标的探测精度。要精确引导跟踪系统对目标进行锁定和瞄准，必须对目标的俯仰角度进行修正。通过研究波长、大气压强和大气温度对大气折射率的影响来定量描述大气折射率的变化规律，在大气球面分层模型中利用微分法推导测角误差，最终得出误差角度的计算方法。红外搜索系统在通过ADS-B技术进行标定之后，对高度500m的无人机和高度2km的飞机数据进行了验证，试验结果表明在低空红外探测系统中利用本方法可以有效提高测角精度。通过误差修正，提升了红外搜索系统的探测性能，使之在低空侦查、防御领域中能够发挥更为重要的作用。

大气折射 测角 误差修正 红外搜索

0 引言

搜索系统是以一定的规律对待搜索空域进行扫描，并对目标实施探测的系统。和雷达搜索系统一样，红外搜索系统主要针对低空、超低空远距离飞行器目标，对飞行器进行预警，给出目标方位和俯仰角度信息，并引导跟踪系统对目标进行锁定和瞄准。和雷达搜索系统相比，红外搜索系统具有隐蔽性好，不受电磁干扰，空间分辨率高，具有一定反隐身能力等优点，如今已成为低空防御系统中不可缺少的组成部分。

由于大气分布的不均匀，光线通过大气层传播时会发生折射现象，即被测目标到观测点的光线并非是一条直线，而是一条弯向地球的曲线[1]，红外搜索系统的测角数据会有很大误差，从而导致武器系统能够通过红外图像瞄准目标，却打不到目标的情况发生，所以对于俯仰角度进行误差修正很有必要。

大气折射率对于红外系统的影响，在工程上经常被忽略。之前相关文献对大气折射率的变化描述模糊[2]、对低俯仰角时的修正精度不高[3]，不能满足新型装备的使用要求。本文提出了一种测角精度的大气折射修正方法，通过定量描述大气折射率的变化规律，利用微分法推导测角误差，来有效修正误差。同时通过ADS-B计算角度真值的方法，选取500m高度的无人机和2km高度的飞机对地基红外搜索系统进行了实测数据验证。试验结果表明，实测数据和理论计算仿真具有很好的符合性。

1 大气折射率的变化规律

1.1 大气折射率

由于包围地球的大气时刻都在变化，大气的折射率也在时刻变化。大气折射率n不仅与光波的波长λ有关，而且也是温度T、水汽压e和压强p的函数。因为内陆地区空气相对干燥，水汽压对折射率的影响很小，故忽略相关项。在光学频率范围内，对流层中地球大气的折射率表示为[4]：

1.2 各个参数对折射率的影响

（1）波长对大气折射率的影响

在标准大气（T0=273.15K，p0=1.01325×105Pa）环境下，对波长范围 3.7～4.8μm，利用公式（1）计算得到大气折射率随波长的变化关系，如图1所示。可以看出，波长越长，大气折射率越小，整个红外中波波长范围内引起的折射率变化约为8×10–6数量级。因为空气折射率n近似为1，而n在10–6数量级变化，所以用n–1可以更为直观的显示折射率的变化规律。

图1 大气折射率与传输波长的关系Fig.1 Relationship between atmospheric refractive index and transmission wavelength

（2）大气压强对大气折射率的影响

取中波波长λ=4μm，温度T=273.15K，对于0～100kPa大气压强，利用式（1）计算得到大气折射率随压强的变化关系，如图2所示：大气压强越大，对应的大气折射率越大，且为正比关系。整个大气压强范围引起的折射度变化大约为3×10–4数量级。

图2 大气折射率与大气压强的关系Fig.2 Relationship between atmospheric refraction index and atmospheric pressure

（3）大气温度对大气折射率的影响

取中波波长λ=4μm，p=1.013 25×105Pa，对温度范围–60～40℃（213.15～313.15K），利用式（1）计算得到大气折射率随温度的变化关系，如图3所示：大气温度越高，对应大气折射率越小，成倒数关系，整个温度范围引起的折射率变化约为1.5×10–4数量级。

图3 大气折射率与大气温度的关系Fig.3 Relationship between atmospheric refractive index and atmospheric temperature

通过分析波长、大气压强和大气温度对折射率的影响可以看出：波长的影响最小，而压强和温度的影响都在10–4数量级，所以需要同时考虑这两方面的变化。

1.3 大气折射率的变化规律

对流层内的温度变化规律是等递减率，可表示为[5-6]：

式中 Tg为地面大气温度（K）；β≈–6.5℃/km，为高度温度变化率；h为离地面高度（km）。

对流层内的气压为：

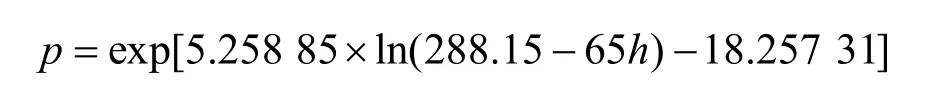
再综合式（1）～（2），可以得出大气折射率随高度变化得曲线，随着高度的增加，大气折射率逐渐变小，如图4所示。

图4 大气折射率与海拔高度的关系Fig.4 Relationship between atmospheric refractive index and altitude

2 俯仰角测量的误差分析及验证

对红外搜索系统的角度测量进行大气球面分层建模[7]。如图5所示，红外搜索系统在观测点C测得目标G的俯仰角度为d，目标的海拔高度为h，地球半径为R0，观测点到目标的地心夹角为φ。d角为大气折射后的观测值，而真实值为d0，所以产生一个误差角度Δd=d–d0。

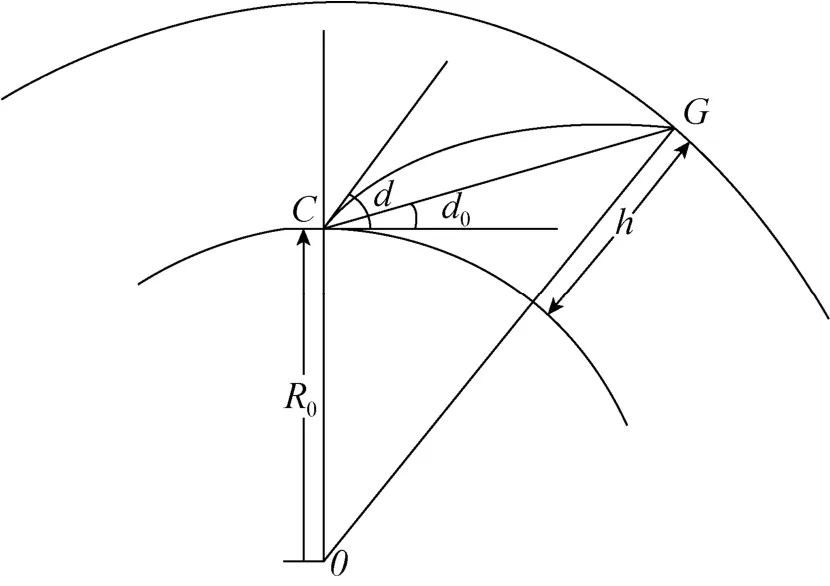
图5 红外搜索系统的俯仰角度测量Fig.5 Pitch angle measurement of infrared searching system

为推导方便，把φ微分成若干个小角dφ[8]，曲线CG可认为是若干直线的叠加，经过推导得到：

式中 n0为观测点地面大气折射率；n为海拔h高的目标点大气折射率。解出φ后通过三角关系可以推导出d0，最终求出Δd：

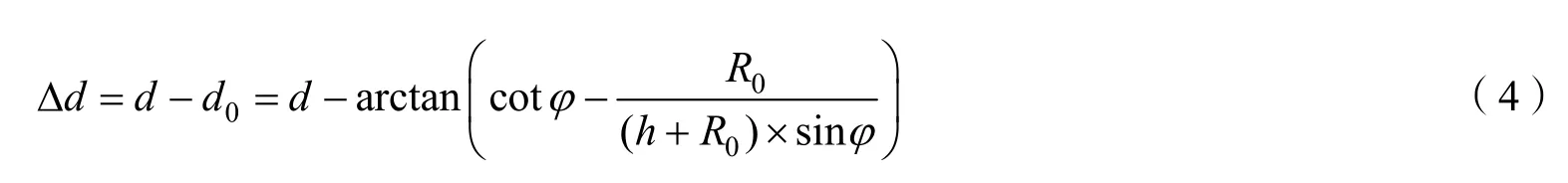
当目标在500m高度时，根据式（4）画出误差曲线，如图6所示，可以看出俯仰角越小，测角误差越大，最大能达到0.25°左右。俯仰角大于5°后，测角误差很小且变化缓慢。

图6 低俯仰角度测量下的测角误差Fig.6 Angle measurement error in low pitch angle measurement

在对红外搜索系统的角度测量进行工程验证之前，通常需要一种第三方测试的方法对红外搜索系统的时间空间坐标基准点进行标定，目前普遍采用的是差分GPS方法[9]：即把观测点和目标点的实时差分GPS信息当作真值，通过坐标变换求解两点之间连线角度，然后和红外搜索系统输出的测角信息进行比较，如果误差在一定范围之内，则标定正确。

传统的标定方法虽然比较成熟，但在工程实施上也有不足。包括：观测点和目标点的时间信息需要专门的设备进行时间同步，费时费力；数据整理工作复杂，计算周期长等。本文提出将ADS-B（Automatic Dependent Surveillance-Broadcast）技术应用于红外搜索系统的时空标定确认[10]，该方法不仅能实现0.01°的标定精度，而且操作简单、易于掌握。ADS-B自动相关监视技术本身是由国际民航组织推广，用于空中交通监视的技术手段。但随着该技术的普遍应用，研究人员发现地面接收设备如果将空中目标的实时ADS-B信息作为真值，通过坐标变换和雷达、光电设备测角信息进行比较，可大大简化设备的标定流程，系统标定原理如图7所示。

图7 利用ADS-B信息进行系统标定的步骤Fig.7 The procedure of system calibration using ADS-B

在使用ADS-B数据标定之后，通过一台地基红外搜索系统对该方法进行了实测数据的验证。目标选取了500m高度的无人机和2km高度的飞机，如图8所示。图中的实线为ADS-B真值，虚线为修正后的俯仰角度。

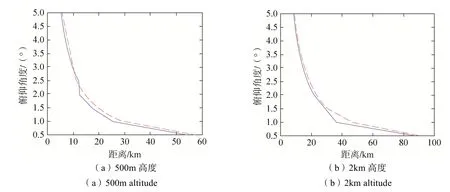
图8 真值和修正值的比较Fig.8 Comparison between true and corrected values

试验结果表明，实测数据和理论计算仿真具有很好的符合性，俯仰角度误差最大不超过0.1°。面对空中目标，尤其是低空目标，只有进行大气折射率修正，才有可能实现俯仰角测角精度优于0.1°的设计指标。

3 结束语

本文提出了一种低空红外搜索系统俯仰角测量的大气折射修正方法，通过研究大气折射率的变化规律，得出测角误差的计算公式，从而有效修正误差。该方法不仅适用于地基红外搜索系统，而且可以用于任何具有测角功能的红外探测系统，确保系统在测角精度方面的准确性。

References)

[1]宋正方. 应用大气光学基础[M]. 北京: 气象出版社, 1990: 7-10. SONG Zhengfang. Element of Application Atmosphere Optics[M]. Beijing: China Meteorological Press, 1990: 7-10.(in Chinese)

[2]金群锋. 大气折射率影响因素分析[D]. 杭州: 浙江大学, 2006: 8-17. JIN Qunfeng. Influence Factors on Atmospheric Refractive Index Analysis[D]. Hangzhou: Zhejinag University, 2006: 8-17.(in Chinese)

[3]钟声远. 激光对空中目标测距的大气修正研究[J]. 激光与红外, 2000, 30(4): 203-207. ZHONG Shengyuan. Study on Correction of Atmospheric Laser Ranging for Air Targets[J]. Laser & Infrared, 2000, 30(4): 203-207.(in Chinese)

[4]韩燕, 强希文, 冯建伟, 等. 大气折射率高度分布模型及其应用[J]. 红外与激光工程, 2009, 38(2): 267-271. HAN Yan, QIANG Xiwen, FENG Jianwei, et al. Height Distribution Profiles and Its Application of Atmosphere Refractive Index[J]. Infrared and Laser Engineering, 2009, 38(2): 267-271. (in Chinese)

[5]李双刚, 聂劲松. 大气折射对光电探测定位的影响[J]. 红外与激光工程, 2008, 37(增): 170-174. LI Shuanggang, NIE Jinsong. Effect of Atmospheric Refraction on Electro-optical Reconnaissance and Orientation[J].Infrared and Laser Engineering, 2008, 37(suppl): 170-174.(in Chinese)

[6]郗化, 李哲毓, 朱春燕. 大气折射修正的影响因素分析[J]. 价值工程, 2012, 31(22): 313-314. XI Hua, LI Zheyu, ZHU Chunyan. Analysis of Factors on Atmospheric Refractive Modifying[J]. Value Engineering, 2012, 31(22): 313-314.(in Chinese)

[7]刘兆军, 张智, 周峰, 等. 一种空间推扫型光学成像系统几何映射方法[J]. 航天返回与遥感, 2012, 33(1): 39-45. LIU Zhaojun, ZHANG Zhi, ZHOU Feng, et al. A Geomertrical Mapping Method for Space Push-broom Optical Imaging System[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(1): 39-45.(in Chinese)

[8]韩先平, 周慧. 低仰角大气折射的高精度修正方法研究[J]. 光电技术应用, 2008, 23(1): 24-26. HAN Xianping, ZHOU Hui. Study of High Accuracy Adjust Method of Atmospheric Refraction of Low Elevation[J]. Electro-Optic Technology Application, 2008, 23(1): 24-26.(in Chinese)

[9]左淑红, 左凤鸣, 郑丽娜. 相对差分GPS精度分析[J]. 测绘与空间地理信息, 2007, 30(2): 42-45. ZUO Shuhong, ZUO Fengming, ZHENG Lina. Precision Analysis of Relative Difference GPS[J]. Geomatics & Spatial Information Technology, 2007, 30(2): 42-45.(in Chinese)

[10]苑文亮, 唐小明, 朱洪伟, 等. 基于ADS-B数据的雷达标校新方法[J]. 舰船电子工程, 2010, 30(3): 147-150. YUAN Wenliang, TANG Xiaoming, ZHU Hongwei, et al. A New Method of Radar Calibration Based on ADS-B Data[J].Ship Electronic Engineering, 2010, 30(3): 147-150.(in Chinese)

[11]朱文越, 马晓珊, 饶瑞中. 大气光学湍流对光电探测器性能的影响[J]. 红外与激光工程, 2006, 35(3): 354-358. ZHU Wenyue, MA Xiaoshan, RAO Ruizhong. Optical Turbulence Effects on Electro-optical Sensors[J]. Infrared and Laser Engineering, 2006, 35(3): 354-358.(in Chinese)

[12]王祝和. 大气折射率随高度变化的初步探讨[J]. 大连海运学院学报, 1984, 10(2): 49-55. WANG Zhuhe. Preliminary Research on Changes of Atmospheric Refraction Index with Altitudes[J]. Journal of Dalian Marine College, 1984, 10(2): 49-55.(in Chinese)

[13]李华. 大气折射率误差对精密光电测距精度的影响研究[J]. 电光与控制, 2000, 78(1): 58-62. LI Hua. The Study on the Effect of Atmosphere Refraction Index Error on the Precise Optoelectronic Ranging Accuracy[J]. Electronics Optics & Control, 2000, 78(1): 58-62.(in Chinese)

[14]顾吉林. 典型天气大气辐射传输特性研究[D]. 大连: 大连海事大学, 2012. GU Jilin. Research of Atmosphere Radiative Transmission Characteristics for the Typical Weather[D]. Dalian: Dalin Maritime University, 2012.(in Chinese)

[15]任喜闯, 王江安, 吴荣华. 红外与微波波段大气折射率比较分析[J]. 舰船科学技术, 2011, 33(1): 65-68. REN Xichuang, WANG Jiangan, WU Ronghua. The Comparison of the Atmosphere Refractive Index of Infrared Band and Microwave Band Wave Lengths[J]. Ship Science and Technology, 2011, 33(1): 65-68.(in Chinese)

[16]闫雷兵, 张素君. 激光到达角误差修正方法研究[J]. 甘肃联合大学学报(自然科学版), 2010, 24(2): 52-54. YAN Leibing, ZHANG Sujun. Study on The Arriving Angle Error Correction Method of the Laser Transmitting[J]. Journal of Gansu Lianhe University(Natural Sciences), 2010, 24(2): 52-54.(in Chinese)

[17]任喜闯, 王江安, 吴荣华. 近海面光学与微波波段大气折射率结构常数比较分析[J]. 激光与红外, 2010, 40(8): 870-873. REN Xichuang, WANG Jiangan, WU Ronghua. Comparison of Refractive Index Structure Parameter for Optical and Micro Wave Band[J]. Laser & Infrared, 2010, 40(8): 870-873.(in Chinese)

[18]吴晓庆, 王英俭, 曾宗泳, 等. 一维大气边界层光学折射率结构常数的数值模式[J]. 强激光与离子束, 2002, 14(6): 819-822. WU Xiaoqing, WANG Yingjian, ZENG Zongyong, et al. Numerical Model of Atmospheric Optical Refractive Index Structure Parameter[J]. High Power Laser and Particle Beams, 2002, 14(6): 819-822.(in Chinese)

Error Correction of Pitch Angle Measurement on IR Searching System

QI Meng1QIU Chaoyang2SONG Ya1

（1 North China Research Institute of Electro-optics, Beijing 100015, China）
（2 AVIC Leihua Electronic Technology Research Institute, Wuxi 214063, China）

Due to non-uniform distribution of the atmosphere, the light is refracted in the atmospheric propagation and become a curve. It affect on air target detection accuracy on IR searching system. To accurately guide the tracking system to lock on to and aim at the target, the target pitch angle must be corrected. By studying the influence of wavelength, atmospheric pressure and atmospheric temperature, the variation of the atmospheric refractivity is quantitatively described. The differential method is used in spherically stratified atmosphere model to derive angle measurement error, and obtain calculation of error angle. After the calibration of ADS-B, some experiments are made with the UAV (500m high) and the aircraft (2km high). The results show that this method can improve the accuracy of angle measurement effectively. By error correction, detection performance of the IR searching system is improved and it can play a more important role in the low-level detection and defense.

atmospheric refraction; angle measurement; error correction; IR searching

TN215

A

1009-8518(2016)02-0051-07

10.3969/j.issn.1009-8518.2016.02.007

祁蒙，男，1977年出生，2003年获北京理工大学光学工程专业硕士学位，高级工程师。主要从事红外系统的研究。E-mail: Qimengqimeng@163.com。

（编辑：毛建杰）

2016-02-21

总装预研基金项目（14015130206106）