基于针孔阵列型的单次曝光双波长叠层成像*

罗 勇，许文慧，史祎诗,†

(1 中国科学院大学光电学院， 北京 100049； 2 中国科学院光电研究院，北京 100094) (2017年11月24日收稿； 2018年1月12日收修改稿)

叠层成像技术(ptychographic imaging engine, PIE)是由Faulkner 和Rodenburg提出的一种改进CDI成像的新方法[1-2]，快速发展应用于X-射线[3-4]与电子束成像[5-6]以及医学显微成像[7-8],光学信息加密[9-12]、攻击[13]等领域。传统PIE技术，增加系统参与成像的波长数量时，在成像分辨率、算法收敛速度、抗噪声能力等系统性能上都有一定程度的提升与增强，这一特性已应用于对三维物体的探测、物体形貌特征的测量、成像等领域[14-18]。尽管传统的多波长PIE成像技术，在成像质量、抗噪能力、算法收敛速度等方面具有明显的优势，但其仍然采用机械移动式的扫描方式，存在系统多次繁琐的曝光、数据采集时间过长，以及机械移动所导致的精度误差问题。相比而言SPI(single-shot ptychography imaging)单次曝光PIE成像技术，其采用单次曝光的方法实现多光束的交叠照明，较传统PIE技术有明显的优势[19-20]。

为克服机械移动或步进扫描的方法给多波长PIE技术带来的问题和缺陷，本文研究采用基于针孔阵列型的单次曝光双波长叠成成像技术方案，实现在双波长情况下单次曝光PIE成像，并完成光学成像实验，此系统相比传统多波长PIE成像,曝光次数成倍减少，缩短了实验数据的采集时间。同时还避免了传统多波长PIE成像系统，因增加波长数量而导致曝光扫描次数线性增加的劣势。在进行计算机模拟与实际的光学成像实验中，发现并指出相对传统多波长PIE成像系统，波长数量增加所带来的优势并不完全适用于针孔阵列型单次曝光的PIE技术，当在双波长或多波长情况下，如果选用激光波长λi不在其中心波长的一定范围内，或选取相邻波长间隔Δλ超出一定的系统相适应范围值时，随意增加照明光束，而不考虑其波长参数，系统的成像质量不会有提升，结果比单个波长的还要差，反之，进行一定的选取调整后成像质量、算法收敛次数等系统性能则会提升与增强。

1 原理分析

1.1 双波长单次曝光SPI原理

双波长单次曝光PIE原理示意图如图1所示，针孔阵列为一个N维的方形阵列，具体的尺寸可根据需求自由设计加工。该成像方法是基于针孔阵列实现对待测物体的多光束照明，一次性获得所有照明的交叠光束。基于针孔阵列的双波长单次曝光PIE系统，首先，由各自激光器出射的不同波长λi的平面波，传播经过N×N微型孔阵列后被分成N×N个照明光束。然后这些光束作为输入进入4f透镜成像系统，待测物体摆放于距离透镜Lens1的后焦面d位置处，光束在物体上发生交叠。最后在透镜Lens2的后焦面上，利用图像传感器CCD上采集得到含有物体信息的衍射强度图样。与传统的多波长PIE不同的是：此系统不再需要机械移动对物体进行多次曝光，照明光束直接经小孔阵列后分成N×N个光束，并在物体上发生交叠，完成所有的曝光程序；双波长单次曝光PIE，由于其是单次曝光所以图像数据采集的次数仅为2次，即为参与成像的波长数量，而传统双波长PIE的图像曝光次数，具体实验数据的采集次数则是2×N×N次,其中N×N代表扫描曝光的小孔数量一般有2×2=4,3×3=9,4×4=16，5×5=25,6×6=36,…,所以其采集次数多，效率很低，精度问题严重。

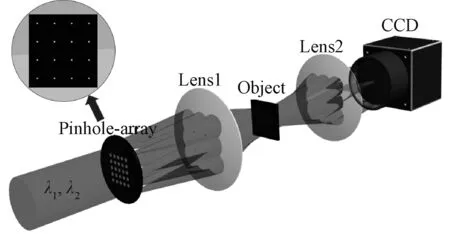
图1 基于针孔阵列的单次曝光双波长叠层成像原理Fig.1 Schematic of the principle of pinhole-array-based single-shot ptychography with dual-wavelength

假设系统参与成像的波长数量为Nλ,阵列数为Nn=n×n(n为横或列的步进数),NPIE、NSPI分别表示传统多波长叠层成像与针孔阵列多波长叠层成像各自的曝光次数，φ=NPIE/NSPI表示曝光次数的比值。则NPIE=Nλ×Nn，NSPI=Nλ，φ=NPIE/NSPI=Nn，所以减少到1/Nn，效率提高σ=(NPIE-NSPI)/NPIE×100%(结果见表1)。

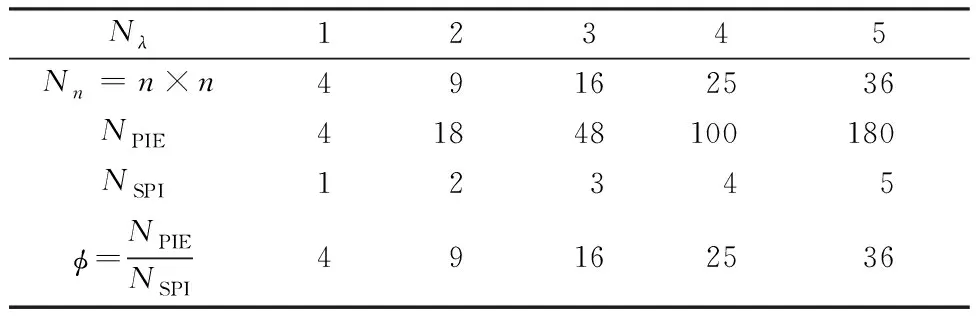
表1 传统PIE与SPI成像曝光次数的比较Table 1 Comparison of the exposure time between traditional PIE and SPI

1.2 算法简介及分析

单次曝光双波长SPI成像技术，与标准的多波长PIE成像系统的恢复重建算法相类似，且都满足近场衍射条件，在菲涅尔域内进行。本技术方案算法，具有预先对针孔阵列的衍射强度图分割，然后再进行菲涅尔变换运算的特点。

设透镜Lens1与Lens2的焦距为f1、f2，d0为待测物体距离Lens1后焦面的距离，符号ofrt与iofrt分别表示菲涅尔衍射变换和菲涅尔逆衍射变换，M为针孔阵列的小孔个数，其中M=1,2,…N×N，符号L和iL分别表示透镜正向因子与透镜逆向因子，设Rn为物函数，λi为参与成像的波长，其中i=1,2为波长标号[21-22]。

算法实施步骤如下：

步骤1将图像传感器CCD所采集得到的针孔阵列的强度信息图均匀地分割，符号∑M表示均匀分割运算，O0与Ow分别表示无样品时和有样品时在CCD面采集得到振幅(强度)图像信息

∑MO0，λi，f2)，

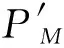
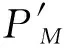
步骤2随机猜测物体为Rn，经针孔出射后的光束照明到物体上，衍射通过4f透镜系统，则有

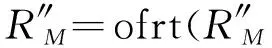
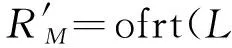
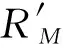
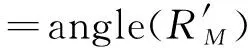
其中，angle表示取相位部分的处理。

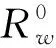
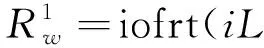
步骤5更新物函数

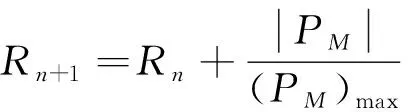
步骤6当所有记录的衍射光斑都迭代过一次之后，开始计算评价函数Co值，其中Co=cov{Rn，Rn+1},范围一般为[0～1]。当Co值越接近于1说明恢复重建的物体越接近真实的物体，越小说明恢复质量越差，偏离真实物体，成像效果越差。并以此判断选择迭代停止和迭代的次数。

2 实验及分析

2.1 双波长单次曝光叠层成像实验结果及分析

基于针孔阵列的单次曝光双波长SPI实验情况如下：采用两台相干性较好的半导体激光器，激光波长分别为λ1=470 nm，λ2=465 nm，在实验中适当调整激光功率使得其光斑亮度相同，针孔阵列规格为16孔(4×4)，物体摆放d0=22 mm,CCD像素大小为5.5 μm，透镜焦距f1=f2=75 mm，所使用的实验样品为分辨率版USAF 1951，在分辨率板中选取其中一部分数字“9”作为实验研究结果，最终对其进行复振幅的恢复重建，其中包含振幅部分和相位部分的分布。

进行复振幅恢复重建后，光学实验结果如图2所示，其中图2(a)为无样品时针孔阵列衍射强度图，2(b)为有样品时的针孔阵列衍射强度图，2(c)、2(d)分别为分辨率板上数字“9”复振幅恢复重建后的振幅与相位部分的分布。

本研究采用的方法，只需要进行2次数据采集，便能实现所有的曝光，完成全部实验数据的采集工作。在双波长、三波长甚至更多波长参与成像的情况下，基于针孔阵列型单次曝光PIE，具有实验操作简单，数据采集效率高与精度高的优势。

如果采用传统多波长PIE的实验方法，在相同的实验条件或环境下，对物体要进行4×4×2=32次的曝光，需完成32次的机械移动，必然存在精度误差和对系统稳定性的高要求，且数据采集效率低。

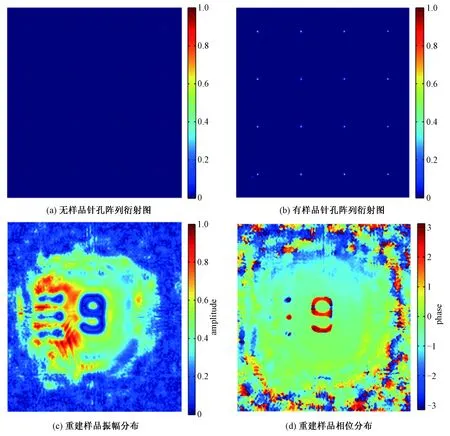
图2 双波长单次曝光叠层成像实验结果Fig.2 Experimental results of single-shot ptychography imaging with dual-wavelength

2.2 双波长针孔阵列型的单次曝光PIE波长参数的分析

PIE成像技术的本质是通过用局域(探针小孔)照明光场，对待测物体进行横向扫描并同时记录相应的衍射光斑序列,只要相邻两次照明区域间有一定比例的重叠, PIE 方法就能快速且可靠地重建出物体的相位和振幅分布。因而，重叠率(交叠量)无论对于何种形式及方案的PIE成像技术都显得尤为重要，当此交叠量无法达到一定比例时， PIE的各类成像系统都将失效。交叠率=重叠部分面积/相邻两次局域光场的面积，图3为PIE成像的交叠量，用公式Ω=S3/(S1+S2)×100%表示交叠率的运算式子，当交叠率Ω为0或者1时，叠层成像将演变为普通的相干衍射成像。相关研究结果表明交叠率是影响成像质量的关键因素, 当相对交叠区域增大到 50% 及以上时, 能获得高质量的复振幅, 但是随着交叠率的上升,恢复效率降低;交叠率的大小影响系统的成像质量和迭代算法的收敛速度[23-24]。

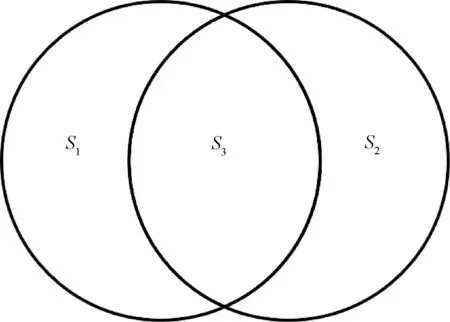
图3 PIE成像的交叠量Fig.3 Amount of overlap in PIE imaging

因此，在本文研究采用的针孔阵列型双波长单次曝光叠层成像技术方案中，由于采用不同波长的激光去照明物体，所导致的交叠区域变化的光路示意图，如图4所示。当采取不同波长λ1、λ2时，平行照明光束通过针孔阵列后达到第一个透镜Lens1，不同波长在中心轴上的交叠点不同，波长λ1、λ2分别对应dλ1和dλ2。因此，在物面上不同波长的激光光束照明产生的交叠面积及交叠率都发生很大的变化。

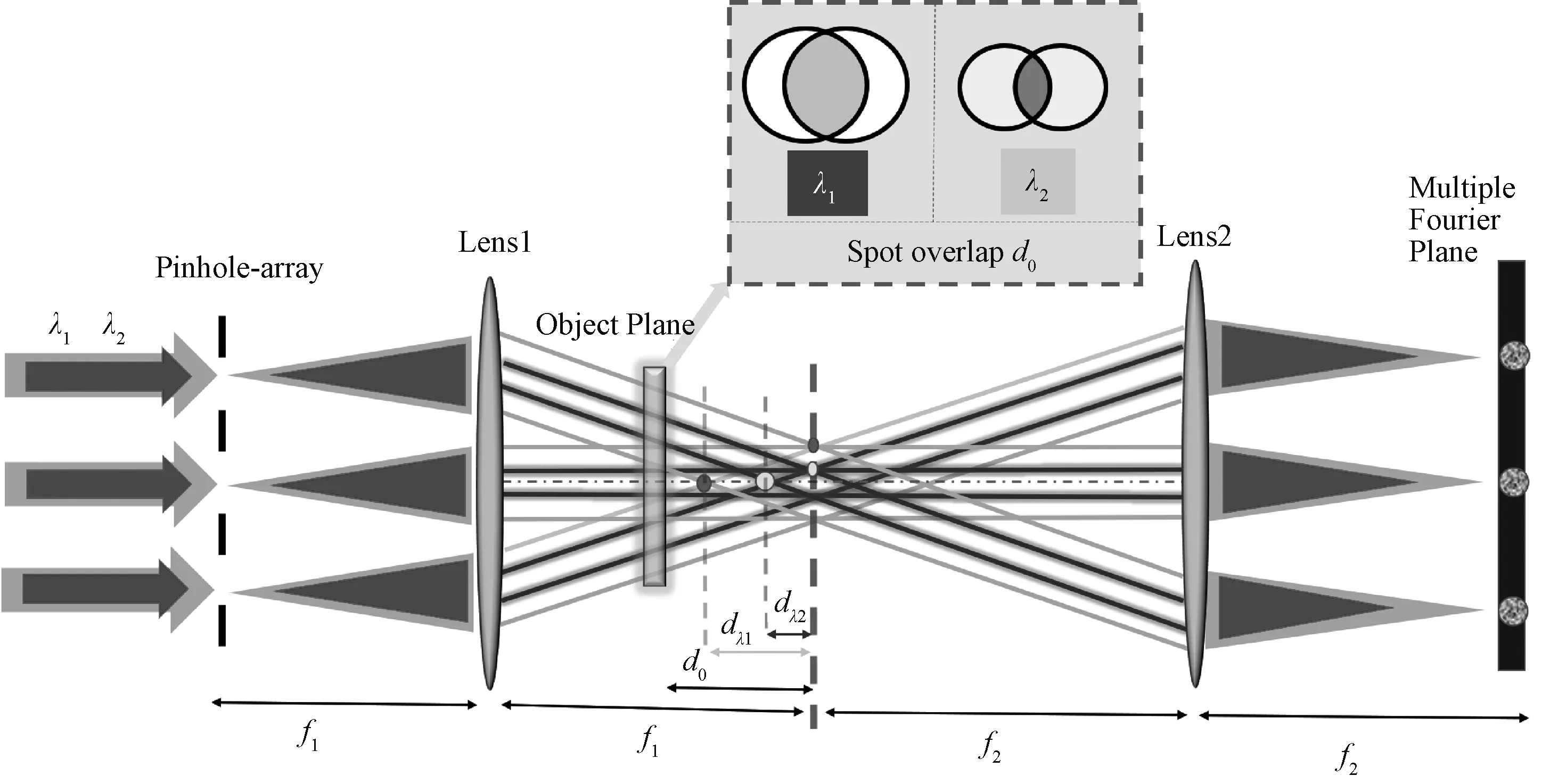
图4 交叠区域变化光路示意图Fig.4 Schematic of the optical path of the overlapping area change

然而，对于双波长孔径阵列型的单次曝光PIE，增加另一个波段的激光照明物体后，虽然通过移动待测物体的位置维持系统的交叠率不会发生较大变化，保证双波长情况下的系统平衡。但是，也因此引发了一系列如：系统抖动、系统稳定性、如何移动，以及移动多少、精度误差等问题需重新研究确定，另外改变系统的其他参数也同样存在可行性较低的问题。所以考虑从波长参数的选取上进行研究，得到有一定指导意义的结论。

波长参量变化只是纳米数量级的，因此相对于系统的各项距离参数来说都较小，所以如能选择适当的中心波长以及相应的波长间隔，使得因为参与成像波长的变化所导致系统交叠率失衡的缺陷得到一定范围内的平衡，从而保证成像质量。

2.3 成像系统中心波长及波长间隔的研究分析

为进一步论证和研究波长参数对本文系统的影响及作用，对中心波长和波长间隔进行计算机模拟分析。如图5所示，对本文的成像系统进行中心波长分析，在数值模拟的过程中所有迭代次数均设为120次，照明波长λi的取值范围为420～515 nm,波长间的步进值为Δ=5 nm，除波长变化外其他的系统参数均保持恒定不变。相关系数Co，取值范围为[0,1]。对于一般的成像系统而言，Co值是一个很重要且有价值的评价参数，在本文中选取Co=0.6作为系统的比较阈值，当Co值低于0.6时，判断为成像系统的成像质量不再满足要求。模拟实验所采用的样品为一个复振幅型的物体图像，这与实际的光学实验是相匹配的，振幅部分赋予为“Lena”和相位部分赋予为“monkey”，相位变化范围[-π,π]。

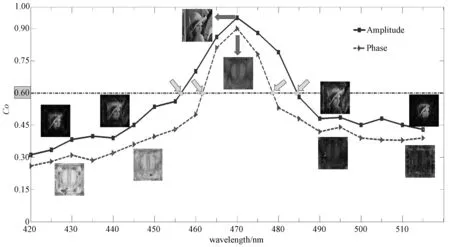
图5 中心波长的计算机模拟分析Fig.5 Computer simulation analysis of the center wavelength

模拟实验结果表明，从Co值曲线及恢复重建的灰度图像中可知：恢复重建样品的振幅与相位相关系数的Co，与波长λi变化值的呈倒“v”型字母的趋势，其中最为明显的是当波长λi处于460～480 nm时，Co值出现一个很高的峰值在470 nm处，而峰值两侧则是逐渐减小的趋势，当波长λi超出或不在460～480 nm之间时，Co值均小于0.6，并且偏离越远值就越小。此变化趋势一定程度上说明系统的成像波长在某一波长范围内成像质量较好，而不在或超出此波长范围，则系统的成像质量将受到影响或是变差。

对波长间隔的模拟分析，系统参数与进行中心波长的分析研究一致的。图6是本文成像系统中波长间隔的结果及分析，在数值模拟的过程中所有迭代次数均设为200次，坐标图中竖线选取迭代到达160次，以便于进行单波长与双波长的成像质量对比分析。基于针孔阵列型单次曝光叠层成像系统，模拟了样品恢复重建后的振幅和相位Co值变化关系。

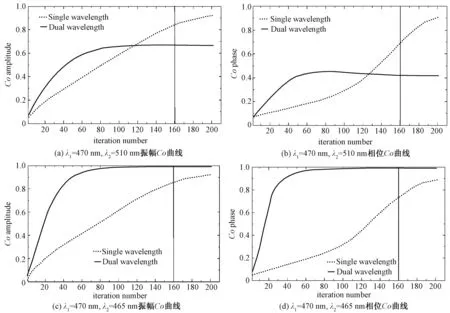
图6 波长间隔关系及结果比较分析Fig.6 Wavelength interval relationship and the comparative analysis results

图6(a),6(b)中所使用的波长λ1=470 nm，λ2=510 nm，计算波长间隔Δλ=λ1-λ2=470-510=40 nm，图中点线为单个波长参与成像，波长为λ1；实线为双波长，使用双波长参与成像，波长为λ1、λ2。图6(c),6(d)为在相同的条件下，使用波长λ1=470 nm，λ2=465 nm，波长间隔Δλ=λ1-λ2=470-465=5 nm时，点线为单个波长参与成像，波长为λ1；实线为双波长，使用双波长参与成像，波长为λ1、λ2。

研究及模拟实验结果表明，当使用波长λ1=470 nm，λ2=510 nm时，单波长情况下的振幅与相位Co值高于双波长的情况，说明此参数条件下的单波长成像质量比双波长好。然而当使用λ1=470 nm，λ2=465 nm时，双波长的振幅与相位Co值高于单波长，说明此参数条件下双波长成像质量比单波长好。数值模拟结果分析得知，使用不同波长间隔的照明光束(其他参数不改变的情况下)时，在相同的条件得到不同的实验结果及结论。

综上所述，本文研究使用的针孔阵列型单次曝光PIE技术方案，在进行双波长或多波长应用于测量、探测、成像时，中心波长及波长间隔成为影响系统性能及效果的重要因素。

3 结论

本文在传统双波长、多波长叠层成像的基础上，研究采用针孔阵列型的单次曝光叠层成像，实现在双波长情况下，单次曝光PIE。实际的光学实验和计算机模拟，论证了本研究采用的方案具有数据采集效率高、实验操作简单、系统稳定的优势，避免和克服了传统多波长叠层成像技术的缺陷及问题。同时还研究论证了，中心波长及波长间隔是影响系统成像质量及性能的重要因素。虽然系统的成像分辨率可能受到针孔阵列的设计精度及系统透镜的相差因素影响，但随着现代工艺技术的不断进步，这些因素的影响将会逐渐变小。因此，本文研究所采用的技术方案具有良好的应用前景及价值。