疲劳寿命预测频域方法分析与比较

林 明，谢里阳

(东北大学 机械工程与自动化学院，沈阳 110819)

疲劳寿命预测频域方法分析与比较

林 明，谢里阳

(东北大学 机械工程与自动化学院，沈阳 110819)

简单介绍了窄带分布法、Wirsching-Light法、Tovo-Benasciutti法和Dirlik法4种疲劳寿命预测频域方法。通过算例分析，在时域内采用雨流循环计数法，提取出各应力循环、均值和幅值，进行疲劳损伤累积计算，并以时域计算的损伤结果为基准，研究在不同不规则因子下，4种频域方法的适用性与准确性。结果表明，随机应力过程接近窄带随机过程时，W-L法能够较为准确地预测疲劳累积损伤结果；随着不规则因子的减小，应力随机历程更加接近于宽带随机过程，T-B法和Dirlik法更能准确地估计疲劳累积损伤。

功率谱密度；疲劳累积损伤；随机过程；频域分析

0 引言

工程实际中，对于机械结构及零部件疲劳寿命预测，有时域法和频域法两大类[1]。时域分析法首先采用载荷循环计数方法(目前一般采用“雨流循环计数法”)，从时间领域内的应力-时间历程中取出各应力循环及其幅值和均值，然后再进行疲劳损伤累积计算，最终预测零部件寿命。这种方法通常能得到比较准确的累积损伤分析精度，但缺点是需要足够长的时间来记录载荷信号历程，涉及较大的累积损伤计算工作量。

频域法是利用应力功率谱密度(PSD)来估测零部件疲劳寿命的方法。对于平稳各态历经随机过程，功率谱密度是描述其特性的关键参数。利用功率谱密度可以得到应力随机过程中各种应力的循环次数近似值。在疲劳寿命预测的频域法中，工程师时常会将结构简化为线性系统，通过频域分析，可以获得零部件危险部位的应力功率谱密度。对于一个具有复杂结构的有限元模型，对模型进行频域分析往往要比在时域中进行瞬态动力分析容易得多[2]，从而减少了工程中的计算时间与精力。

频域方法方便简单，因此得到许多国内外学者的认可，以及在工程中的应用。顾超林等[3]通过对某设备的弹簧片结构进行强度和疲劳寿命分析，详细地探讨随机振动疲劳仿真分析技术的流程及实现过程；王明珠等[4]针对缺口件提出了一种考虑应力集中和疲劳极限影响的缺口件频域随机振动疲劳寿命估算方法；曹明红等[5]设计了多组悬臂梁振动疲劳试验，将多种常用的宽带随机振动疲劳寿命频域预测方法进行了对比，由于其获得的试件危险点应力-时间历程具有明显的宽带过程特征，因此其结论更偏向讨论在宽带情况下的多种不同频域模型的准确性与适用性；朱涛等[6]针对于机车转向架，利用频域法对转向架构架进行了疲劳寿命研究，表明了频域疲劳计算方法有较高的疲劳寿命预测准确性，能够较好地预测随机振动下的疲劳寿命。D. Benasciutti等[7-8]提出了新的疲劳寿命预测频域方法，指出在宽带随机过程下，窄带分布法及其改善方法都会得出偏保守的结果，T-B法和Dirlik法优于其他频域方法，能够得到较为准确的计算结果；A. Nieslony等[9]对带孔棒状试件进行试验与仿真分析，研究了在多种不同曲线形式的功率谱密度下，4种频域寿命预测方法的合理性。

本研究考虑不同不规则因子下，即分别在窄带和宽带随机过程下，探讨各频域方法的适用性与准确性。鉴于时域分析法通常能得到较为准确的寿命预测结果，而频域方法的准确性更易受载荷历程特征的影响，本研究通过算例，以时域方法计算的结果为基准，分析对比多种频域模型在不同不规则因子下的准确性，为工程实际运用中选择合适的频域模型提供清晰的选用思路。

1 频域寿命预测方法

1.1 随机过程基础理论

随机过程按统计特性随时间变化情况，可以分为两类：平稳随机振动和非平稳随机振动。为了描述平稳过程随时间变化的特性，一般采用相关函数。而功率谱密度是在频域范围内描述平稳过程，是随机过程在频率域内的重要参数，它能够表达随机过程的能量分布情况。

理论上，自相关函数Rx(τ)和功率谱密度Sx(ω)符合维纳一辛钦定理，即

(1)

功率谱密度分为单边功率谱和双边功率谱。而在工程实际中频率ω>0，所以定义单边功率谱密度为：

统计矩是描述概率密度的数字特征，相似地，学者们引入谱矩，用来描述随机过程谱密度的数字特征。为了方便工程中的运算，根据ω=2πf，平稳过程X(t)的谱矩mi用单边谱密度G(f)定义为：

(2)

平稳过程根据功率谱密度的图形形状的不同，可分为两类：窄带平稳过程和宽带平稳过程。学者们通过引入不规则因子γ，来分辨平稳过程X(t)符合窄带过程还是宽带过程。

(3)

式中，mi为第i阶谱矩，其表达式见式(2)。

当不规则因子γ接近0时，平稳过程X(t)符合宽带随机过程。特殊地，当γ=0时，X(t)为白噪声过程；当不规则因子γ趋向于1时，平稳过程X(t)符合窄带随机过程。特殊地，当不规则因子γ=1时，X(t)为理想的窄带随机过程，即为含有单一频率的简谐波。

工程中还引入带宽系数ε，用于描述随机过程的带宽，用谱矩定义为：

(4)

其取值范围0≤ε≤1。当ε值趋于1时，随机过程对应宽带随机过程；当带宽系数ε值趋于0时，随机过程符合窄带随机过程。若已知一个高斯随机过程，根据其功率谱密度，可以求得单位时间内的峰值期望率Vp。同样的，亦可以求出单位时间内的正斜率穿越期望值V+。

(5)

1.2 频域疲劳寿命计算模型

1)窄带分布法。

Bendat等[10]首先提出了一种利用PSD估算疲劳寿命的方法。他提出：随着带宽的减小，随机信号的峰值概率密度函数会趋向瑞利分布。另外，针对一个窄带随机信号，Bendat假定对应于全部的正值波峰，必定有相等数值的波谷与其对应。根据这个假设，应力幅值S概率密度函数会趋于瑞利分布，其表达式为：

(6)

式中，σ是应力随机过程的均方根，其表达式为：

(7)

根据Miner线性累积损伤理论，结构的疲劳损伤为：

(8)

式中：ni表示第i级应力水平下的实际应力循环次数；Ni表示应力幅值为Si时S-N曲线下对应的寿命循环值。如果应力状态符合连续分布，则在时间T内，应力处在范围(Si，Si+ΔSi)内的应力循环次数为

(9)

式中，p(S)为应力幅值的概率密度函数，v为单位时间内的应力循环次数。

联立式(8)、式(9)可得到连续分布应力状态下时间T内的疲劳损伤D。

(10)

通常情况下，工程中用疲劳寿命曲线来描述材料的疲劳性能。其幂函数公式为：

(11)

式中，m、C为材料常数。

在窄带信号中，单位时间内应力循环次数V等于均值正穿越率V+(在窄带过程中，V+与Vp也相等)，结合式(6)、式(10)和式(11)，得到窄带过程下疲劳损伤结果为

(12)

令D=1，则得到构件发生破坏的寿命时间T为

(13)

2)Wirsching-Light法。

对于宽带过程，由于Vp、V+数值相差较大，采用窄带分布法估计的寿命比实际寿命小很多，因此针对宽带随机过程，需要对公式进行修正。P H Wirsching等[11]根据不同PSD形状进行修正，获得了适用于宽带随机振动的寿命估算公式：

(14)

式中，λ为修正因子。修正因子、材料参数和不规则因子γ满足

λ=0.926-0.033m+(0.074+

(15)

3)Tovo-Benasciutti法。

Benasciutti和Tovo[7-8]也提出了基于窄带模型的修正方法，他们提出的雨流幅值概率密度函数如式(16)所示。

(16)

式中：γ为不规则因子,参数b表达式为

(17)

式中α1、α2满足

(18)

联立式(10)、式(11)和式(16)可算得疲劳累积损伤结果。

4)Dirlik雨流幅值分布模型。

Dirlik通过Monte Carlo技术时域模拟[12]，研究了70种不同形状的功率谱密度函数，最后用1个经验表达式去估计雨流循环幅值的概率密度函数。他研究表明，雨流循环幅值能用2个瑞利分布和1个指数分布的组合来表达，经验表达式为：

(19)

式中：

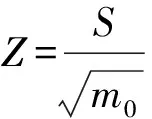
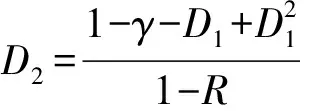
联立式(10)、式(11)和式(19)可算得疲劳累积损伤结果。

2 算例分析

采用1个含中心孔的LY12-CZ板[13]为算例分析样品(图1)。板的宽度W=50 mm，孔直径D=8 mm，加载方式为拉伸。查得LY12-CZ铝合金板的σb=407 MPa、σs=270 MPa。

图1 中心孔板

根据中心孔板板宽W和孔直径D，查阅资料可得KT=2.6。查得在KT=2.6，平均应力σm=0下的S-N曲线，S，N值如表1所示。

表1 KT=2.6 时的S、N值

根据表1数据，可求出零件的S-N幂函数的表达式中C=3.105 659×1017，m=6.093 845。

通过计算，得到不同模型的累积损伤结果，并与时域方法计算的累积损伤进行比较，如表2所示。

表2 时域与频域疲劳累积损伤结果对比

从表2中可以看出：

1)针对于本例，可以看出频域方法计算的疲劳累积损伤比时域方法计算得到的结果偏大，即频域方法比时域方法偏于保守；

2)在较高的不规则因子γ下，应力随机过程接近窄带随机过程，W-L法计算的结果最为接近时域方法计算得到的疲劳累计损伤结果，相对误差为41.81%；在较低的不规则因子下，W-L法计算的结果过于保守，误差偏大，而T-Be法和Dirlik法计算的结果更接近时域方法计算的疲劳累积损伤结果，相对误差分别为26.88%、23.66%。这与文献[7-8]中的结论“在宽带随机过程下，窄带分布法及其改善方法都会得出偏保守的结果，T-B法和Dirlik法优于其他频域方法，能够得到较为准确的计算结果”比较符合。

3 结论

1)通过与时域疲劳预测方法的对比，研究了在不同不规则因子下，多种频域疲劳预测方法的适用性。随机应力历程接近窄带随机过程时，W-L法能够较为准确地预测疲劳累积损伤结果。

2)随着不规则因子的减小，应力随机历程越接近宽带随机过程，T-B法和Dirlik法更能准确地估计疲劳累积损伤。

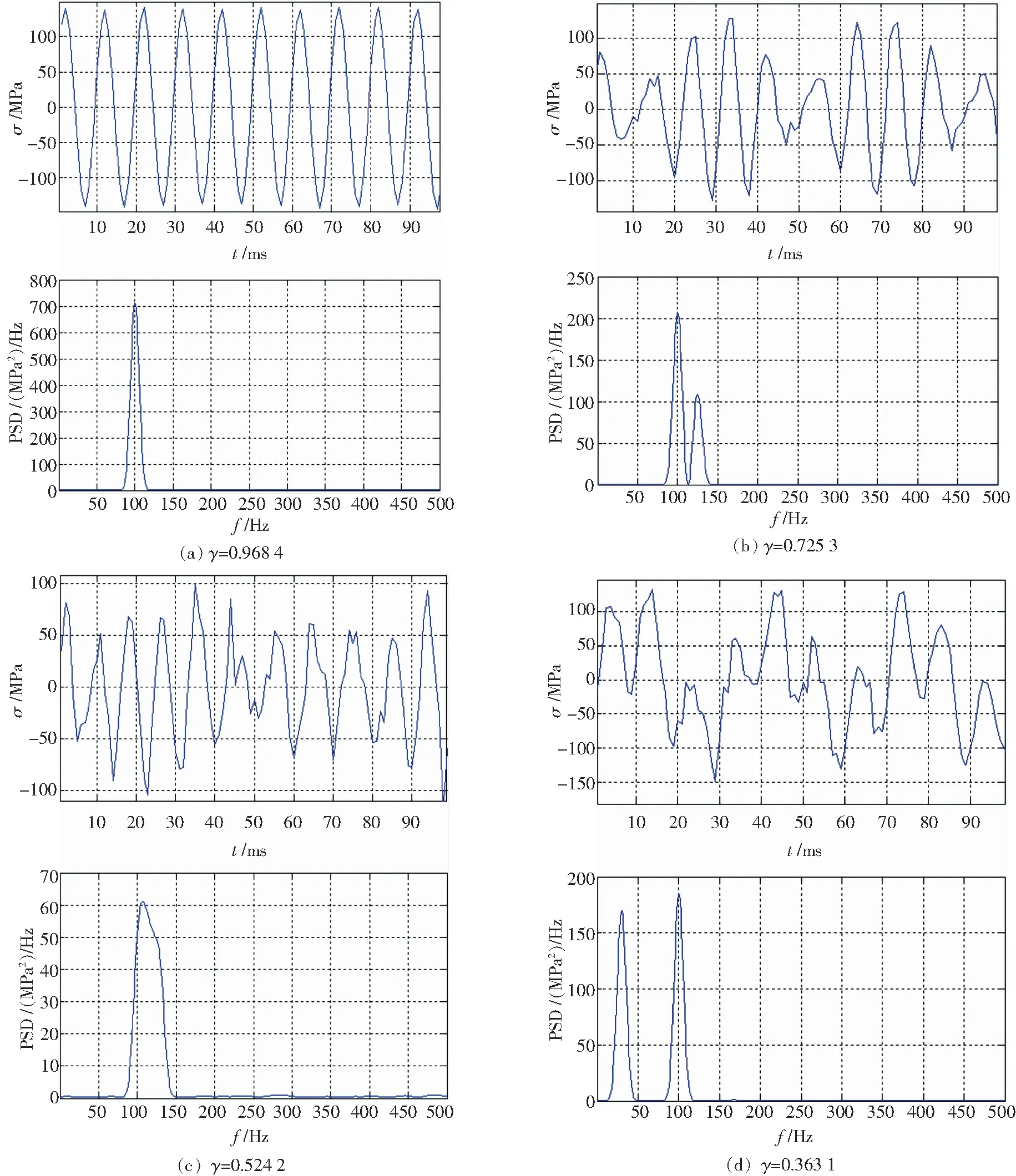
图2 应力历程与功率谱密度

[1] Halfpenny A. 基于功率谱密度信号的疲劳寿命估计[J]. 中国机械工程,1998,9(11):20-23.

[2] 刘建树. 高速列车转向架构架频域疲劳寿命研究[D]. 成都:西南交通大学,2011:2-13.

[3] 顾超林,王轲. 基于功率谱密度的结构随机疲劳寿命仿真[J]. 计算机与现代化,2010(2):143-146.

[4] 王明珠,姚卫星. 随机振动载荷下缺口件疲劳寿命分析的频域法[J]. 南京航空航天大学学报,2008,40(4):489-492.

[5] 曹明红,邵闯,齐丕骞. 宽带随机振动疲劳寿命的频域分析与试验对比研究[J]. 机械科学与技术,2013,32(6):839-844.

[6] 朱涛,肖守讷,阳光武,等. 基于频域法的转向架构架疲劳寿命研究[J]. 机械强度,2016,38(1):160-166.

[7] Benasciutti D, Tovo R. Spectral methods for lifetime prediction under wide-band stationary random processes[J]. International Journal of Fatigue,2005,27(8):867-877.

[8] Benasciutti D, Tovo R. Comparison of spectral methods for fatigue analysis of broad-band Gaussian random processes[J]. Probabilistic Engineering Mechanics,2006,21(4):287-299.

[10] Bendat J S, Piersol A G. Measurement and analysis of random data[J]. Technometrics,1968,10(4):869-871.

[11] Wirsching P H, Shehata A M, Wirsching P H, et al. Fatigue under wide band random stresses using the rain-flow method[J]. Journal of Engineering Materials & Technology,1980,106(7):1593-1607.

[12] Dirlik T. Application of Computers in Fatigue Analysis[D]. UK:University of Warwick,1985:47-132.

[13] 姚卫星. 结构疲劳寿命分析[M]. 北京:国防工业出版社,2003:95-99.

Analysis and Comparison of Frequency-domain Approaches of Fatigue Life Prediction

LIN Ming，XIE Li-yang

(SchoolofMechanicalEngineeringandAutomation,NortheasternUniversity,Shenyang110819,China)

This paper provides a brief review of several frequency-domain approaches of fatigue life prediction, specifically the narrow-band approximation, Wirsching-Light, Tovo-Benasciutti and Dirlilk models. By using sample calculation, this paper adopts rain-flow cycle counting method within the time-domain to obtain the stress cycles as well as their mean value and amplitude, which can be used to evaluate the accumulated fatigue damage. Then based on the results of fatigue cumulative damage of time-domain calculation, this paper detects the applicability and accuracy of the four frequency-domain approaches under different irregular factors. The results show that when stochastic stress process gets close to narrow-band random process, W-L method can predict the fatigue cumulative damage results more accurately. And with the decrease of the irregular factors, stochastic stress process gets closer to wide-band random process, and thus T-B method and Dirlik method can estimate the fatigue cumulative damage results more accurately.

power spectral density; fatigue cumulative damage；random process; frequency domain analysis

2016年7月18日

2016年9月20日

国家自然科学基金(51335003)

林明(1991年-)，男，硕士研究生，主要从事结构疲劳寿命预测等方面的研究。

TH122

A

10.3969/j.issn.1673-6214.2016.05.001

1673-6214(2016)05-0265-05