借助几何直观 突破教学难点——以“分数乘除法”的教学为例

□吴慧婷

借助几何直观 突破教学难点
——以“分数乘除法”的教学为例

□吴慧婷

计算教学是数与代数领域重要的基础内容。算理的理解是计算教学中公认的难点。就计算教学而言，可以采取用图示贯穿整个教学，用图形表征问题等方式发挥几何直观的价值。通过直观助力，让学生经历思、画、析、辨、算和悟，既可以对相关难点进行有效突破，也能进一步培养学生几何直观的意识和能力，从而提升几何直观素养。

算理算法 几何直观

分数乘、除法是人教版六年级上册的学习内容，是小学教学中一个公认的难点。如：分数乘法的意义，学生难拓展；分数乘除法的算理，学生讲不清；解决问题，为什么这样解答学生道不明。最终原因是缺乏图和式的对照，重视算法弱化算理，更忽视数学思想的渗透。现行教材已对原实验教材进行改编。原实验教材将分数乘除法分两个单元编排，现在人教版教材分拆成分数乘法、分数除法、比三个单元，并将倒数的认识移至分数除法单元。

根据现在教材的编排特点，学生的学情，教学中的困难，笔者将图示贯穿于整个单元，借助几何直观开展分数乘除法两个单元的教学，以形助数，知意义、明算理、清关系，数学学习变得简单明了。

一、画中迁移，呈现结构化的直观

分数是在整数、小数的基础上教学的。分数加、减法的意义，与整数加、减法的意义一致。

分数乘法的意义较复杂，第一种表示求几个相同加数的和，第二种表示一个数的几分之几是多少。分数乘法第二种意义的理解是难点，要在整数的基础上拓展。因此，在教学分数乘法的意义时，试着用画图的方式，用图示来沟通分数乘法与整数乘法的关系。

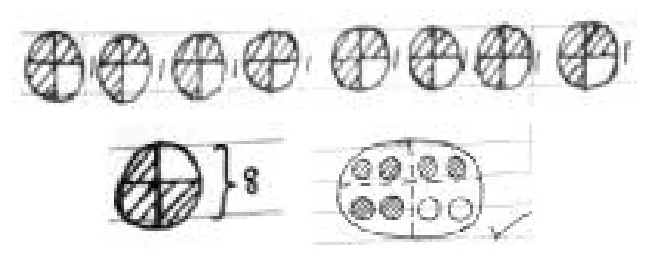
学生已有丰富的学习经验，知道乘法表示求几个相同加数的和的简便运算，学生正确画出8个相加的图示，和整数乘法相同。学生将8个圆平均分成4份，取其中的3份，或者将一个圆看作8，也平均分成4份，取其中的3份，两种图示都正确地表示了个8是多少，也就是8的是多少，只是表达方式不同而已，表示8的的教学难点就解决了。学生画图，知识迁移，把分数乘法的意义与整数乘法的意义统一，知识融会贯通，对分数乘法的另一种含义的理解水到渠成。

二、画中比较 ，呈现最优化的直观

理解算理掌握方法是计算教学的本质。小学高年级学生需要几何直观的支持进行逻辑思维和运算。平时教学中，常见师生对分数乘除法的计算方法重概括，技能重训练，但让学生说说为什么这样计算时，学生对算理的理解并不深刻，只会记法则。因此，教学分数乘法算理时，让学生尝试用画图的方式来理解算理，同时掌握算法。如六年级上册第3页例3，李伯伯家有一块公顷的地。种土豆的面积占这块地的。种土豆的面积是多少公顷？，用画图来表示。学生典型作业如下：

学生的学习是将一个个冲突进行化解和发展的过程。从图示可知，，意义算理算法三合一。学生画图，找到1公顷长方形地的，即公顷，再将其中的公顷平均分成5份，取1份。学生在比较与思辨中，认为五幅图都正确，但上面三幅图只从一个维度表示，不能清晰地看出这一份与整块地的关系，也就是2、5、10的关系不明显。于是学生更关注下面两幅图，从横、列两个维度表示，可以先竖着平均分再横着平均分，反之也可以。画图是学生表征问题的过程，学生感知到把其中的公顷平均分成5份取1份，相当于把整块地平均分成10份取1份。，用2×5作分母，1×1作分子，知其所以然。

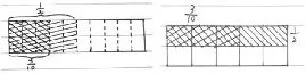
图1

三、画中递进，呈现有层次的直观

除以一个数，等于乘这个数的倒数。为什么呢？对于其中的道理，许多学生道不明，甚至有教师也说不清。因此，要突破分数除法算理这一难点，从分数除以整数（整数从偶数到奇数）到分数除以分数，层层递进，借助画图来明理。

用画图来表示结果。学生典型作业如下：

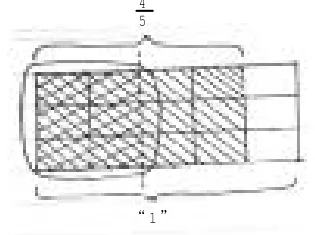
图2

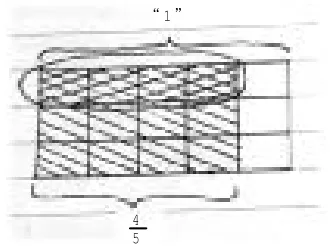
图3

图4

学生的学习能力和水平是有差异的，表现出不同的思维特点。如，计算方法多样化，有一半学生不画图直接用小数算，0.8÷2=0.4。少数学生画图时，将5份中的4份平均分成2份，每份是（图2）。其余学生将分数乘法的画图经验用到分数除法中，画成的是多少（图3）。，分子4÷ 3不能整除，0.8÷3商是无限小数，只能转化为求的是多少（图4），从一般到特殊。与÷2类同，学生又根据数的特点灵活选用两种不同方法。学生从不同角度思考问题，层层递进，将个性化的方法和普通方法建立联系。分数除以整数的算理是建立在平均分、分数的意义、求一个数的几分之几是多少三个知识点的基础上进行推理，突出逻辑推演的特点。

分数除法的算理算法是小学阶段最难的知识点，为什么要乘除数的倒数呢？如何内化为学生的认知呢？将难点放大，从两个层次说理，一是整数除以分数，重点突破1里面有几个，2÷2×3=，此时的关键处在直观的基础上初步建立推理过程；二是延伸到分数除以分数，，在变式中巩固。由浅入深，由特殊到一般，画图，想图，析图，说理，知识迁移，在递进中经历分数除法算理算法的构建过程，培养学的推理能力。

四、画中明意，呈现有留白的直观

在小学阶段，学生最难以理解和掌握的是用分数乘、除法解决问题。在教学中，常听到学生熟练地背着：如果告诉单位“1”的量，求单位“1”的几分之几用乘法；如果告诉具体的量及对应的分率，求单位“1”的量用除法。当遇到用分数乘除法解决问题时，学生还是盲目猜题。其实，分数乘、除法意义的理解是正确分析、解答分数乘除法问题的前提。教学中将分数乘除法计算教学的图示进行改编，采用线段图，呈现留白的直观，可进行数形转换的思维训练策略。

分数乘、除法解决问题，题意抽象难理解，学生缺乏分析的能力。线段图表示题意，容易找到数量关系，特别适用于从正向思维到逆向思维的转换。根据不完整的直观图，学生补信息，呈现了完整的六幅图示六个问题，从正向思维到逆向思维，从一步计算到两步计算，自觉建立了分数乘、除法解决问题的知识体系。六幅图示，具体的量与分率的对应关系清晰，等量关系明了，就能正确、灵活地解决问题。用分数乘、除法解决问题，要在整体中学，采用横向、纵向比较，意、图、式结合，数形转换，将抽象的数学问题直观化、生动化，变抽象思维为形象思维，突出数学问题的本质。

图5

分数乘除法单元教学实践的启示：在计算教学中，充分利用直观示意图，将图形与数学算理紧密结合，能将抽象的算理形象地显现出来，为算法的建构提供原型支撑。算式和图形完全有机地对应与转化，对学生理解算理，构建创造性的算法具有重要的意义。

学习数学要突出知识的本质，让学生在已有的知识和经验中建构新的知识。学生要主动经历认知冲突发生、发展与化解的过程，学会用几何直观帮助学习，在画图、说图、析图、比图、想图中学会推理，学会概括，学会学习，发展学生的思维能力，提高学生的数学素养。

（浙江省长兴县第二实验小学 313100）