“思过留痕”：学生数学思维生长的推进器

□席爱勇

“思过留痕”：学生数学思维生长的推进器

□席爱勇

让学生在数学学习中“思过留痕”，可以促进学生数学思维有条理、更全面、更灵活、更深刻、系统化和可持续发展。“思过留痕”可以成为学生数学思维生长的推进器，它既是一种提升学生数学思维品质的有效资源，也是教师读懂学生进行因材施教的有效策略。

思过留痕 思维生长

俗话说：“人过留名，雁过留声。”在数学学习中，教师是否可以让学生的数学思维“思过留痕”呢？即让学生在数学课堂教学或作业时，把自己的思维过程和方法用文字、符号或图表表示出来，留下痕迹。这样既便于学生自我反思、自我完善、自我评价和自我提升，也便于学生与他人交流共享、思维碰撞、相互借鉴和取长补短，更便于教师及时了解学生、读懂学生、研究学生的数学思维，及时采取有效措施进行有针对性的教学。实践证明，“思过留痕”是学生数学思维生长的推进器，是提升学生数学思维品质的有效策略，也是教师读懂学生进行因材施教的有效策略。

一、思过留痕，让数学思维有条理

思过留痕，可以让学生清晰地看到：对于一个数学问题，自己或他人先是怎么想的、怎么做的，后又是怎么想的、怎么做的，使数学思维过程清晰可见，条理分明。

二年级学生认识钟面上的时刻是一个难点，很容易认错。如写出右图钟面上的时刻，学生就会出现如下一些错误结果：1：11、2：11、2：55、11：02、11：10。究其原因，11：02、11：10是没分清时针和分针导致的错误，而1：11、2：11、2:55则是没弄懂时针和分针行走的规律导致的错误。仔细分析这些错误，让学生写出如右图的思考过程：先找钟面上较短的时针，指在1和2之间，是1时多；再找钟面上较长的分针，指向11，因为分针走1大格是5分钟，所以用11×5=55分，因此，钟面上的时刻是1：55。学生像这样进行数学思维，并写下主要思维过程，就会自己发现和避免上面出现的各种错误。

教师引导学生有条理分步骤地进行数学思维，一方面可以大大降低学生的认知负荷，弥补“想了这个忘了那个”的低年级学生思维普遍存在的不足，更重要的是可以帮助学生养成有条理、逐步思考问题的好习惯，不断提升数学思维水平。

二、思过留痕，让数学思维更全面

低年级学生很容易出现将图形数多了或数少了的现象，怎样让他们不重复不遗漏地数出图形的个数呢？有顺序一一列举是一个非常有效的方法。

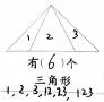
如下图，要数出图中一共有多少个三角形，可以让学生先在图上标出1、2、3（如左图），再有顺序地一一列举出来：1，2，3，12，23，123，就很容易数出一共有6个三角形。教师引导学生把图形按编号先一一列举出来再数一数，就不容易重复或遗漏了。

三、思过留痕，让数学思维更灵活

教师让学生把自己数学思维的角度、过程、方法写下来再进行交流，这样就可以相互学习、相互借鉴、取长补短，使数学思维变得更加灵活和开阔。

如笔者在执教苏教版小学数学六年级上册“解决问题的策略”例1时（如下图），放手让学生列式解答，有的学生用分数的思想列式解答，有的学生用按比例分配的思想列式解答，还有的学生用方程的思想列式解答。笔者让他们分别把自己的解法写出来，同学之间相互交流研讨，相互理解别人的解题思路和思维方法，从而相互启发，不断促进数学思维灵活性的发展。

四、思过留痕，让数学思维更深刻

思过留痕，可以让学生把数学思维过程和方法显示出来，便于后续学习可以借鉴。

例如，学完“加法交换律”后，笔者让学生总结回顾本课所经历的数学思维过程，学生总结如下：

在学习“加法结合律”时，笔者首先让学生全面回顾学习“加法交换律”所经历的数学思维过程，让学生按照上面的思维过程尝试探究加法结合律，大部分学生都能顺利探究出加法结合律：（a+b）+c=a+（b+c）,并进行广泛应用，解决实际问题，还进行了大胆类比联想：减法、乘法、除法是否也有类似的规律呢？学生一旦掌握了这样科学探究的思维过程和方法，数学学习就会变得非常轻松高效。学生可以用这样的思维过程和方法学习“乘法交换律”“乘法结合律”和“乘法分配律”，在多次经历科学探究的数学思维过程以后，学生遇到类似规律的学习就会自然运用，形成科学的数学思维习惯。

五、思过留痕，让数学思维系统化

思过留痕，需要学生将数学思维进行不断梳理，不断加工，连点成线，连线成面，连面成体。在这个过程中，学生的数学思维逐步从零散走向联系，从碎片走向系统，从而打通数学知识的内在联系，实现系统化建构，便于他们在以后相关数学学习和生活实践中灵活提取和综合应用。

例如，学生学完“三角形”以后，笔者引导他们作如下图的梳理：

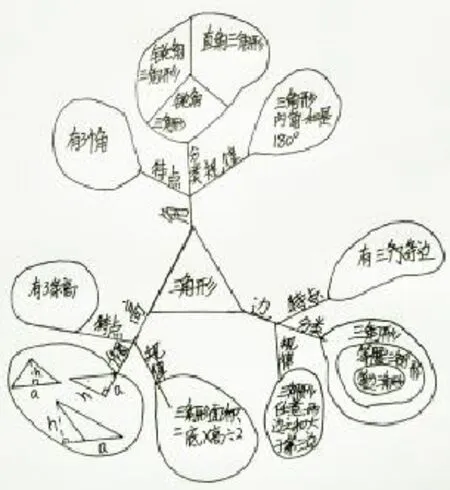
从上图可以清晰看出，学生从三角形的角、边、高三个纬度出发，每一个纬度又可分成“特点、规律、分类、作图”等多个方面，多维度、网络化、立体式建构三角形的知识结构体系。学生以后再学习三角形的相关知识（如初中学习全等三角形和相似三角形、三角函数等）也会自然从这些纬度进行数学思维，不断充实完善三角形的知识结构体系。同时，学生在遇到三角形方面的实际问题时，也会自然从这些纬度灵活提取相关数学知识，综合运用相关数学知识分析解决实际问题。可见，上图不仅仅是三角形知识结构的全面整理，更是学生对三角形全面再认识的数学思维的系统整理。

思过留痕，促进学生不断梳理自己的数学思维，将内隐的难以言传的数学思维过程和方法个性化地呈现出来进行展示交流，在展示交流中相互碰撞，不断优化，不断完善，不断走向全面系统和深刻。

六、思过留痕，让数学思维可持续

让学生把数学思维过程、方法、策略充分暴露展示，这样可以促进他们自觉主动地进行自我反思，实现数学思维纠偏纠错、自我矫正、自我完善和自我提升，从而促进数学思维的可持续发展。

例如，二年级学生在确定方向时经常出错，笔者以为是学生没有找准方向，便让学生在图中先按照“上北下南，左西右东”标出“东、南、西、北”四个方向后再确定，但是在数学作业中错误率还是比较高。经过访谈调查才发现，有一些学生找不到观察点，不知道从哪里看向哪里。于是笔者让他们根据题目要求圈出观察点，用箭头标出观察方向，如下图：

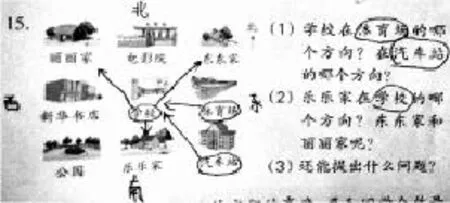
这样学生就很容易弄清“谁在谁的哪个方向？谁的哪个方向是谁？”了。

思过留痕，引导学生在多次写下自己的思维过程和方法中不断积累数学思维经验，实现数学思维的累积性生长，从而从量变逐步走向质变，最终形成良好的数学思维品质，实现数学思维的可持续发展。

在数学教学实践中，我们分别选择了小学二年级、四年级、六年级进行为期一学年的数学学习“思过留痕”实验，实验结果表明，实验班学生数学思维的条理性、全面性、灵活性、系统性和数学表达的清晰性、完整性以及他们在数学课堂上所表现出来的自信心都明显高于同轨平行班级学生，学生作业错误率大大降低，数学成绩明显高于同轨平行班级。

可见，“思过留痕”作为学生数学思维生长的推进器和重要学习策略，可以有效促进学生数学思维的条理性、全面性、灵活性、深刻性、系统化和可持续发展，不断提升学生数学思维品质，避免和减少各种数学作业错误，提高数学成绩。“思过留痕”作为教师了解学生、读懂学生、研究学生进行因材施教的重要教学策略，具有丰富的教育意蕴和实践价值，值得一线数学教师深入探讨和研究。

[1]教育部基础教育课程教材专家工作委员会编写.义务教育数学课程标准（2011年版）解读[M].北京：北京师范大学出版社，2012.

[2]约翰·哈蒂.金莺莲，洪超，裴新宇，译.可见的学习：最大程度地促进学习[M].北京：教育科学出版社，2015.

[3]弗赖登塔尔.陈昌平，唐瑞芬，等，译.作为教育任务的数学[M].上海：上海教育出版社，1995.

[4]刘濯源.基于“思维可视化”的小学生数学核心素养发展策略[J].江苏教育（小学教学），2016（5）：7-9.

[5]刘丽娟.让儿童的思维看得见[J].人民教育，2014（23）：40-42.

（江苏省淮安工业区实验学校 223008）