基于临床数据与循环系统模型融合技术的心血管功能评估中的误差分析

李 逸 殷兆芳 梁夫友#*

1(上海交通大学船舶海洋与建筑工程学院，上海 200240)2(上海交通大学医学院附属上海第九人民医院心内科，上海 200011)

基于临床数据与循环系统模型融合技术的心血管功能评估中的误差分析

李 逸1殷兆芳2梁夫友1#*

1(上海交通大学船舶海洋与建筑工程学院，上海 200240)2(上海交通大学医学院附属上海第九人民医院心内科，上海 200011)

识别影响患者个体化心血管功能评估(基于临床数据与循环系统模型的融合技术)精度的关键因子，并量化分析各因子的影响程度，为评估方法的临床应用提供理论支持。通过参数敏感度分析并结合子集选择方法，识别与血流动力学计算和主要模型参数(与心血管功能的评估目标对应)评估相关的次主要模型参数。利用虚拟临床数据开展数值实验，分析临床数据测量误差(误差区间5%)和次主要参数变动(变动率30%)对主要模型参数评估结果的影响。临床数据的测量误差引起评估结果的显著变化(最大变化率达到16.6%)，相对地，次主要参数变动造成的评估误差较小(在10%以内)。临床数据的精确采集是确保评估结果可靠的关键环节；次主要参数虽然在患者间存在实际的个体差异性，但对其进行固定处理对评估结果的影响较小。

心血管功能评估；循环系统模型；敏感度分析；子集选择；误差分析

引言

在对冠心病和心衰患者的治疗中，心血管功能指标(如心收缩、舒张功能，外周血管阻抗等)是选择治疗时机、进行恰当的术后护理和用药的重要依据[1]。临床上现存多种测量或评估心血管功能的方法，例如：心脏超声可以测量心脏的体积、射血分数等反映心脏形态学特征和心肌收缩力的数据[2-3]； MRI(magnetic resonance imaging)可通过对心肌运动特征的区域化分割处理，识别潜在的缺血区域[4]；另外，BNP(B-type natriuretic peptide，亦称为“客观心功能标志物”)是反映心衰程度的重要生化指标[5]。

人体血液循环系统是由心脏和多种血管构成的闭环系统，各部分的血流参数交互作用，造成在体测量某一项特定心血管功能指标时通常难以摒除其他因素的影响。例如，心脏超声测量的心室射血分数(EF)被认为可以反映心室的收缩力，测量的二尖瓣血流波形频谱可用于判断心室的舒张功能。然而，从系统血流动力学的角度分析，EF和二尖瓣血流波形均受心脏前后负荷(如心室灌注压、外周血管阻抗)的显著影响。特别地，在心室舒张功能异常的进展期会出现二尖瓣血流频谱假性正常化现象，增大了心功能异常的诊断难度。Senzaki等的研究亦表明，分离评估心功能和心脏的负荷条件，对更好地把握患者的心血管功能状态和优化治疗有重要的意义[6]。BNP虽然对诊断心衰有重要的意义，但无法有效识别心收缩或舒张功能不全[7]。迄今为止，关于心脏的固有功能属性在临床上仍没有明确的量化评价指标和对应的测量手段，但在生理学领域已有研究者提出量化分析方法(即elastance理论)[8]，可实现对心脏收缩、舒张功能的量化、分离评估。然而，对elastance的评估通常需要心室容积与压力的时变关系曲线信息[9]，临床可操作性差。

利用循环系统的血流动力学模型，通过逆向工程学的方法分析和整合离散的临床数据，可为上述问题的解决提供可行的途径。前期研究已从数值实验[10]、动物实验[11-13]和体外模型实验[14]等多个方面对该方法进行了探讨，但缺乏对实际临床数据的分析和方法学验证。笔者的研究组在最近的研究中开发了通过融合循环系统模型与临床数据来定量评估患者心血管功能的新算法，并针对少量冠脉搭桥和单心室心脏病患者证明了其可行性[15-16]。在上述研究中，研究者为了克服可利用临床数据资源不足这一问题，采用参数敏感度分析法，从模型参数中识别出与临床测量数据(如大动脉血压、肺动脉血压、心容积等)密切相关的参数(定义为主要参数，其他参数为次要参数)，并将其作为变量来构建参数优化的目标函数。在目标函数的求解过程中，对次要参数进行固定处理是保证函数的解存在且唯一的必要条件。然而，一方面，从生理、病理学的角度考虑，次要参数所代表的心血管功能在不同患者间存在着客观差异性；另一方面，血压、心容积等临床数据包含测量误差，这些因素对求解结果的影响有待进一步研究。

本研究的目的在于考察临床数据测量误差和次要参数变动对心血管功能参数评估结果的影响，研究结果将有助于进一步检验评估算法的可靠性，标定评估结果的误差范围，探明其主导因素，从而为该方法的临床应用奠定理论基础。

1 方法

为了定量地考察评估结果受测量误差和次要参数变动的影响，采用循环系统模型进行随机模拟，生成99组“虚拟患者”数据，导出肺动脉平均压(Pmpp)、左心房平均压(Plap)、大动脉平均压(Pmbp)、左心室收缩末期体积(Vesv)和左心室舒张末期体积(Vedv)等“临床测量数据”，以及对应的主要模型参数值，将其设为数值实验的参照系。另外，鉴于次要参数的数量较大，采用参数敏感度分析法并结合参数间的结构相关度，分析筛选出对模型计算结果和主要参数评估最有影响的数个参数，将其定义为次主要参数。对有限数量的次主要参数进行数值实验，有助于在简化误差分析的同时降低计算负荷。

1.1 循环系统的计算模型

采用研究组在前期研究中使用的循环系统模型[17]。该模型使用一系列集中参数，表达心脏的收缩、舒张功能以及血管的黏性阻抗、顺应性等特性，其电路类比如图1所示。该模型涵盖了循环系统的各主要部分(如心脏四腔、体循环和肺循环)，可保障对心脏与其前后负荷耦合过程的合理描述；同时，模型中的每个参数均与特定的心血管功能对应，有利于定量地分析血压、血流量等血流动力学参数与心血管功能的关系。与更高维度(如一维或三维)的建模方法比较，虽然集中参数建模法无法精确描述局部的血流特征和动脉系统内的血压波传播等现象[18]，但它是唯一可以描述循环系统整体血流动态的方法，而且模型的参数数量可控，利于参数筛选和基于有限的临床数据进行参数校准[19-22]。

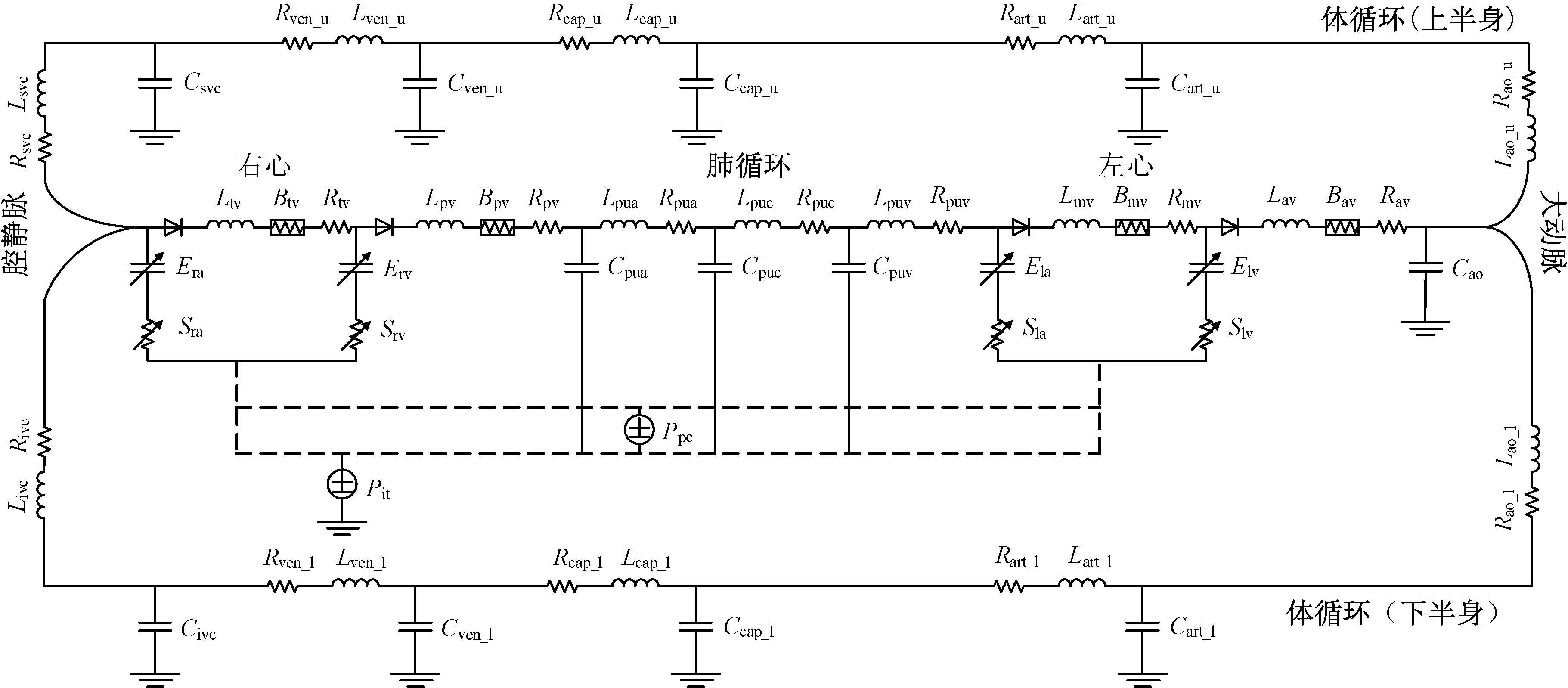
图1 循环系统集中参数模型的电路类比[17]。参数标注：E—倒电容；L—惯性系数；R—黏性阻抗；C—顺应性；B—伯努利阻抗；S—黏弹性系数；Pit—胸内压；Ppc—心包压。下标：ra—右心房；rv—右心室；pua—肺动脉；puc—肺毛细血管；puv—肺静脉；la—左心房；lv—左心室；av—主动脉瓣；mv—二尖瓣；tv—三尖瓣；pv—肺动脉瓣；ao—主动脉；art—动脉；cap—毛细血管；ven—静脉；ivc—下腔静脉；svc—上腔静脉；_l—下半身；_u—上半身Fig.1 Electric circuit analogy of a lumped parameter model of the cardiovascular system[17]. Notation of parameters: E, elastance; L, inertance; R, viscous resistance; C, compliance; B, Bernoulli’s resistance; S, viscoelasticity coefficient; Pit, intra-thoracic pressure; Ppc, pericardial pressure. Subscripts: ra, right atrium; rv, right ventricle; pua, pulmonary artery; puc, pulmonary capillary; puv, pulmonary vein; la, left atrium; lv, left ventricle; av, aortic vavle; mv, mitral valve; tv, tricuspid valve; pv, pulmonary valve; ao, aorta; art, arteries; cap, capillary bed; ven, veins; ivc, inferior vena cava; svc, superior vena cava; _l, lower body; _u, upper body

模型支配方程的构建遵循基本的血流动力学原理[15-17]。心脏的4个房室的收缩和舒张功能采用时变的倒电容(即elastance)来表达，通过心脏内的血液容积计算心脏内压，并进一步通过心脏瓣膜模型与外周血管的血流动力学参数关联。血管内血流的支配方程基于流经每个血管区段血流的质量和动量守恒原理构建，所有方程构成一个非线性的常微分方程组，采用四阶龙格-库塔法求解。关于模型支配方程和数值算法的更详细信息，可参考研究组的前期工作[15-17]。

1.2 临床数据及患者个体化评估

1.2.1 临床数据

本研究主要利用心脏病诊疗流程中采集的临床数据，包括大动脉压(由动脉导管采集)、肺动脉压、肺毛细血管楔压(由静脉导管采集)和左心室体积(由心脏超声测量)。为了使模型可以精确地拟合临床数据，有必要分析临床数据与模型计算结果的对应关系。例如，考虑集中参数模型描述血管内脉搏波传播的局限性，取大动脉压、肺动脉压在一个心动周期内的平均值而非血压波形作为拟合目标；另外，由于本模型未包含肺毛细血管楔压的计算模块，假定肺毛细血管楔压与左心房平均压一致(可由模型计算获得)。最终用于模型参数评估的临床数据包括：肺动脉平均压(Pmpp)、左心房平均压(Plap)、大动脉平均压(Pmbp)、左心室收缩末期体积(Vesv)和左心室舒张末期体积(Vedv)。

1.2.2 主要参数识别与参数优化

采用的循环系统模型由58个参数构成，而可利用的临床数据仅有5项，即基于临床数据构建的5个参数优化目标函数包含58个变量。根据代数方程理论，该方程组不封闭，没有唯一解存在。本研究所开展的数值实验也证明，目标函数的解随模型初始条件的改变而变化，无法唯一地确定模型参数。为了解决该问题，对模型系统进行了参数敏感度分析，从中选取与临床数据的模型计算结果最相关的数个模型参数，设定为主要参数，即体循环血管顺应性(Csys)、左心室基准elastance(Elvb)、左心室收缩期elastance振幅(Elva)、体循环阻抗(Rsys)、肺循环阻抗(Rpul)，其他参数设为次要参数。根据临床数据和主要参数，构建的参数优化目标函数为

(1)

式中，Xe(xe,1,xe,2…xe,5)和X0(x0,1,x0,2…x0,53)分别表示主要参数向量和次要参数向量，在此，Xe为目标函数的变量，X0为常数(默认值)，Pj和Yj分别表示模型计算结果和临床实测值，对应着肺动脉平均压和左心室体积等。

由于目标函数是包含多个变量的非线性方程组，本研究采用改良的Nelder-Mead法进行求解[16]，求解所得Xe值即为与临床数据(Yj)对应的患者个体化心血管功能参数。

1.3 虚拟临床数据的生成

如前所述，笔者的主要目的是研究临床数据测量误差和次要参数变动对主要参数估测值的影响，为此目的，需要有主要参数值作为已知条件和参照系，以便开展定量分析。然而，在实测的临床数据中缺乏心血管功能参数信息，无法开展上述研究。为了解决这一问题，采用循环系统模型生成一系列虚拟的临床数据，并记录其所对应的心血管功能参数，构建分析估测误差的参照系。具体来说，在模型计算中，对主要模型参数在其生理范围内进行随机变动(相对其默认值在20%～200%间变动)，并求解肺动脉平均压、左心房压和左心室体积等，将其作为虚拟的临床数据。利用该方法，共生成了符合统计学要求的99组虚拟临床数据，每组数据均包含病人标号(n)、性别(sex)、体重(wight)、身高(hight)、心动周期(Tduration)、肺动脉平均压(Pmpp)、左心房平均压(Plap)、大动脉平均压(Pmbp)、左心室收缩末期体积(Vesv)、左心室舒张末期体积(Vedv)等信息。各项虚拟数据的分布区间和统计结果(表示为mean±SD)如下：肺动脉平均压[12.1,37.2](22.7±6.7)[mmHg]，左心房压[7.9,30.9](15.3±5.5)[mmHg]，大动脉平均压[33.2,190.8](98.3±38.7)[mmHg]，左心室收缩末期体积[12.6,217.7](57.9±36.1)[ml]，左心室舒张末期体积 [109.3,463.2](217.7±74.7)[ml]。上述数据覆盖了临床所见血压和心室容积的主要变动范围，并且不同组间的数值变异显著，因此可以较好地体现实际患者间的个体差异性。

1.4 次主要参数的筛选

本研究采用参数敏感度分析和子集选择相结合的方法，识别对临床数据的模型仿真结果影响较大同时与主要参数相关的次主要参数。

1.4.1 参数敏感度分析

由于循环系统是复杂的非线性系统，模型参数的敏感性与系统状态有关，因此在单一心血管功能状态下开展的参数敏感度分析有漏选某些重要参数的风险[16]。为了解决上述问题，首先采用Latin-Hypercube全域参数取样技术[23]，对关键模型参数(5个主要参数+20个次要参数(根据其生理意义选择))在其生理范围内进行随机变动，生成100组模型参数子集来表达多种心血管功能状态，从而构成进行全域参数敏感度分析的参数空间。需要指出，虽然进一步增加参数组合可以提高数据的分割精度(研究组在前期工作中采用了3000组数据[16])，但会增大敏感度矩阵的复杂性及后续的数据分析难度。Latin-Hypercube取样技术的优势在于可以利用有限数量的数据构成反映参数全域变动属性的数据空间，本研究开展的数值实验亦表明，在参数分布区间不变的条件下，将参数组合由100组增大至1 000组识别出的敏感参数不变。在上述参数空间内，通过模型仿真考察每个参数变动(本研究采用的变化率为Δ=5%)而引起的肺动脉平均压(Pmpp)、左心房平均压(Plap)等的变化率。最后，通过统计学分析计算Pmpp、Plap等对每个参数的敏感度指数。

对每项临床数据，其参数敏感度指数定义为

(2)

式中，y表示与临床数据对应的模型计算值，θ表示模型参数，下标i(=1,M),j(=1,N)分别表示模型参数子集的序列号和各参数在模型中的标号，得到敏感度矩阵表示为

(3)

式中，M=100，N=58。

表1 次主要参数筛选列表Table 1 List of secondary major parameters

1.4.2 子集选择

虽然准次主要参数对临床数据的模型计算结果影响较大，但对主要参数估测结果的影响程度未知。为了明确其对主要参数估测结果的影响，同时进一步减少拟分析次要参数的数量，本研究引入了子集选择方法。子集选择有结构相关度分析、特征值分解以及特征向量子空间分析等方法[24]。考虑本研究的目的，采用了结构相关度分析法计算所有模型参数与主要参数的相关度γ，γ值越大，则两参数间的相关度越大。

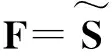
(4)

1.5 对主要参数评估结果的影响

1.5.1 临床测量误差

将虚拟临床数据的每项数据(即肺动脉平均压(Pmpp)、左心房平均压(Plap)、大动脉平均压(Pmbp)、左心室收缩末期体积(Vesv)和左心室舒张末期体积(Vedv))分别施加5%的测量误差(临床测量误差一般处于0～5%之间[12])，利用参数优化算法重新评估主要参数(即体循环血管顺应性(Csys)、左心室基准elastance(Elvb，反映左心室的舒张功能)、左心室收缩期elastance振幅(Elva，反映左心室的收缩功能)、体循环阻抗(Rsys)、肺循环阻抗(Rpul)，并与主要参数的参照值比较，计算评估结果的变化率(以百分比计)。最后，对基于99组虚拟临床数据的求解结果进行统计学分析，计算变化率的平均值及标准差(mean±SD)。

1.5.2 次主要参数变动

对表1中的7个次主要参数(即右心室基准elastance(Ervb)、右心房基准elastance(Erab)、右心室收缩期elastance振幅(Erva)、左心房收缩期elastance振幅(Elaa)、下腔静脉阻抗(Rvca_l)、左心房基准elastance(Elab)、右心房收缩期elastance振幅(Eraa))，在其默认值的基础上分别施加30%的变化，同时保持虚拟临床数据的值不变，重新评估主要参数并计算评估结果的变化率。最后，对基于99组虚拟临床数据的求解结果进行统计学分析，计算其平均值及标准差(mean±SD)。

2 结果

2.1 临床测量误差的影响

图2表示各项临床数据存在5%的测量误差时主要参数评估结果的变化率。由图可知，测量误差可引起主要参数评估结果的显著变化。其中，肺动脉平均压(Pmpp)的测量误差对肺循环阻抗估测值的影响最大，达到16.6%；左心房平均压(Plap)的测量误差对肺循环阻抗和左心室基准elastance评估结果的影响较大，分别为11.4%和8.8%；大动脉平均压(Pmbp)的测量误差对体循环阻抗的评估结果影响显著，为9.7%；左心室舒张末期体积(Vedv)的测量误差对各参数评估结果的影响均较明显，变化率在3.5%～10.3%之间。相对来说，左心室收缩末期体积(Vesv)的测量误差影响较小，仅显著影响左心室收缩期elastance振幅(Elva)的评估结果。

值得注意的是，测量误差引起的评估结果变化率与所使用的临床数据有关，在特定情况下(如Pmpp和Plap的测量误差对肺循环阻抗的影响)，若标准差大于平均值，则提示测量误差对参数评估结果的影响程度与心血管功能状态有关，即存在个体差异性。

2.2 次主要参数变动的影响

图3显示了将次主要参数的值变动30%后主要参数的估测结果相对其参照值的变化率。整体而言，次主要参数变动所引起的评估结果变化率较小，最大值为7.4%。体循环血管顺应性(Csys)的评估结果受右心室功能(Ervb，Erva)的影响相对明显，而左心房基准elastance(Elab)的变动对左心室基准elastance(Elvb)的评估结果也有较为显著的影响。

图2 临床测量数据存在5%误差时主要参数估测值的变化率Fig.2 Changes in estimated main parameters as 5% errors are introduced to the clinical data

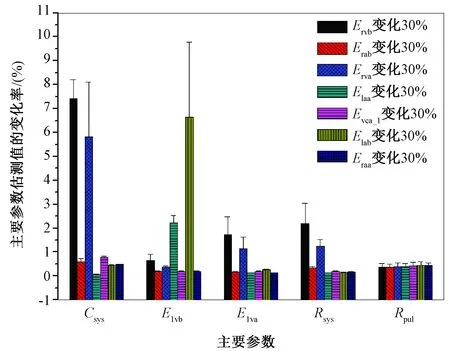
图3 次主要参数变化30%时主要参数估测值的变化率Fig.3 Changes in estimated main parameters as secondary main parameters are varied by 30%

3 讨论

基于临床数据对循环系统的计算模型进行患者个体化校准或评估患者的心血管功能，已成为心血管生物力学领域的一个研究热点[27-28]。由于可利用的临床数据有限，研究人员通常需要对模型进行简化处理，或构建仅包含有限数量模型参数的目标函数，以使参数优化算法收敛于唯一的解[24,29]。在最近的研究中，笔者的研究组发展了通过融合临床数据和循环系统理论模型来评估患者心血管功能的方法[15-16]。在上述研究中，参数优化仅针对特定的模型参数(即主要参数)，忽略了临床数据的测量误差和其他参数(即次要参数)对评估结果的影响。实际上，任何临床数据的测量均无法避免不确定误差的存在，而次要参数所表达的心血管功能在患者间存在差异，这些因素对主要参数评估结果的影响有待量化分析，以明确该评估方法的临床应用价值或发现其潜在问题。为了研究上述问题，笔者进一步发展了针对测量误差和参数变动的误差分析方法，其间开发了通过参数敏感度分析与子集选择相结合来挑选次主要参数的方法，从而有效降低了计算负担，简化了误差分析过程。

本研究的数值实验表明，测量误差对主要参数的评估结果有显著的影响，并且研究结果与循环系统血流动力学知识吻合，部分验证了所开发的误差分析方法的有效性。例如，肺动脉压和左心房压共同决定肺循环的压力梯度，因此对肺循环阻抗的评估结果影响显著，左心房压和左心室舒张末期体积是反映左心室舒张功能的间接指标，本研究的结果亦表明两者的测量误差对左心室基准elastance(反映左心室的僵硬度，指示舒张功能)的评估结果影响最大。基于上述发现，笔者认为，在实际应用中，对可能存在较大测量误差的临床数据，需要在恰当评估测量误差影响的基础上，解释参数优化结果。与临床数据的测量误差比较，次主要参数变动对评估结果的影响相对较小，即使变动了30%，所引起的最大评估误差也在10%以内。该发现表明，虽然次要参数可能在不同患者间差异明显，但在主要参数的评估计算中固定这些参数对评估结果的影响不大，证明课题组开发的以主要参数为目标的参数评估方法有较好的鲁棒性。

本研究的局限性主要体现在两个方面。首先，基于有限的虚拟临床数据开展误差分析研究，无法涵盖所有患者的心血管功能状态；其次，在进行误差分析时，每组数值实验仅针对某一项临床数据的测量误差或某个模型参数的变动，未研究多项临床数据同时存在误差或多个模型参数同时变动时评估结果的变化规律。由于人体血液循环系统呈现高度非线性特征，各心血管功能参数间相互影响，无法通过线性叠加的方法来拓展现有的研究结果。为了弥补上述不足，需要在后续的研究中，在进一步扩大样本数据的基础上，引入多项测量误差和多参数变动，以提高研究结果的统计学意义。

4 结论

为了弥补前期患者个体化心血管功能评估研究在参数依存性和误差分析方面的不足，本研究进一步发展了次主要参数的识别方法，并量化分析了由临床数据的测量误差和模型参数变动引起的评估误差。研究结果表明，临床数据的测量误差显著影响评估结果，相对地，评估结果受次主要参数变动(或患者个体差异性)的影响程度较低。因此，确保临床数据的采集精度，将是决定患者个体化心血管功能评估的临床应用效果的关键环节，而本研究的发现也为解释评估结果和分析误差提供了理论依据。在后续的研究中，将进一步考察多项测量误差共存和多参数变动对评估结果的综合影响。

(致谢 上海交通大学刘浩教授、上海第九人民医院心内科范虞琪医师为本研究的开展和论文撰写提供了宝贵的意见和建议，在此表示衷心的感谢。)

[1] Evonich RF, Stephens JC, Merhi W, et al. The role of temporary biventricular pacing in the cardiac surgical patient with severely reduced left ventricular systolic function[J]. Journal of Thoracic and Cardiovascular Surgery, 2008, 136(4):915-921.

[2] Pavlicek M, Wahl A, Rutz T, et al. Right ventricular systolic function assessment: rank of echocardiographic methods vs cardiac magnetic resonance imaging [J]. European Journal of Echocardiography, 2011, 12(11):871-880.

[3] Vitarelli A, Conde Y, Cimino E, et al. Quantitative assessment of systolic and diastolic ventricular function with tissue Doppler imaging after Fontan type of operation [J]. International Journal of Cardiology, 2005, 102(1):61-69.

[4] Natsume T, Amano T, Takehara Y, et al. Quantitative assessment of regional systolic and diastolic functions and temporal heterogeneity of myocardial contraction in patients with myocardial infarction using cine magnetic resonance imaging and Fourier fitting [J]. Magnetic Resonance Imaging, 2009, 27(10):1440-1446.

[5] Vodovar N, Séronde MF, Laribi S, et al. Elevated plasma B-type natriuretic peptide concentrations directly inhibit circulating neprilysin activity in heart failure [J]. JACC: Heart Failure, 2015, 3(8):629-636.

[6] Senzaki H, Chen C, Masutani S, et al. Assessment of cardiovascular dynamics by pressure-area relations in pediatric patients with congenital heart disease [J]. Journal of Thoracic and Cardiovascular Surgery, 2001, 122(3):535-547.

[7] Troughton RW, Prior DL, Pereira JJ, et al. Plasma B-type natriuretic peptide levels in systolic heart failure: importance of left ventricular diastolic function and right ventricular systolic function [J]. J Am Coll Cardiol, 2004, 43(3):416-422.

[8] Suga H, Sagawa K, Shoukas AA. Load independence of the instantaneous pressure-volume ratio of the canine left ventricle and effects of epinephrine and heart rate on the ratio [J]. Circulation Research, 1973,32:314-322.

[9] Senzaki H, Chen CH, Kass DA. Single-beat estimation of end-systolic pressure-volume relation in humans: A new method with the potential for noninvasive application [J]. Circulation, 1996, 94(10):2497-2506.

[10] Xiao X, Ozawa ET, Huang Y, et al. Model-based assessment of cardiovascular health from noninvasive measurements [J]. Ann Biomed Eng, 2002, 30(5):612-623.

[11] Hann CE, Revie J, Stevenson D, et al. Patient specific identification of the cardiac driver function in a cardiovascular system model[J]. Computer Methods and Programs in Biomedicine, 2011, 101(2):201-207.

[12] Revie J, Stevenson D, Chase JG, et al. Validation of subject-specific cardiovascular system models from porcine measurements[J]. Computer Methods and Programs in Biomedicine, 2013, 109(2):197-210.

[13] Chase JG, Lambermont B, Starfinger C, et al. Subject-specific cardiovascular system model-based identification and diagnosis of septic shock with a minimally invasive data set: animal experiments and proof of concept[J]. Physiological Measurement, 2011, 32(1):65-82.

[14] Yu YC, Boston JR, Simaan MA, et al. Minimally invasive estimation of systemic vascular parameters[J]. Ann Biomed Eng, 2001, 29(7):595-606.

[15] Sughimoto K, Liang F, Takahara Y, et al. Assessment of cardiovascular function by combining clinical data with a computational model of the cardiovascular system[J]. Journal of Thoracic and Cardiovascular Surgery, 2013, 145(5):1367-1372.

[16] Liang F, Sughimoto K, Matsuo K, et al. Patient-specific assessment of cardiovascular function by combination of clinical data and computational model with applications to patients undergoing Fontan operation[J]. International Journal for Numerical Methods in Biomedical Engineering, 2014, 30(10):1000-1018.

[17] Liang F, Senzaki H, Kurishima C, et al. Hemodynamic performance of the Fontan circulation compared with a normal biventricular circulation: a computational model study[J]. American Journal of Physiology-Heart and Circulatory Physiology, 2014，307(7), H1056-H1072.

[18] Liang F, Oshima M, Huang H, et al. Numerical study of cerebroarterial hemodynamic changes following carotid artery operation: A comparison between multiscale modeling and stand-alone three-dimensional modeling [J]. Journal of Biomechanical Engineering, 2015, 137(10):101011.

[19] 樊瑜波，陈君楷，袁支润，等. 全分支的体循环混合参数计算机模拟研究[J]. 生物医学工程学杂志，1995,12(3)：128-223.

[20] 丁光宏，魏岗之. 脑循环脉动流的集中参数模型[J]. 力学学报，1996,28(3)：336-346.

[21] 王盛章，姚伟，丁光宏. 脑血流自动调节功能的三单元模型[J]. 医用生物力学，2007,22(3)：268-272.

[22] 谷凯云，高斌，刘有军，等. 基于主动脉内血泵的集中参数模型研究[J]. 医用生物力学, 2011, 26(4):367-372.

[23] Van Griensven A, Meixner T, Grunwald S, et al. A global sensitivity analysis tool for the parameters of multi-variable catchment models [J]. Journal of Hydrology, 2006, 324(1):10-23.

[24] Olufsen MS, Ottesen JT. A practical approach to parameter estimation applied to model predicting heart rate regulation[J]. Journal of Mathematical Biology, 2013, 67(1):39-68.

[25] Cintron-Arias A, Banks HT, Capaldi A, et al. A sensitivity matrix based methodology for inverse problem formulation[J]. Journal of Inverse and Ill-posed Problems, 2009, 17(6):545-564.

[26] Yue H, Brown M, Knowles J, et al. Insights into the behavior of systems biology models from dynamic sensitivity and identifiability analysis: a case study of an NF-kB signaling pathway[J]. Mol Biosyst, 2006, 2(12):640-649.

[27] Pennati G, Corsini C, Cosentino D, et al. Boundary conditions of patient-specific fluid dynamics modeling of cavopulmonary connections: possible adaptation of pulmonary resistances results in a critical issue for a virtual surgical planning [J]. Interface Focus, 2011, 1(3):297-307.

[28] Sun Qi, Liu Jinlong, Qian Yi, et al. Computational haemodynamic analysis of patient-specific virtual operations for total cavopulmonary connection with dual superior venae cavae [J]. European Journal of Cardio-Thoracic Surgery, 2014, 45(3):564-569.

[29] Pope SR, Ellwein LM, Zapata CL, et al. Estimation and identification of parameters in a lumped cerebrovascular model[J]. Math Biosci Eng, 2009, 6(1):93-115.

Error Analysis on the Assessment of Cardiovascular Function Based on Integration of Clinical Data and Cardiovascular Model

Li Yi1Yin Zhaofang2Liang Fuyou1#*

1(SchoolofNavalArchitecture,OceanandCivilEngineering,ShanghaiJiaoTongUniversity,Shanghai200240,China)2(DepartmentofCardiology,ShanghaiNinthPeople’sHospital,ShanghaiJiaoTongUniversity,Shanghai200011,China)

The purpose of this study is to identify the key factors that affect the accuracy of patient-specific assessment of cardiovascular function (by means of integration of clinical data and cardiovascular model) and quantify their effects so as to provide theoretical evidence for guiding the clinical application of the assessment method. Parameter sensitivity analysis was performed in combination with parameter subset selection to identify the secondary main parameters that are related closely to the model-based prediction of hemodynamic variables and the assessment of the main parameters (corresponding to the assessed cardiovascular function). Numerical experiments were carried out based on a series of virtual clinical data to quantify the changes in assessment results induced by measurement errors (in a range of 5%) of clinical data and variations in the secondary main parameters (rate of change being 30%). Measurement errors of clinical data were found to induce pronounced changes in assessment results (up to 16.6%), relatively, variations in the secondary main parameters had less influence on the assessment (rates of changes being within 10%). Accurate clinical data measurement is a key step to guaranteeing the reliability of cardiovascular function assessment. The secondary main parameters only have limited influence on the assessment although they may vary significantly among patients.

Assessment of cardiovascular function; cardiovascular model; sensitivity analysis; subset selection; error analysis

10.3969/j.issn.0258-8021. 2016. 01.006

2015-09-13， 录用日期:2015-11-29

国家自然科学基金项目(81370438)；上海交通大学医工交叉研究基金项目(YG2012MS24)

R318

A

0258-8021(2016) 01-0047-08

# 中国生物医学工程学会会员(Member, Chinese Society of Biomedical Engineering)

*通信作者(Corresponding author)， E-mail: fuyouliang@sjtu.edu.cn