探寻学生“思考路径”背后的思考

□孙佳威 付春红

探寻学生“思考路径”背后的思考

□孙佳威 付春红

在实际教学中，教师经常会遭遇“理想与现实”的尴尬窘况：学生在学习一个新的知识后，往往学起来感觉很容易，但真正在解决问题时又显得很困难，形成了极大的效果反差。因此，教师在教学中要真正顺应学生的思维，关注学生的学习路径。通过以学生用“平均数”解决问题的路径为研究点，充分展示学生的思考路径，以此为“砖”，引发思考，提出课堂教学要关注学生思考问题的方式和路径，发出了“顺应学生思维”架构课堂的声音。

平均数 解决问题 思考路径

“平均数”是人教版小学数学四年级的教学内容，是统计与概率领域中的一个重要的概念。在实际教学中我们发现，学生在理解“平均数”的概念、计算平均数时总是能够做到轻而易举、百发百中，可是在应用这个概念解决问题时却又不尽如人意。尽管我们为学生提供了、讲解了、巩固了一个又一个的优质方法，可一部分学生在面对实际问题时依然不知所措，离我们的理想相去甚远。这么大的效果反差，引起了我们的思考：是教学方法出了问题？是我们不了解学生？是我们的方法不够优质？……学生在解决与这个概念相关的问题时思考的路径是怎样的呢？带着这些问题，我们利用一道题目对学生的学习路径进行了深度的探寻。

测试题目：

此题的设计没有评价学生是否会计算平均数，而是把评价的目标放在了对平均数意义的理解上，通过对平均数意义的理解来解决问题。此题正确率为75.09%。学生是怎样思考的呢？为了更好地展示“冷静”数据背后的“火热”，我们对120名学生进行了追踪，现将学生的思考过程展示出来，并进行学生学习路径分析。路径一：假设法，确定平均数。

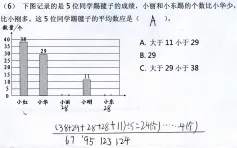
图1

图2

图3

在参与调研的120名学生中，有10名学生采用了假设的方法来解决问题。

从图上我们可以看出，面对这个问题时，学生的入手点,都是根据要求将小丽和小东设成符合条件（在11～29之间）的数，再求平均数。虽然学生在设数的过程中有所不同：有的学生设一个大数、一个小数；有的学生设成两个比较大的数；有的学生则设的是两个数之间的平均数，但是用的都是假设法，都是在通过对求平均数的方法的重现解决问题。那学生是怎么想到要用到假设法的呢？为了了解学生的真实想法，我们对其中的1名学生进行了调研。

师：你是怎么解答这道题目的？

生：我是先把每个数都写出来，然后加起来，再除以几个人的数就行了。

师：你是怎样想到要这样做的？

生：因为求平均数就是要先把这几个人的数加起来，然后再除以这几个人。

师：你对计算平均数方法很熟悉，可是我们题目中没有把每个数都说出来，你怎么能算出平均数呢？

生：虽然没给数，可是题目中说了“小丽和小东踢的个数比小华少，比小刚多”，所以我就按照要求先把小丽和小东的数都假设成一个数，这个数比29少比11多就行了，这样就能列算式计算了。

通过对话可以看出，学生对计算平均数的方法的掌握还是很牢固的，他们试图通过已知的计算方法找到解题思路。在这个学生的心目中，要计算平均数就要先有数据，题目中没有直接给出数据，那么就要根据给出的信息找到一个符合条件的数据，通过计算出确切的数值进行选项的判断。

路径二：移多补少，确定平均数。

在被追踪的120名学生中有30人采用了这个方法，比较典型的方法如下：

从图上我们可以直观地感受到学生在尝试运用“移多补少”的方法解决问题，他们是怎样想到的呢？带着这个疑问我们对图4这个学生进行了追踪访谈。

师：让你找到他们的平均数，你这是干嘛呢？（手指里面的加法和减法算式）

生：我想把多的给少的，这样就能找到平均数。

师：你是怎样想到要这样做的呢？

图4

图5

生：在上课时，老师给我们讲平均数时就是这样找的。

师：怎样找的？

生：就是移多补少找的，那时候是说水深的事情，把高处的土移到低处去，然后河的底下就平了，老师告诉我们这个平的河底的水深就是平均数。

师：看来移多补少在你心中留下了深刻印象，可是这道题中小丽和小东的条形都是空的，你怎么还能够通过移多补少找到他们平均数的范围呢？

生：这里38是最大的，所以肯定得给最少的小刚补上，给他9个，就是29个了，而小刚得到后才18个，小丽和小东在29和11之间，再怎么移多补少，他们几个人的平均数也是比29少，比11多，所以能够确定他们的平均数在11～29之间。

师：你说小红给小刚9个，小刚才18个，为什么要加上一个‘才’字，你想说明什么？

生：就是给完了也是少，其他的再怎么匀乎匀乎还是在这个范围内。

我们都清楚地知道，对于平均数可以简单地理解为：平就是拉平，均就是相等。即几个不相等的数在“和”不变的情况下，通过移多补少而变得相等，这个相等的数就是平均数。这样一个抽象的问题，学生通过对课堂学习情景的再现，把移多补少的过程巧妙地迁移到了这道题中。正是对“学习过程”的生动再现与巧妙迁移，才使得他们在解决这样一道看似“无法”的问题时多了一条路径。

路径三：意义加特点，确定平均数

平均数介于最大数和最小数之间，能较好地反映一组数据的总体情况，是一个虚拟的数。依据平均数的这一意义、特点，学生能否寻找到解决问题的路径呢？

通过追踪我们发现，120名学生中有80人采用了这个方法，通过对比，我们找到了2个最具有代表性的学生的作品。

图6

图7

针对其中的2名学生我们进行了访谈。

访谈一：针对图6学生的访谈。

师：题目让你们找到这组数据的平均数，你也没有计算的过程，也没有找全这组数据，怎么就准确地说出这组数据的平均数是在11～29之间。

生：因为平均数就是一个平均情况，是这组数据的一个情况（学生对于整体情况这件事虽然不会准确描述，但是能够感受到平均数的本质内涵）。从题中可以看出小丽和小东都在29以下，11以上，所以这组数据中虽然有1个人是38个比较大，但是其他4人都比38少很多，这样一看，不用算也知道整体上不会超过29，也不会比11少，所以我认为应该选择A。

由这个学生的回答，我们可以清楚地感受到“平均数反映的是这组数据的总体情况”这件事已经在他的心目中生根发芽，应用起来也是得心应手。

图7学生解决问题的方式似乎和图6学生相同，但是他的表达方式似乎更加抽象一些，他又是怎样想的呢？下面是我们的访谈实录。

访谈二：针对图7学生的访谈。

师：这道题让你找到这组数据的平均数，你怎么就写了一个大部分就知道了，这个大部分是什么意思？

生：因为平均数是一组数据的情况，是这些数据匀乎完了的数值，在这几个人中，就一个38比较大，其他的数好几个都是11～29之间的数，就是小红一人多点，她一人给他们匀乎也匀不了多少，也不能改变什么。所以说，他们的总体情况还是不会变什么，得听大多数的，所以选择A。

师：你说的听大多数的是不是就是你题中写的——

生：大部分。

师：是永远都听大部分的吗？这个少数人就不起任何作用吗？

生：小红虽然多，但是只是一点，对于这个整体不起太大作用，改变不了什么。

师：你觉得什么时候会改变点什么？

生：除非她特别多或者特别少，才能把那些“大部分”变大或者变小。

通过对图6和图7两位同学的访谈我们可以看出，对于平均数的本质内涵：在最大数和最小数之间，较好地反映一组数据的总体情况，学生已经非常熟悉，并且能够运用这个特性正确分析数据特点，灵活解决问题。

通过对上面这3种路径的分析，我们发现学生在解决这个问题时，或是根据平均数的计算方法进行数据的假设，或是根据平均数得来的过程进行数据的“拼补”，或是根据对平均数意义的理解进行推测，不同特质的学生采用了不同的解决问题的路径。但是这些方法没有一个是教师手把手教的，而是学生在对基本概念理解的基础上的一种“独创”的“好”方法，学生的学习有自己的思维路径。

回想我们的课堂教学，我们很少真正思考学生需要的是什么？他们自己有哪些更好的方法和策略？我们总想着塞给学生一个更好的策略或者思路，总想着帮助学生尽早地择优一下，总想着拽着学生跳过沟壑，少走弯路。费尽心机、呕心沥血后，一旦放手，学生仍然不能很好地解决问题，我们不由得仰天长叹：怎么就教不会呢？其实是我们不会教。从今天的学生研究中我们看出，不同特质的学生自己会去寻找不同路径，寻找一条适合自己的“出路”。而我们的手把手的背后，是对学生思维的禁锢。

有了这样的学生研究，我们才真正读懂了探求学生内心世界的重要。回归学生的内心世界，重构我们的课堂教学，我们发现：与其费尽心机让学生理解我们的想法，不如顺其自然和学生一起走在数学的路上，顺应学生的思维，尝试接纳他们的想法，站在他们的角度巧妙引导，我们也许会收获得更多。

（北京市朝阳区教育研究中心100020北京市朝阳区望京南湖东园小学100020）