基于粒子滤波的涡扇发动机健康诊断

杨 蓓，张宸宇

(南昌航空大学 飞行器工程学院，南昌 330063)

基于粒子滤波的涡扇发动机健康诊断

杨 蓓，张宸宇

(南昌航空大学 飞行器工程学院，南昌 330063)

采用粒子滤波算法，设计了一种无需涡扇发动机线性化模型的故障诊断方法。通过含有高斯白噪声的转速测量信号准确估计出相应转速值，构造残差，并设定合适的阈值，实现了故障诊断。压气机健康诊断仿真结果表明：高压压气机(HPC)效率突变30%会导致残差信号1 000倍以上的变化，可以明显检测到故障的发生及发生时刻；当HPC效率突变量为2%，残差信号将变成正常时的6倍，残差信号还可以反映退化程度。因此基于非线性粒子滤波的发动机健康诊断方法可较好地辨识发动机性能退化、故障及失效。

粒子滤波；残差；涡扇发动机；故障诊断；非线性模型

0 引言

随着涡扇发动机设计水平和制造工艺的不断提高，其结构也变得更加复杂，在恶劣的飞行条件和高温高压的工作环境下，不可避免地会发生各种故障，甚至引发飞行事故(其寿命和推力、耗油率等性能不断衰退)。有关飞行器调查结果表明，气路系统故障在涡扇发动机总故障中占有极高的比例，发动机故障约占飞机故障的36%[1-3]。积极开展发动机健康管理工作已成航空领域发展趋势[4]。发动机故障诊断主要通过测量参数的变化估计性能参数的变化，进而分析判断发动机各个部件的状况。

在各种故障诊断方法中，基于模型的故障诊断方法始终是国内外的研究热点[5]。采用基于线性近似方法的传统故障诊断策略得到了较为成熟的研究，卡尔曼滤波算法是其中之一。在面对非线性较强的涡扇发动机以及非高斯的过程与测量噪声时，可以采用扩展卡尔曼滤波。现代系统越来越复杂，涡扇发动机热力学过程也表现出强非线性特点。扩展卡尔曼滤波可以应用于简单非线性系统，但无法确保其收敛性[5]。无迹卡尔曼滤波应用于非线性系统通过概率密度函数进行，无需线性化，但同样不适用于非高斯分布的系统[1]。

基于非线性滤波的故障诊断方法是近年来一个重要研究方向，也取得了较多的研究成果。粒子滤波的核心思想在于用随机样本来描述概率分布[3]，不断调整各个样本和对应权值的取值，并将样本均值作为系统估计值。基于Monte-Carlo方法的粒子滤波算法已成为非线性、非高斯动态系统状态估计的一种有效方法。粒子滤波能有效克服传统故障诊断方法对于非线性、非高斯分布系统的诊断缺陷。粒子滤波计算量大导致的难以应用的问题随着计算机性能的不断提高得到解决，并逐渐被广泛应用于目标跟踪、故障诊断与隔离、系统辨识等领域[5-7]。

1 粒子滤波基本原理

粒子滤波方法是通过优化获得一组分布于状态空间的随机样本，以对概率密度函数进行近似。采用样本均值代替积分运算，获得最小方差。粒子滤波的核心步骤是基于Monte-Carlo方法，假设系统的状态空间模型为[1,8]：

(1)

式中：ωk,vk分别表示系统的过程干扰和测量噪声；xk,xk+1分别表示系统在k和(k+1)时刻的状态变量；uk为系统在k时刻的输入值；zk为系统在k时刻的测量值。

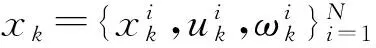
(2)

权值根据重采样等方法确定：

(3)

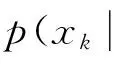
标准粒子滤波算法步骤为[7,9-10]：

1)状态预测。从系统状态转移概率密度中抽取所需粒子，即

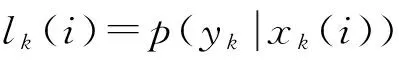
3)更新各个粒子权值并归一化。

4)粒子重采样。

2 粒子滤波在发动机故障诊断方面的应用

当式(2)的概率密度随着测量值逐步改变，则可通过粒子均值代替上一步的后验概率密度函数积分值，以得到最小方差估计。发动机故障诊断所构造的残差信号是通过粒子滤波算法获得的估计值与实际测量值进行对比获得。当部件发生故障时，所测量信号会出现突变(快速变大或变小)，在滤波工作过程中，估计值需要重新迭代才能收敛于新的测量值，据此构造残差信号(zk-xk+1)[11]。整个故障诊断系统需要建立相应的带故障部件的发动机数学模型。当系统变量可测时，构造如下滤波器：

(4)

(5)

由式(4)、式(5)可得系统的残差输出信号：

(6)

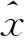
(7)

经过粒子滤波后，粒子滤波估计值收敛于测量值，此时可为残差设定合适的阈值。当残差大于该阈值时，判定系统发生故障，反之则判定无故障[10]。

3 仿真结果与分析

3.1 粒子滤波参数跟踪效果分析

以涡扇发动机模型为对象进行粒子滤波估计与故障诊断，发动机动态过程模型中需要考虑转子的惯性，从而获得转子动力学方程式(8)：

(8)

式中：JH、JL分别为发动机高压转子和低压转子的转动惯量；ΔMH，ΔML分比为高低压转子的剩余力矩。以转子动力学方程(8)为基础，结合质量流量连续方程，并采用GSP中的共同工作线以及特性数据，最终可以得到形如式(9)的发动机非线性表示模型[12-13]：

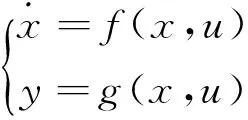
(9)

根据发动机特性，高低压转子的剩余力矩为：

(10)

涡扇发动机的压气机、涡轮等部件的退化或者故障都会在转速上有所反映，因此此处选择转速作为输出，则式(9)可改写为：

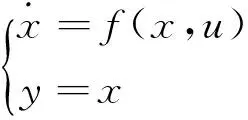
(11)

在仿真粒子滤波参数估计效果时，设定发动机燃油流量从32%增加到102%，观察其转速估计效果。选定粒子数为100，采样点选择30个。在初始时刻，随机分布的粒子(使转速分布范围为0～16 000 r/min)如图1所示。

在完成30步运行之后，粒子滤波估计的转速与实际测得的转速如图2所示。图2中延伸到最

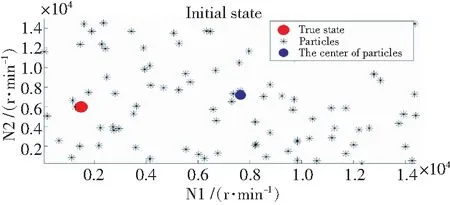
图1 初始粒子分布Fig.1 Initial distribution of particles

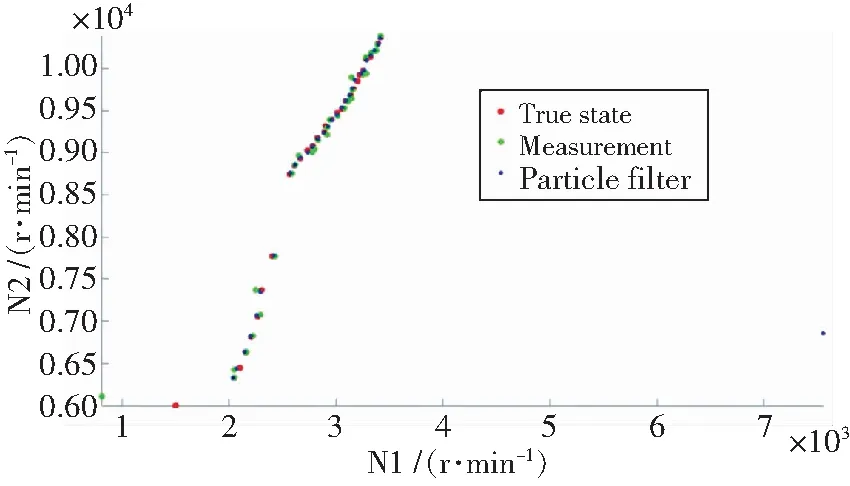
图2 粒子滤波估计结果Fig.2 Result estimated by PF

右侧的蓝线是由于初始时刻设定的粒子中心与初始转速之间的区别过大造成。具体偏差量如图3所示。可以看出在运行的最后一步，粒子分布和粒子中心的位置非常接近。

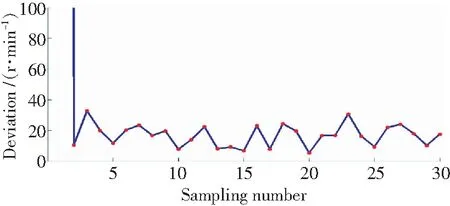
图3 粒子滤波估计结果偏差量Fig.3 Deviation of the result estimated by PF

3.2 故障信号检测

首先，以上述建立的涡扇发动机非线性模型为基础，设定燃油流量保持为100%，并在时刻将高压压气机效率从1降低到0.7，在时刻将高压压气机效率从0.7恢复到1。粒子滤波估计效果如图4所示。估计值与测量值、真实值的偏差量如图5所示。

图4 高压压气机效率突变时的粒子滤波估计结果Fig.4 Result estimated by PF for abruption of HPC

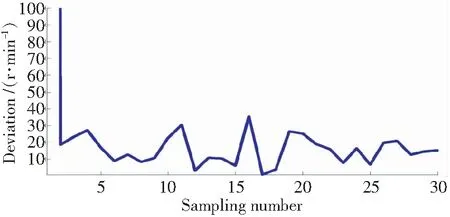
图5 高压压气机突变粒子滤波估计结果偏差量Fig.5 Deviation of the result estimated by PF

通过粒子滤波算法获得的估计值与实际测量值进行对比获得的估计残差量如图6所示。从图中可知，大致在第10采样点和第20采样点残差信号开始变化，并在第11、21采样点残差值远大于正常水平(超过正常水平的200倍以上)。这与设定在和时刻的高压压气机效率发生突变一致。在具体进行故障判断时，可以将阈值取为100，以尽可能地避免漏检和误检。

当突变较小，即保持燃油流量不变，使高压压气机效率在中间时刻从1变成0.98。估计值与实际测量值进行对比获得的残差量如图7所示。可以看出，残差信号发生了较为显著的变化，故障时刻对应的残差信号远大于正常水平，达到6倍左右。

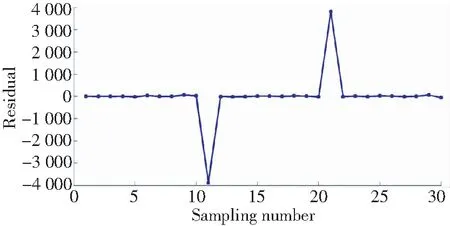
图6 压气机效率30%突变时故障残差信号Fig.6 Residual signal of 30% deviation of HPC’s efficiency

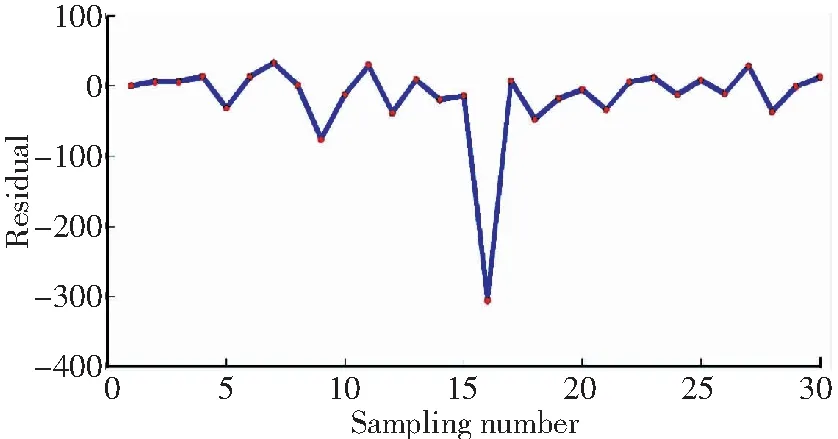
图7 压气机效率2%突变时残差信号Fig.7 Residual signal of 2% deviation of HPC’s efficiency

4 结论

1)采用粒子滤波方法，可以快速准确地获得非线性被控对象待估参数值。避免了卡尔曼滤波算法必须先获得线性模型的缺陷，也可以避免扩展卡尔曼滤波方法必须不断线性化的缺点。

2)在进行发动机健康诊断时，粒子滤波算法可以较好地检测到微小突变的发生。即使压气机效率值发生2%的退化时，残差信号依然会表现出较大差异(6倍以上变化)；当发生更为显著的故障(压气机效率突变30%)，残差信号具体值能达到正常水平的1 000倍以上，可以明显地检测到故障及故障发生时刻。

3)该方法推广到航空发动机健康监视与诊断领域，所生成的残差外加一系列逻辑判断可以达到有效区分故障、退化与发动机失效的效果。

[1] 黄金泉,冯敏,鲁峰. 基于自适应粒子滤波的涡扇发动机故障诊断[J]. 航空动力学报,2014,29(6):1498-1504.

[2] 鲁峰,黄金泉,孔祥天. 涡扇发动机故障诊断的快速原型设计[J]. 航空动力学报,2012,27(2):431-437.

[3] 杨欣毅,沈伟,王永华,等. 涡扇发动机气路部件衰退对转速差影响研究[J]. 推进技术,2014,35(5):610-617.

[4] 李丽敏. 统计聚类和粒子滤波在故障诊断中的应用研究[D]. 西安:西北工业大学,2014:83-84.

[5] 夏克寒,许化龙,张朴睿. 粒子滤波的关键技术及应用[J]. 电光与控制,2005,12(6):1-4.

[6] 梁军. 粒子滤波算法及其应用研究[D]. 哈尔滨:哈尔滨工业大学,2009:1-6.

[7] Andrieu C, Doucet A, Singh S S, et al. Particle methods for change detection, system identification, and control[J]. Proceedings of the IEEE,2004,92(3):423-438.

[8] 陈志敏,薄煜明,吴盘龙,等. 基于新型粒子群优化粒子滤波的故障诊断方法[J]. 计算机应用,2012,32(2):432-435.

[9] 刘志仓. 基于粒子滤波的非线性系统故障诊断与预测方法研究[D]. 西安:西安电子科技大学,2013:37-39.

[10] Chen M Z. Particle filtering based fault prediction of nonlinear systems [C]//IFAC Symposium Proceedings of Safe Process，2003.

[11] 胡昌华,张琪,乔玉坤. 强跟踪粒子滤波算法及其在故障预报中的应用[J]. Acta Automatica Sinica,2008,34(12):1522-1528.

[12] 樊思齐. 航空发动机控制[M]. 西安:西北工业大学出版社,2008:113-117.

[13] 王永华,杨欣毅,李本威,等. 基于免疫粒子群算法的涡扇发动机性能仿真[J]. 机械工程学报,2013,49(12):153-160.

Turbofan Engine Fault Diagnosis using Particle Filter Technique

YANG Bei，ZHANG Chen-yu

(SchoolofAircraftEngineering，NanchangHangkongUniversity,Nanchang330063,China)

A method of fault diagnosis without linear models for turbofan engine based on particle filter has been designed. Firstly, the value of particular parameters from sensors that contain noise and affected by disturbance would be estimated. Then, set threshold and construct residual signal from the estimated parameters and measured value according to the characteristic of particle filter. Simulation shows that the 30% deviation of HPC’s efficiency will lead to the change of 100 000% for residual signal. 2% deviation of HPC’s efficiency would lead to 600% change of the residual signal, and the change of residual’s change could be used to determine the degree of degeneration. The residual based on particle filter could distinguish degeneration from faults to achieve the objective of fault diagnosis.

particle filter; residual; turbofan engine; fault diagnosis; nonlinear model

2016年9月20日

2016年10月30日

航空科学基金(2014ZB56002)

杨蓓(1979年-)，女，硕士，讲师，主要从事发动机控制等方面的研究。

V233.7

A

10.3969/j.issn.1673-6214.2016.06.002

1673-6214(2016)06-0340-04