基于色差空间的低复杂度Bayer图像插值算法

赵亮 张宇烽 黄长宁



基于色差空间的低复杂度Bayer图像插值算法

赵亮 张宇烽 黄长宁

（北京空间机电研究所，北京100094）

覆盖在传感器表面的彩色滤波阵列(CFA)是CCD/CMOS传感器相机获取图像信息的关键，经过CFA 后每个像素点只能获得红、绿、蓝三种颜色中的一种颜色分量。另外缺少的两种颜色分量，需要通过周围像素的值进行插值获得。针对现有插值方法出现的复杂度高、插值还原图像颜色失真和边缘拉链效应问题，设计了一种基于色差空间的低复杂度Bayer图像插值算法。第一步利用5×5模板内的像素值判断插值方向，并用颜色之间的相关性插值获得绿色分量。在分析红、绿、蓝三种颜色相关性的基础上，利用色差原理，先恢复出缺失的绿色分量，再利用恢复出的绿色分量的高频部分替换红（蓝）分量的办法，插值缺失的蓝色和红色分量。利用Matlab程序，对5幅标准测试图和CE5T1试验飞行器自主相机拍摄的图片进行了仿真实验，比较了现有几种插值算法的复杂度和PSNR值。结果显示，文章提出的算法在主观视觉和客观评价方面都具有良好的表现。同时，算法复杂度低，适合硬件实现和图像的实时处理。

贝尔图像 颜色插值 双线性插值 峰值信噪比 航天遥感

0 引言

近年来，在图像传感器领域，数字彩色CCD和CMOS都备受关注且应用广泛。通常，数码相机传感器表面都涂覆着一层彩色滤波阵列（Color Filter Array，CFA）[1]。它的功能是使通过每个滤色单元的全色光仅允许红、绿、蓝三种颜色中一种颜色分量的光通过，所以输出图像中每个像素仅有一种颜色分量被记录下来。因此，要用颜色插值方法来恢复出该像素位置缺失的其余两种颜色分量，这个过程就称作CFA插值。一般经CCD和CMOS图像传感器产生的滤色图像与马赛克十分类似，因此也称彩色图像CFA插值过程为彩色图像的去马赛克化（Demosaicing）。

彩色滤波阵列通常有四种排列形式，目前所用的主流排列方式为Bayer阵列[2]。图1给出了一个5×5（单位：像素，全文同）的Bayer阵列模板，由图中可以看到各个像素格只有一种颜色分量。以24为例，代表蓝色通道的光强度，也称作蓝色通道的灰度值（为绿色通道的光强度，为红色通道的光强度，下同），2代表行号第二行，4代表列号第四列。因为人眼对可见光波段最为敏感，而其正好对应着绿色光谱成分[3-4]，所以绿色像素的采样样本更多。从图1可看到，绿色像素占了全部的二分之一，绿色像素被称作亮度因子（Luminance），红色和蓝色像素各占Bayer阵列的四分之一，它们被称为色度因子（Chrominance）[5]。当数码相机采集完一幅图像以后，会对它按步骤进行一系列的图像处理[6]，有自动白平衡、黑电平校正和图像增强处理等，而CFA彩色图像插值是整个处理环的第一步。

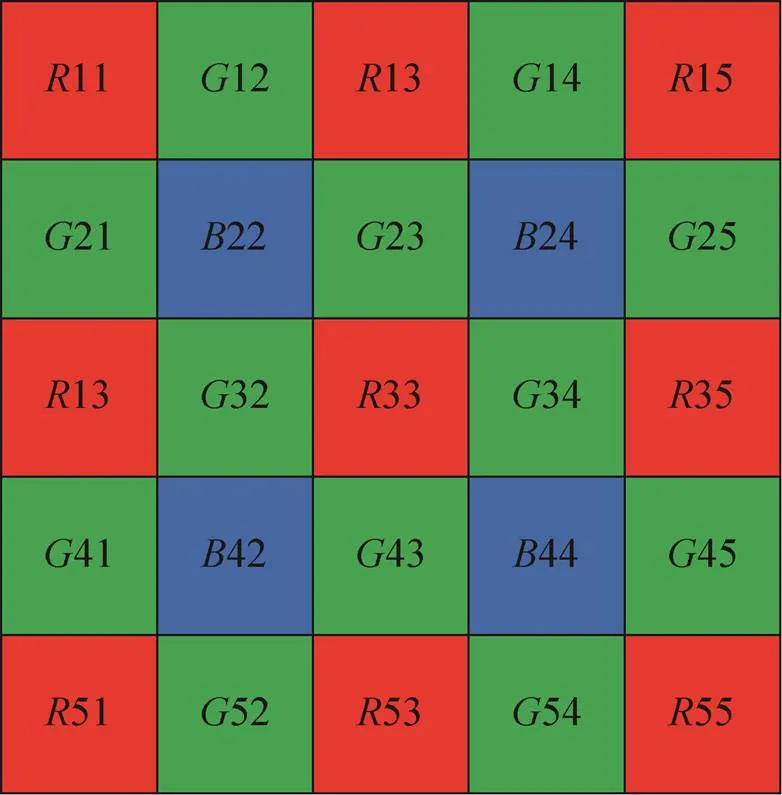
图1 5×5 Bayer彩色滤波阵列

众多学者对颜色插值方法进行了大量研究。文献[7]提出了Mondfiaan的彩色图像信息模型，根据这一模型，在一幅图像的平滑区域，各颜色分量有着恒定的比值而几乎不怎么变化，在此基础上衍生出很多颜色比空间的插值算法，如文献[8]；文献[9]提出在颜色差空间进行线性插值的算法；文献[10]在颜色差空间利用有理函数插值的方法恢复彩色图像；文献[11]提出在通常用于影片连续处理的YCbCr的颜色空间进行插值的方法恢复图像。在上述算法中，颜色失真、边缘拉链效应和图像模糊都有不同程度的体现，且这些算法包含着相对复杂的乘除等运算，会消耗大量的硬件资源。

本文根据红、绿、蓝三种颜色间的关联性，基于色差梯度原理，参考了Bayer图像的自适应插值算法，提出一种新的彩色图像插值算法，没有复杂的乘除法运算，该算法复杂度低，满足实时图像处理的要求。同时能够有效改善图像品质，减少颜色失真，避免拉链效应的产生。

1 基于色差梯度的Bayer图像插值算法

首先通过梯度判断恢复出缺失的绿色分量，之后利用恢复的绿色分量和原有绿色分量恢复缺失的红色和蓝色分量，在恢复红色和蓝色分量的过程中，同样进行了梯度判断。

本文算法建立于图像的颜色通道相关性基础上。图像的颜色相关性指在光强变化方面，图像的三种颜色通道具有一定的关联性和相似性，一般用色比规律和色差规律来表示。根据色比规律，对于同一平滑区域内的相邻两个像素点（,）和（,），其三个颜色通道的光强比近似相等，即：

式中（,）、（,）、（,）分别为像素点（,）处红色、绿色、蓝色通道的光强；（,）、（,）、（,）分别为像素点（）处红色、绿色、蓝色通道的光强。

与色比规律类似，色差规律认为相邻像素点的三个颜色通道间的光强差近似相等，即：

颜色通道间的相关性可由下式来计算[12]：

式中分别代表两种不同颜色分量；代表图像尺寸；（,）（）分别代表该颜色分量在对应位置处的灰度值；μ，μ代表相应颜色分量的灰度均值。

为了进一步说明各颜色通道之间的相关性，本文将原始彩色图像分别提取为红色、绿色、蓝色分量的灰度图（图2）。显然，观察变换为各颜色分量的灰度图像，依然能清晰地分辨出人物背景等各个细节和边缘，在平滑区域内三者总体变化一致，只是各颜色分量强度不一样。换言之，三个颜色分量的图像边界区域（高频信息）和背景（低频信息）类似。这也说明了各颜色通道之间具有很强的相关性。

（a）彩色图像 （b）红色分量 （c）绿色分量 （d）蓝色分量

（a）Color image （b）Red channel image （c）Green channel image （d）Blue channel image

图2 彩色和单颜色分量图像

Fig.2 RGB color image and three color channels’ images

图3分别给出了R-G、B-G颜色通道的色差信息，可以看到，两张色差图与图2所示的各单通道图亮度明显降低，说明各通道之间光强接近；同时，色差图像的细节较各单通道分量信息损失严重，但还能大致反映原始图像的轮廓，说明各颜色通道有着相似的强度变化趋势。

因此，结合图像颜色相关性和以上论证，提出用绿色分量来代替恢复出缺失的蓝色红色分量，最终得到一副完整的RGB图像。同时，由于减法运算比除法运算简单，并且在计算过程中不需要考虑分母为0的情况，因此采用色差规律来恢复彩色图像。

（a）红绿色差 （b）蓝绿色差

（a）Difference image between red and green （b）Difference image between blue and green

图3 色差图像

Fig.3 Image of color difference

1.1 绿色分量的恢复

在恢复绿色分量时，用到周围两个邻域内的像素，因此本文采用5×5模板恢复彩色图像，如图4所示，最中心位置标注为（,），其强度为（,），其余像素点的强度根据坐标标注。

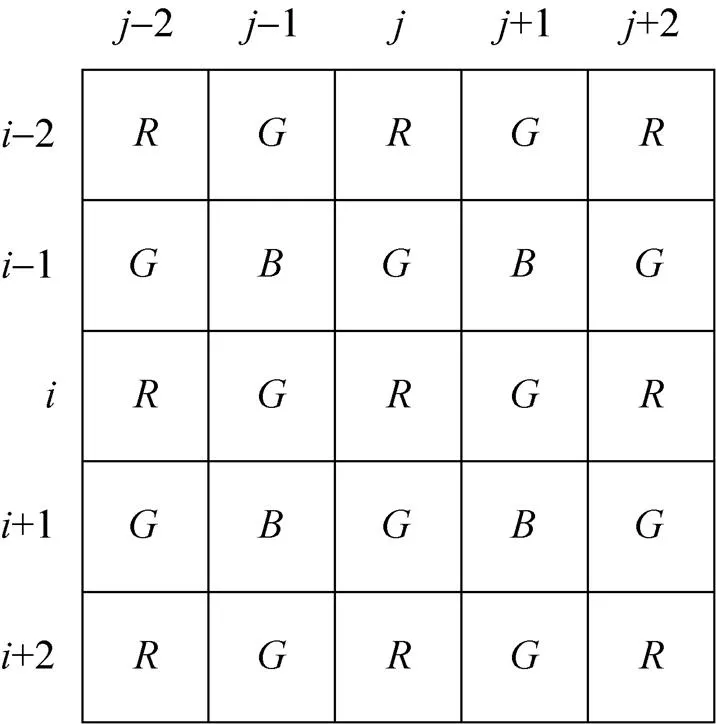
图4 5×5插值恢复绿色分量模板

在图像插值恢复的过程中，如果相邻像素值有较大的对比时，插值恢复的图像边缘部分会有明显的模糊和杂色失真，这是因为插值引入了邻域内不相关的像素，或者说是插值方向穿越了边缘，一经插值后，插值恢复的图像色调发生了改变，以致产生了错误像素。因此，要避免模糊和杂色，就应该尽可能顺着图像边缘方向进行插值，而不是横跨边缘。

对于插值跨越边缘问题的消除，需要通过计算方向算子来处理。一幅图像中的每个像素都有邻域，且与邻域内的其他像素存在不同程度的相关性。在恢复绿色分量时，引入梯度的概念，梯度即方向算子，它可以帮助判断是水平方向还是垂直方向的相关性更强。

在仅有红色分量的像素采样点处，恢复出绿色分量。参考图中的（,），计算出（,）；其水平和竖直方向的梯度分别为：

中心处（,）的计算方法为：

当Δ＜Δ时，

当Δ＞Δ时，

当Δ=Δ时，

式中 Δ为水平梯度；Δ为垂直梯度；（,）为图4中（,）恢复出的绿色分量。

同理，在仅包含蓝色分量的像素采样点处，其计算方法与上述过程相同。利用此方法，即可恢复出图片全部缺失的绿色分量。

1.2 红色分量、蓝色分量的恢复

红色分量的恢复需要绿色分量和红绿色差R，如式（9）所示。蓝色分量的恢复需要绿色分量和红绿色差B，如式（10）所示

式中（,）为（,）点的红色光强；（,）为（,）点的绿色光强；R（,）为（,）点的红绿色差。（,）为（,）点的红色光强；（,）为（,）点的绿色光强；（,）为（,）点的蓝绿色差。

以红色分量的恢复为例，若要恢复出（,），第一步求得红色和绿色色差R（,），第二步由（,）、R（,）相加就可插值得出（,）点的红色分量（,）。在1.1部分，已插值得到全部的绿色分量（,），因此求得红绿色差是恢复红色分量的关键。

以恢复红色分量为例。蓝色分量的恢复过程与红色分量的恢复过程一致，只是由变为了。

将已经恢复的全分量图像与原始贝尔图像数据做差，得到色差图像。5×5计算R，B模板如图5所示。图中，为红绿色差值；B为蓝绿色差值。

图5 5×5计算Rg、Bg模板

1）首先计算B位置上的红绿色差，由图5的颜色通道相对位置，有如图6所示的像素位置模型

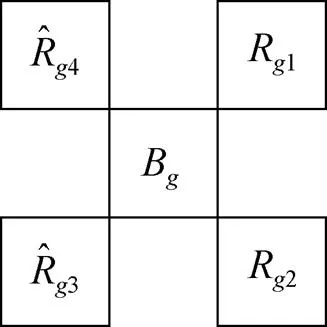
图6 3×3的红绿色差模板且中心像素为B

2）计算位置上的红绿色差，按照图7（a）所示像素位置模型计算，同时，由Bayer模板的红绿蓝排列方式，当中心像素为时，有两种情况，一种是左右都是（红行，如图6（b）），一种是左右都是（蓝行，如图6（c）），两种情况计算位置上的红绿色差方法有所不同，过程如下：先计算左右都是红色分量时的位置的红绿色差，如图6（b）所示。图7（a）中、、、为此模板内相邻位置的红绿色差值。

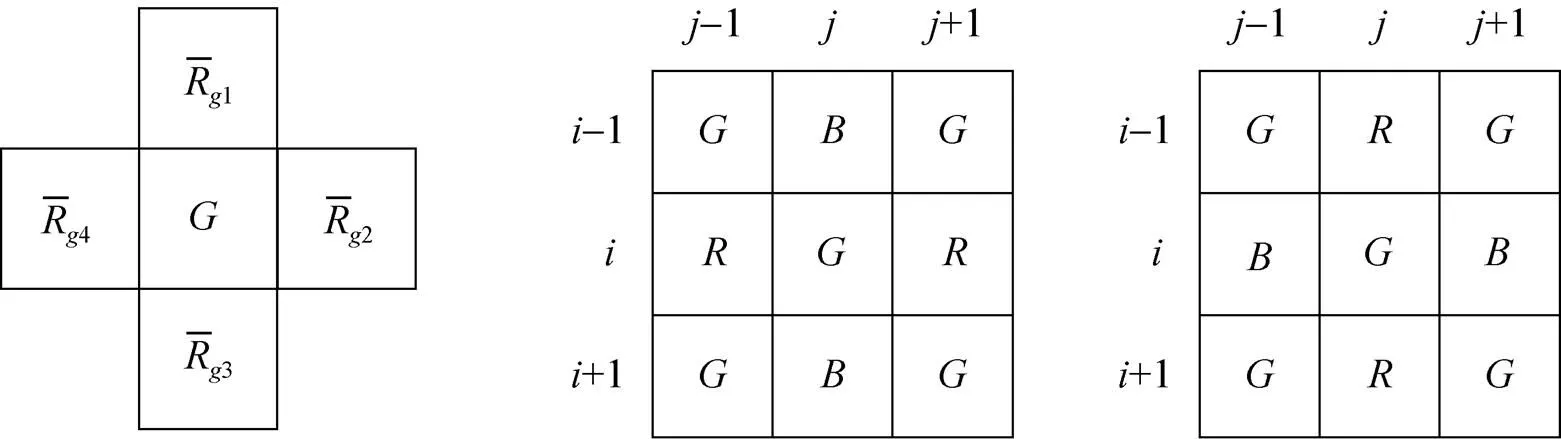
（a）3×3的红绿色差模板 （b）左右为红色 （c）左右为蓝色

（a）Red-green difference image pattern （b）Around(red row) pixel （c）Around(blue row) pixel

图7 中心像素为绿色分量时求取R

Fig.7 CalculatingRwhen the center pixel is green channel

当│(-1,+1)+(+1,+1)-(-1,-1)-(+1,-1)│＜│(+1,-1)+(+1,+1)-(-1,-1)-(-1,+1)│时，

当│(-1,+1)+(+1,+1)-(-1,-1)-(+1,-1)│≥│(+1,-1)+(+1,+1)-(-1,-1)-(-1,+1)│时，

3）与2）步骤类似，通过第一步水平方向上平滑得出的处的红绿色差，可以依式（14）得出（蓝行）上的红绿色差，如图7（a）所示。

当│(-1,+1)+(+1,+1)-(-1,-1)-(+1,-1)│＜│(+1,-1)+(+1,+1)-(-1,-1)-(-1,+1)│时，

当│(-1,+1)+(+1,+1)-(-1,-1)-(+1,-1)│≥│(+1,-1)+(+1,+1)-(-1,-1)-(-1,+1)│时，

4）通过上述步骤，可以得到位置和位置处的红绿色差R，结合2.1得到的全部绿色分量，就可恢复出缺失的红色分量，如式（16）所示，

使用与上述一样的步骤方法，就能恢复出缺失的蓝色分量，进而就插值恢复出一幅完整的RGB图像。

2 实验及结果分析

2.1 复杂度分析

评价算法复杂度[13-14]的参数主要由两个，一个是完成插值所需预缓存数据的行数，另一个是完成插值所需的加减、乘除、位移等运算步骤的次数。下文对本文提出的算法和其他五种插值算法—双线性插值法（BI）、色比恒定法（CCRI）、高效颜色插值（ECI）[15]、改进的高效颜色插值（EECI）[16]、低功耗高品质的颜色插值（LCI）[17]作复杂度分析和比较。

本文算法在恢复绿色分量时，用到了相邻的两个像素的数据，因此需预先缓存连续五行的像素数据。算法中涉及两次比较运算。因本文插值所用的Bayer图像中绿色像素数量占全部像素的二分之一，蓝色和红色像素数量分别占全部像素的四分之一，在插值恢复这些颜色时的运算次数也占与之一样的比例。

经统计，本文算法所需的加减运算次数为：

（（3++7）/4+（4+3）/4+（+2）/2+/2)×2=13

位移运算为：

（3/4+2/4+/2）×2=3.5

其中，、分别为图像的宽和高（单位：像素），表示整幅图像的像素个数。表1给出了六种算法的比较结果。

表1 六种插值方法的复杂度比较

Tab.1 Complexity comparison of six demosacing methods (image size M×N)

由表中数据看出，BI算法复杂度是最低的；ECI和EECI算法都需更多的缓存数据，同时EECI的加减和乘除的次数都远远大于其他算法，它是六中算法中复杂度最高的；本文算法比LCI算法需多缓存两行数据，但是相比LCI需要多次乘除，本文算法没有乘除运算，两种方法加减次数也接近；因此，综合来看，本文算法复杂度与LCI复杂度最接近，不包含复杂的运算步骤，方便硬件实现。

2.2 图像质量分析

通过Matlab仿真验证，使用国际上插值算法研究人员常用的5幅柯达标准BMP彩色图像和“嫦娥五号”试验飞行器(CE5T1)拍摄的“地球”作为测试图，这些测试图色彩丰富，细节变化多，图像左下角标有图序，用数字1-6代表各幅图片，如图8所示。之后对测试图的Bayer模板分别运用BI、CCRI、ECI、EECI、LCI和本文算法将Bayer图像进行了彩色插值，恢复成为彩色图像。采用主观观察和峰值信噪比（Peak Signal to Noise Ratio，PSNR，单位dB）[18-19]进行评估图像质量。PSNR能够反映处理后图像与原图像的吻合程度。如表2，给出了包括本文算法在内的6种插值算法恢复出的图像的PSNR值。

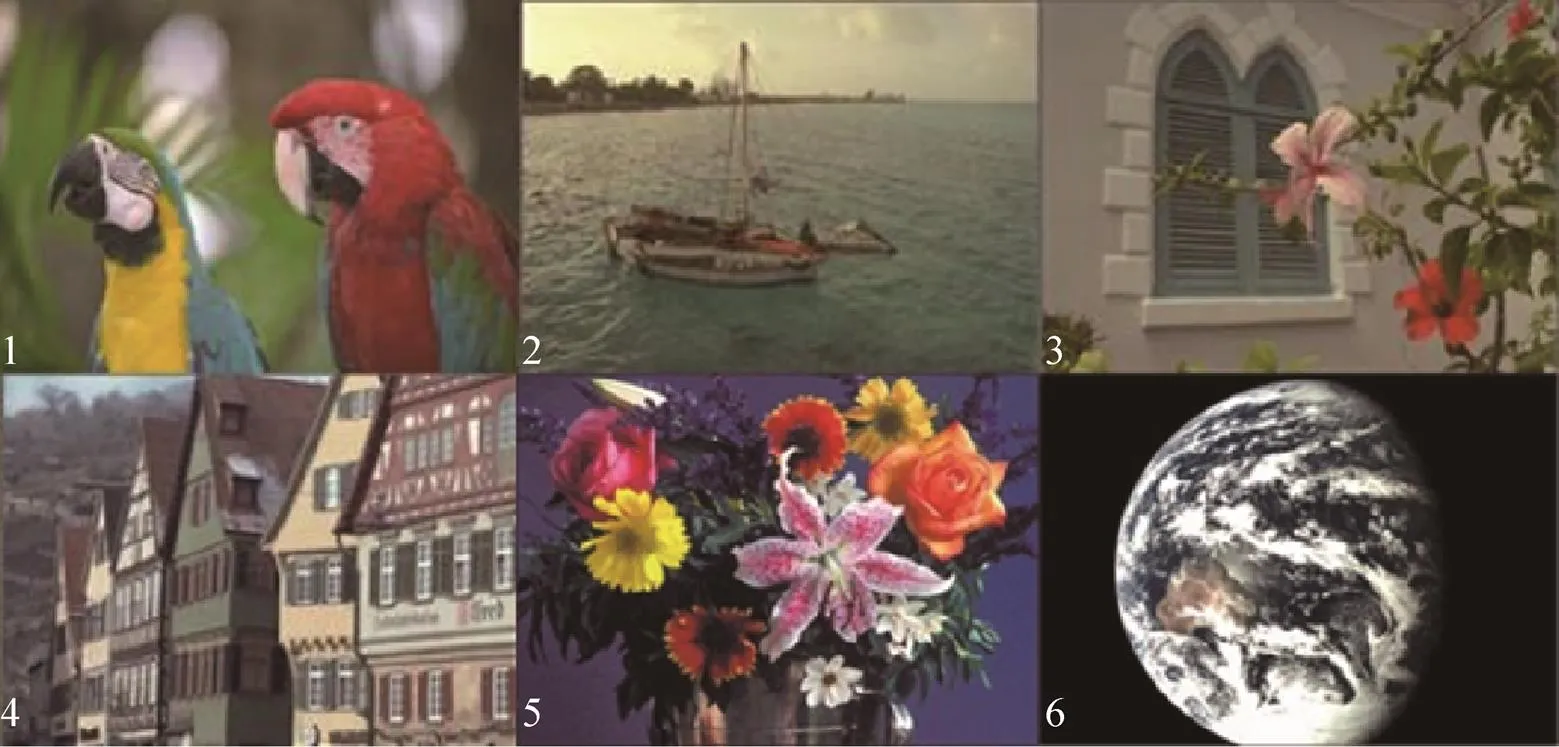
图8 测试用图像

表2 六种插值算法恢复的图像各颜色通道的PSNR值比较

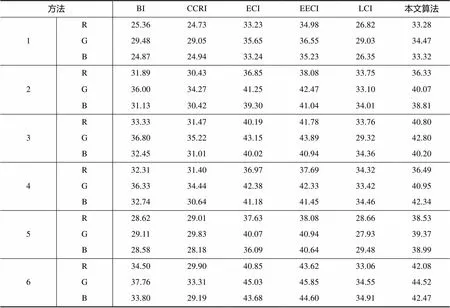
Tab.2 PSNR comparison of the 6 reconstructive images by six demosaicing methods 单位：dB

由表中数据可以看出，三种算法中，红色分量和蓝色分量的PSNR值明显低于绿色分量的PSNR值，这是由Bayer阵列三种颜色分量各自所占的比例决定的，红色和蓝色分量更少，失真更严重。

从6幅图像的PSNR值来看，BI、CCRI与LCI获取的插值图像的PSNR较低，也是最接近的。其中LCI插值恢复图像红蓝色分量PSNR值略高于BI和CCRI，而图像绿色分量PSNR值却比BI、CCRI低了2-3dB。这是因为LCI恢复的绿色分量建立在红蓝分量的恢复基础上，而红蓝分量像质本身很低，因此恢复的绿色分量损失严重。

ECI、EECI和本文算法是六种插值算法中插值恢复出的图像的PSNR值是最高的，获取的像质也最好。本文算法恢复出的图像PSNR比BI、CCRI、LCI高6~7dB，和ECI接近，比EECI低1~2dB。

结合复杂度分析结论，与本文算法复杂度最接近的是LCI，但其PSNR值远低于本章算法恢复出的图像；与本文算法PSNR值相近的是ECI、EECI，但其复杂度提升不少，包含了更多的缓存数据行和大量的乘除运算。

在6幅测试图中，5号测试图色彩更加丰富，边缘变化更多，便于主观观察插值恢复的图像。在下图8中，给出了5号测试图几种插值算法恢复出的彩色图像的实际效果图和贝尔图像。图9给出了几种插值算法恢复出的彩色图像的局部放大图。表3为插值恢复出5号测试图各种算法所消耗的时间（），反映了算法的效率。

图9 5号测试图的Bayer原图及六种插值方法处理结果

图10 六种插值方法的局部细节放大对比

表3 插值恢复出5号测试图各种算法所需时间

Tab.3 Run time of 5th reconstructive image by six interpolation methods

从实际插值恢复的图像效果来看，图9中（a）、（b）、（e）恢复出的图像金属桶线出现了明显伪彩色，且花朵纹理模糊，（c）、（d）、（f）三种方法恢复的图像考虑了颜色通道之间的相关性，改善了图像质量，几乎观察不到伪彩色，而图10中（d）、（f）中的花瓣纹理比（c）中的稍稍清晰。因此本文算法插值恢复出的效果与ECI、EECI类似，同时从表3看出，ECI算法时间是本文算法时间的1.5倍，而EECI是本文算法的近2.5倍。

综上所述，本文算法在控制了复杂度的情况下，牺牲时间代价最小，获得了像质的最大提升。同时本文算法获取的图像PSNR值较高，所付出的处理时间代价是值得的。

3 结束语

本文在研究现有各种彩色图像插值算法的基础上，结合彩色图像中红色、蓝色、绿色分量之间的耦合性，提出了一种基于梯度和色差的空间彩色插值算法。这种算法运行能够有效避免图像颜色失真和拉链效应的产生，所恢复出的图像纹理清晰，信噪比高，视觉效果良好。同时，算法没有复杂的乘除运算，只有简单的加减运算，复杂度低，在运算时间相对较短的情况下可获得良好的插值图像，综合考虑算法插值后图像的品质、算法速度效率和硬件的可实行性，本文算法更能胜任彩色图像插值工作。

[1] LUKACR, PLATANIOTIS KN. Color Filter Array: Design and Performance Analysis[J]. IEEE Transactions on Consumer Electronics, 2005, 51(4): 1260-1267.

[2] BAYER B E. Color Imaging Array: US 3971065[P]. 1976-07.

[3] RAMANATHR, SNYDER W E, BILBRO G L. Demosaicking Methods for Bayer Color Arrays[J]. Journal of Electronic Imaging.2002, 11(3): 306-315.

[4] ZHANG L, WU X. Color Demosaicking via Directional Linear Minimum Mean Square Error Estimation[J]. IEEE Computer Society, 2005, 14(12): 2167-2178．

[5] LI X, Gumurk B, ZHANG L. Image Descalcing: a Systematic Survey[C]. Proc. SPIE 6822, Visual Communications and Image Processing 2008, 68221J. DOI: 10.1117/12.766768.

[6] 满溢云, 胡永力, 王小勇. 从图像处理的角度观点出发来看光学遥感器的成像质量[J]. 航天返回与遥感, 2006, 27(1): 18-22. MAN Yiyun, HU Yongli, WANG Xiaoyong. From Image Processing Concepts to Glom the Image Quality of Optical Remote Sensor[J]. Spacecraft Recovery & Remote Sensing, 2006, 27(1): 18-22.

[7] ELIASON P T, SODERBLOM L A, CHAVEZ P S. Extraction of Topographic and Spectral Albedo Information from Multi Spectral Images[J]. Photogramm Engineering Remote Sensing, 1981, 48(11): 1571-1579．

[8] COK D R. Reconstruction of CCD Images Using Template Matching[C]. International Science and Technology (IS&T)’. 47th Annual Conference／International Congress on Imaging Science (ICPS), Rochester NJ USA, 1994: 380-385.

[9] PEISC, TAM I K. Effective Color Interpolation in CCD Color Filter Array Using Signal Correlation[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2003, 13(6): 503-513.

[10] 刘晓松, 杨新, 汪进, 等. 一种用于数字图像传感器的彩色插值算法[J]. 中国图像图形学报, 2003, 8(5): 516-521．LIU Xiaosong, YANG Xin, WANG Jin, et al. A kind of Color Interpolation Algorithm for Digital Image Sensor[J]. Journal of Image and Graphic, 2003, 8(5): 516-521．

[11] 喻再光, 赵群飞. 基于Ycbcr三基色插值及其在DSP上的实现[J]. 计算机工程与应用, 2005, 8(10): 104-106. YU Zaiguang, ZHAO Qunfei. Three-color Interpolation Algorithm Based on Ycbcr and Its Implementation on a DSP System[J]. Computer Engineering and Application, 2005, 8(10): 104-106.

[12] GUNTURK BK, YUCEL A, RUSSELL M. Mersereau Color Plane Interpolation Using Alternating Projections[J]. IEEE Transaction on Image Processing, 2002, 11(9): 997-1013.

[13] 周婷. 贝尔图像自适应插值算法研究[D]. 太原: 太原理工大学, 2011. ZHOU Ting. Adaptive Demosaicing Algorithms Based on Bayer Color Filter Array[D]. Taiyuan: Taiyuan University of Technology, 2011.

[14] 张起贵, 赵丽娟. 基于FPGA的贝尔图像插值算法实现[J]. 科学技术与工程, 2012, 12(35): 9568-9569. ZHANG Qi gui, ZHAO Li juan. Research on Interpolation Algorithm Based on FPGA[J]. Science Technology and Engineering, 2012, 12(35): 9568-9569.

[15] PEI S C, TAM I K. Effective Color Interpolation in CCD Color Filter Arrays Using Signal Correlation[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2003, 13(6): 503-513.

[16] CHANG L, TAN Y P. Effective Use of Spatial and Spectral Correlations for Color Filter Array Demosaicing[J]. IEEE Transactions on Consumer Electronics, 2004, 50(1): 355-365.

[17] HSIA S C, CHEN M H, TSAI P S. VLSI Implementation of Low-power High-quality Color Interpolation Processor for CCD Camera[J]. IEEE Transactions on Very Large Scale Integration Systems, 2006, 14(4): 612-625.

[18] SONJA G, MISLAV G, MARTA M. Reliability of Objective Picture Quality Measures[J]. Journal of Electrical Engineering, 2004, 55(1): 3-10.

[19] MARIA V. Test Image Quality[D]. Lappeenranta: Lappeenranta University of Technology, Department of Information Technology, 2004.

A Low Complexity Interpolation Algorithm for Bayer Image Based on Color Difference Space

ZHAO Liang ZHANG Yufeng HUANG Changning

（Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）

A single CCD/CMOS sensor camera to capture image is based on the Color Filter Array covered on the sensor, when the light pass through the CFA, each pixel can get only one color component of three-primary colors(red, green, blue). In order to recover the other two missing color components ,they must be obtained by interpolation. Focusing on the complexity of the existing interpolation methods, color distortion and zipper effect of the interpolation image, this paper designs a low Complexity Interpolation Algorithm for Bayer Image Based on Color Difference Space. The first step is to estimate interpolation direction taking advantage of the pixels in 5×5 template and use the correlations between green and red or between green and blue to interpolate green components. Based on the analysis of the frequency correlations between color components and by using the color difference principle, we use the high frequency part of the green component to interpolate to get the missed red and blue components. Through Matlab we carry out simulation experiments based on the images captured by our CE5T1 camera, and compare several existing interpolation algorithms with the proposed algorithm. The results show that the proposed algorithm performs well both in visual and numerical aspects. At the same time the proposed algorithm has a low complexity, suitable for hardware implementation and image real-time processing.

bayerimage; color interpolation; bilinear interpolation; peak signal to noise ratio; space remote sensing

（编辑：毛建杰）

TP751.1

A

1009-8518(2016)03-0128-11

10.3969/j.issn.1009-8518.2016.03.015

赵亮，男，1990年生，2016年获中国空间技术研究院光学工程专业硕士学位。研究方向为遥感图像处理。E-mail：zl_allany@163.com

2016-03-04

国家重大科技专项工程