盘缝带伞超声速开伞过程研究

杨璐瑜张红英陆伟伟童明波



盘缝带伞超声速开伞过程研究

杨璐瑜张红英陆伟伟童明波

（南京航空航天大学飞行器先进设计技术国防重点学科实验室，南京210016）

随着深空探测着陆的发展，对降落伞超声速开伞的研究迫在眉睫。文章采用守恒元/解元算法对美国某空投试验所用盘缝带伞进行超声速开伞过程的仿真模拟，将数值仿真得到的伞衣充满外形和最大开伞动载与此盘缝带伞的高空投放试验进行对比，获得较为一致的结果，验证了数学模型的可靠性。在此基础上，继续对此盘缝带伞超声速开伞过程进行详细研究，分析了开伞过程伞衣充气外形变化、开伞动载变化、伞衣应力分布以及伞衣不同位置的应力随时间的变化情况。结果表明，开伞过程中伞衣会存在一定的“呼吸”现象，同时在伞衣口处会形成一道弓形激波。开伞动载在经历了较大的波动后逐渐稳定，伞衣盘上的应力比伞衣带上的应力值大。因此，在盘缝带伞的设计中应着重考虑伞衣盘部分的强度要求。

盘缝带伞 充气 超声速 守恒元/解元算法 探测着陆

0 引言

20世纪60年代，美国从“海盗号”计划开始，对火星探测用伞开展了大量的研究[1-3]，并选定了盘缝带伞作为火星探测用伞。但在当时，这些研究以高空投放试验和风洞试验[4-5]为主。后来随着“火星探路者”[6]、“火星漫游者”[7-8]、“火星科学实验室”[9-11]等火星计划的陆续开展以及计算机技术的飞速发展，采用数值模拟方法[12-14]分析降落伞超声速下的开伞过程也越来越受到重视。文献[15]对空投试验结果进行了仿真分析，评估了仿真模拟的功能和试验降落伞模型的局限性。但是作者为了得到仿真模拟与飞行试验第一次开伞动载的对比，将阻力系数作为仿真输入参数。文献[16]基于LS-DYNA结构分析仿真软件中的任意拉格朗日欧拉（Arbitrary Lagrange Euler，ALE）算法仿真评价了两种盘缝带伞在亚声速、跨声速和超声速下的开伞过程。文献[17]也使用了LS-DYNA软件中的ALE方法模拟了=1.5条件下降落伞的流固耦合过程，更详细地分析了降落伞在超声速气流中的开伞情况，并将伞衣透气性也作为了模拟输入参数。但是，ALE方法在超声速计算中存在计算量过于庞大的问题，对计算资源的要求很高，而且容易出现计算发散。

超声速流动对降落伞性能的影响是深远的，目前超声速开伞过程的流固耦合计算除了传统的计算流体力学（Computational Fluid Dynamics，CFD）求解器和控制仿真动力学（Control Simulation Dynamics，CSD）求解器松散耦合方法（该方法不仅工作量大，计算精度也难以保证，故不建议选择）以外，主要采用基于LS-DYNA软件的ALE方法和守恒元/解元方法（Conservation Element and Solution Element Method，CE/SE）。研究表明，虽然两种方法都可用于超声速开伞的流固耦合计算，但是超声速条件下，ALE方法计算耗时长、难收敛，并且往往得不到正确的结果，还可能出现计算终止，即ALE方法更适用于计算亚声速。而CE/SE方法在计算超声速开伞时虽然仍然存在较多的限制因素和较大的计算难度，但相比于ALE方法，CE/SE方法更适用于计算超声速。尽管美国进行了大量的试验研究，但在数值仿真计算[18-19]方面，公开的文献并不多，更没有系统性的概述和阐释。要想从根本上进行探索，对超声速开伞进行专门研究是非常必要的。

本文选用美国某一高空投放开伞试验使用的盘缝带伞[20]进行了超声速（=1.59）开伞仿真模拟，基于LS-DYNA中的CE/SE算法研究降落伞在模拟火星大气环境下的开伞过程。为了验证仿真计算的可靠性，对比了仿真计算与试验的最大开伞动载和充满时的投影面积变化。在此基础上，继续对盘缝带伞超声速开伞过程进行详细研究，分析了开伞过程伞衣充气外形变化、开伞动载变化、伞衣应力分布以及伞衣不同位置的应力随时间的变化情况，仿真结果可为火星探测降落伞设计提供参考。

1 仿真模型建立

降落伞仿真模型选用的是美国某一高空投放试验模拟火星大气环境下开伞所使用的盘缝带伞， 命名为M伞。仿真所用的降落伞构型为伞衣盘顶部开孔，伞绳采用一体式连续设计，从顶孔中心汇 交点处沿伞衣径向穿过伞衣盘接缝和伞衣缝，通过伞衣带接缝延伸至伞绳汇交点后，再按与前面相 反的顺序返回至顶孔中心处。顶孔周向、伞衣盘周向及伞带周向均使用加强带加固。具体几何参数如表1所示。

由于超声速开伞仿真计算工作量庞大，而本文重点在于对工程应用中所关心的开伞动载和伞衣充满外形进行研究。为了节省计算时间，计算时降落伞结构单元以一定的初始外形作为起始状态，计算初始伞衣的几何模型如图1所示。

表1 M伞几何参数表

Tab.1 Geometrical parameters of M

图1 降落伞几何模型

流场仿真模型选用的是圆柱形流场，其基本尺寸为：流场半径f= 49m，流场长度f= 75m。流场下端距伞绳汇交点距离大致为4m，流场上端距离伞衣盘面为50m。本文采用CAD三维建模技术并参考美国的仿真建模方法，绘制出降落伞的初始外形和流场的外形。

本文使用Hypermesh有限元软件对降落伞和流场的几何模型进行分块并划分有限单元网格。降落伞的单元属性为：伞衣采用壳单元（shell），个数为1.7×104，伞绳和加强带采用离散的梁单元（beam），个数为7.1×103。流场有7.5×105个六面体固体单元（solid）。流场和降落伞的有限元网格模型如图2所示。

将处理好的有限元模型导入LS-DYNA软件进行前处理，并对流场有限元模型作了以下假设：

1）流场为可压非定常流场，符合N-S方程；

2）流场模型中流体的速度方向恒定，速度由定义的速度曲线进行加载；

3）流场模型的壁面均设置为无反射边界条件。

2 仿真结果与空投试验对比分析

由于测试设备的欠缺，当时空投试验的数据反馈并不完整，无法直接进行降落伞阻力系数等数据的对比，因此选择了投影面积和开伞动载这两项指标进行对比分析，对比结果反映出仿真数据与空投试验数据吻合得较好。

2.1 投影面积对比

将研究的盘缝带伞的空投试验所测得的稳定展开后的投影面积和此伞数值仿真得到的稳定展开后的投影面积数据进行对比分析。空投试验降落伞稳定展开后的投影面积为π×2/4 = 88.24m2（其中直径= 10.6m），数值仿真计算降落伞稳定展开后的投影直径为10.59m。可见，数值仿真计算的伞衣充满投影面积跟空投试验结果基本相符。本文还选取降落伞完全充满前后的时间段作研究（9.8~10.8s），分析空投试验与数值仿真计算的降落伞投影面积的变化情况，并给出如图3所示的降落伞投影面积率（降落伞某一时刻的投影面积与降落伞理想状态下完全充满的投影面积的比值）的对比曲线。由图可见，在降落伞完全充满前后的这1s时间内，伞衣投影面积先减小再增大，最后基本稳定（降落伞伞衣呈现充满时刻的“呼吸”现象）。但从变化值来看，投影面积波动不明显，说明“呼吸”现象不明显，这与盘缝带伞的结构有关，由于结构透气量大于平面圆形伞，所以充满时的“呼吸”现象没平面圆形伞明显。从曲线可看出，无论是投影面积变化趋势，还是投影面积率，仿真计算与试验所测数据均吻合得较好。

图3 投影面积率对比

2.2 开伞动载对比

此盘缝带伞高空投放试验的最大动载值为69kN，而数值仿真所得到的最大动载为78.5kN，相对误差大概为13.77%。由于空投试验时降落伞是有限质量开伞，而本仿真计算采取的是无限质量开伞，空投试验在降落伞充气过程中伞系统速度减小，所以开伞动载低于无限质量开伞。因此该差异是合 理的。

3 降落伞开伞过程的仿真结果及分析

3.1 充气过程伞衣外形变化和开伞动载变化分析

本文通过使用LS-DYNA软件完成了对此盘缝带伞开伞过程的动态仿真，实现了降落伞开伞过程的可视化动态模拟，截取10个时间点的伞衣充气外形，如图4所示，并且获得了整个充气过程中降落伞开伞动载的变化过程，见图5。

从图4可以看出，由于初始外形为不考虑折叠的理想外形，整个充气过程持续时间较短，伞衣形状波动较为平缓，在0.3s后基本达到最终稳定展开时的充满外形。虽然在0.18s以后，伞衣充气外形变化不大，但还是有细微的伞衣振荡现象，随着时间的增长，伞带部分展开得越完全，但并不是始终稳定在一个外形。

由图5可直观看出数值仿真中开伞动载在降落伞的整个充气过程中经历了较大的波动：随着伞衣逐渐充开，开伞动载逐渐增大，在达到过充气阶段后，伞衣有一定的收缩，开伞动载降低，随后降落伞在恒定的来流速度下重新充满至稳定外形，开伞动载也升高至稳定值，最终阻力稳定在48kN左右。

3.2 流场分析

分别在CFD-FASTRAN计算流体动力学软件和LS-DYNA结构分析软件中进行流场仿真计算，得到流场压力和速度分布如图6~7所示。

通过对比流场压力云图可知，由于盘缝带伞伞衣结构的影响，在伞顶孔和伞衣缝处存在一个低压区，这是因为流过伞顶孔和伞衣缝的气流流速较大。而伞衣口和伞衣内部处于高压区，并且在伞衣口处形成一道弓形激波，由于马赫数并不大，激波角大概为70°左右。

（a）CFD-FASTRAN流场压力云图 （b）LS-DYNA流场压力云图

（a）Fluid pressure from CFD-FASTRAN （b）Fluid pressure from LS-DYNA

图6 流场压力云图对比

Fig.6 Comparison of fluid pressure

（a）CFD-FASTRAN流场速度云图 （b）LS-DYNA流场速度云图

（a）Fluid velocity from CFD-FASTRAN （b）Fluid velocity from LS-DYNA

图7 流场速度云图对比

Fig.7 Comparison of fluid velocity

通过对比流场速度云图可知，在伞壁面内部由于壁面对气流的阻挡，气流速度明显下降。比较图 7（a）和图7（b）的流场云图可以看出两者的速度分布及激波位置近似一致，但流固耦合计算中由于流场单元较少，因此其结果对于激波和尾流的捕捉相对较为粗糙，而若是加密流场单元网格将会导致计算时间成倍的增加，这给原本就有所限制的计算资源带来了更大的负担。

尽管两者流场图有一定差别：LS-DYNA软件计算得到的速度流场图未能呈现伞顶孔后方的高速流动，但是总体上，压力和速度分布最大值差别不大，压力和速度分布区域也大致相同。

3.3 伞衣各点应力变化

图8给出了数值仿真计算得到的伞衣在=0.04~0.11s间，每隔0.01s的应力分布云图和=0.2s和=0.4s的应力分布云图。由图可见，在伞衣展开到稳定的过程中，伞衣盘上应力最大的区域是逐渐由伞顶孔处向伞衣中部区域移动，而伞带部分相对来说应力较小。因此，在伞衣的结构设计方面，应考虑通过加强带的设计改进或者伞衣材料的改进等措施加强伞衣盘的结构强度，这也为伞衣的设计提供了一定的参考。

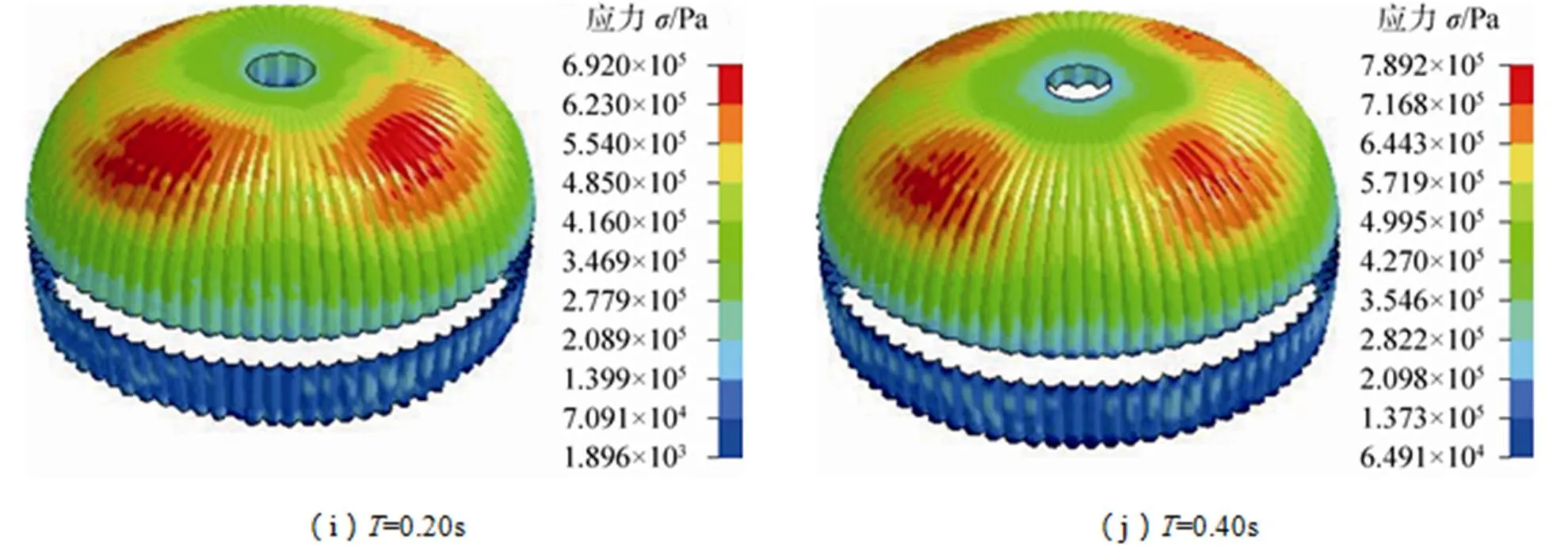
图8 伞衣应力分布云图

为了更直观地观察伞衣表面应力分布，在沿伞衣盘径向每隔0.664m取1个点，如图9所示A，B，C，D，E，F，G，H，I，J，其中A点和J点分别位于顶孔边缘和盘边缘。本文还给出这些点处的有效应力变化过程曲线，如图10所示。由图可知，开伞过程中最大应力值为2.19MPa，出现在I点。从A点到J点，最大应力分布趋势为：应力值从A点到E点持续上升，E点到J点持续下降。I点为整个应力最大值处，这跟伞衣充气的初始外形有一定的关系。伞衣充气稳定后，应力分布符合从A点到E点逐步增大，E点应力最大，E点到J点应力值再逐步减小。伞衣上这10个位置点的应力分布具体数值如表2所示。

图9 研究对象

图10 有效应力曲线图

表2 各点应力最大值及出现时间

Tab.2 Maximum stress and occurrence time of each point

4 结束语

本文对美国某盘缝带伞采用CE/SE方法对其超声速无限质量开伞过程进行了研究。通过将仿真得到的伞衣充满外形和最大开伞动载与空投试验进行对比，验证了数学模型的可靠性，并进一步研究了盘缝带伞的超声速充气过程。通过仿真模拟，得出以下结论：

1）与亚声速开伞类似，超声速开伞在伞衣充满时，投影面积也会经历一个先减小再增大，最后稳定的过程，即降落伞充满时的“呼吸”现象。但从变化值来看，投影面积波动不明显，说明“呼吸”现象不明显，这与盘缝带伞的结构有关，由于其结构透气量大于平面圆形伞，所以充满时的“呼吸”现象没平面圆形伞明显。

2）盘缝带伞超声速开伞充满后，在伞顶孔和伞衣缝处存在一个低压区，这是伞衣结构的原因，使得流过伞顶孔和伞衣缝的气流流速较大。而伞衣口和伞衣内部处于高压区，并且在伞衣口处形成一道弓形激波。

3）在伞衣充气展开到充满稳定的过程中，伞衣盘上应力最大的区域是逐渐由伞顶孔处向伞衣中部区域移动，而伞带部分相对来说应力较小。

4）伞衣充满稳定后，伞衣盘表面的应力分布规律大致为：从伞顶孔到最大伞衣充气外形的最突出处，应力先逐渐增大，在伞衣膨胀最大处应力最高（图9中的E点），从最大膨胀处到伞衣缝，应力再逐渐减小。

[1] 荣伟, 陈旭, 陈国良. 大气密度对降落伞充气性能的影响[J]. 航天返回与遥感, 2006, 27(3): 11-16. RONG Wei, CHEN Xu, CHEN Guoliang. The Effect of Atmospheric Density on Parachute Inflation Performances[J]. Spacecraft Recovery & Remote Sensing, 2006, 27(3): 11-16. (in Chinese)

[2] 荣伟, 陈旭. 火星探测用降落伞研制试验简介[J]. 航天返回与遥感, 2007, 28(1): 12-17. RONG Wei, CHEN Xu. Brief Introduction to the Development of Parachutes for Mars Exploration[J]. Spacecraft Recovery & Remote Sensing, 2007, 28(1): 12-17. (in Chinese)

[3] 于莹潇, 田佳林. 火星探测器降落伞系统综述[J]. 航天返回与遥感, 2007, 28(4): 12-16. YU Yingxiao, TIAN Jialin. Overview of the Parachute System of Mars Probe[J]. Spacecraft Recovery and Remote Sensing, 2007, 28(4): 12-16. (in Chinese)

[4] JUAN R C, KANDIS M, WITKOWSKI A. Opening Loads Analyses for Various Disk-gap-band Parachutes [C]//17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, AIAA 2003-2131, Monterey, California, 2003: 1-17.

[5] CRUZ J R. Wind Tunnel Testing of Various Disk-gap-band Parachutes[C]//17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, AIAA 2003-2129, Monterey, California, 2003: 1-16.

[6] PRASUN N D, SCHOFIELD J T, MICHAEL E L. Flight Reconstruction of the Mars Pathfinder Disk-gap-band Parachute Drag Coefficient [C]//17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, AIAA 2003-2126, Monterey, California, 2003: 1-7.

[7] ALLEN W, ROBIN B. Mars Exploration Rover Parachute Decelerator System Program Overview [C]//17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, AIAA 2003-2100, Monterey, California, 2003: 1-8.

[8] YARO T, ALLEN W. A Summary of Dynamic Testing of the Mars Exploration Rover Parachute Decelerator System [C]//17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, AIAA 2003-2127, Monterey, California, 2003: 1-7.

[9] JUAN R C. Reconstruction of the Mars Science Laboratory Parachute Performance and Comparison to the Descent Simulation[C]//Aerodynamic Decelerator Systems Technology Conferences, AIAA 2013-1250, Daytona Beach, Florida, 2013: 1-20.

[10] DOUGLAS S A, TOMMASO P R, ADAM D S. Mars Science Laboratory Parachute Inversion Phenomenon and Flight Risk Assessment [C]//20th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, AIAA 2009-2956, Seattle, Washington, 2009: 1-12.

[11] ANITA S. Findings from the Supersonic Qualification Program of the Mars Science Laboratory Parachute System[C]//20th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, AIAA 2009-2900, Seattle, Washington, 2009: 1-16.

[12] MICHAEL B. Detached Eddy Simulations of the MSL Parachute at Supersonic Conditions[C]//19th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, AIAA 2007-2529, Williamsburg, 2007: 1-11.

[13] ANITA S. Supersonic Disk-gap-band Parachute Performance in the Wake of a Viking-type Entry Vehicle from Mach 2 to 2.5[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit, AIAA 2008-6217, Honolulu, Hawaii, 2008: 1-9.

[14] VLADIMYR G. Simulation of Fluid-structure Interaction of the Mars Science Laboratory Parachute[C]//26th AIAA Applied Aerodynamics Conference, AIAA 2008-6910, Honolulu, Hawaii, 2008: 1-11.

[15] CHARLES H W, LAMONT R P, THEODORE A T. Post-flight Simulation of Parachute Deployment Dynamics of Viking Qualification Flight Tests[R]. NASA TN D-7415, Hampton, VA: Langley Research Center, 1973.

[16] LINGARD J S, DARLEY M G, UNDERWOOD J C. Simulation of Mars Supersonic Parachute Performance and Dynamics[C]//19th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, AIAA 2007-2507, Williamsburg, VA, 2007: 1-11.

[17] STEPHEN J L, MATTHEW G D. Simulation of Parachute Fluid Structure Interaction in Supersonic Flow[C]//18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, AIAA 2005-1607, 2005: 1-9.

[18] ALLEN W, KANDIS M. Comparison of Subscale Versus Full Scale Wind Tunnel Tests of MSL Disk Gap Band Parachutes [C]//20th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, AIAA 2009-2914, Seattle, Washington, 2009: 1-6.

[19] ALLEN W, KANDIS M, DOUGLAS S A. Mars Science Laboratory Parachute System Performance[C]//Aerodynamic Decelerator Systems Technology Conferences, AIAA 2013-1277, Seattle, Washington, 2013: 1-7.

[20] RICHARD J B, EARLE K H, LUCILLE C C. Performance of a 19.7-meter-diameter Disk-gap-band Parachute in a Simulated Martian Environment[R]. NASA TM X-1499, Hampton, VA: Langley Research Center, 1968.

Study on the Deployment of Disk-gap-band Parachute in Supersonic Flow

YANG Luyu ZHANG Hongying LU Weiwei TONG Mingbo

（Ministerial Key Discipline Laboratory of Advanced Design Technology of Aircraft, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China）

With the development of deep space exploration and landing, it is urgent to study the deployment of parachutes in supersonic flow. In this paper, the Conservation Element and Solution Element Method （CE/SE method） incorporated in the LS-DYNA code is used to simulate a full flexible disk-gap-band parachute which is used in an airdrop test flying in supersonic flow. The full inflation shape of canopy and the maximum of dynamic load of the simulation are in agreement with those obtained in high altitude flight tests of the same parachute, which verifies the reliability of the mathematical model. The process of the inflation is studied in detail, including inflation shape and opening load of the parachute. In addition, the variation of stress and stress distribution of the parachute with time are also presented. The results show that the canopy experiences some “breathing”phenomenon in the process of deployment. At the same time, the mouth of the canopy forms a bow shock. Opening load of the parachute is stable gradually after a large fluctuation; the stress on the disk is higher than that of the band. Therefore, in the design of disk-gap-band parachute, the strength requirements of its disk part should be considered more.

disk-gap-band parachute; inflation; supersonic; CE/SE method; probe landing

（编辑：陈艳霞）

V445.2

A

11009-8518(2016)03-0029-10

10.3969/j.issn.1009-8518.2016.03.004

杨璐瑜，女，1991年生，南京航空航天大学航空宇航学院飞行器设计专业硕士研究生，研究方向为航天器返回技术。E-mail: hyyly_5982@qq.com。

2015-12-03

国家自然科学基金（11002070）；航空科学基金（2012ZC52035）；江苏高校优势学科建设工程基金资助