信息密度与图像主观评价的关系研究

谢佳楠刘兆军李博阮宁娟



信息密度与图像主观评价的关系研究

谢佳楠刘兆军李博阮宁娟

（北京空间机电研究所，北京100094）

在遥感成像系统的研制过程当中，对其性能合理的预估有利于有效地指导系统的设计工作。调制传递函数（MTF）、信噪比（SNR）是较为常用的遥感成像系统的性能预估模型，但它们都无法全面反映遥感成像系统的综合性能。遥感成像系统的信息密度融合了MTF、SNR和边带混叠等多种像质表征参数，能够体现遥感成像系统多方面的性能。文章通过研究信息密度与图像主观评价的关系对信息密度用于预估遥感成像系统综合性能的合理性做了相关的研究。首先，设计不同的遥感成像系统，使其具有不同的信息密度值，以信息密度来体现不同系统的性能优劣；然后，利用不同系统对同一场景进行成像仿真，并对仿真输出的图像进行了主观量化评分；最后，利用相关性分析的手段研究了不同信息密度及其对应的主观评分，研究结果验证了信息密度作为遥感成像系统的一种综合性能预估模型的合理性。

信息密度 主观评价 相关性 航天遥感

0 引言

基于信息理论，空间光学遥感可视为一种信息传递的过程，其中，景物的光强分布是信源，图像形成过程中的退化代表着信息在信道中的丢失，最后获取的图像是信宿。图像采集的过程可以被看作是信源在信道中的有损传输[1]。

遥感成像系统的信息密度是一种对遥感系统信息传递能力的度量，它表征了单位空间面积上成像图像中所保留原始景物的信息量大小。国内外对遥感成像系统的信息密度进行了深入的研究，例如，1975年，美国NASA兰利研究中心的Huck等人在研究一种光机线扫描成像过程时提出了描述这种成像过程的信息密度模型，进而对该成像过程进行了深入的研究[2]；2001年到2003年间，长春光机所的迟学芬等人对于利用信息论评价和优化采样成像系统做了大量的研究[3-5]。

1 遥感成像系统的信息密度

图1为遥感成像系统的通用模型。在轨系统通过采样将连续辐射场转换成数字信号并对其进行压缩后传输到地面处理系统，地面处理系统接收到压缩信号后将其解压缩为数字信号并对其进行图像复原处理得到复原信号[6]，其中，假设压缩信号可以完全由解压缩过程恢复，即假设压缩前信号与压缩后信号一致。

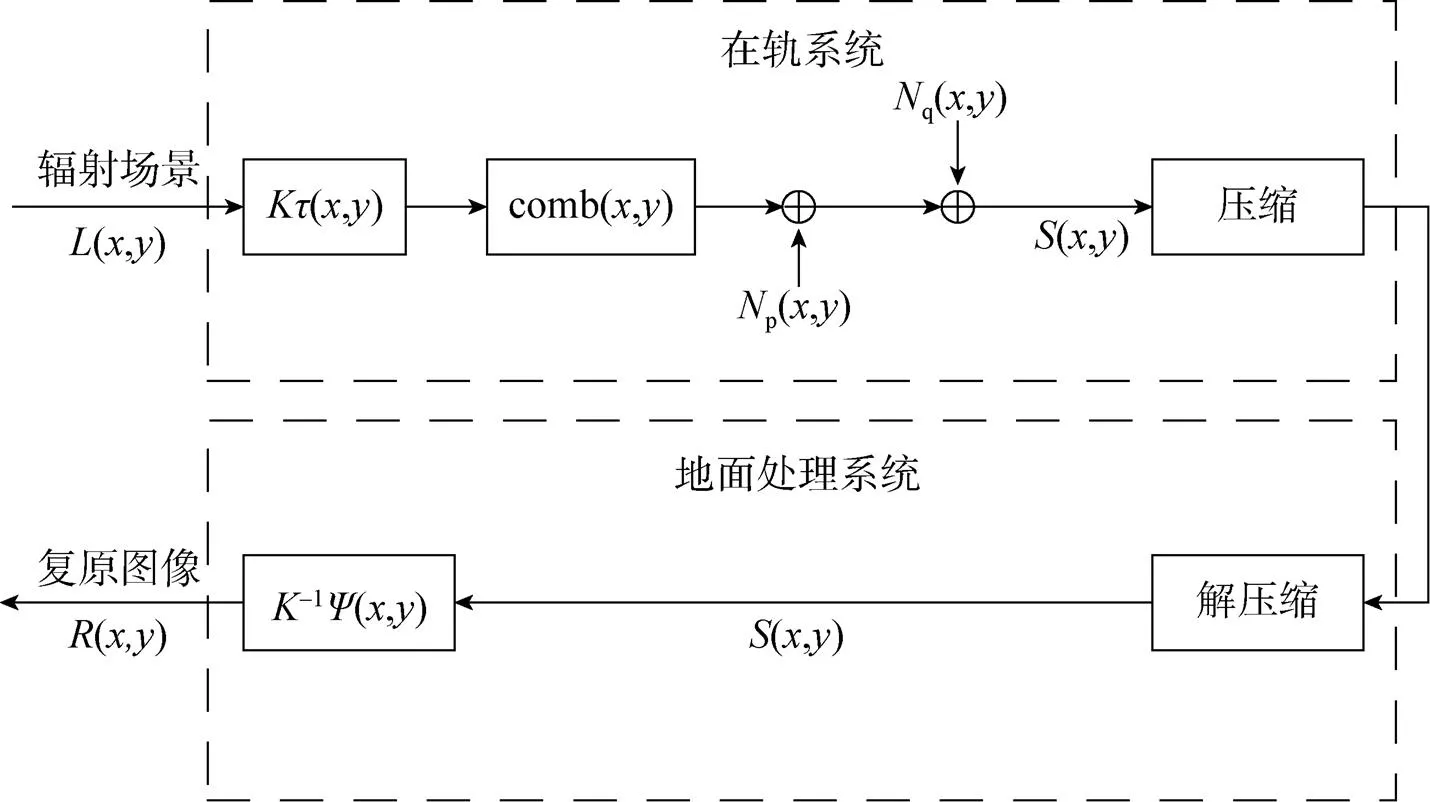
图1 遥感成像系统的通用模型

式中为辐射到传感器信号的稳态转换增益；为图像采集系统的空间响应点扩散函数（其傅里叶变换即系统的MTF）；*为卷积运算符；表示除量化噪声外的几种常见噪声，描述了传感器信号幅度的上下波动；表示量化噪声，数学上可将其转换为具有相同均方根值的随机噪声；表示采样函数，代表在-直角坐标系中以间隔进行采样[7]。

这个成像过程的傅里叶变换为

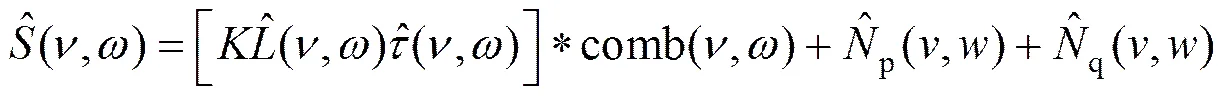
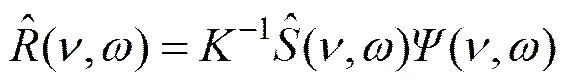
基于信息理论，由以上各式可以得到遥感成像系统的信息密度计算公式[9]

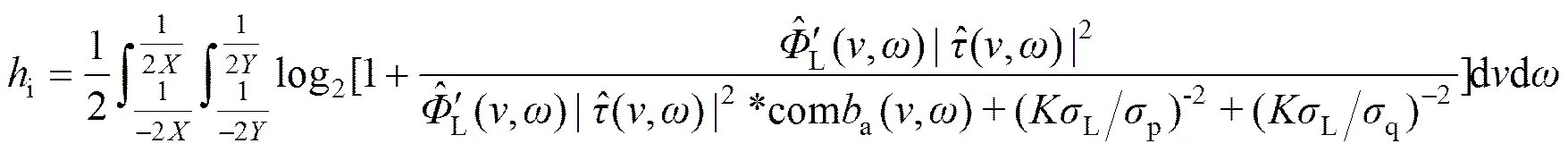
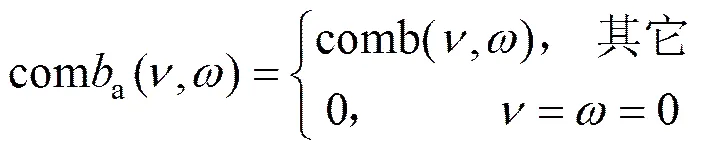
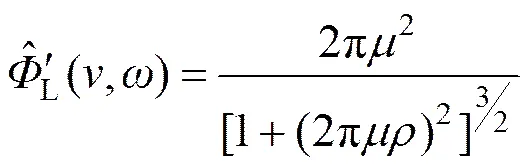
综上所述，遥感成像系统的信息密度函数是融合了MTF、信噪比、边带混叠等多种成像质量（Quality，以下同）表征参数的综合性成像质量表征参量，可以对遥感成像系统的性能作出综合评价。同时由信息密度的函数可以看出，根据系统的参数及其成像条件可以计算信息密度所涵盖的各个参数的值，进而由这些参数计算该系统的信息密度。

2 图像的主观相对质量评价原则

图像质量的评价方法主要分为主观评价方法和客观评价方法两大类[13]。其中，图像质量的主观评价方法是通过人的主观感受对图像质量进行评价。

本文的研究基于人对图像中特定目标的评价，由于人是所有图像的最终感知者与使用者[14]，因此相对于图像的客观评价，本文采用图像的主观评价作为研究对象之一。具体的评价采用了一种主观相对质量评价的方法，该方法是由专业人员对待评价图像做主观上的比较并给出评分。按照是否参考原图，本文采用的这种方法有两种评分原则。

第一种方式是将原图作为所有待评价图像的唯一参考标准，其评分原则为：原图，100分；与原图几乎没有差别，90分以上；与原图相比略有下降，80~89分；与原图相比有明显差别，60~79分；与原图相比失真严重，60分以下。

第二种方式不以原图作为参考图像，只在待评价图像之间进行相对评分，其评分原则为：最优图像，90分以上；中等质量图像，70~89分；最差图像，60~69分。

3 信息密度与图像主观评价关系的相关性试验

3.1 研究方法

图2为信息密度与图像主观评价关系研究的示意图。由信息密度的计算式可知，根据系统的参数及其成像条件可以计算对应的信息密度，因此，第一步根据系统参数的不同获得了个具有不同信息密度的成像系统；第二步，用这个系统对同一场景进行仿真得到仿真图[15]；第三步，由5名专业人员对仿真图进行主观相对质量评价并取评分的均值；最后，比较信息密度和相对质量评分的数据，从而分析信息密度和图像主观质量评价的关系。

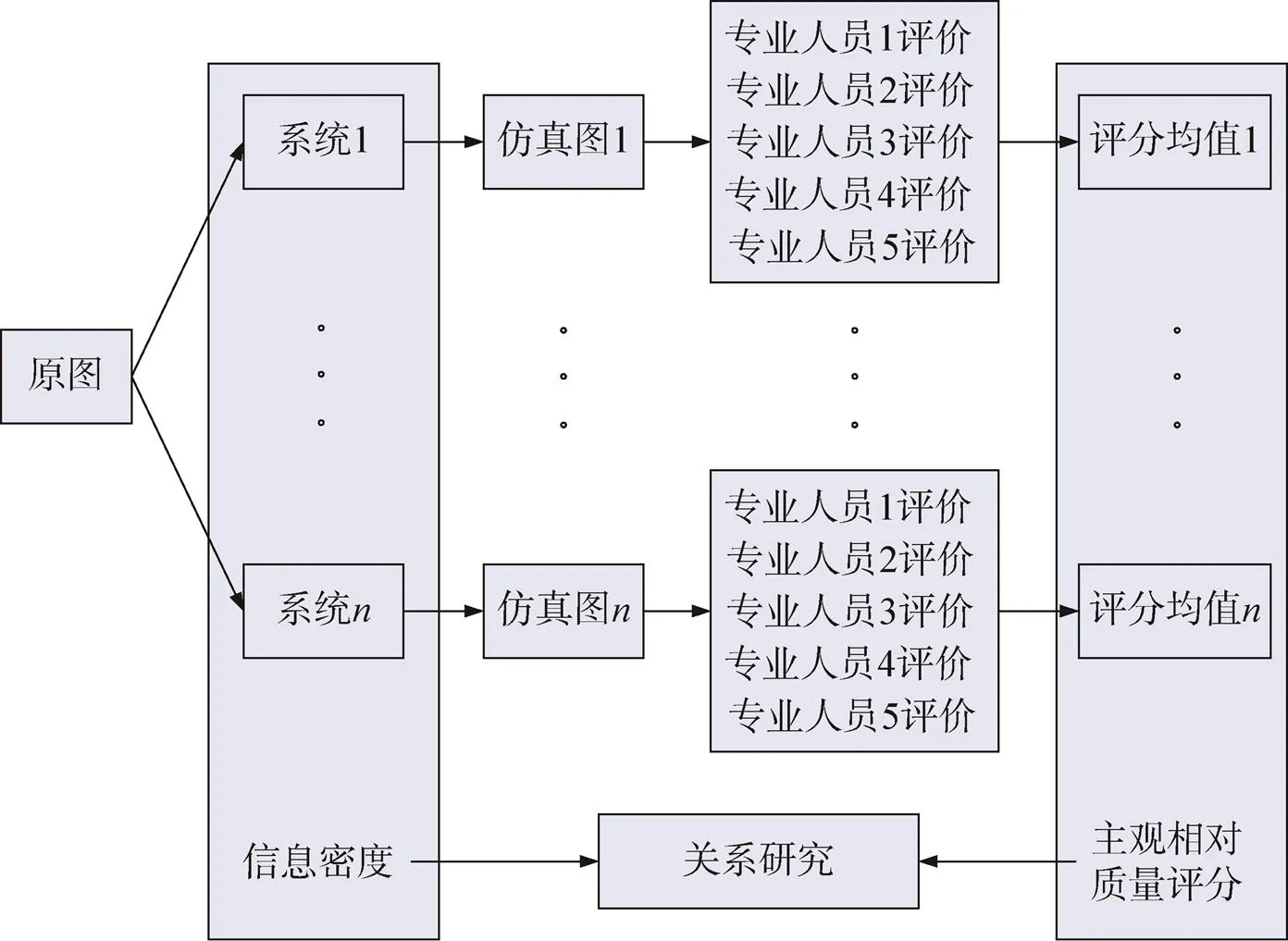
图2 研究方法示意图

图中两个变量关系的研究采用相关性分析，即利用皮尔逊（Pearson）相关系数研究变量之间关系的密切程度，并根据样本推断总体是否相关[16]，其公式为

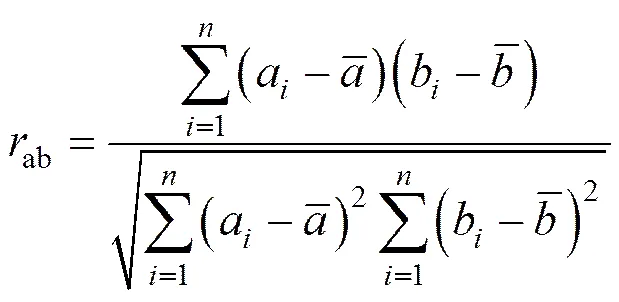
当ab=0，与不存在线性关系，与不相关；当ab>0，随增加而增加，与正相关；当ab<0，随增加而减少，与负相关；当|ab|=l，可以确切地用的线性函数来表示。

由于抽样数据总存在抽样误差，即样本中两变量间相关系数不为0，不能说明总体中两个变量相关，同时，样本中两变量间相关系数为0，也不能保证总体中两个变量间不相关。因此相关性分析必须通过检验。假设：总体中两个变量间的相关系数为0。当该假设成立的概率（显著性）小于5%时，则认为原假设不成立，即两变量是相关的；否则接受原假设，认为总体两变量的相关系数为0。表1给出了临界相关系数表[17]，在算得两个变量相关系数的基础上，该表可用于分析上述检验的显著性水平。基于表1的显著性检验的具体过程如下：假设样本数量为6，算得的相关系数为0.900，对照表1可以看出，在样本数量为6时，当相关系数达到0.811则认为显著性水平为5%，当相关系数达到0.917则认为显著性水平可以达到1%，而算得的相关系数0.900介于0.811和0.917之间，因此可以认为两个变量以95%~99%的置信度（置信度+显著性=1）显著相关。一般情况下，当置信度高于95%，即认为两个变量高度相关。

表1 临界相关系数表

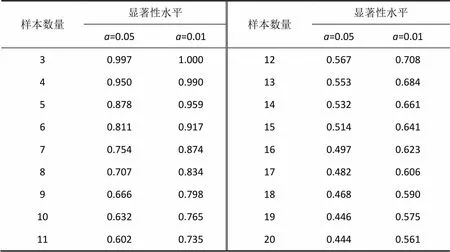
Tab.1 Critical correlation coefficient

3.2 试验结果与分析

基于上述的信息密度与图像主观评价的关系研究方法，试验过程如下：

第一步，设置5个具有不同信息密度值的系统（即本试验的样本数量为5）。本次试验中，不同的系统被人为设置具有不同的的值（为成像谱段的中心波长；为光学系统的F数；为像元尺寸[18]），代表系统的采样频率与光学系统截止频率的比值

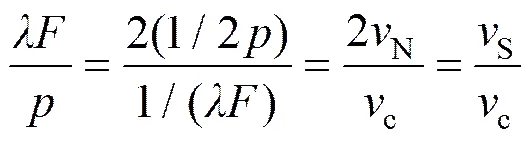
选择作为设置系统差异的关键参数有如下原因：

1）由第1节的结论可知，信息密度可以根据系统的参数计算得到，而包含了和三个系统参数，调整的值可以实现对这三个系统参数的数值的修改，进而获取具有不同信息密度值的系统；

2）为减少系统设置过程的复杂性，系统间存在差异的参数应当尽可能的少，而是采样成像系统优化的重要参数之一，在像元与光学系统的参数匹配方面具有优势；

第二步，选取高分辨率商业卫星图像作为仿真原始场景，利用第一步获取的5个系统对同一场景做仿真，得到5张仿真图。图3所示为其中两个系统仿真图的细节对比，其中图3（a）为系统1（=0.4）的仿真图，图像较模糊，图像质量较差，图3（b）为系统3（=1.0）的仿真图，较之图3（a）更清晰，图像质量更好，通过两张图的细节对比，可以看出不同系统的仿真图存在品质差异。

（a）系统1（=0.4）的仿真图 （b）系统3（=1.0）的仿真图

（a）Emulational image of 1st system（=0.4）（b）Emulational image of 3rd system（=1.0）

图3 仿真图细节对比

Fig.3 Details comparison of emulational image

第三步，由5名专业人员根据主观相对质量评分的第二种评分原则（即不参考原图）对仿真图进行评价并取评分的平均值，系统的信息密度与评价结果如表2所示。

表2 第一次试验结果数据

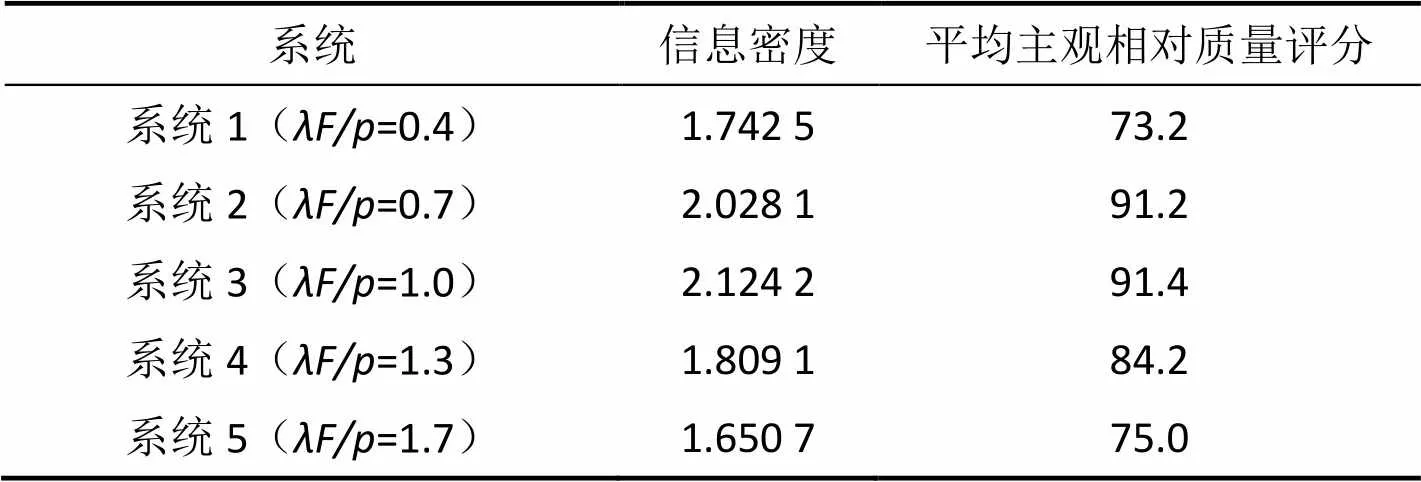
Tab.2 Result data of the first experiment

由以上结果计算的皮尔逊相关系数为0.926，对照表1的临界相关系数表，样本数量为5时95%置信度水平的相关系数为0.878，因此，本次试验的相关系数超过了95%的置信度水平。因此，信息密度与图像质量相对主观评价高度相关。

为增强结论的可信度，在第一次试验的基础上又进行了一次试验。本次试验方法与第一次试验基本相同，为增加与第一次试验数据的独立性，第二次试验与第一次试验有如下区别：

1）系统数量（即试验的样本数量）由第一次的5个调整为15个；

2）系统间存在差异的参量由第一次的调整为和分辨率GSD两个参量；

3）分别对含有靶标的平原场景（以下称为场景1）和港口场景（以下称为场景2）两种场景进行了试验；

4）评分阶段引入原图，采用主观相对质量评分的第一种评分原则。

试验结果的散点图如图4所示。可以看出，无论对于场景1还是场景2，试验数据都显示信息密度与图像质量评分具有近似的线性相关性。具体试验数据见表3。本次试验对场景1计算的相关系数为0.753，对场景2计算的相关系数为0.744，对照根据表1的临界相关系数表，样本数量为15时99%置信度水平的相关系数为0.641，因此，本次试验的两个计算结果都超过了99%的置信度水平。因此，本次试验得到了与第一次试验相同的结论：信息密度与图像质量相对主观评价高度相关。因此，成像系统的信息密度的提升能有效地提高图像质量。

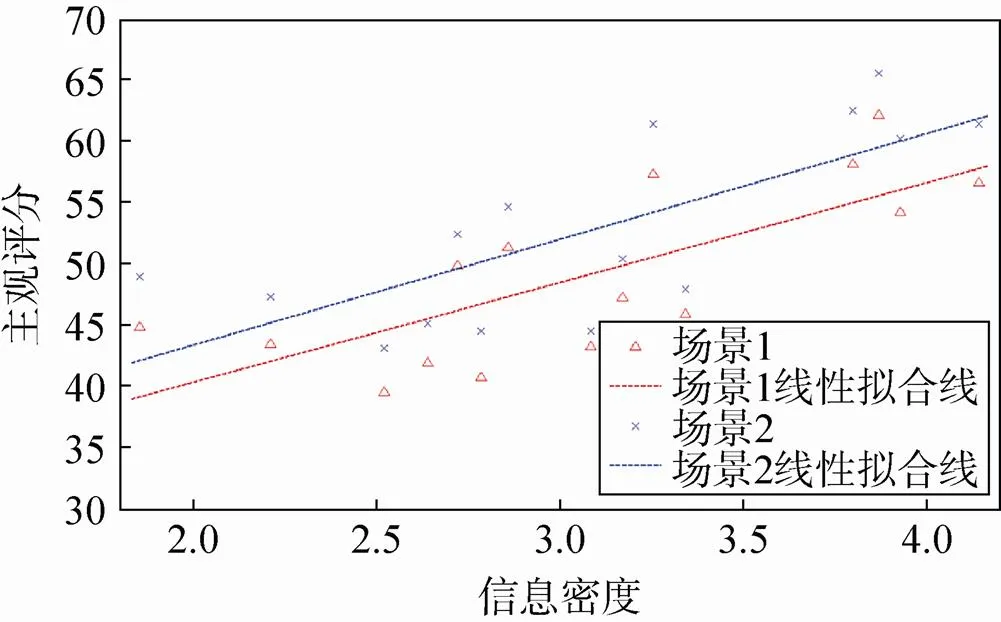
图4 试验数据散点图

表3 第二次试验结果数据

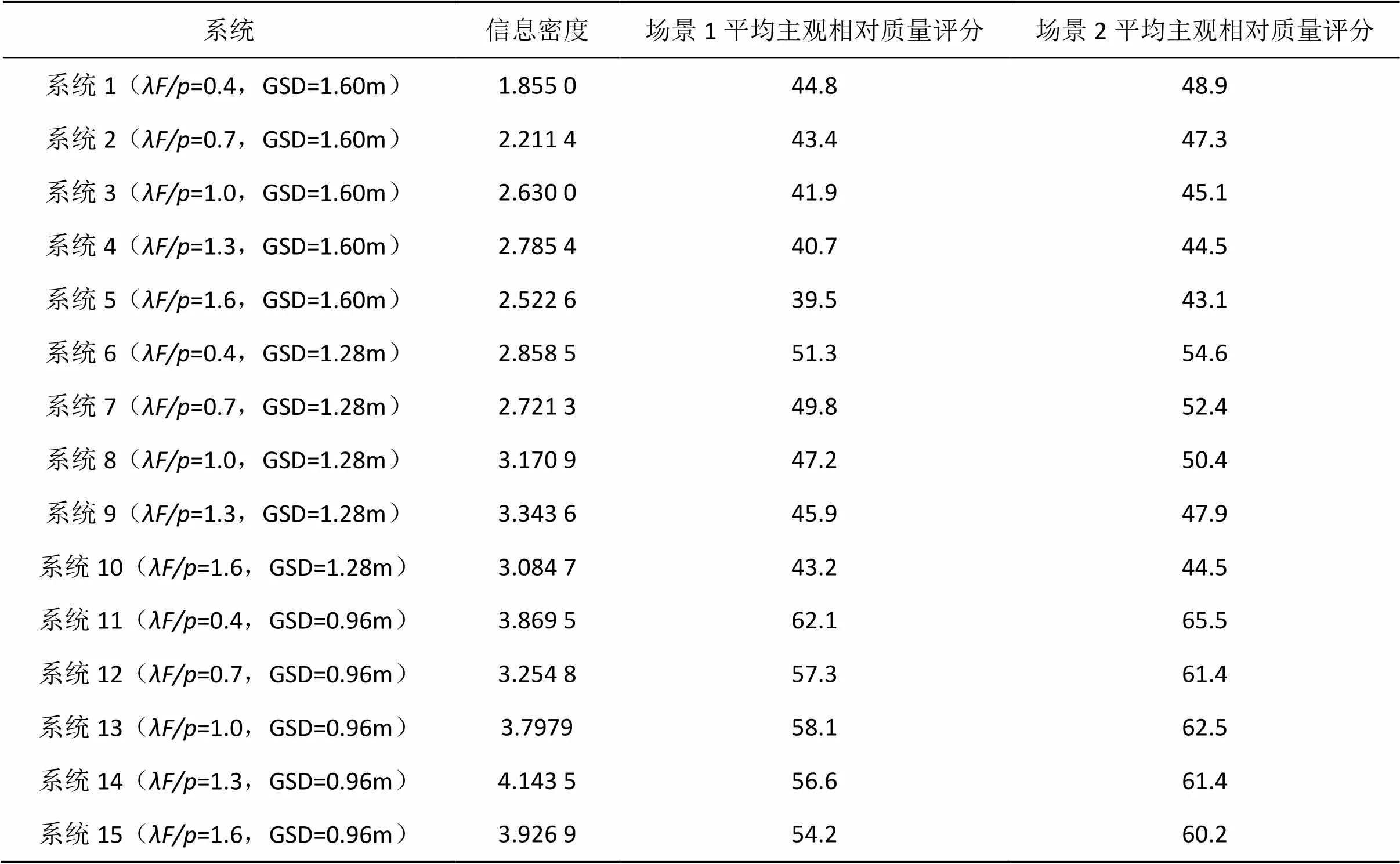
Tab.3 Result data of the second experiment

4 结束语

本文以图像主观相对质量评分作为衡量图像质量的参量，利用相关性分析的方法研究了遥感成像系统的信息密度与图像主观质量之间的关系，分析结果显示信息密度与图像主观质量之间高度相关。因此，信息密度可以作为遥感成像系统的综合性能预估参量，从而有效指导系统设计工作。

[1] COVER T M, THOMAS J A. 信息论基础[M]. 北京: 机械工业出版社, 2007. COVER T M, THOMAS J A. Elements of Information Theory[M]. Beijing: China Machine Press, 2007. (in Chinese)

[2] HUCK F O, PARK S K. Optical-mechanical Line-scan Imaging Process: Its Information Capacity and Efficiency[J]. Applied Optics, 1975, 14(10): 2508-2520

[3] 迟学芬, 于银辉, 易志栋, 等. 互信息量用于采样成像系统的评价[J]. 长春邮电学院学报, 2001, 19(3/4): 24-28. CHI Xuefen, YU Yinhui, YI Zhidong, et al. Assessment of Sampled Imaging System Based on Mutual Information[J]. Journal of Changchun Post and Telecommunication Inistitute, 2001, 19(3/4): 24-28. (in Chinese)

[4] 迟学芬, 韩昌元. 基于信息理论的采样成像系统评价方法[J]. 光学精密工程, 2003, 11(2): 207-211. CHI Xuefen, HAN Changyuan. Assessment of Sampled Imaging System Based on Information-theory[J]. Opics and Precision Engineering, 2003, 11(2): 207-211. (in Chinese)

[5] 迟学芬, 韩昌元, 易志栋. 基于信息理论的采样成像系统匹配设计[J]. 光学学报, 2003, 23(3): 278-283. CHI Xuefen, HAN Changyuan, YI Zhidong. Matching Design Methods Based on Information Theory in Sampled Imaging Systems[J]. Acta Optica Sinica, 2003, 23(3): 278-283. (in Chinese)

[6] BORN M, WOLF E. Principles of Optics[M]. UK: Cambridge University Press, 2001.

[7] 马文坡. 航天光学遥感技术[M]. 北京: 中国科学技术出版社, 2010. MA Wenpo. Space Optical Remote Sensing Technology[M]. Beijing: China Science and Technology Press, 2010. (in Chinese)

[8] 鲁敏. 遥感图像质量评价方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2013. LU Min. Research on Assessment Methodology of Remote Sensing Image Quality[D]. Harbin: Harbin Institute of Technology, 2013. (in Chinese)

[9] 迟学芬. 基于信息理论的采样成像系统评价与系统技术研究[D]. 长春: 长春光学精密机械与物理研究所, 2003. CHI Xuefen. Information-theory Based Assessment and Technical Research of Sampled Imaging System[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, 2003. (in Chinese)

[10] 修吉宏. 基于图像功率谱的航空图像质量判别技术研究[D]. 长春: 长春光学精密机械与物理研究所, 2005. XIU Hongji. Aerial Image Quality Evaluation Based on Image Power Spectra[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, 2005. (in Chinese)

[11] 屈颖歌, 曾生根, 夏德深. 从图像信息容量和图像功率谱看CBERS-1卫星图像[J]. 航天返回与遥感, 2002, 23(2): 40-45. QU Yingge, ZENG Shenggen, XIA Deshen. Appraise the CBERS- 1 Image Quality with Image Information Capacity and Power Spectrum[J]. Spacecraft Recovery & Remote Sensing, 2002, 23(2): 40-45. (in Chinese)

[12] FIETE R D, TANTALO T. Comparison of SNR Image Quality Metrics for Remote Sensing System[J]. Optical Engineering, 2001, 40(4): 574-585.

[13] 任雪. 图像质量客观评价方法的研究与实现[D]. 南京: 南京航空航天大学, 2008. REN Xue. Research and Realization of the Objective Image Quality Assessment Methods[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008. (in Chinese)

[14] 刘书琴, 毋立芳, 宫玉. 图像质量评价综述[J]. 中国科技论文在线, 2011, 6(7): 501-523. LIU Shuqin, WU Lifang, GONG Yu. Overview of Image Quality Assessment[J]. Sciencepaper Online, 2011, 6(7): 501-523. (in Chinese)

[15] 阮宁娟, 庄绪霞, 李妥妥, 等. 空间光学遥感系统全链路仿真与分析[J]. 航天返回与遥感, 2013, 34(6): 36-43. RUAN Ningjuan, ZHUANG Xuxia, LI Tuotuo, et al. End to End Simulation and Analysis of Space Optical Remote Sensing System[J]. Spacecraft Recovery & Remote Sensing, 2013, 34(6): 36-43. (in Chinese)

[16] 孙景峰, 张旭春, 李春杰, 等. 相关性分析在高考质量评价研究中的应用[J]. 齐齐哈尔师范高等专科学校学报, 2011(5): 27-28. SUN Jingfeng, ZHANG Xuchun, LI Chunjie, et al. On the Application of Correlation Analysis in the Research of College Entrance Examination Quality Assessment[J]. Journal of Qiqihar Junior Teachers’ College, 2011(5): 27-28. (in Chinese)

[17] 李云雁, 胡传荣.试验设计与数据处理[M]. 北京: 化学工业出版社, 2012. LI Yunyan, HU Chuanrong, et al. Experiment Design and Data Processing[M]. Beijing: Chemical Industry Press, 2012. (in Chinese)

[18] FIETE R D. Image Quality and λFN/p for Remote Sensing System[J]. Optical Engineering, 1999, 38(7): 1229-1240.

Research on Relationship between Information Density and Subjective Assessment of Image

XIE Jia’nan LIU Zhaojun LI Bo RUAN Ningjuan

（Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）

In the design process of a remote sensing imaging system, it is helpful to reasonably estimate the system performance for effective direction of design of the system. The modulation transfer function(MTF) and the signal noise ratio(SNR) are popularly used to estimate the performance of an imaging system. However they cannot reflect the comprehensive performance of the system. The information density, which is the function of MTF、SNR、sideband aliasing and many other parameters, can be used to represent comprehensive performance of the system. In this paper, the reasonability of estimating the system performance with information density is studied through researching the relationship between the information density and the subjective image quality.Firstly, different systems are designed to have different information densities, the information density is used to evaluate the performance of different remote sensing imaging systems. Secondly, the same scene is simulated by different systems and then the emulational images are subjectively evaluated. Finally, the relationship between the information density and subjective evaluation is studied with the correlation analysis method. It is verified that it is reasonable to use information density as one of estimation models of comprehensive performance of the remote sensing imaging system.

information density; subjective evaluation; correlation; space remote sensing

（编辑：王丽霞）

O438

A

1009-8518(2016)03-0120-08

10.3969/j.issn.1009-8518.2016.03.014

谢佳楠，男，1988年生，2010年获武汉理工大学光信息科学与技术专业学士学位，现在中国空间技术研究院光学工程专业攻读硕士学位。研究方向为空间光学遥感器系统设计。E-mail: aerospace@aliyun.com。

2016-03-31

国家重大科技专项工程