基于相似理论的电力系统动态等值精确度量化评价方法

朱 林，盛启亮，刘 平，付 东，武志刚

(华南理工大学 电力学院，广东 广州 510640)

基于相似理论的电力系统动态等值精确度量化评价方法

朱 林，盛启亮，刘 平，付 东，武志刚

(华南理工大学 电力学院，广东 广州 510640)

提出一种基于相似理论的电力系统动态等值精确度量化评价的方法。首先，利用Prony算法提取原系统和等值系统故障下的动态特征，即不同阶数的振荡模式，基于相似理论寻找原系统和等值系统振荡模式中的相似部分。然后，根据相似振荡模式中的频率、阻尼、幅值等信息定义动态等值频率相似度和阻尼相似度2个指标。该指标能够精确量化原系统与等值系统动态特性方面的近似程度，且其物理概念与发电机机械参数及控制环节参数相关，可作为判据指导其优化调整。南方电网动态等值案例证明了量化评价方法的合理性及其指标在发电机聚合控制器选取中的应用。

电力系统动态等值；Prony算法；相似理论；量化评价

当前中国电力系统各领域发展迅速，随着交直流联合输电及大区联网运行场景的逐渐增多，现有电网规模及其复杂度也随之迅速攀升。在此背景下，传统的针对大规模电力系统直接进行仿真研究的方法由于仿真时间长及可移植性差等原因，已难以满足现有电力系统快速分析的要求。为有效提高仿真效率，一个行之有效的手段便是将整个系统划分为研究系统和外部系统两部分，并进一步采用动态等值的方法对外部系统进行大规模化简[1]。而动态等值的精确程度会对随后进行的相关分析研究工作造成较为直观的影响。

理想情况下，等值前、后系统故障响应相同，故障仿真曲线应完全重合。为尽量接近上述理想等值结果，现有工程实际通常采用定性分析的方法，即先通过观察等值前后系统故障仿真曲线之间的相似程度来判断动态误差的大小，随后基于该观察结果对发电机及其控制系统参数进行相应调整[2-5]。显然，这种依赖于观察人员自身经验进行误差大小判断的方法缺乏足够的说服力。故如何构建一种能够定量评价动态等值精确程度的方法成为一个亟待解决的问题。

目前，量化评价动态等值精确程度的研究相对较少。文献[6]利用Prony分析方法分别从原系统和等值后系统的故障响应曲线中提取主导振荡模式，并基于主导振荡模式中的特征信息定义了频率和阻尼比误差指标。当故障仿真曲线畸变较严重时，主导振荡模式不能包含多阶振荡模式中的大部分信息。另外，部分相关研究集中于等值模型有效性评估方面，文献[7]提出基于功率灵敏度的等值模型可信度量化评估方法，对不同等值模型具有良好的辨别能力，但由于实际电网机组数量众多，计算系统的功率灵敏度矩阵难度较大。文献[8]基于扩展等面积准则(EEAC)，对故障下等值前、后系统的稳定量化指标进行对比，定义了相关可信度指标。文献[9]指出，对2个组成要素或特性上相似的系统可运用相似学理论分析它们之间的相似程度。文献[10-12]介绍了相似理论及其在仿真可信度、电力暂态信号识别研究中的应用，文献[13]将相似理论运用到电力系统动态仿真误差评价中，并根据相似振荡模式中的特征量定义了反映电力系统仿真相似度的若干指标，获得了较好的工程实际效果。

笔者将相似理论运用到动态等值精确度量化评价方法的研究中。首先，讨论Prony最优分析阶数；其次，基于相似理论提出一种量化评价方法，并定义动态等值频率和阻尼相似度2个量化指标；然后，将所提方法与量化指标应用于动态等值中发电机控制环节的优化中；最后，以南方电网某运行方式数据为例进行案例分析，证明该量化评价方法与量化指标的合理性、实用性。

1 相似理论及其在等值精确度中的应用

1.1 相似理论

相似理论可用于分析组成要素或特性上相似的2个系统之间的相似程度。相似元是指系统间具有共同属性和特征，而在数值上存在差异的组成要素构成的单元。

假设系统A由m个元素组成，系统B由n个元素组成，根据某种选取原则，系统A，B之间存在l个相似元素，即l对相似元。第i对相似元间的相似程度为q(ui)，其对系统之间相似程度的影响权重为βi，那么系统A，B之间的相似程度Q即为关于上述各量的函数，可表示为

Q=f(m,l,n,q(ui),βi)。

(1)

其中，i= 1, 2, ... ,n。

1.2 相似理论在动态等值中的应用

笔者将相似理论运用到电力系统动态等值精确度评价中。对于动态等值工作来说，2个分析系统即为等值前后系统分别对应的包含诸多特征信息的多阶振荡模式，可由Prony分析得到，相似系统为原系统与等值系统多阶振荡模式中的相似部分。

假设原系统某一电气量的某种故障响应Prony分析结果包含m阶振荡模式，相应的等值系统包含n阶振荡模式，通过一定的选取原则可以分别从m，n阶振荡模式中得到l个相似振荡模式，其从属关系如图1所示。

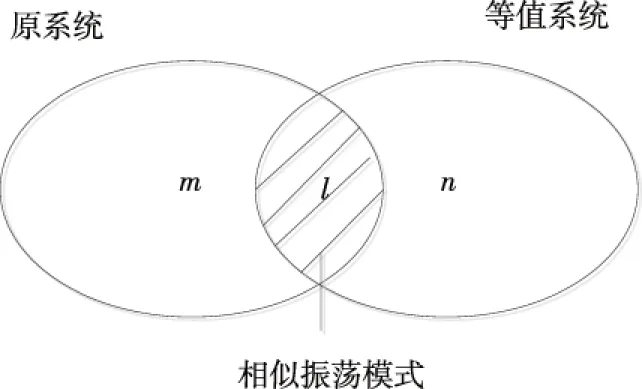
图1 等值前、后系统振荡模式下的韦恩图

l对相似振荡模式之间的近似程度共同决定了原系统与等值系统的相似程度，可用于动态等值精确度的量化评价。

2 Prony算法及最优阶数选取

2.1 Prony算法原理

Prony算法是一种分析等间隔采样信号特征的方法，对等值前、后系统故障响应结果进行Prony分析可以获得给定阶数个包含幅值、频率、阻尼以及相位等特征变量的振荡模式。

假设某条故障响应曲线是一组P个具有任意振幅、相位、频率和阻尼的指数函数的线性组合，其离散时间的函数形式为

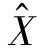
(2)

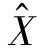
可通过计算得出幅值Ai、相位θi、频率fi和衰减因子αi，即

(3)

2.2 最优阶数选取

利用Prony算法提取电力系统动态特征时，首先要解决分析阶数的问题，阶数选择过低会造成重要数据丢失，一些振荡模式不能被识别导致拟合误差较大，而过高的阶数选择则增加了计算量，同时会引入大量的冗余振荡模式。可利用信噪比(SNR)及拟合百分比误差(EBF)2个指标作为判据选取Prony分析阶数。

SNR是常用的拟合指标，定义为

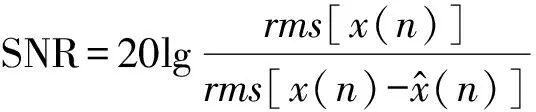
(4)

其中，rms表示均方根，dB。SNR的值越大，表示拟合的精度越高。一般认为，当SNR>40时，拟合精度达到要求。

拟合百分比误差EBF定义为

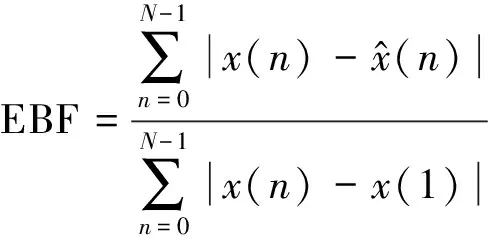
(5)

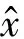
对于采样点总数N，设定所有可能的分析阶数P=1,2,…,N，计算其SNR及EBF结果，其中，SNR最大且EBF最小对应的阶数即为最优阶数，若SNR最大时阶数与EBF最小时阶数不一致，根据经验，选取SNR最大时对应阶数进行Prony分析效果更精确。

3 等值前、后相似振荡模式寻找

3.1 振荡模式筛选

采用Prony算法分析动态等值前后系统的故障响应曲线，可以获得给定阶数P个振荡模式。其中往往包含了大量幅值接近0的冗余部分，故在根据相似原理寻找相似振荡模式前首先需要消除振荡模式中的冗余项。

观察Prony分析的结果发现，各振荡模式能量Ei大小差距明显，且绝大部分能量是由少数模式决定的。第i个振荡模式的能量Ei由该振荡模式下各采样点模值的平方和得到：

Ei=Aiexp(jθi)·exp(n·Δt·(αi+j2πfi)) 。

(6)

其中，n= 1, 2, …,N-1，Ai，fi，αi，θi分别为振荡模式i的幅值、频率、阻尼以及相角。

现规定一个能量阈值v=99.9%，将所有振荡模式按照能量从高到低排序，并依次累加直到所得能量不小于总能量∑Ei与v的乘积：

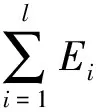
(7)

利用上述方法消除等值前、后振荡模式中的冗余项后，可获得包含绝大多数信息的等值前l阶振荡模式，l远小于Prony分析阶数P，简化了相似振荡模式的寻找过程。

3.2 相似振荡模式获取

按照三者欧氏距离最小原则，以等值前曲线l阶振荡模式为基准，在等值后曲线m阶Prony振荡模式中寻找相似振荡模式。对于i=1,2,…,l，j=1, 2 ,…,m，计算：

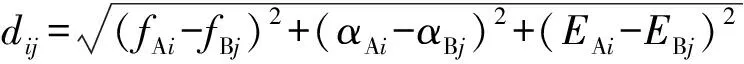
(8)

对振荡模式i，计算获得最小的dij，则等值前曲线振荡模式i与等值后曲线振荡模式j为一对相似振荡模式，在m阶振荡模式中去除振荡模式j，用于下一对相似振荡模式的寻找过程，最终得到l对相似振荡模式。

4 动态等值频率、阻尼相似度指标

4.1 单个故障响应的频率、阻尼相似度计算

前述方法可获取原系统m阶振荡模式以及等值系统n阶振荡模式中的l阶相似振荡模式。第i对相似振荡模式之间的频率相似度：

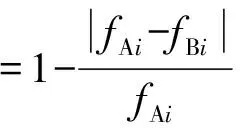
(9)

式中fAi为原系统第i个振荡模式的频率，fBi为等值系统第i个振荡模式的频率。

等值前曲线A的l阶振荡模式中各个分模式的能量与总能量的比值作为该分模式在相似度计算中占全部振荡模式的权重：

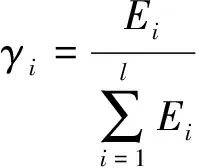
(10)

其中，Ei为原系统第i个振荡模式的能量。

考虑权重后所有相似振荡模式的相似度：

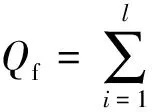
(11)

阻尼相似度计算时要考虑非周期分量的影响，在l阶相似振荡模式基础上添加能量最大的振荡模式，形成阻尼相似度计算所需的l+1阶相似振荡模式。

与频率相似度计算不同，寻找得到的相似振荡模式可能存在阻尼异号的情况，即两振荡模式的稳定趋势完全相反，其对阻尼相似度的贡献为0，第i对相似振荡模式之间的阻尼相似度计算为

(12)

式中αAi为等值前曲线A的Prony分析结果中第i个振荡模式的频率；αBi为等值前曲线B的Prony分析结果中第i个振荡模式的频率。

同样，取等值前曲线A的Prony分析结果中各分振荡模式的能量占所有模式总能量的比例作为阻尼相似度计算时的权重：

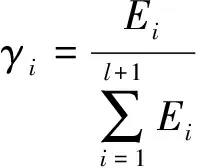
(13)

考虑权重后所有相似振荡模式的相似度：

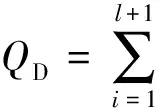
(14)

4.2 动态等值频率、阻尼相似度定义

以上讨论了等值前、后系统中某故障响应曲线，如发电机功角、母线电压和线路功率曲线等的频率相似度和阻尼相似度的计算过程，评价等值工作精确程度需要综合考虑不同故障条件下不同位置、不同类型的响应曲线等值前后的近似程度。

故障设置以能反映系统故障后动态特性为原则，根据工程实际经验，常设置直流故障以及重负荷的500 kV母线三相短路故障等较严重故障，对于每一种故障，待研究仿真曲线主要包括发电机功角曲线、保留母线电压曲线、保留线路有功、无功功率曲线等。

设置仿真故障类型有k种，对每种故障类型i(i=1,2,…,k)，待研究仿真曲线有l对(包括原系统与等值系统)。对于故障类型i，仿真曲线j，经过Prony分析及相似振荡模式提取后，可计算得频率相似度Qf(ij)与阻尼相似度QD(ij)，定义综合考虑不同故障下不同仿真曲线振荡模式的动态等值相似度指标。动态等值频率、阻尼相似度分别为

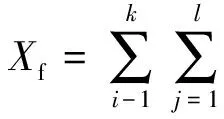
(15)

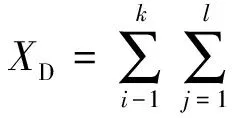
(16)

式(15)、(16)中αi为故障类型i的权重；βj为仿真曲线j的权重。

4.3 指标计算流程

对于k种故障，l对待观察曲线、动态等值频率相似度与阻尼相似度计算流程如图2所示。

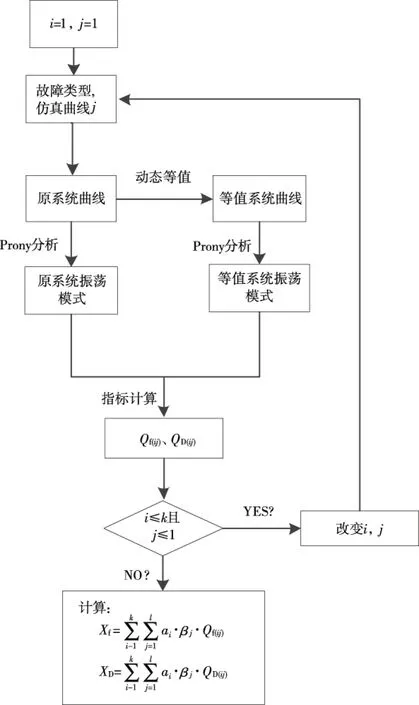
图2 动态等值频率、阻尼相似度指标计算流程

4.4 指标在等值机控制器选取中的应用

大电网动态等值中，等值机控制器的选取一般采用主导模式法，即选取待聚合机群中容量最大的发电机的控制器模型和参数，在此基础上修改部分功率、容量值得到，一般来说该方法效果较好，但对于某些包含不同类型控制器的发电机机群，该等值机控制器选取方法并不合理，因此，需在此基础上进行优化。使用机群内其余发电机的控制器进行替换，通过计算该文提出的各种替换情况下动态等值频率、阻尼相似度，根据计算情况确定合理的等值机控制器是一种简单有效的优化措施。

5 算例分析

选择南方电网某年某运行方式系统作为待等值系统，包含10 000余个节点，1 400余台发电机，

使用南方电网开发的DES动态等值程序对原系统进行等值化简，等值后保留了南方电网的大多数500 kV节点和线路，等值系统包含462个节点，共有49台等值机和119台保留机组。

根据动态等值经验，不设置故障情况下对系统进行暂态仿真，若仿真曲线有振荡则说明存在等值机控制器选择不合理的情况，对于该算例，定位到含不合理控制器的等值机为第11台等值机EQGEN11。

GROUP11包含10台待聚合发电机，分别为MAW1-6以及MSH7-10，根据主导模式法，选取MAW1的控制器作为等值机11的控制器模型，现结合该文所提动态等值频率、阻尼相似度指标对控制器选取进行优化。

使用GROUP11内其余发电机的控制器进行替代，对于该算例，设置故障1，2,3，分别是楚穗直流单极闭锁、北增线北侧三相短路及肇砚线肇侧单瞬故障。对于每一种故障，待研究仿真曲线有安顺、肇庆、北郊换流母线电压；以坪石为参考发电机，有小湾电厂、岩滩发电机功角；重要联络线施秉-黎平、梧州-罗洞、玉林-茂名线路有功功率。根据图2指标计算流程，计算每种控制器选取方式下动态等值频率、阻尼相似度如表1所示；故障1，2，3下等值前、后系统部分仿真曲线如图3～7所示。

表1数据频率、阻尼相似度的大小反映出各种替换情况下的等值精确程度，可以看出，选取MAW5控制器作为等值机11控制器时计算得到的频率、阻尼相似度均为最大，即MAW5为最合理的替换方案。图3～7等值机11控制器选择MAW5和MAW1时等值前、后系统故障响应的仿真结果对比显示选择MAW5更接近于原系统，验证了表1中数据的正确性，证明了该文提出的动态等值频率、阻尼相似度的合理性。

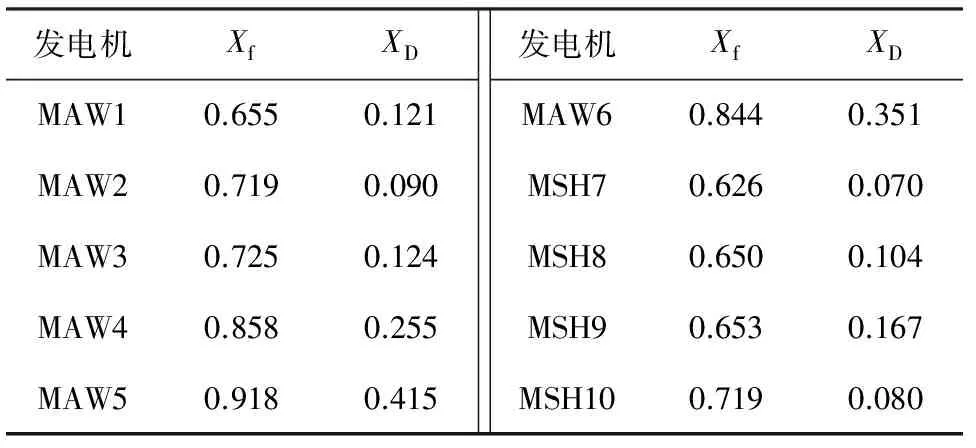
表1 等值机11选取不同控制器模型时频率、阻尼相似度

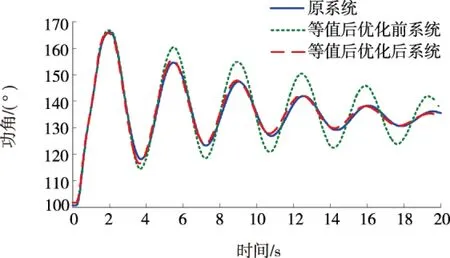
图3 故障1下小湾发电机功角曲线

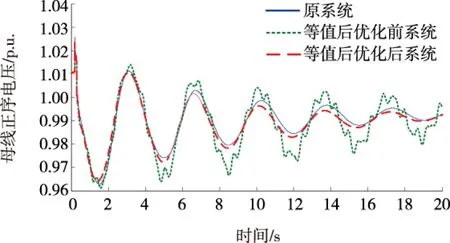
图4 故障1下肇庆换流站电压曲线

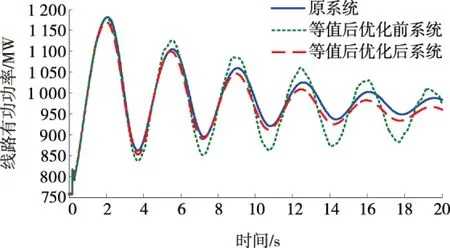
图5 故障1下梧州-罗洞线路有功功率曲线

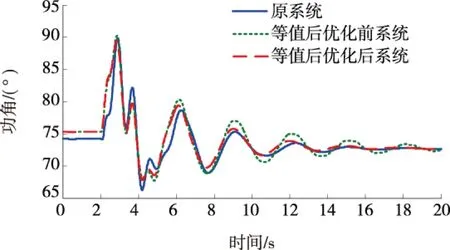
图6 故障2下岩滩发电机功角曲线

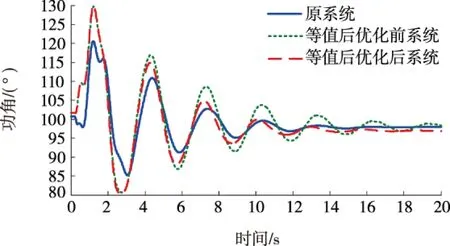
图7 故障3下小湾发电机功角曲线

6 结语

笔者将相似理论引入到动态等值精确度量化评价研究中，并提出一种有效的评价方法，根据等值前后系统不同故障响应的特征提取结果定义了动态等值频率、阻尼相似度指标，并给出了Prony最优分析阶数的选取原则以及相似度指标的详细定义过程。该量化评价方法综合考虑了等值前后系统故障响应的全部特征信息，从振荡模式的角度描述了原系统与等值系统故障仿真结果的相似程度。系统的振荡模式特征信息与电力系统的诸多变量尤其是发电机参数有直接关联，故该指标可以作为判据指导动态等值中参数的进一步优化与改进。

[1]倪以信，陈寿孙，张宝霖．动态电力系统的理论和分析[M]．北京：清华大学出版社，2002.

[2]胡杰，余贻鑫．电力系统动态等值参数聚合的实用方法[J]．电网技术，2006，30(24)：26-30． HU Jie，YU Yi-xin．A practical method of parameter aggregation for power system dynamic equivalence[J]．Power System Technology，2006，30(24)：26-30.

[3]JU P，NI L Q，WU F．Dynamic equivalents of power systems with online measurements Part 1: Theory[J]．IEE Transations on Proceedings Generator，2004，151(2) : 175-178.

[4]彭伟，徐泰山．电力系统动态等值中发电机的选择方法[J]．电力系统自动化，2010，34(14)：48-51． PENG Wei，XU Tai-shan．A generator selection method for power system dynamic equivalents[J]．Automation of Electric Power System，2010，34(14)：48-51.

[5]岳程燕.大规模电力系统动态等值中聚合问题的研究[D]．北京，中国电力科学研究院，2001.

[6]张一荻，管霖．交直流互联电网动态等值的实用化方法[J]．电力自动化设备，2013，33(2)：120-125． ZHANG Yi-di，GUAN Lin．Practical dynamic equivalence of AC-DC interconnected power network[J].Electric Power Automation Equipment，2013，33(2)：120-125.

[7]周海强，周晓成，鞠平，等．基于功率灵敏度的动态等值模型可信度量化评估方法[J]．电力系统自动化，2012，36(8)：6-10． ZHOU Hai-qiang，ZHOU Xiao-cheng，JU ping，et al．A quantitative credibility evaluation method of dynamic equivalent model based on power sensitivity[J]．Automation of Electric Power System，2012，36(8)：6-10.

[8]孔祥波，李威，周海强．基于EEAC的动态等值模型可信度评估方法[J]．电力建设，2014，35(5)：1-5． KONG Xiang-bo，LI Wei，ZHOU Hai-qiang．An EEAC-based credibility evaluation method of dynamic equivalent model[J]．Electric Power Construction，2014，35(5)：1-5.

[9]郭薇，李云芝，姜振东．用相似理论讨论仿真的可信度[J]．系统仿真学报，1999，10(2)：113-115． GUO Wei，LI Yun-zhi，JIANG Zhen-dong．Feasibility of simulation obtained by use of similarity theory[J]．Journal of System Simulation，1999，10(2)：113-115.

[10]贾旭东，李庚银，赵成勇，等．电力系统仿真可信度评估方法的研究[J]．中国电机工程学报，2010，30(19)：51-57． JIA Xu-dong，LI Geng-yin，ZHAO Cheng-yong，et al．Study of the credibility evaluation method for the power system simulation[J]．Proceedings of the CSEE，2010，30(19)：51-57.

[11]贺仁睦．电力系统动态仿真准确度的探究[J]．电网技术，2000，24(12)：1-4． HE Ren-mu．Research into veracity of power system dynamic simulation[J]．Power System Technology，2000，24(12)：1-4.

[12]何正友，罗国敏，杨建维．基于小波能谱矩阵相似度的电力暂态信号识别[J]．电力科学与技术学报，2007，22(3)：12-17． HE Zheng-you，LUO Guo-min，YANG Jian-wei．Power transients recognition based on wavelet energy matrixes similarity[J]．Journal of Electric Power Science and Technology，2007，22(3)：12-17.

[13]高松，贺仁睦，马进，等．电力系统动态仿真误差评定准则研究[J]．电力系统自动化，2006，30(4)：6-10． GAO Song，HE Ren-mu，MA Jin，et al．Error criteria on power system dynamic simulation validation[J]．Automation of Electric Power System，2006，30(4)：6-10．

Quantitative evaluation method for power system dynamic equivalent accuracy with similarity theory

ZHU Lin, SHENG Qi-liang, LIU Ping, FU Dong, WU Zhi-gang

(School of Electric Power, South China University of Technology,Guangzhou 510640, China)

A quantitative evaluation method for power system dynamic equivalent accuracy with similarity theory was proposed in this paper. Dynamic characteristics of original and equivalent system, namely oscillation modes with different order, were extracted by Prony algorithm. Similarity theory was used to find similar part of oscillation modes between original and equivalent system, and then two indexes, frequency similarity and damping similarity were defined by the data of frequency, damping and amplitude information. The two indexes reflected the similarity degree of dynamic characteristics between the original and equivalent systems, and can be used as criterion to optimize parameters of equivalent generator because the two indexes are related to parameters of mechanical and controlling unit of generators. Dynamic equivalence example of South China power grid proved the accuracy and reliability of the quantitative evaluation method and the indexes application to the optimization of generator control system.

power system dynamic equivalence; Prony algorithm; similarity theory; quantitative evaluation

2016-06-16

国家自然科学基金(51407079)

盛启亮(1993-)，男，硕士研究生，主要从事电力系统稳定与控制、直流输电等研究；E-mail：mcfcsql@163.com

TM711，TM743

A

1673-9140(2016)04-0116-07