基于北斗的机载终端完好性算法仿真研究
2016-02-13刘瑞华邓明智蔚保国邢兆栋
刘瑞华,邓明智,蔚保国,邢兆栋
1.中国民航大学电子信息与自动化学院,天津300300 2.中国电子科技集团第54研究所,石家庄050081
基于北斗的机载终端完好性算法仿真研究
刘瑞华1,*,邓明智1,蔚保国2,邢兆栋2
1.中国民航大学电子信息与自动化学院,天津300300 2.中国电子科技集团第54研究所,石家庄050081
国内外关于接收机自主完好性算法的理论研究已经成熟,但缺乏依据北斗实测数据的算法性能分析。根据北斗Ⅱ代卫星导航系统14颗星的星座状态及其公开的服务性能,结合民航非精密进近的应用需求,对机载端嵌入自主完好性算法进行仿真研究。首先通过理论仿真,分析了亚太区之内算法的可用性。其次,利用Nov Atel接收机实测的北斗数据,设定不同的场景和故障类型,对算法故障检测和识别的性能进行了研究分析。通过仿真,北斗系统在亚太区之内的平均可见星个数大于7颗,平均水平保护限值小于500 m,能够满足算法的要求。另通过实测研究,算法可以有效地检测并识别出异常的伪距误差(即故障卫星)。结果表明:接收机自主完好性算法适用于当前北斗Ⅱ代卫星导航系统,能够为民用航空非精密进近提供具备完好性保证的服务。
北斗卫星导航系统;完好性;北斗实测数据;非精密进近;算法;仿真
完好性定义为导航系统提供导航信息的置信水平,以及当由于故障(包括卫星故障、星历、电离层风暴和多路径等原因造成的错误[1])而不能提供导航信息时,系统能够在给定时间(即及时告警时间)内向用户告警的能力。并且从用户安全的角度来看,当卫星导航系统用于航空等生命相关的场合时,完好性成为决定性指标。
作为一种非常重要的完好性增强技术——接收机自主完好性(Receiver Autonomous Integrity Monitoring,RAIM)技术包括两个功能[2]:故障检测,即检测卫星是否存在故障;故障识别,即辨识存在故障的卫星,并在导航解算过程中将其排除。在卫星导航系统不能用于导航时,RAIM具有为用户提供及时、有效告警信息的能力,并进行定位解算,计算保护限值,其目的是限定、评估定位结果的可靠程度。
根据 《北斗卫星导航系统公开服务性能规范(1.0版)》[3],北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)系统播发的B1I频点信号覆盖亚太地区(主要指南纬55°~北纬55°、东经70°~东经150°)并提供公开服务。但BDS系统是否能够在机载接收机端满足国际民航组织(International Civil Aviation Organization,ICAO)规定的4个所需导航性能[4](Required Navigation Performance,RNP),即精度、完好性、可用性和连续性,特别是关乎生命安全的完好性需求,尚且欠缺强有力的实测研究。文献[5]虽对北斗区域导航系统的星座状态及其性能进行了仿真研究。但未对BDS系统下用户端完好性及其性能进行研究。联邦航空局(Federal Aviation Administration,FAA)机载辅助导航设备技术标准规范[6](TSO-C129)规定:“航路阶段所有的GPS接收机必须嵌入RAIM算法”。同样未能考证BDS系统下RAIM的可用性。为了研究当前BDS系统能否满足民航需求,本文根据 《北斗卫星导航系统空间信号接口控制文件(2.0版)》[7]对星座参数的概述,提取出6条开普勒轨道根数,利用MATLAB软件仿真形成BDS空间子系统作为源数据端,采用统计平均方法对亚太区RAIM可用性进行分析。另外,利用北斗实测数据设定不同的故障场景和故障类型,基于奇偶矢量法RAIM算法对BDS系统下算法故障检测与识别(Fault Detection and Identification,FDI)的性能进行研究分析。
1 RAIM算法分析
1.1 完好性
本节主要对RAIM监测的完整执行过程进行理论分析。2014年11月,BDS系统正式进入国际海事组织全球无线电导航系统,取得了面向海事应用的国际合法地位[8]。而对于BDS系统在民用航空上的应用,较之海事应用有着更高的性能要求。并且FAA规定越洋、航路阶段机载导航设备必须具备完好性监测功能[6]。为了推进BDS系统的民航应用,本文对BDS系统下RAIM在非精密进近阶段(Non-Precision Approach,NPA)的可用性及其性能进行了研究分析。
RAIM算法的输入量[9]包括观测噪声的标准差,测量几何布局以及所能允许的最大虚警概率和漏警概率。算法的输出是水平保护限值(Horizontal Protection Level,HPL),HPL规定了对于指定的虚警和漏警概率来说能检测出的最小水平径向位置误差。
1.2 观测方程
假设视线范围内存在n颗可见星,则线性化测码伪距观测方程为y=Hx+ε(1)式中:y为带噪声的观测伪距与基于在标称位置和时钟偏差(即线性化点)预测的伪距之间的差值;H为x和y之间的观测矩阵,共有4列,前3列由卫星位置与用户估计位置之间的方向余弦组成,第4列为常值1;x为用户状态列矢量,其元素是相对于标称状态的增量偏离,线性化是围绕这个标称状态进行的,前3个元素是飞机位置的东、北和天分量,而第4个元素是机载接收机时钟偏差;ε为n×1测量误差列矢量,它同时包含随机和确定项(偏差)。假定随机项服从均值为零的高斯分布,其方差为σ2(即用户等效距离误差的方差)。
定义奇偶方程为

式中:p为奇偶向量;Qp为奇偶空间矩阵,且Qp∈R(n-4)×n,并且满足QpH=0,QpQTp=E。Qp矩阵可以由观测矩阵H的QR分解方法得到。
对观测矩阵H做QR分解,即存在H= QR,其中Q为n×n阶正交矩阵,R为n×4阶上三角矩阵。Qp即为QT的后n-4个行向量组成。由式(1)即可得出p向量的数值式,即
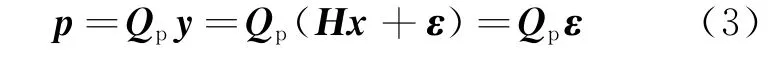
所以,由公式(3)可知,p仅与测量噪声有关,它能直接反应故障卫星的偏差信息,所以基于p矢量可构造检验统计量T,即T=pTp。
检测准则[10]为:当T>Td(Td为检测门限)时,则存在故障卫星;否则,不存在故障卫星。
1.3 RAIM可用性
RAIM可用性是通过比较HPL与特定飞行阶段的水平告警限值(Horizontal Alarm Level,HAL)来确定。可用性准则为:HPL< HAL,则RAIM算法可用;否则RAIM算法不可用。其中,NPA阶段HAL恒为556 m[4], HPL计算式为

1.4 检测门限
假设无偏差存在(即卫星无故障)时,ε服从零均值、标准差为σ的高斯分布。根据统计理论,T服从中心化χ2分布,其自由度为n-4;如若存在故障卫星,则T服从非中心化χ2分布。那么,给定虚警概率PFA(仿真设定为1/ 15 000[9]),检测门限Td计算如下:
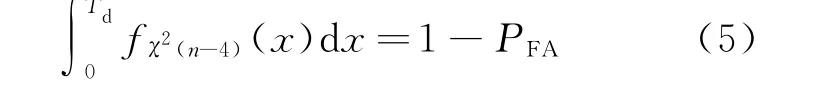
式中:fχ2(n-4)(x)为自由度为n-4的中心化χ2
分布的概率密度函数。
1.5 故障识别
当检测出存在故障卫星时,为保证导航系统继续为用户提供服务,需进行故障卫星的识别与排除,从而限定导航误差符合所允许的容差限值。
故障识别准则[10]:当某颗卫星的特征偏差线最靠近观测的奇偶矢量时,则视该卫星为故障卫星。根据此识别准则:
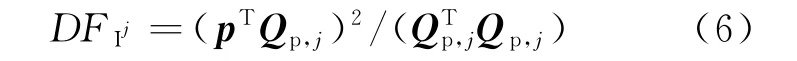
式中:DFIj表示第j颗卫星的识别函数值;Qp,j表示奇偶空间矩阵的第j列元素。由式(6)即可判断出存在故障的卫星。
2 RAIM可用性
2.1 亚太区RAIM可用性
仿真所用BDS星座运行参数取自文献[7],同时借鉴GPS标准定位服务相关的RAIM解决方案[11],仿真出BDS系统下用户观测量,从而对亚太区RAIM可用性进行仿真分析。根据文献[12],在执行RAIM算法之前,必须对RAIM的可用性进行判定。图1、图2和图3分别给出了亚太区2×2格网点上24 h内平均可见星数目分布、平均位置精度因子[9](Position Dilution of Precision,PDOP)分布以及平均HPL分布。
从图1可以看出,亚太区平均可见星数目均大于7,BDS系统在整个亚太区不但能够满足正常定位解算所需的至少4颗可见星数目,而且满足RAIM算法FD和FI功能所分别要求的至少5颗与6颗卫星。从图2可以看出,亚太区平均PDOP值的范围在2.7~3.4之间,反映出亚太区星站几何构型为优良之间[13]。另外,从图3可得:亚太区绝大部分地区上平均HPL值均小于250 m,能够满足RAIM算法的可用性要求,即HPL<HAL。
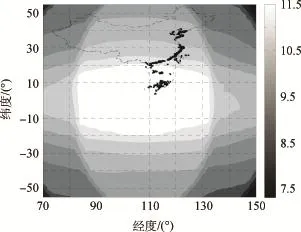
图1 亚太区平均可见星数目分布Fig.1 Satellite visibility for BDS in asia-pacific
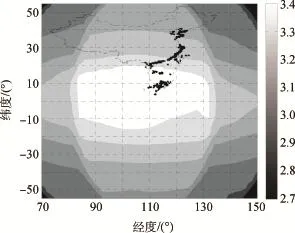
图2 亚太区平均PDOP分布Fig.2 Mean PDOP distribution in asia-pacific

图3 亚太区平均HPL分布Fig.3 Mean HPL distribution in asia-pacific
2.2 静态单点RAIM可用性
仿真设定用户为单点静止状态,用户经纬高为[117.3590° 39.129 5° 6 m],观测区间为[0 s,86 300 s],观测步长为100 s,截止高度角为5°,BDS用户等效测距误差标准差σ=8 m,以NPA阶段RNP为应用对象,运行程序得出观测点24 h可见星星空图、可见星持续时长图、RAIM可用性比较图分别如图4~图6所示。
从图4和图5可以看出,在该用户点24 h观测区间内:1)有些卫星始终存在,例如,编号为161、162、163、164、165的5颗GEO卫星始终存在;2)不同时段内虽然可见星个数相同,但可视卫星组内发生了卫星的切换/更替,星站几何布局发生变化;3)有些卫星在某一时刻切入或者离开视距范围,即在此观测区间内某颗卫星仅存在一段时间;4)可见卫星个数始终大于等于6颗,满足执行RAIM算法和FDI算法对可见星个数的要求。

图4 24 h可见星星空图Fig.4 Azimuth and elevation in 24 hours
由图6可以看出,24 h观测区间内HPL值始终小于HAL,该用户观测点24 h观测区间内星站几何布局始终能够满足RAIM可用性要求,即降低了由于较差的PDOP值而产生误警的概率。

图5 可见星持续时长Fig.5 Visible period of visible satellite

图6 各历元HPL和HAL比较Fig.6 Comparison between HPL and HAL
3 BDS RAIM FDI实测研究
根据第2节关于亚太区的理论仿真结果,本节结合Nov Atel接收机实测的北斗数据,设定了2种故障场景及2种故障类型分别对BDS下RAIM的完整算法流程[14]进行仿真研究。观测地点(38.046 2°,114.435 3°,15.75 m),观测时长2 h,采样间隔5s,截止高度角5°,σ=3 m,误警率为1/15 000,漏警率[9]为10-3。仿真结果分别给出了特定故障场景下伪距故障类型,以及故障排除前后的定位结果(包含经纬度时序关系和水平面定位点分布)。
3.1 仿真场景一
场景一假定观测区间内始终存在某一编号的可视卫星(实测数据中选取162号卫星注入伪距偏差),开始时该卫星伪距值正常,在观测区间内的某一时刻该卫星的伪距值出现异常。针对场景一,给162号卫星分别注入“脉冲式”故障 (即伪距偏差存在于一段观测区间内,且偏差值恒定为50 m,偏差存在的时序区间为[200 1200]);以及“缓变式”故障(伪距偏差存在于一段观测区间内,且偏差值在此区间内与时序成线性关系,最大偏差值为50 m)。两类故障伪距的误差时序图分别如图7和图8所示。
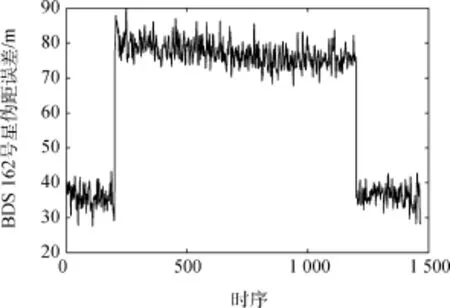
图7 “脉冲式”伪距误差时序关系Fig.7 Relationship between the pseudo-range error and time
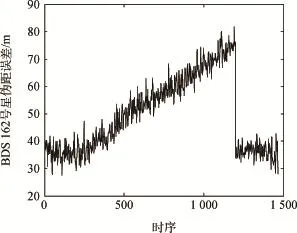
图8 “缓变式”伪距误差时序关系Fig.8 Relationship between the pseudo-range error and time
(1)“脉冲式”故障类型
针对“脉冲式”故障,图9~图11为经过RAIM算法处理前后所得仿真结果。
由图9可知,故障存在时,用户经纬度值(实线表示)出现了明显的偏离现象;故障排除之后,用户经纬度值(虚线表示)恢复正常,几乎无波动。RAIM算法有效地排除了“脉冲式”故障。
由图10可知:故障排除前,解算的用户坐标出现了分离;经纬度最值之间相差了0.0001°;由图11可知:故障排除后,在同等精度下,用户经纬度值几乎保持不变。图10和图11对比可知:经过RAIM算法正确检测并排除故障之后,一方面可以保证用户的定位精度;另一方面,也反映了奇偶矢量RAIM算法具备较高的检测率和识别率。
(2)“缓变式”故障类型
对比“脉冲式”故障伪距误差。“缓变式”故障伪距误差呈现逐渐加大的形式,而非突变。针对此类故障情形,同样采用第2节所述的RAIM算法进行故障检测与识别,仿真结果分别如图12~图14所示。

图9 故障排除前后用户纬度/经度对比Fig.9 Latitude/longitude comparison
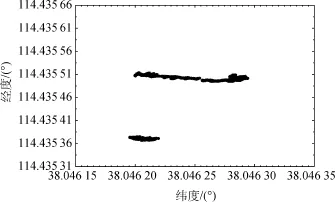
图10 故障排除前定位点水平面分布Fig.10 Horizontal distribution with faulty satellite
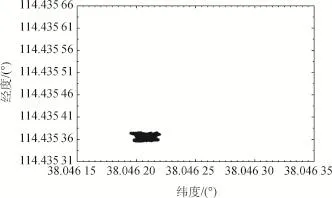
图11 故障排除后定位点水平面分布Fig.11 Horizontal distribution without faulty satellite

图12 故障排除前后用户经度/纬度对比Fig.12 Latitude/longitude comparison
由图12可知:故障排除之前,经纬度值均以线性递增的形式出现不同程度的偏离现象;针对“缓变式”故障,仅当伪距误差大于最小可检测偏差[15]之后,才能有效排除故障,即用户经纬度值在故障开始的一段时间之后才能恢复正常。
由图13可知:故障排除前,解算的用户位置呈现连续不断缓慢偏移的现象;经纬度最值之间也相差了0.000 1°;由图14可知,故障排除后,在同等精度下,用户经纬度值始终保持不变。由图13和图14对比可知:如若故障伪距误差呈现缓慢变化的趋势,该RAIM算法同样可以有效检出故障并予以识别。
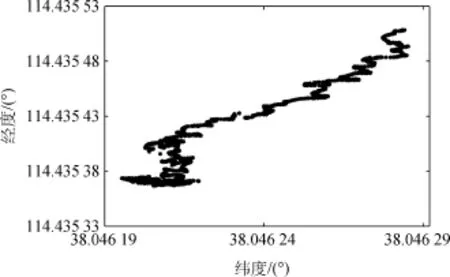
图13 故障排除前定位点水平面分布Fig.13 Horizontal distribution with faulty satellite

图14 故障排除后定位点水平面分布Fig.14 Horizontal distribution without faulty satellite
3.2 仿真场景二
场景二假定故障卫星始终存在,但未必出现在观测区间内。即在观测区间内故障伪距随故障卫星的出现而出现,随故障卫星的离开而离开。
实测数据中设定编号为172号的北斗卫星存在故障,且伪距偏差值恒为50 m,其他仿真条件和参数设置和场景一相同。观测区间内故障卫星的伪距误差(已注入偏差)如图15所示。其中,伪距误差值为0,说明故障卫星未出现在可视范围之内。
针对场景二,经过RAIM处理前后所得仿真结果如图16~图18所示。仿真结果表明:当存在故障且未被排除前,解算的用户位置分布较为分散,经纬度值(实线所示)明显出现偏离现象。但在正确排除故障卫星之后,解算的用户位置较为集中,并且经纬度值恢复至合理波动区间,同时也体现出BDS较好的几何布局(图2中PDOP值均小于4)以及RAIM算法较高的识别率。

图15 伪距误差时序关系Fig.15 Relationship between the pseudo-range error and time

图16 故障排除前后用户经度/纬度对比Fig.16 Latitude/longitude comparison
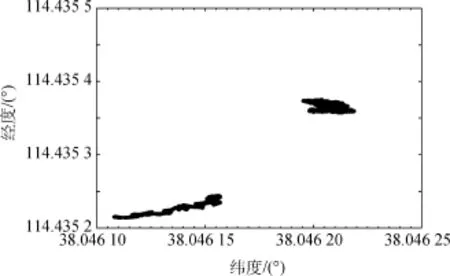
图17 故障排除前定位点水平面分布Fig.17 Horizontal distribution with faulty satellite

图18 故障排除后定位点水平面分布Fig.18 Horizontal distribution without faulty satellite
4 结束语
本文根据北斗导航系统管理办公室已公布的北斗区域卫星导航系统的星座状态以及其服务性能,通过理论仿真和实测研究,可以得出:在亚太区域内,BDS系统下HPL值和可见星数目均满足RAIM算法的需求,可以在机载端实现完好性监测功能,能够为民航提供较优的导航服务。
文中对于静态用户实测的北斗数据设定了2种仿真场景和2种故障类型,分析了当前BDS下RAIM算法的性能,归类研究结果如下:
1)对于“脉冲式”故障类型,奇偶矢量RAIM算法可以完全有效检出并排除故障伪距,表明针对此类故障,RAIM算法能够满足NPA阶段所需完好性要求。
2)至于“缓变式”故障类型,RAIM算法存在一定的适用条件,即故障伪距误差大于最小可检测偏差。
对于未来完全运行状态下的BDS系统,其更密集的星座分布,更完善的完好性保证体系建设,以及更优的几何构型等,均会为民用航空用户提供更优的空间信号质量以满足民航用户更高级别的需求,将来更贴合实际的BDS RAIM功能与性能有待进一步研究。
References)
[1] 吴云.GNSS接收机自主完备性监测算法研究[D].武汉:武汉大学,2009:16-18. WU Y.Algorithmresearch on GNSS receiver autonomous integrity monitoring[D].Wuhan:Wuhan University, 2009:16-18.
[2] 陈金平.GPS完善性增强研究[D].郑州:中国人民解放军信息工程大学,2001:68-72. CHEN J P.Research of GPS integrity augmentation [D].Zhengzhou:Information Engineering University, 2001:68-72(in Chinese).
[3] 中国卫星导航系统管理办公室.北斗卫星导航系统公开服务性能规范(1.0版)[S].2013:1-2. China Satellite Navigation Office.BeiDou navigation satellite system open service performance standard (Version 1.0)[S].2013:1-2(in Chinese).
[4] RTCA/DO-208.Minimum operational performance standards for airborne supplemental navigation equipment using global positioning system[S].Washington:RTCA SC-159 RTCA Inc.,July,1991.
[5] 刘瑞华,赵庆田,吕小平,等.“北斗区域导航系统”非精密进近导航性能分析[J].中国空间科学技术, 2015,35(4):53-59. LIU R H,ZHAO Q T,LV X P,et al.Performance analysis for BeiDou regional navigation satellite system of NPA[J].Chinese Space Science and Technology,2015, 35(4):53-59(in Chinese).
[6] TSO-C129.Airborne supplemental navigation equipment using the global positioning system(GPS)[S].Washington D.C.:FAA Aircraft Certification Service,Federal Aviation Administration,December 10,1992.
[7] 中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件(2.0版)[S].2013:4-6. CHINA SATELLITE NAVIGATION OFFICE. BeiDou Navigation Satellite System Signal In Space Interface Control Document Open Service Signal (Version 2.0)[S].2013:4-6(in Chinese).
[8] http:∥www.chinabeidou.gov.cn/xinwen/374.html
[9] ELLIOTT D KAPLAN,CHRISTOPHER J HEGARTY著,寇艳红译.GPS原理与应用[M].2版.北京:电子工业出版社,2012:240-243. ELLIOTT D.KAPLAN,CHRISTOPHER J.HEGARTY. Understanding GPS:principles and application[M].2nd ed. Beijing:Publishing House of Electronic Industry,2006:240-243(in Chinese).
[10] BROWN ALISON,STURZA MARK.The effect of geometry on integrity monitoring performance[C]∥Proceedings of the 46th Annual Meeting of The Institute of Navigation,Atlantic City,NJ,June, 1990:121-129.
[11] WU JYA-SYIN,NITIN PANDYA,JEFF LEWELLEN, et al.Non-precision approach availability sensitivity to GPS satellite constellation configuration[C]∥Proceedings of the 1999 National Technical Meeting of The Institute of Navigation.San Diego CA,January 1999:271-282.
[12] SHAOJUN FENG,WASHINGTON Y.OCHIENG, DAVID WALSH,et al.A measurement domain receiver autonomous integrity monitoring algorithm [J].GPS Solutions,2006,10(2):85-96.
[13] 杨鑫春,徐必礼,胡杨.北斗卫星导航系统的星座性能分析[J].测绘科学,2013,38(2):7-11. YANG X C,XU B L,HU Y.Performance research of constellation for COMPASS[J].Science of Surveying and Mapping,2013,38(2):7-11(in Chinese).
[14] 周富相,郑晓晶,刘培国.基于最小二乘残差的RAIM方案研究[J].通信技术,2011(3):44-45. ZHOU F X,ZHENG X J,LIU P G.Research on automatic integrity monitoring scheme of receiver based on least-squares residuals method[J].Communication Technology,2011(3):44-45(in Chinese).
[15] SU XIANLI,ZHAN XINGQUN,NIU MANCANG,et al.Receiver autonomous integrity monitoring availability and fault detection capability comparison between BeiDou and GPS[J].Journal of Shanghai Jiaotong University, 2014,19(3):313-324.
(编辑:车晓玲)
Simulation and research on RAlM algorithm built-in civil aviation airborne receiver based on BeiDou satellite systems
LIU Ruihua1,*,DENG Mingzhi1,YU Baoguo2,XING Zhaodong2
1.CollegeofElectronicInformationandAutomation,CAUC,Tianjin300300,China 2.The54thResearchInstituteofChinaElectronicsTechnologyGroupCorporation,Shijiazhuang050081,China
Receiver autonomous integrity monitoring(RAIM)algorithm is already mature in theory.But as to BeiDou navigation satellite system(BDS),there is rare analysis about the performance of RAIM with the observed data.According to the constellation status of BDS system and the performance of open service,based on the requirement of non-precision approach in civil aviation field,the simulation and research on RAIM were presented.Firstly,the availability of RAIM in Asia-Pacific was calculated.Then,the function and capability of failure detection and identification with the observed data from Nov Atel receiver were analyzed in different scenes and fault types.The simulation results show that the average of visible satellite is more than 7,and the HPL values are less than 500 meters.Furthermore, the measured research shows that the RAIM can detect the anomaly pseudo-range.That is to say,BDS system met the needs of the RAIM.The conclusion is that the BDS is suitable for RAIM,and can provide the required navigation performance(RNP)for non-precision approach (NPA)in the civil aviation field.
BeiDou satellite navigation system;integrity;BeiDou observed data;nonprecision approach;algorithm;simulation
TN967.1
:A
10.16708/j.cnki.1000-758X.2016.0022
2015-07-02;
:2015-12-23;录用日期:2016-02-24;< class="emphasis_bold">网络出版时间
时间:2016-04-19 15:30:09
http:∥www.cnki.net/kcms/detail/11.1859.V.20160419.1530.006.html
民航安全能力建设项目“北斗机载设备技术标准规定与应用研究”基金 (AADSA0007),中央高校基本科研业务费中国民航大学专项“基于北斗的通用航空指挥监控系统”基金 (20001006),“通用机载GNSS终端自主完好性技术研究”基金(KX142600033)
*
:刘瑞华(1965-),男,博士,教授、硕导,rhliu_cauc@163.com,主要研究方向为卫星导航、惯性导航和组合导航
刘瑞华,邓明智,蔚保国,等.基于北斗的机载终端完好性算法仿真研究[J].中国空间科学技术,2016,36(2): 20-27.LIURH,DENGMZ,YUBG,etal.SimulationandresearchonRAIMalgorithmbuilt-incivilaviationairborne receiverbasedonBeiDousatellitesystems[J].ChineseSpaceScienceandTechnology,2016,36(2):20-27(inChinese).
http:∥zgkj.cast.cn
