Harris-Laplace结合SURF的遥感图像匹配拼接方法
2016-02-13年华孙立于艳波
年华孙立 于艳波
(北京空间机电研究所,北京 100094)
Harris-Laplace结合SURF的遥感图像匹配拼接方法
年华孙立 于艳波
(北京空间机电研究所,北京 100094)
在遥感图像的处理和应用中,为了更好地解译、分析和研究图像信息,往往需要把两幅或多幅遥感图像拼接为一幅图像,文章针对遥感图像在旋转及受噪声影响时匹配困难的问题,提出了将Harris-Laplace(哈里斯-拉普拉斯)检测和SURF(快速稳健特征)算法相结合的匹配拼接方法。利用Harris-Laplace算法对遥感图像进行多尺度特征点检测,该特征点对光照变化、图像噪声和尺度改变具有不变性;然后,利用SURF算法确定特征点主方向并对特征进行描述;使用比值法进行初始匹配,接着用RANSAC(随机抽样一致性)算法剔除错误匹配点,并对匹配的图像进行拼接。试验结果表明,文中方法不但具有很好的抗旋转性能和抗噪声性能,而且较经典的SIFT(尺度不变特征变换)算法提高了匹配效率,能够为遥感图像的实时配准拼接以及几何定位精度评价提供有力的技术支持。
哈里斯-拉普拉斯检测 尺度不变特征 快速稳健特征算法 特征提取 遥感图像匹配
0 引言
图像配准是指同一目标的两幅(或者两幅以上)图像在空间位置的对准。图像配准技术过程,称为图像匹配或者图像相关。常用的算法主要分为两类:基于灰度的图像匹配方法和基于特征的图像匹配方法。基于特征的图像匹配方法可以克服基于灰度的图像匹配方法对于发生缩放或旋转的图像匹配精度低的缺点,因而在图像匹配领域得到了广泛的应用。基于特征的匹配方法包含特征提取和特征匹配两个阶段。前一个阶段主要完成整幅图像中的特征点及其属性的提取(角点、顶点、边缘、直线等),后一阶段则是对提取的特征进行匹配,通过匹配的特征建立图像间的映射变换得到匹配图像,其中前一阶段的结果(提取的特征和属性)决定后一阶段的精度和可信度[1]。目前基于特征提取算法主要有Forstner(福斯特纳)[2]、SUSAN(最小核值相似区)[3]、Harris角点[4-5]、SIFT(尺度不变特征变换)[6]、SURF(快速稳健特征)[7]等。其中,Harris角点是C.Harris和M.J.Stephen于1988年对Moravec(莫拉维克)算子[4]做出改进继而提出的一种检测算法,Mikolajczyk和Schmid又在Harris检测基础上提出了具有尺度不变性能的Harris-Laplace[8]检测。SIFT算法最早由David. G. Lowe于1999年提出,并在2004年进行了完善[9],该算法是一种鲁棒性很好的尺度不变特征算法,可以处理两幅图像之间发生平移、旋转、尺寸变化、光照变化情况下的特征匹配问题,在一定程度上对视角变化、仿射变化也具备较为稳定的特征匹配能力,是公认有效的算法。李晓明等将SIFT算法应用到遥感影像的自动匹配[10],取得了较好的效果。然而SIFT算法耗时长,很难满足实时应用的要求,因此很多人对它进行了改进。Ke和Sukthankar提出将PCA(主成分分析)应用到图像梯度中,得到了PCA-SIFT算法[11],改进后的算法对特征进行了降维处理,从而简化了SIFT算法的复杂度。2006年,Bay等人以SIFT算法为基础提出了SURF算法,该算法不但具有尺度和旋转不变性,而且在特征信息描述方面表现出了更好的性能,并且在计算速度上有明显优势,综合性能要优于SIFT算法。
在遥感图像数据处理中,图像匹配是变化检测、数据融合的基本预处理步骤,匹配精度对后续数据的处理产生重要的影响[12]。遥感图像几何质量参数的评价也都是通过控制点选取并进行同名点位置匹配完成的[13]。遥感图像在获取的过程中,受到大气吸收与散射、传感器标定、地形等因素影响,因此拍摄的图像不仅受噪声的影响,而且存在灰度差异或几何畸变等,这使得遥感图像的匹配过程比较困难。针对以上问题,本文结合Harris-Laplace检测算法和SURF算法的稳定性,提出了一种特征提取方法,以Harris-Laplace检测为特征点,以SURF算法进行特征算子描述,从而实现了遥感图像的匹配和拼接。通过实验并与经典SIFT算法进行比较,得出该算法在匹配精度和速度上的综合性能优于SIFT算法,尤其在抗噪声性能方面有明显的优势。
1 本文算法
基于特征的图像匹配与拼接一般分为特征点检测、特征点描述、特征描述子之间的匹配、图像融合4个步骤。如何获得稳健、性能良好的特征点也就成为匹配拼接图像处理的关键基础。
在特征点检测方面,要求获取的特征点不但含有丰富的图像信息特征而且具有优良的性能。目前已有的成熟特征点检测算法中,Harris角点具有旋转不变性,对于图像亮度和对比度变化不敏感,然而它不具有尺度不变性;SURF基于Hessian矩阵的特征点检测过程对图像二阶偏微商进行了近似估算以及非极大值抑制,这会使图像特征点损失掉很多高频信息且只能获得数量较少的特征点。将Harris检测和高斯尺度空间结合的Harris-Laplace特征点检测,在位置可重复性、定位精确度、尺度不变性等方面均有较好的性能,不但能够保留图像中重要特征信息而且提取的算法简单。
在特征点描述方面,特征描述子应当能给特征点指定方向,具有旋转不变性、尺度不变性以及噪声鲁棒性。二值化描述子通过对特征点邻域内的灰度进行比较生成,计算量小,但是在有较多相似特征的情况下错误匹配率高;SURF算法采用均匀方向标准化的正方形区域中的点生成64维特征描述子,包含的信息更加丰富,具有更强的可区分性。
本文针对上述研究分析,考虑使用具有尺度不变性的Harris-Laplace角点取代SURF算法中数量较少的极值特征点,这样既保留了SURF优良的特征描述性能,又弥补SURF算法中特征点少且损失了高频信息的不足,保证了足够数量的匹配点,从而提高遥感图像匹配精度。本文的算法流程如图1所示。
1.1 特征点检测
1.1.1 尺度空间
尺度空间理论是检测不变特征的基础,主要讨论信号平滑处理的问题。Lindeberg证明了高斯卷积核是实现尺度变换的唯一变换核[14]。

图1 本文算法流程Fig.1 Algorithm flow chart
一幅二维图像在不同尺度下的尺度空间函数L( x, y,σ)可由输入的原始二维图像I( x, y)与高斯核函数G( x, y,σ)卷积得到:

式中 (x,y)为尺度空间下的笛卡尔坐标;σ为高斯核函数G( x, y,σ)正态分布的方差,又称尺度空间因子。高斯核函数G( x, y,σ)的计算公式为

式中, 尺度空间因子σ反映了图像被平滑的程度,其值越小表征图像被平滑程度越小,相应尺度也越小。
1.1.2 Harris-Laplace检测
Harris-Laplace检测算法实现流程如下:
1)二阶矩阵表征了一个点在邻域内的梯度分布[15],使用高斯核函数对多尺度二阶矩做加权,计算Harris二阶矩阵:

式中 方阵μ(x, y,σI,σD)表示Harris二阶矩阵;σI为积分尺度因子,是决定角点当前尺度的变量;σD为微分尺度因子,是决定角点附近微分值变化的变量;g(σI)表示积分尺度σI的高斯卷积核;g(σD)表示微分尺度σD的高斯卷积核;Lx(x, y,σD)和Ly(x, y,σD)表示对图像使用g(σD)进行平滑后再在x和y方向进行一阶微分的结果,Lx(x, y,σD)=I( x, y)*Gx(x, y,σD),Ly(x, y,σD)=I( x, y)*Gy(x, y,σD),其中Gx(x, y,σD)和Gy(x, y,σD)分别表示尺度因子为σD时高斯核函数在x、y方向上的一阶微分。
2)计算每一层尺度上每个像元的Harris的响应值:

式中 detμ(x, y,σI,σD)为方阵μ(x, y,σI,σD)的行列式;trμ(x, y,σI,σD)为方阵μ(x, y,σI,σD)的迹;α为经验值,一般取0.04~0.06的常数。
3)利用LoG(Laplacian of Gaussian,高斯拉普拉斯)函数对角点进行筛选[16],对小于某个阈值的响应值置为零:
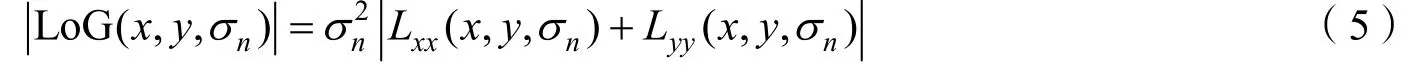
式中 Lxx和Lyy表示L(x,y,σn)在x和y方向上的二阶微分;σn为给定的尺度空间值。
4)以该点为中心点,在其“8-邻域”[17]内求极大值,并与该点Harris的响应值进行比较,较大者选作检测点。

图2 主方向的确定(滑动窗口围绕特征点转动)Fig.2 Orientation assignment (a sliding orientation window detects around the feature points)
1.2 特征点描述
1.2.1 主方向确定
为使特征点具有旋转不变性能,必须为每个特征点寻找一个主方向。本文使用Haar小波的响应来确定特征点的主方向。首先以特征点为圆心,在半径为6σ(σ为特征点尺度因子)的圆形邻域内计算x和y方向的Haar小波响应dx和dy。为了获得主方向,设计一个角度为π/3的滑动窗口,如图2。通过滑动窗口对整个圆形区域的遍历,计算该窗口处于每个角度时它所包含图像点的Haar小波响应之和,统计每一点x、y方向的响应,则滑动窗口中所有点的响应之和构成一个矢量,其中最长矢量对应的方向即为特征点主方向。
1.2.2 构建特征描述子
构建特征描述子就是建立特征向量的过程。首先以特征点为中心构建一个20σ×20σ的矩形区域。沿着特征点的主方向,将矩形区域划分为44×的子区域,在每块子区域中计算x和y方向的Haar小波响应,用dx表示水平方向的响应,用dy表示垂直方向的响应,并对响应以及响应的绝对值进行累加和统计。由此,每个子区域有了4维的强度结构描述向量:

这样,计算所有44×子区域,结果就是64维的描述向量,如图3所示。该向量就是描述此特征点的描述子特征向量。图4给出了三种图像强度明显不同的子区域的描述子属性。其中,第一幅灰度均匀,所有强度结构的值都比较低;第二幅灰度在x方向上交替变化,则∑|dx|的值较大,其他值都比较小;第三幅灰度在x方向上逐渐加强,则∑|dx|和∑|dy|的值都较大,其他值比较小。可以看出,通过这种4维结构的描述向量能够产生具有良好鉴别力的特征描述子。
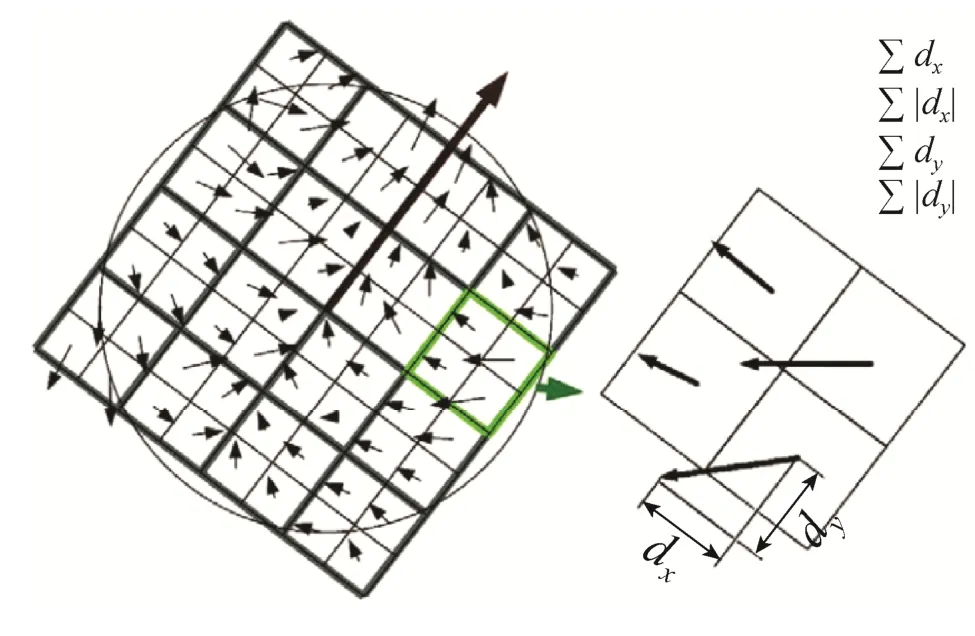
图3 特征描述子的生成Fig.3 Feature descriptor extraction

图4 三种基本图像子区域的特征描述子Fig.4 The descriptor entries of a sub-region of the underlying intensity pattern
1.3 特征点匹配
特征点的匹配是特征描述子之间相似度的度量[18],本文通过最近邻与次近邻的比值来作为度量。计算两个特征点描述子之间的欧式距离,找出与特征点描述子pi欧式距离最邻近的特征点描述子pj和次邻近的特征点描述子pk,pi与pj以及pi与pk两组描述子之间的欧式距离分别为并计算它们的比值若比值r小于规定阈值则视为匹配成功,点(pi, pj)则为图像中的一对匹配点,本文根据经验值定义阈值为0.7。由于遥感图像中包含大量相似的结构,分布在相似结构中的点有可能发生误匹配,本文采用RANSAC(随机抽样一致性)算法对错误匹配的特征点进行剔除[19],从而得到特征匹配点对。
2 试验结果与分析
为验证本文方法的有效性和可靠性,选取两组数据进行测试分析,操作系统Windows XP,开发环境为MATLAB R2009a。第1组两幅待匹配图像采用我国首颗民用高分辨率立体测绘卫星“资源三号”[20]拍摄的迪拜棕榈岛遥感影像作为测试数据,并对其中一幅进行了旋转,用以测试特征描述子的抗旋转性能。第2组两幅待匹配图像采用自主研制的“资源一号”02C卫星相机拍摄的日本名古屋地区遥感影像作为测试数据,并在两幅图像中添加入了随机椒盐噪声,用以测试特征描述子的抗噪声性能。用本文提出的方法完成匹配并与经典SIFT算法的匹配性能进行比较,得到的遥感图像特征匹配试验结果见图5和表1。

图5 遥感图像特征匹配Fig.5 Remote sensing image feature matching

表1 遥感图像匹配试验数据Tab.1 The matching results based on different methods
由以上两组试验结果可以看出,对于经过旋转的第1组图像,SIFT算法和本文算法的抗旋转性能都很好,不同算法提取的特征均能达到较好的匹配效果,本文算法的匹配精度略优于SIFT算法。对于加入噪声的第2组图像,本文算法抗噪性能要明显优于SIFT算法,SIFT算法出现了比较多的误匹配,本文算法的所提取的特征具有更强的鲁棒性;在匹配速度方面,本文算法的匹配耗时比SIFT算法少近1/2。可见本文算法在特征匹配的精度和速度上均优于SIFT算法。
在完成匹配的基础上,进一步对图像进行拼接试验,图6的拼接结果构造了一幅视觉可行的全景图,颜色和结构都能在图像间自然过渡。在拼接缝附近,两幅图像色调或纹理上没有明显的拼接缝,并且图像之间的重叠区域没有突变,过渡自然。

图6 遥感图像拼接结果Fig.6 Remote sensing image mosaic result
3 结束语
本文在研究了Harris-Laplace检测以及SURF算法特征提取的基础上,提出了将二者结合的方法应用到遥感图像匹配拼接中。采用具有尺寸不变性的Harris-Laplace作为特征点,以SURF描述子进行特征构建,并利用RANSAC算法进行提纯,该方法弥补了SURF特征点较少且损失了图像高频信息的不足。通过两组试验并与经典传统算法进行比较,可以看出本文算法具有很好的抗旋转性能和抗噪声性能,在特征匹配的精度和速度上均优于SIFT算法,并且能够达到良好的拼接水平。
References)
[1] 吕江安, 于晋, 陈琦. 基于SIFT特征的三线阵CCD影像立体匹配[J]. 航天返回与遥感, 2010, 31(2): 38-45. LYU Jiang’an, YU Jin, CHEN Qi. Stereo Matching of Three-line CCD Imagery Based on SIFT[J]. Spacecraft Recovery &Remote Sensing, 2010, 31(2): 38-45. (in Chinese)
[2] FOROOSH H. Extension of Phase Correlation to Subpixel Registration[J]. IEEE Transactions, 2002, 11(3): 188-200.
[3] SMITH S M, BRADY J M. SUSAN: A New Approach to Low Level Image Processing[J]. Journal of Vision, 1997, 23(1): 45-78.
[4] HARRIS C G, STENHENS M J. A Combined Corner and Edge Detector[C]//Proceedings of 4th Alvey Vision Conference Manchester: ICASSP, 1988: 147-152.
[5] 王崴, 唐一平. 一种改进的Harris角点提取算法[J]. 光学精密工程, 2008, 16(10): 1995-2000. WANG Wei, TANG Yiping. An Improved Algorithm for Harris Corner Detection[J]. Optics and Precision Engineering, 2008, 16(10): 1995-2000. (in Chinese)
[6] LOWE D G. Object Recognition from Local Scale-invariant Features[C]//Proceedings of 7th IEEE International Conference on Computer Vision. Corfu, Greece, 1999, 2: 1150-1157.
[7] BAY H, ESS A, TUYTELAARS T. SURF: Speeded Up Robust Features[J]. Computer Visio and Image Understanding, 2008, 110(3): 346-359.
[8] MIKOLAJCZYK K, SCHMID C. An Affine Invariant Interest Point Detector[C]//European Conference on Computer Vision, 2002, 2350: 128-142.
[9] LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110.
[10] 李晓明, 郑链, 胡占义. 基于SIFT特征的遥感影像自动配准[J]. 遥感学报, 2006, 10(6): 885-892. LI Xiaoming, ZHENG Lian, HU Zhanyi. SIFT Based on Automatic Registration of Remotely-sensed Imagery[J]. Journal of Remote Sensing, 2006, 10(6): 885-892. (in Chinese)
[11] YAN K, SUKTHANKAR R. PCA-SIFT: A more Distinctive Representation for Local Image Descriptors[C]//Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, DC: USAIEEE Computer Society, 2004: 511-517.
[12] TOWNSHENG J R G, JUSTIC C O, GUMEY C, et al. The Impact of Misregistration on Change Detection[J]. IEEE Trans on Geo-sciences and Remote Sensing, 1992, 30(5): 1054-1060.
[13] 陈艺虾. 遥感图像几何定位精度评价方法研究[D]. 南京: 南京理工大学, 2013. CHEN Yixia. Research on Remote Sensing Image Geometric Positioning Accuracy Evaluation[D]. Nanjing: Nanjing University of Science and Technology, 2013. (in Chinese)
[14] LINDEBERG T. Scale-space Theory: a Basic Tool for Analysing Structures at Different Scales[J]. Journal of Applied Statistics, 1994, 21(2): 224-270.
[15] MIKOLAJCZYK K, SCHMID C. Indexing Based on Scale Invariant Interest Points[C]//Proceedings of the 8th International Conference on Computer Vision, 2001: 525-531.
[16] ZITOVA B, FLUSSER J. Image Registration Methods: A Survey[J]. Image and Vision Computing, 2003, 21(5): 977-1000.
[17] PRATT W K. Digital Image Processing[M]. 3rd ed. New York: Wiley Inter-science, 1991.
[18] 杨占龙. 基于特征点的图像配准与拼接技术研究[D]. 西安: 西安电子科技大学机电工程学院, 2008. YANG Zhanlong. Research on Image Registration and Mosaic Based on Feature Point[D]. Xi’an: School of Electro-mechanical Engineering, Xidian University, 2008. (in Chinese)
[19] FISCHLER M A, BOLLES R C. Random Sample Consensus: a Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Communications of the ACM, 1981, 24(6): 381-395.
[20] 高卫军, 孙立, 王长杰, 等. “资源三号”高分辨率立体测绘卫星三线阵相机设计与验证[J]. 航天返回与遥感, 2012, 33(3): 25-34. GAO Weijun, SUN Li, WANG Changjie, et al. Design and Verification of Three-line Array Camera for ZY-3 High Resolution Stereo Mapping Satellite[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(3): 25-34. (in Chinese)
Remote Sensing Image Matching and Mosaic Based on Harris-Laplace Combined with Scale-Invariant Algorithm
NIAN Hua SUN Li YU Yanbo
(Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China?)
In the area of remote sensing image application, two or more images are usually mosaiced as one image. According to remote sensing image matching, a method of image matching and mosaic based on Harris-Laplace combined with SURF algorithm is proposed in this paper. Firstly, feature points are detected by using Harris-Laplace in multiple scales, which has the capability of invariance to illumination changes, image noise and scale changes. Then, by calculating with SURF algorithm, the main directions of the feature points are determined and the feature descriptors are generated. Ratio method is used to get initial matching, and RANSAC algorithm is used to eliminate errors and achieve accurate matching, then the image mosaicing completed. The experiment results show that the method proposed has good anti-rotation and anti-noise performance, and improve the matching efficiency obviously compared with the classical SIFT algorithm. The method can be well applied in the remote sensing image processing and geometric positioning accuracy evaluation.
Harris-Laplace detection; scale-invariant; speed up robust features algorithm; feature extraction; remote sensing image matching
TP751.1
A
1009-8518(2016)06-0095-07
10.3969/j.issn.1009-8518.2016.06.011
年华,女,1982年生,2009年获西北工业大学信号与信息处理专业硕士学位,工程师。主要从事光学遥感相机研制等工作。E-mail: joyfulnh@163.com。
(编辑:夏淑密)
2016-06-03
