基于遗传算法的移动机器人路径规划方法

张健

（安徽三联学院计算机工程学院，安徽合肥230001）

基于遗传算法的移动机器人路径规划方法

张健

（安徽三联学院计算机工程学院，安徽合肥230001）

机器人路径规划是机器人领域的一项重要课题，不同于以往在遗传算法过程中考虑路径平滑度的方法，本文提出了一种将遗传算法过程与路径平滑过程分开的机器人路径规划新方法。先设计可变长编码方式的简单遗传算法产生较优的折线路径，再引入一类新的带形状参数的回旋螺线对其进行平滑操作，以抚平较大转角。整个路径规划过程，只需输入障碍物坐标即可自适应地选择参数以产生机器人行走路径。仿真结果表明，将遗传算法过程与路径平滑过程分离的做法能降低遗传算法本身复杂度，所以设计的平滑操作不仅提高了路径平滑度，还可以减少路径长度。

移动机器人；遗传算法；回旋螺线；平滑操作；路径规划

机器人路径规划是机器人领域的一项重要课题，它实际上是一个复杂的非线性规划问题，主要解决在含有障碍物的环境中为机器人寻找一条从起点到终点的无碰行走路径的问题，该路径应满足长度短、使用时间少、平滑度高等标准。机器人路径规划方法的好坏对机器人的安全性及工作效率等起到至关重要作用。目前机器人路径规划的方法有图搜索法、Dijkstra算法[1]、人工势场法等，这些算法都有各自的优点，但是总体来说还存在着适应性低、算法复杂高等问题。作为优化算法的一种，遗传算法[2]在机器人路径规划这类复杂的非线性优化问题中显示出很好的鲁棒性，已得到了广泛应用。该算法虽然定义了平滑、截断等遗传操作，能局部调整机器人行走路径的转角，有效考虑了路径的平滑度问题，但在不同程度上增加了遗传算法本身的复杂性。因此，引入回旋螺线，将遗传过程与平滑操作分开，达到提高路径平滑度、缩短路径长度的要求，也减小遗传算法本身复杂度。

1 回旋螺线相关问题

1.1 回旋螺线

回旋螺线[3]是一种用Fresnel积分构造的平面曲线，它的曲率与弧长成正比。这里引入一种带形状参数λ（0≤λ≤1）的推广的Fresnel积分，利用这种积分构造的回旋螺线，当λ=0.5时即成为标准的回旋螺线。

定义1曲线

称为推广的回旋螺线，简称回旋螺线，其中比例因子α为正数，形状因子0≤λ≤1,θ表示切角变差，C（θ；λ）及S（θ；λ）为带形状参数λ的推广的Fresnel积分，

1.2 回旋螺线偶[3]

定义2回旋螺线偶是由两条回旋螺线

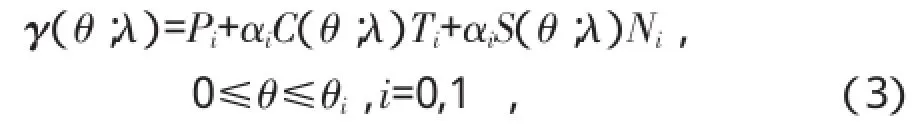
组合而成，其中Pi（i=0,1）是它们的起点，αi是起点处的比例因子，Ti是起点处的单位切向量，Ni是起点处的单位法向量。要求这两条回旋螺线之间保持G2连续，即它们的终点重合，且终点处的切向量平行，不带符号的曲率相等。

2 基于遗传算法与回旋螺线的机器人路径规划新算法

传统的遗传算法在提高机器人路径平滑性问题上，多数采取改写适应度函数或增加遗传操作的方法。为了降低遗传算法本身的复杂性，灵活调整路径中的转角，提出了将平滑过程与遗传算法过程分开的做法，下面将分别进行详细讨论。

2.1 遗传算法描述

将机器人简化为质点，假设障碍物为凸多边形。将障碍物的各边界向外扩张一定的安全距离，形成新的障碍物，这样即使路径与新障碍物的某顶点重合，实际上也与原障碍物保持有安全距离。

（1）编码方式

所谓编码是指将问题的解空间转换到遗传编码空间的过程。编码对于算法的种群多样化和搜索能力等性能有较大的影响，对于机器人路径规划问题，本文采取浮点数变长编码方式，染色体[4]由路径节点的笛卡尔坐标序列构成。一系列点的连接构成了染色体，表示是一条可行或者不可行路径。

（2）种群初始化

遗传算法的种群初始化过程有很多种，在研究该算法时，通常随机产生初始化种群，该方式生成的初始种群优点是适用于任何问题，不依赖于某个具体问题，缺点是无法确保种群的合理性，算法的高效性也无法确定。本文采用的是在随机产生初始种群方式的基础上增加启发式方法，这样既能提高路径生成的效率，又能较科学地体现解空间的信息。

初始种群产生步骤：

step1染色体的个体包含的中间点个数（包含坐标）均是随机产生；

step2已知路径中的起点和终点，在无障碍物情况下，该路径是距离最短、最平滑，借助这一信息可以启发式地产生个体中的其他中间点，达到提高算法的搜索效率。

（3）适应度函数[5]

在前面的障碍物为凸多边形环境表示中已将障碍物边界向外扩充一定的安全距离，且后文还将引入回旋螺线偶对路径进行平滑操作，故适应度函数只需包括路径的长度以及判断是否与障碍物相碰。适应度函数为

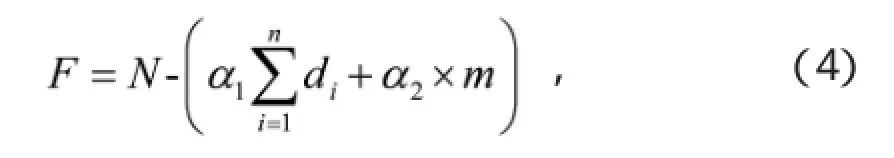
（4）遗传操作

1)选择算子：采取轮盘赌方法实现选择操作。

2)交叉算子：采取单点交叉的方法。由于是变长编码，故两个染色体的交叉可以不在同一位置。若新产生的个体长度超过了染色体长度上限，则舍去。

3)变异算子：个体以一定的概率进行变异，范围为整个空间，以增加种群多样性。

（5）遗传算法终止条件

1)在进化过程中适应度函数具有最大适应度个体作为最优解输出，则算法终止。

2)种群的适应度和最优个体适应度不再增加时，则算法终止。

3)迭代次数达到预设的代数时，预设代数一般设置在100~500代，则算法终止。

2.2 基于回旋螺线的平滑操作

为了保证机器人转弯时的安全性，在适应度函数中增加了路径平滑度的遗传算子[6]，若一条路径中所有节点的转角之和较大，则降低其适应度，从而使该条路径更容易被淘汰。该方法有效地考虑了路径平滑度的问题，以较高的效率生成一条较优的无碰折线路径。

现在引入一种带形状参数的推广的回旋螺线，对已产生较优的无碰折线路径进行平滑操作，通过自适应地选择形状参数，从而生成最终平滑的路径。先介绍在单个节点处引入回旋螺线的平滑操作，然后介绍多个节点处的平滑操作。

为了简化遗传算法，以较高的效率得到一条较优的无碰折线路径，前面所述的遗传过程中暂时省去了路径平滑度的考虑，此时的路径可能含有较大的转角，如图1中的角α及β。根据机器人的具体情况预先设定一个安全转角，依次判断此路径上的各个节点处的转角大小，当超过预定的安全角度时，本文将引入上述推广的回旋螺线偶对其进行平滑操作。

图1 折线路径中的大转角

不妨设Pi点处转角α超过了安全角度，需要对该点进行平滑操作。如图2，在Pi及其相邻的两个节点的连线上选取中点A和B，将A、Pi、B等3个点看作控制顶点，选择形状参数λ，生成回旋螺线偶作为新路径代替原有折线路径。这样，就达到平滑转角的目的，同时也缩短了路径长度。

图2 大转角处的平滑操作

若生成的回旋螺线偶碰撞了障碍物，需对其进行调整。由于受λ=0.5的限制，通过移动控制点来避开障碍物，无需移动任一控制点，只需增大形状参数λ的值就可以使回旋螺线偶更贴近控制多边形，从而控制其避开障碍物。需要注意的是，形状参数λ越大时，回旋螺线偶越贴近原折线路径，不利于机器人的转弯安全。从这一角度考虑，形状参数λ应越小越好，且此时路径长度也会缩短。然而，当λ过小时，回旋螺线偶远离控制多边形，很可能碰撞障碍物。故在操作时，令λ（0≤λ≤1）取值从初始值0.1开始，以步长0.1增加，自适应地选取形状参数λ的值，使其满足定义1条件且产生的路径不碰撞障碍物的最小值。

当路径中含有多个较大的转角时，依次对每个转角进行平滑处理。如图3所示，不妨设Pi及Pi+1处转角均超过了安全角度，分别对他们进行平滑操作。Pi点处的平滑操作与上述相同，下面对Pi+2点进行平滑操作。在Pi+1及Pi+2连线上选取中点C，以B、Pi+1、C为控制点生成回旋螺线偶代替原有Pi+1点处的折线路径。

作为圆弧与圆弧、直线与直线或圆弧与直线之间的过渡曲线，回旋螺线偶与控制多边形相结合生成的样条曲线能达到G2连续。所以回旋螺线偶可以很好地嵌入到遗传算法得到的折线路径中，使新产生的路径能保持较高连续性。同时，每个转角处的平滑操作相互独立，即它们的形状参数可以独立取值，这样可以通过形状参数来局部调整路径的形状，灵活方便。此平滑操作能有效提高机器人转弯时的安全性，也缩短了原有折线路径的长度[7]。

图3 多个转角的平滑处理

3 仿真实验及结果分析

3.1 不同环境下的仿真实验

本文设计的路径规划方法，只需输入环境坐标，就可以自适应地得到最终的平滑路径。为了验证算法的有效性，下面分别在特殊障碍物、规则障碍物和不规则多障碍物的环境中分别进行了3组仿真实验。

特殊障碍物环境如图4所示，其中3个长条状物体为障碍物，机器人的起点为（0，50），终点为（100，50），此环境虽然障碍物稀少，但障碍物较大且分布独特。图5为规则的多障碍物环境，图中排列有序的小正方形为一个个障碍物，机器人起点为（0，30），终点为（100，80），此环境中障碍物分布均匀，但数量较多。图6为不规则的多障碍物环境，图中散乱的多边形为一个个障碍物，机器人起点为（0，0），终点为（100，100），此环境中障碍物形状不规则、分布杂乱、且数量较多。

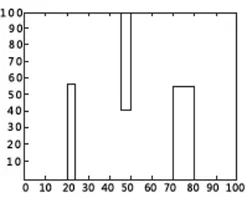
图4 特殊多障碍物环境图

图5 规则多障碍物环境

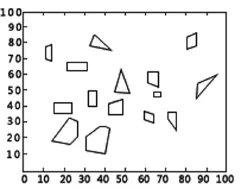
图6 不规则多障碍物环境

特殊障碍物环境中的仿真实验。由于障碍物的特殊性，传统的单纯基于遗传算法的路径规划方法所得路径难免有较大转角。图7的折线即为本文遗传算法部分得到的机器人避障行走路径，包含节点P1，P2，P3，P4，P5，其中P2，P3及P4的转角均超过了预定的安全角度90度，应对它们进行平滑操作。如图8所示，取P1，P2的中点A，取P2，P3的中点B，取P3，P4的中点C，取P4，P5的中点D，以A，P2，B为P2处的控制点，以B，P3，C为P3处的控制点，以C，P4，D为P4处的控制点，分别对各点自适应地选取形状参数，λ（0≤λ≤1）从0.1开始，以步长0.1增加。经计算，当3个节点的形状参数分别取λ=0.7，λ=0.5，λ=0.3时，均为首次满足定义1中回旋螺线偶生成条件的最小形状参数。图8中曲线即为各节点处首次生成的回旋螺线偶，虚线为控制多边形，即原有折线路径。

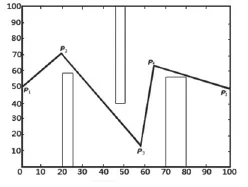
图7 遗传算法所得折线路径

经计算发现，此时P2及P3点处首次生成的回旋螺线偶已经能够避开障碍物，故不再增加其形状参数的取值。而P4点处当λ=0.3时虽然满足回旋螺线偶生成条件，但所产生的路径会碰撞障碍物，需要继续增加λ的取值。经计算，直至λ=0.5时，生成的回旋螺线偶不碰撞障碍物，如图9，故最终取P4的形状参数为λ=0.5。

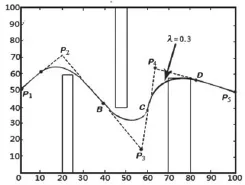
图8 自适应选择参数过程

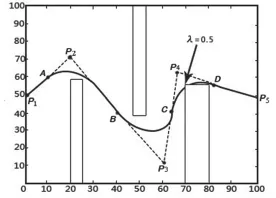
图9 最终的平滑路径

在第2组规则多障碍环境中进行路径规划仿真实验，该仿真实验过程与第1组的实验过程相同。如图10，折线为遗传算法部分得到的路径，包含节点P1，P2，P3。曲线为对P2点进行平滑操作后产生的回旋螺线，其控制点为P2，P1P2的中点A和P2P3的中点B，最终自适应选取P4形状参数为λ=0.4。

图10 规则多障碍物环境下最终的平滑路径

同理，在第3组不规则多障碍物环境中的仿真实验过程与前两组相同。如图11，最终自适应选取P4形状参数为λ=0.6。

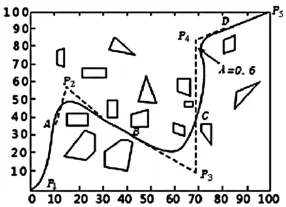
图11 不规则多障碍物环境下最终的平滑路径

由上述仿真结果可以明显看出，在3种不同的障碍物环境中，利用回旋螺线偶对折线路径进行平滑操作后，都达到了平滑路径的效果，路径总长度也得到一定程度的缩短。特别是在第1组仿真结果的特殊障碍物分布情形下，克服了传统遗传算法中大转角问题。同时，也降低了遗传算法本身的复杂度。

3.2 与Dijkstra算法的比较

将本文所提出的遗传算法过程与路径平滑过程分开的方法与基于Dijkstra算法的路径规划方法进行比较，在上述3组不同环境中进行的多次实验结果表明，本文提出的路径规划方法得到的最优路径长度小于基于Dijkstra算法的得到的最优路径长度，且所使用的平均搜索路径时间小于基于Dijkstra算法使用的平均搜索路径时间，至少可以节约5%的搜索时间。

通过上述比较，发现遗传算法过程与路径平滑过程分开的方法在时间复杂度上优于Dijkstra算法，在解决路径规划问题方面有一定的优势。

4 结束语

传统的遗传算法在提高机器人路径平滑性的问题上，多数采取改写适应度函数或增加遗传操作的方法，本文则采用遗传算法过程与路径平滑过程分开的办法。遗传算法产生较优路径后，引入一种新的带形状参数的回旋螺线偶对其进行平滑操作。整个路径规划过程只需输入障碍物坐标就可以自适应的选择参数生成平滑的路径，且只需改变形状参数就可以灵活调节路径与障碍物坐标距离。仿真结果表明，引入回旋螺线将遗传过程与平滑操作分开的方法能达到提高路径平滑度、缩短路径长度的要求，同时也减小了遗传算法本身的复杂度。

[1]孙自广，李春贵，王秦.基于改进遗传算法的机器人路径规划[J].自动化与仪表，2009，24（6）：5-7.

[2]李良先.自主型足球机器人路径规划与避障策略研究[D].焦作：河南理工大学，2011.

[3]郝博，秦丽娟，姜明洋.基于改进遗传算法的移动机器人路径规划方法研究[J].计算机工程与科学，2010，32（7）：104-107.

[4]石铁峰.改进遗传算法在移动机器人路径规划中的应用[J].计算机仿真,2011，28（4）：193-195.

[5]廖卫强,李振宇.基于遗传势场法的足球机器人路径规划[J].集美大学学报（自然科学版），2009，14（2）：179-184.

[6]浦定超.基于遗传算法的移动机器人路径规划的研究[D].合肥：合肥工业大学，2010.

[7]李刚，鱼佳欣，郭道通,等.基于改进遗传算法的机器人路径规划与仿真[J].计算技术与自动化，2015（2）：24-27.

Path Planning Method for Mobile Robot Based on Genetic Algorithm

ZHANG Jian
(School of Computer Engineering，Anhui Sanlian University，Hefei，Anhui 230001，China)

Robot path planning is an important topic in the field of robotics.Considering the path different from the past in the smoothness of the process of genetic algorithm method,a genetic algorithm process is presented by smoothing the path separate from the new path planningmethod.After calculating a path using simplified GAmethod with a variable length coding, a new type of clothoid curvewith wipe parameter is introduced to smooth the sharp turns.In the entire path planning process, the parameter can be chosen adaptively to generate a robot’s walk path as soon as the barrier’s coordinate is entered.The simulation results show that the method of separating smooth process from GA process simplifies GA method.The proposed method can efficiently decrease the path length aswell as increase the path smoothness.

mobile robot；genetic algorithm；cyclotron curve smooth；path planning

TP242

A

1007-4260(2016)04-0048-05

时间：2017-1-3 17:19

http://www.cnki.net/kcms/detail/34.1150.N.20170103.1719.014.html

2016-03-14

安徽省教育厅高校自然科学研究项目(KJ2013B090)和安徽三联学院2016年度校级科研基金（xtcx2016002）。

张健，男，安徽泗县人，硕士，安徽三联学院计算机工程学院讲师，研究方向为无线传感器网络。

E-mail:626742382@qq.com

10.13757/j.cnki.cn34-1150/n.2016.04.014