基于MATLAB的土体三轴试验抗剪强度指标求解计算

马 勇， 王 飞， 杜秀忠

(广东省水利水电科学研究院，广东省岩土工程技术研究中心，广东 广州 510635)

基于MATLAB的土体三轴试验抗剪强度指标求解计算

马 勇， 王 飞， 杜秀忠

(广东省水利水电科学研究院，广东省岩土工程技术研究中心，广东 广州 510635)

莫尔应力圆通常是利用作图的方法获得，进而求得岩土体的强度指标，但该方法易受人为影响，精度较低。通过MATLAB软件编制相应的计算程序求得岩土体的强度指标，该软件是基于最小二乘法原理，对最大主应力和最小主应力的线性回归方程进行求值，进而通过抗剪强度指标与最大主应力和最小主应力的关系反算求得c、φ值。通过相关文献数据，验证本文方法的准确性和可靠性，为岩土体抗剪强度指标值的计算提供了一条新的解决途径。

三轴试验；抗剪强度指标；MATLAB；最小二乘法

计算岩土体抗剪强度有许多种方法[1-2]，三轴压缩试验是测定岩土体抗剪强度的一种常用的试验方法，试验时，通常利用多个一定规格的圆柱形试验样品，在保持一定的围压下分别进行轴向压力的施作，对试样进行剪切试验直至试样破坏，获得试样在不同围压状态下的极限轴向压力，不同的轴向压力和相对应的围压也分别称为大、小主应力。然后，对获得的数据根据强度准则[3]进行拟合处理，得出试样的破坏包络线，进行求得试样的岩土体强度参数。试验数据处理时，由于计算绘图工作量大，需要做大量的重复性工作，且作图法亦会引入一些人为误差，随意性较大。为了得到较为准确的抗剪强度值，目前抗剪强度指标的求解主要是在试验数据的基础上采用较严谨的强度理论进行推导或利用软件分析，以减少手工作图产生的随意误差[4]。阮波等[5]基于非线性规划方法，利用EXCEL软件对三轴剪切试验的破坏包络线直接进行规划求解，进而获取了试样的抗剪强度参数值。李小磊等[6]通过软件对Matrix VB的功能进行调用，利用合理的程序设计，基于最小二乘法原理对摩尔应力圆的切点进行线性回归，进而求解得到抗剪强度指标值。王星辉[7]基于严格的理论推理，采用数据直接计算的方法来替代以前手工作图或计算机交互图解，取得了较好的效果。三轴剪切试验的破坏包络线也可以采用CAD作图的方法来绘制，但其绘图的效率和精度均不理想，而且也无法直接获得强度参数值，更由于个人的经验和误差的原因，得到的强度参数值极易出现多解的现象。

本文在Mohr-Coulomb强度准则的假设下，利用最小二乘法的线性回归原理，通过MATLAB软件编制相应的计算程序，利用σ1-σ3回归方法进行抗剪强度的求解，为三轴试验求解抗剪强度指标提供了一条新思路。

1 数学模型

1.1 σ1-σ3法[8]

在对岩土体三轴试验数据进行分析时，假设岩土的剪切破坏强度满足M-C准则：

τ=σtanφ+C

(1)

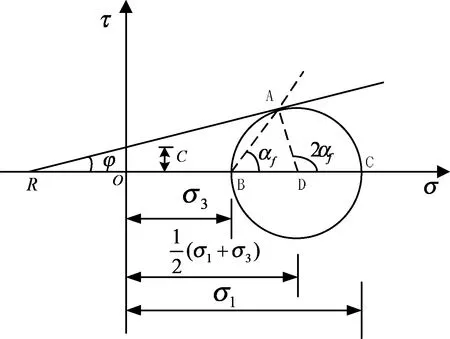
图1 极限平衡状态的应力圆

利用破坏应力圆知(见图1)：

(2)

整理后得

σ1=A+Bσ3

(3)

其中，

(4)

岩土三轴试验可以直接测得试样的大小主应力σ1i和σ3i，然后根据线性回归原理直接对(σ1i，σ3i)数据进行最小二乘法线性回归，得到A、B值，再利用式(4)通过反算就可以计算出抗剪强度c、φ值。

1.2 最小二乘法的一元线性回归

在工程实践和科学实验中，需要把实验数据拟合成经验公式，以反映变量之间的关系，这称为回归分析[9]。对于样本数据(xi，yi)，若存在yi=a+bxi+εi，并假定：

1) 误差εi是数学期望值为0、方差不变的随机变量，即E(εi)=0，Var(εi)不变；

2)xi为非随机变量。

则使

∑(yi-a-bxi)2=min

(5)

满足式(5)的a，b值是回归方程y=a+bx的回归系数的最佳线性无偏估计量。

a，b的值可以通过下式求得

(6)

2 MATLAB算法实现

MATLAB[10]软件的功能很强大，特别是在数值计算和可视化处理方面。它强大的内核中集成了海量的数值计算函数，而且覆盖面很全面，用户可以将所需解决的问题概化成数学表达式，计算结果就可以通过MATLAB强大的计算和可视化功能完美地展现出来。MATLAB具有函数和图形窗口两种进行曲线拟合的方法，考虑到本文拟合的强度包络线为线性函数，为了对不同的三轴试验数据进行多次重复计算应用，现采用第一种方法通过建立M函数对三轴试验数据进行拟合。

2.1 多项式拟合函数polyfit

在MATLAB中，进行多项式曲线拟合函数的调用格式为：

p=polyfit(x，y，n)

式中x，y采用矩阵形式，表示参与曲线拟合的实验数据；n为拟合多项式的次数，本文中为线性拟合，故n=1。

2.2 建立M函数

在MATLAB中，一个M函数就相当于一个独立的程序，本文在进行程序设计中，将最大主应力σ1和最小主应力σ3分别以矩阵的形式作为数据输入变量。只要按照一定的格式输入三轴压缩试验中的最大主应力和最小主应力的值，就可以得出抗剪强度指标c、φ的值，并可以显示强度包络线和莫尔应力圆的图形。

程序代码如下：

function moco (a3，a1) %a3为最小主应力，即围压，a1为最大主应力;

syms c fai;%定义粘聚力和内摩擦角

p=polyfit(a3，a1，1); %一次线性拟合

fai=(asin((p(1)-1)/(p(1)+1)))/pi*180; %求内摩擦角

c=p(2)*(1-sin(fai/180*pi))/(2*cos(fai/180*pi)); %求粘聚力

c=vpa(c，4) %控制计算精度

fai=vpa(fai，4) %控制计算精度

[m，n]=size(a3); %获取三轴试验组数

for i=1∶1∶n %画出所有的应力圆

alpha=0∶pi/50∶pi; %半圆角度[0，pi]

R=(a1(i)-a3(i))/2; %摩尔圆的半径

x=R*cos(alpha)+(a1(i)+a3(i))/2; %x的坐标

y=R*sin(alpha); %y的坐标

plot(x，y，‘-’) %画摩尔圆

hold on %多张图画在同一个坐标上

axis equal

end

x=0∶1∶1.2*a1(n);

y=x*tan(fai/180*pi)+c;

plot(x，y，‘r-’) %画强度包络线

xlabel(‘主应力σ/KPa’，‘fontsize’，14，‘fontname’，

‘Times new roman’);%x坐标控制

ylabel(‘剪应力τ/KPa’，‘fontsize’，14，‘fontname’，

‘Times new roman’);%y坐标控制

axis([0 1.2*a1(n) 0 0.7*a1(n)]); %坐标范围控制

title(‘应力圆和强度包络线’，‘fontsize’，14);%标题

axis on;axis xy;

3 算法验证与分析

为了验证MATLAB编程的正确性，本文参考选取了多组试验数据进行对比分析。算例1：参考文献[6]中的固结不排水剪切试验数据；算例2：参考文献[11]中的泥质粉砂岩三轴抗剪试验数据；算例3：参考文献[12]中的不固结不排水三轴剪切试验数据；算例4：参考文献[13]中砂岩的三轴试验数据。

根据不同参考文献提供的试验数据(即岩土体达到破坏状态下不同围压对应的极限轴向压应力)，参考文献中利用常规方法获得了每一组试验数据下的岩土体强度参数值，本文在此基础上利用笔者所编的程序进行重新计算，并与参考文献中得到的抗剪强度参数进行对比，见表1～4所示。

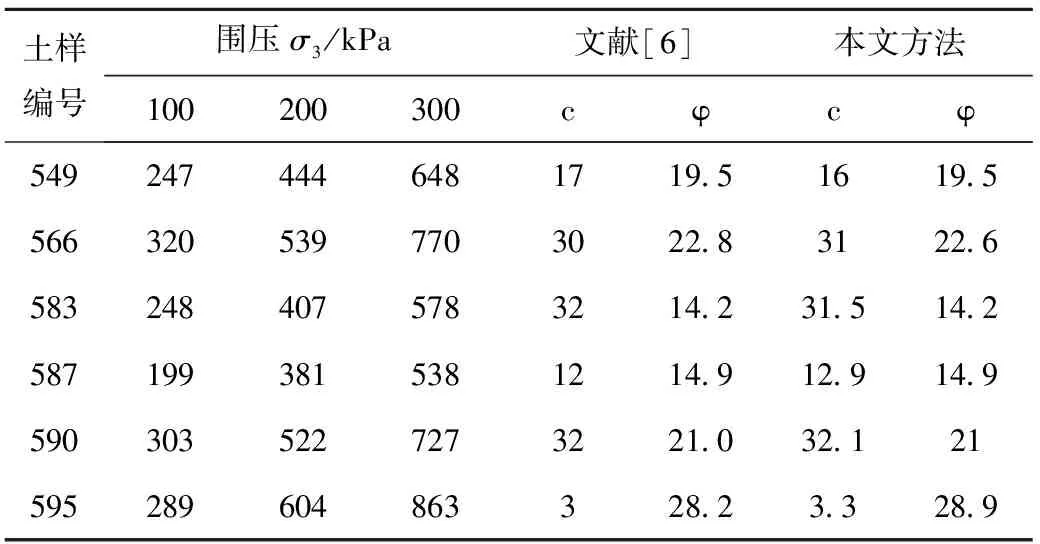
表1 某固结不排水剪切试验结果对比

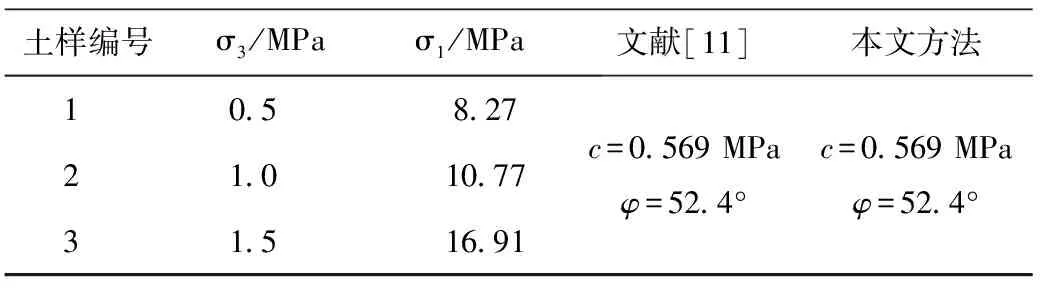
表2 某泥质粉砂岩剪切试验结果对比

表3 某土样不固结不排水剪切试验结果对比

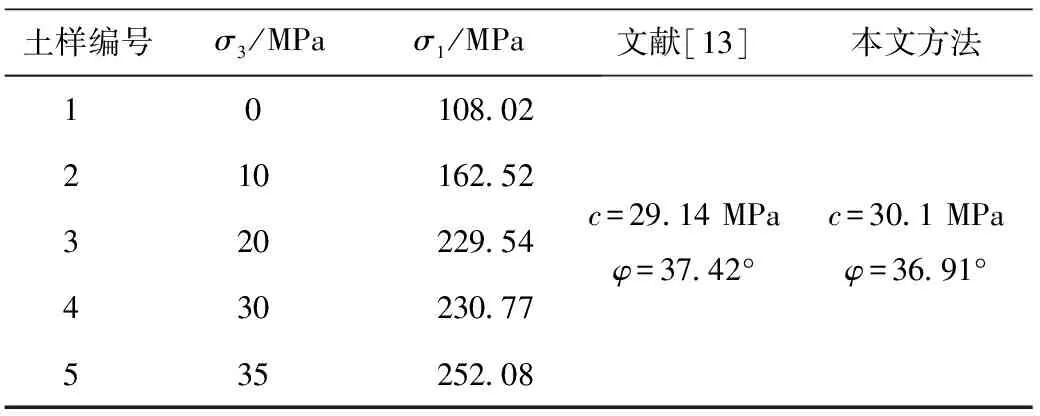
表4 某砂岩三轴剪切试验结果对比

从表1～4的数据中可以看出:各参考文献中提供的抗剪强度参数值与本文的计算值基本一致;φ值的整数部分基本完全一样，只是小数部分有些差异，c值差别相对大一些，这可能是由于直线的截距随着直线与横坐标夹角的微小变化而被放大的结果。不同参考文献对比结果的误差率详见表5。

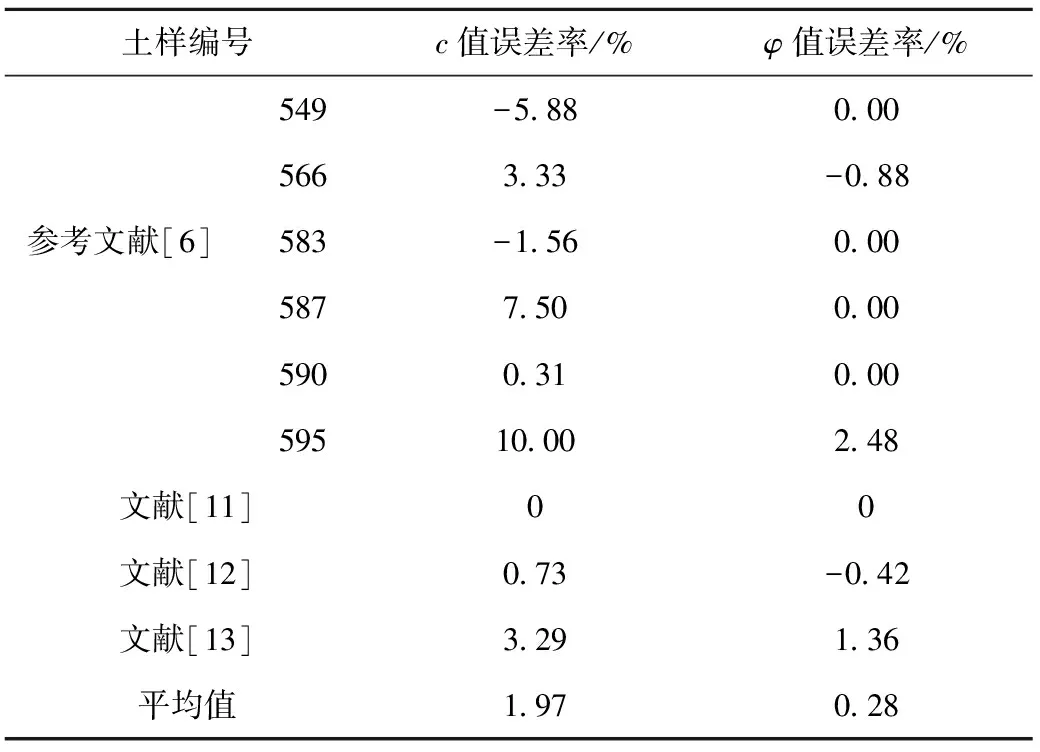
表5 本文计算值与参考文献结果的误差率

由表5可以看出：本文的计算方法与参考文献实验室结果的平均误差率c值为1.97%、φ值为0.28%，表明本文的方法是可靠的，而且本文的计算成果在精度上有了很大的提高，大大提高了数据处理效率，可以应用于工程实践中。

利用表1中编号583土样的数据可以绘制该土样的应力图及抗剪强度包络线，见图2。

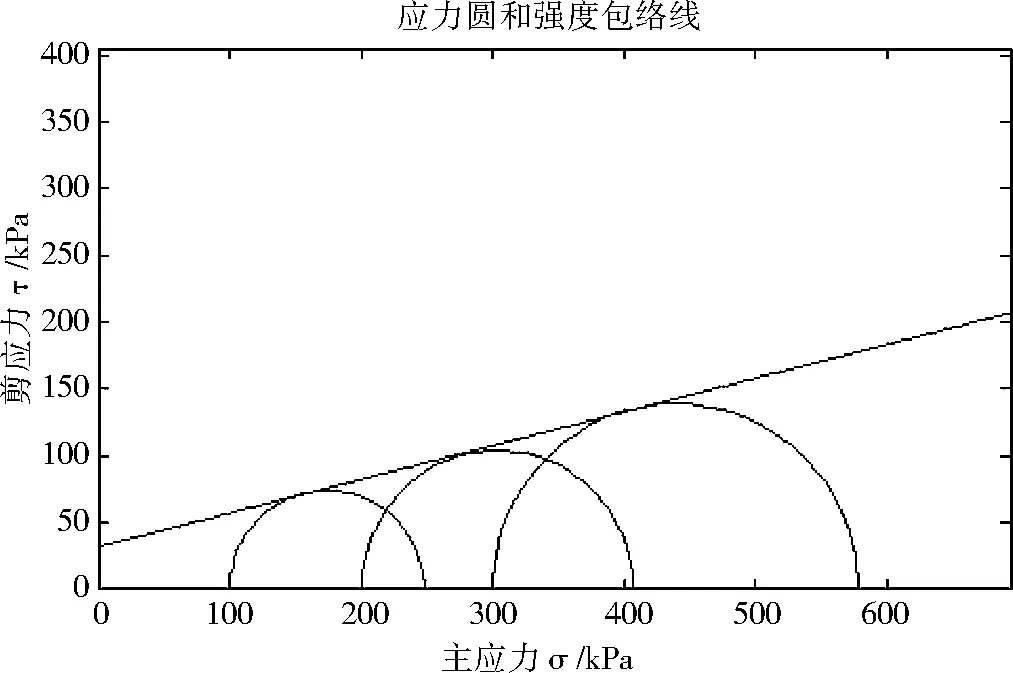
图2 应力圆和抗剪强度包络线

4 结语

本文利用MATLAB数值计算软件，基于岩土体的抗剪强度准则，编制相应的计算程序处理三轴试验数据，计算方法比较合理，精度和效率较高，计算结果比较合理且具有唯一性，较传统绘图方法优势比较明显，可供土工试验人员等参考。

[1] 孙敬.不同方法测定软土参数的比较分析[J]. 广东水利水电，2012(4)：20-22．

[2] 朱思军， 杨光华， 陈富强，等. 十字板剪切试验在珠三角深厚软土基坑工程中的应用[J]. 广东水利水电， 2016(6)：28-33．

[3] 南京水利科学研究院.土工试验规程：SL237—1999[S]. 北京:中国水利水电出版社，1999．

[4] 江稳琼. 浅谈固结、三轴试验中存在的一些问题及改进措施[J].广东水利水电，2009(5): 29-33．

[5] 阮波， 张向京， 彭意. Excel规划求解三轴试验抗剪强度指标[J]. 铁道科学与工程学报，2009，6(5)：57-60．

[6] 李小磊， 吴云刚.求解c、φ值的软件开发及试验验证[J]. 安全与环境工程，2010，17(1)：103-106．

[7] 王星辉. 三轴剪切总应力强度指标的回归求值[J]. 地球科学与环境学报，2004，26(1)：52-54．

[8] 陈立宏，陈祖煜，李广信.三轴试验抗剪强度指标线性回归方法的讨论[J]. 岩土力学，2005，26(11)：1 785-1 789．

[9] 郑咸义，姚仰新，雷秀仁，等，应用数值分析[M]. 广州：华南理工大学出版社，2008．

[10] 刘正君. MATLAB科学计算宝典[M]. 北京：电子工业出版社， 2012．

[11] 李雷， 陈尚星. 岩石三轴抗剪强度的计算[J].华北水利水电学院学报， 2002， 23(4):46-48．

[12] 张书宪， 刘春平. 求解三轴抗剪强度指标的一种方法[J]. 勘察科学技术， 1993(3):15-18．

[13] 杨同， 徐川. 岩土三轴试验中的粘聚力与内摩擦角[J]. 中国矿业， 2007， 16(12):104-107．

(本文责任编辑 马克俊)

The Solution Computation of Triaxial Tests Shear Strength Index Based On Matlab

MA Yong, WANG Fei, DU Xiuzhong

(Guangdong Research Institute of Water Resources and Hydropower, The Geotechnical EngineeringTechnology Center of Guangdong Province, Guangzhou 510635，China)

Mohr’s circle is widely used in soil mechanics; it is generally finite precision and affected by human factors due to be obtained by mapping method. This paper can obtain shear strength index of triaxial test by using Matlab software compiled corresponding program. The procedure can calculate the value of c、φ through the relation between the hear strength index and principal stress by using the principle of least square method. The accuracy and reliability of this method are verified by the relevant literature data, which provides a new way to calculate the shear strength of soil.

triaxial tests; shear strength index; matlab; least square method

2016-11-06;

2016-11-29

马勇(1988)，男，硕士，主要从事岩土工程设计咨询工作。

TU43

：B

：1008-0112(2016)012-0018-04