改进Pearson相关系数的个性化推荐算法

陈功平,王红

六安职业技术学院信息与电子工程学院,安徽六安237158

改进Pearson相关系数的个性化推荐算法

陈功平,王红

六安职业技术学院信息与电子工程学院,安徽六安237158

基于用户的协同过滤推荐算法(User CF)从用户的历史操作记录中分析用户的兴趣，找到每个用户的k个相似近邻，然后基于这k个近邻集合实施推荐。皮尔森相关系数能够根据用户的历史评分计算用户间的相似度。本文加入流行项目惩罚系数、共同评分项目惩罚系数δ和评分差异惩罚系数λ，对皮尔森相关系数实施了改进和修订。实验结果表明，改进后的皮尔森相似度的推荐效果好于原始皮尔森相似度。

个性化推荐;相似性计算;皮尔森相关系数;评分预测

个性化推荐[1]比大众化推荐更能满足当前用户的需要，如同静态网页为用户显示相同内容，动态网页为用户显示个性化的内容。个性化推荐[2]算法从用户的历史行为中研究用户兴趣，根据每个用户的喜好生成推荐列表。

协同过滤推荐（Collaborative Filtering，CF）算法[3]是推荐系统中应用广泛、研究深入又简单的推荐算法，有基于用户相似性的协同推荐算法（UserCF）[4]和基于项目相似性的协同推荐算法（ItemCF）[5]，UserCF从用户（User）对项目（Item）的评分矩阵中挖掘当前用户最相似的k个邻居，然后以k个邻居为基础实施推荐。本文采用改进的皮尔森相关系数计算用户间的相似度，降低共同评分项目过少、流行项目及评分差异三种因素对用户相似度的影响，改进相似度计算方法，提高评分预测的精度。实验结果表明，改进后的相似度计算方法的推荐效果好于原始相似度计算的推荐效果。

1 用户相似度评价指标

用户或项目的相似度计算是协同过滤推荐算法的核心[6]。计算用户u1与u2的相似度时，从评分矩阵中找出两个用户的共同评价项目集合，记作Vu1、Vu2，将向量集合Vu1与Vu2的相似度作为用户u1与u2的相似度。常用的相似度度量方法有Jaccard相关系数、余弦相似度和皮尔森相关系数。

1.1 Jaccard相关系数

Jaccard[7]相关系数用两个集合的并集和交集的比值来度量用户相似度，即。

从计算公式可以看出，Jaccard相关系数适用于计算离散型集合的相似度，若评分矩阵中各元素的值只用1（喜欢）、-1（不喜欢）和0（无关）表示，使用Jaccard相关系数计算用户相似度的效果较好。而对于非离散型的评分矩阵，因Jaccard相关系数没有考虑评分值对相似度的影响，因此对于5星或10级评分矩阵的相似度计算效果较差。

1.2 余弦相似度

余弦相似度[8]通过计算两个向量间的夹角余弦度值来衡量两个用户间的相似性，即。

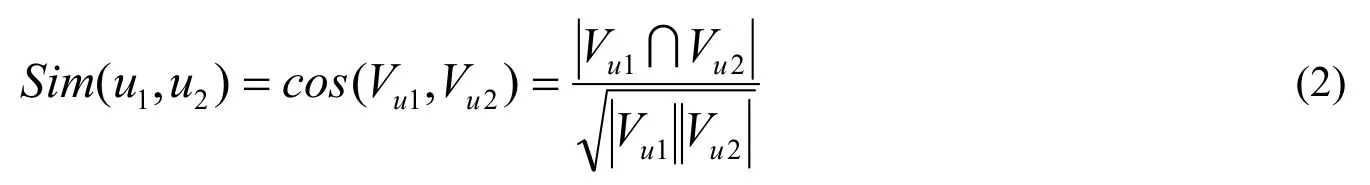
从公式可以看出，两个向量间的夹角越小则相似度越大，若夹角为0，认为u1和u2完全相似，即相似度值为1，这种计算方法忽视了向量间的距离。如图1中的u1、u2、u3，根据余弦相似度计算u1和u2的相似度为1，大于u1和u3的相似度，但在空间上，u1和u3的距离更接近。余弦相似度同样没有考虑评分矩阵中的评分值对相似度的影响。

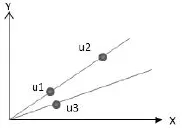
图1 余弦相似度示意图Fig.1 Sketch of cosine similarity

1.3 皮尔森相关系数

皮尔森相关系数[9]利用向量间的线性相关性表示用户相似度，即。

其中，ru1,i表示用户u1对项目i的评分，¯ru1表示用户u1对所有项目评分的平均值，皮尔森相似度的取值范围从[-1，1]，比Jaccard相关系数和余弦相似度的计算结果更精确[10]。

皮尔森相似度形式上和余弦相似度相似，计算时减去了用户的平均评价值，就是对余弦相似度做了一次归一化处理，统一了用户的评分标准。

2 皮尔森相关系数的改进

假如u1和u2用户共同评分项目较少且恰好满足公式（3）相似度为1的条件，这种情况在实际评分矩阵中非常常见，导致每个用户相似度为1的近邻的相同评价项目数较少，近邻计算结果与实际不符，因此需要改进原始皮尔森相似度的计算方式，加入限制条件。

2.1 热门项目惩罚

当某首歌曲流行时，几乎所有用户都会收听，所以热门项目对相似度计算的贡献较小[11]。这里将评分矩阵中评价数量作为项目热门的度量标准，为了降低热门项目对用户相似度的影响，将公式（3）修订为。

其中，N(i)表示项目i在评分矩阵中被评价的次数。

2.2 共项评分项目惩罚

为了降低偶尔相同评价对皮尔森相似度的影响，设置共同评价项目过少的惩罚阀值δ，将公式（4）改进为。

δ的取值太小则惩罚不明显，当取值达到一定限度时推荐效果趋于收敛。图2反应了δ值对推荐结果的影响，数据取自近邻数为100个、MovieLens 100 k数据集中测试集的评分预测的RMSE值变化，当δ在25以后趋于收敛。从图2可以看出，δ可以有效提高评分预测的准确度。

图2 δ对RMSE值的影响Fig.2 The influence of δ on RMSE value

2.3 共同评分差异性修正

皮尔森相似度已经对评分做了一次归一化处理，但如果u1和u2用户的平均分相似，而对某项目打分差值超过一定界限，认为这样的共同评分项对相似度贡献较小，加入共同评分差异性修正值λ。

r用来限制u1、u2对项目i评价差值的界限，∣ru1-ru2∣越小，即用户u1和u2对项目i的评分越接近，ε用于判定u1、u2平均分相似性的界限，修正值λ小于1，用于降低用户平均分相似而评分差值大对相似度的影响。

3 基于皮尔森相似度的个性化推荐算法

3.1 基于用户相似度的评分预测

用户会为喜爱的项目打高分，所以评分预测是推荐系统的实现原理之一。得到用户u的k个近邻后就可以预测u对项目i的评分，预测公式如（7）所示。

3.2 评价指标

使用均方根误差RMSE[12]作为算法的评价指标，RMSE反应的是预测分值与用户实际分值间的差异，值越小说明预测越准确[13]。

其中，rui表示用户u对项目i的实际评分，rˆui表示用户u对项目i的预测评分，∣T∣表示预测数量。

3.3 用户相似度训练

算法：改进Pearson相关系数的用户近邻计算

输入：训练集评分矩阵Train,k,δ,Max_δ,λ

输出：每个用户的k个最近邻矩阵Sim

1：RMSE[u1,u2,…]中各元素初始值为1

2：根据公式（3）计算用户间的皮尔森相似度并存入Sim

3：k个最近邻训练

3.1 根据公式（6）重新计算Sim

3.2 根据公式（7）预测Train中ui的评分

3.3 根据公式（8）计算RMSE[ui]值

3.4 δ++

3.5 直到RMSE[ui]<0.6或δ>=Max_δ

4 实验结果及分析

使用GroupLens发布的MovieLens 100 k数据集验证实验效果，该数据集[14]存储了10万条用户对电影的评分记录，每条记录由（用户编号，电影编号，评分值）3项组成，按照每个用户的评价数量，以8:2的比例随机分成训练集Train（80 k条记录）和测试集Test（20 k条记录），Movie Lens数据集初始情况如表1所示。

4.1 实验参数设置

本文通过4组实验验证改进皮尔森相似度对推荐结果准确度的影响，每组实验任务名及参数设置如表2所示。

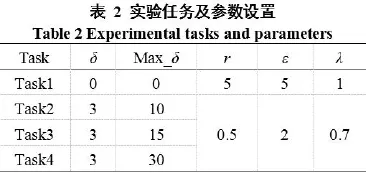
Task1的参数设置表示没有改进，相当于使用公式（3）为相似度计算方法，即原始皮尔森相似度系数，其余3组实验均对计算方法有所改进。

4.2 实验结果及分析

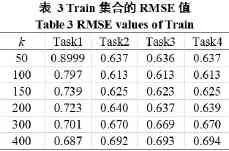
表3是Train集合的RMSE评价指标值。

从数据可见，在k值小于200的情况下，Task2～Task4明显比Task1效果好，在k为100时，Task2～Task4的预测效果最好；Task1随k值的增加效果越来越好，k值的增加会使得算法的时间复杂度升高；Task2～Task4在k值相同时RMSE值差值很小。

表4是Test集合的RMSE评价指标值。

在Test集合中，Task2～Task4的预测效果好于Task1，当k=100时，Task2和Task3的RMSE指标值比Task1的指标值提高了0.1。当k值升高，RMSE值降低，即k值越大，预测评分越接近实际评分。

图3是Train集合的RMSE指标值与k值的关系图，对于传统的皮尔森系数而言，k值越大预测越准确，而改进后的皮尔森相关系数的预测结果在k=100时出现拐点。

图4是Test集合的RMSE指标值与k值的关系图，与Train集合不同，二者都随着k值的升高而降低，改进相似度计算方法的测试效果好于传统计算方法。由图可以认为当k值超过一定限度后，改进相似度计算方法与传统相似度计算方法的预测结果的指标值越来越接近。

图3 Train集合的RMSE值比较Fig.3 Comparison of RMSE values in Train

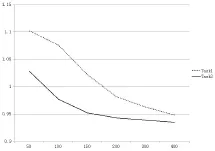
图4 Test集合的RMSE值比较Fig.3 Comparison of RMSE values in Test

5 总结

相似度计算方法是推荐算法的核心，皮尔森相关系数将用户评分数据参与到相似度计算过程，能够更准确的挖掘用户的兴趣，提高推荐效果。在实际应用时，由于用户数和项目数较大，相似度计算和推荐算法的时间复杂度过高，如果将相似度计算过程放在线下进行则不能实施实时推荐。降低相似度计算和推荐的时间复杂度、提供实时推荐是本文的下一个研究方向。

[1]ZhuangHL,TangJ,TangWB,etal.Activelylearningtoinfersocialties[J].DataMiningandKnowledgeDiscovery,2012,25(2):270-297

[2]高明,金澈清,钱卫宁,等.面向微博系统的实时个性化推荐[J].计算机学报,2014,37(4):363-375

[3]KaleliC.Anentropy-basedneighborselectionapproachforcollaborativefiltering[J].Knowledge-BasedSystems,2013,56(3):273-280

[4]吴湖,王永吉,王哲.两阶段联合聚类协同过滤算法[J].软件学报,2010,21(5):1042-1054

[5]黄创光,印鉴,汪静,等.不确定近邻的协同过滤推荐算法[J].计算机学报,2010,33(8):1369-1377

[6]刘树栋,孟祥武.基于位置的社会化网络推荐系统研究[J].计算机学报,2015,38(2):322-336

[7]Lu ML,Qin Z,Cao Y,et al.Scalable news recommendation using multi-dimensional similarity and Jaccard–Kmeans clustering[J].The Journal of Systems and Software,2014,95(4):242-251

[8]Aral S,Walker D.Identifying Influential and SusceptibleMembersof SocialNetworks[J].Science,2012,337(6092):337-341

[9]张宇镭,党琰,贺平安.利用Pearson相关系数定量分析生物亲缘关系[J].计算机工程与应用,2005(33):79-82,99

[10]Zhuang H,Savage EM.Variation and Pearson correlation coefficients of Warner-Bratzler shear force measurements within broiler breast fillets[J].Poultry Science,2009,88(1):214-20

[11]Jannach D,Zanker M,Felfemig A,et al.Recommender systems:an introduction[D].Cambridge:CUP,2010

[12]陈克寒,韩盼盼,吴健.基于用户聚类的异构社交网络推荐算法[J].计算机学报,2013,36(2):349-359

[13]朱郁筱,吕琳媛.推荐系统评价指标综述[J].电子科技大学学报,2012,41(2):163-175

[14]朱夏,宋爱波,东方,等.云计算环境下基于协同过滤的个性化推荐机制[J].计算机研究与发展,2014,51(10):2255-2269

APersonalized RecommendationAlgorithm on Improving Pearson Correlation Coefficient

CHEN Gong-ping,WANG Hong
College of Information and Electronic Engineering/Lu’an Vocation Technology College,Luan 237158,China

This paper found k similar neighbors of each user by analyzing the users’interests from their operating records based on the collaborative filtering recommendation and then made the implementation of recommendations based on the k similar neighbors.The Pearson Correlation Coefficient could calculate the similarity among users.This paper added popular items penalty coefficient,simultaneous rating items penalty coefficient δ and rating different penalty coefficient λ to the Pearson Correlation Coefficient and carried out the improvement and revised to the Pearson Correlation Coefficient.The experimental results indicated that the recommendation effect of improved Pearson Correlation Coefficient was better than the original one.

Personalized recommendation;similarity calculation;Pearson Correlation Coefficient;rating prediction

TP301

A

1000-2324(2016)06-0940-05

2015-03-31

2015-08-31

2015年度安徽高校自然科学研究重点项目(KJ2015A435);安徽省2016年高校优秀青年人才支持计划重点项目(gxyqZD2016570);安徽省2014年高校优秀青年人才支持计划

陈功平(1980-),男,讲师,研究方向:个性化推荐，计算机网络.E-mail:wh0115140@126.com

*通讯作者:Author for correspondence.E-mail:wh0115140@126.com