高校信息系统使用率聚类分析

谢日敏， 陈 杰， 游贵荣

(福建商业高等专科学校 a.信息管理工程系; b.信息网络中心, 福州 350012)

高校信息系统使用率聚类分析

谢日敏a， 陈 杰b， 游贵荣b

(福建商业高等专科学校 a.信息管理工程系; b.信息网络中心, 福州 350012)

针对高校信息化建设过程中教工对业务应用系统使用差异问题，建立教工聚类模型，促进业务推广.以高校信息系统使用率的数据为基础，利用K-Means算法聚类快速简单的优势，综合使用指标法、手肘法、直观法优化聚类个数，通过主成分分析和多维尺度分析对比实验，构建出教工信息化应用情况的聚类信息库，为高校推广信息系统及业务融合提供参考.

K-Means算法；聚类;信息系统

当前高校信息化建设实施过程更加注重信息多元化的发展，由于各业务部门建立了自身的业务平台，业务系统的多样性使得数据复杂度不断累积.因此，在构建数据中心的同时，需要实现高校教育数据的价值再发现[1-3].本文针对高校信息化实施过程中构建的高校教务系统、工资系统、图书系统、网络课程系统、科研管理系统、办公管理系统、邮件系统使用情况的数据为基础，利用K-Means聚类算法快速简单的优势，在优化聚类个数方面，综合使用指标法、手肘法、直观法3种评价方法，并利用主成分分析和多维尺度分析对教工信息系统的使用度进行聚类，进一步提升高校信息化管理能力和教学科研水平.

1 数据预处理

1.1 数据清理

数据清理主要由3部分构成:(1)扫描数据并寻找出差异性；(2)对残缺数据、错误数据及重复数据进行修正；(3)选择合适的数据转换[4].

高校在信息化建设过程中，通常会涉及到多个独立的业务系统，其应用情况存在多样性和复杂性等特点.本文选择某高校半年时段内关于业务系统使用情况的日志表，进行数据清理.信息系统使用情况日志表包括登录号、访问信息系统的URL地址、访问时间等属性，通过扫描数据，抽取出293名教工共18273条信息数据，并将文本表达的数据转换为数值表达，以便数据分析使用，如表1所示.

表1 业务系统使用次数

1.2 数据标准化处理

由于数据之间的量纲存在不一致性，往往影响数据分析的结果，故需要进行数据标准化处理，解决数据之间的可比性问题.数据转换的标准化方法有多种，主要包括：(1)最小-最大标准化；(2)Z-score标准化方法；(3)十进位标准化方法[5].

根据数据结构及业务的实际情况，依据最小-最大标准化方法，将原始数据进行线性变换，映射到[0-1]区间.

2 聚类过程分析与K值选择

K-Means是无监督学习的聚类算法，其算法的基本思路是在n维空间内的M个点集划分为K个聚类，使得类内的每个数据点与质心距离最小.K-Means作为一种简单快速的算法，在处理数据方面有绝对优势，并可以取得相对较好的效果[6].

K-Means算法影响的主要因素包括异常处理，数据降维，K值选择，初始质心的选择以及变量相关性等问题，其中K值的大小选择问题直接影响聚类的最终结果.在K-Means算法中，输入参数K值的确定，本身就是较难的问题.本文在研究K值选择问题上，综合以下三种方法相互比较，进行K值选择：

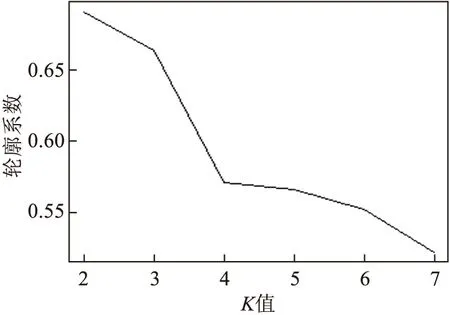
图1 轮廓系数与K值关系

2.1 聚类指标法

通过聚类指标来分析，包括邓恩指标、戴维斯指标、轮廓系数等方法[7-8].轮廓系数是图形显示的分区技术，通过比较内聚度和分离度，用其他类元素的平均距离对比在同一类内的平均距离，具有高轮廓值的元素表明是较好的聚类，低轮廓值的元素就有可能成为离群点.因此，轮廓系数与K-Means算法可以有效结合，来确定最优K值.

本文利用轮廓系数分析计算高校信息化系统应用情况，确定K值大小，如图1所示.

评估K时，由于评估对象是具有7个业务系统的数据维度，所以遍历K值为2到7.由于K-Means具有一定随机性，为避免局部最优问题，针对每一个K值，重复执行30次，并计算轮廓系数.如图1所示，当K取值为2时，有最大的轮廓系数值，表明具有较好的聚类效果.

轮廓系数法通过曲线的极值点对应的K值来确定聚类个数，虽然比较适合用来评估聚类算法的质量效果，但时间复杂度达到O(n2),时间代价高.

2.2 手肘法构造开销函数散点图

通过手肘法查看聚类效果，绘制出开销函数散点图，查看明显拐点处，即为最优K值.其中比较实用评估聚类数量的方法是GAP-statistic[9].其思想是设计出优化聚类方法的标准图，寻找出类似手肘的形态.常见方法是比较误差平方和(SSE)，计算类内的每个成员和类内的质心距离.简而言之，随着聚类的数量增加，误差平方和应该变小.因此，对连续聚类情况的误差平方和绘制图形，可以直观地判断出最优聚类情况.

具体的实现方法就是首先产生一组原始输入数据的随机值，然后计算出聚类的误差平方和.列数据生成的随机性，使得在随机矩阵中各个变量具有相同的平方差和标准差，如果数据集的鲁棒性较好，那么实际数据集误差平方和将比随机数据集误差平方和下降的更快.对应用类似因素分析的点状图进行分析，当误差平方和的变化放缓，即是最优选择的聚类方式.

如图2所示，呈现出数据集的手肘结构聚类情况.实际数据集要比生成的250个随机数据集的误差平方和下降速度更快.在K为2时聚类的误差平方和下降速度变缓.但是，这种手肘法的图形确定K值时，有时并不能显著识别.

因此，另一种评估方法是针对所测试聚类，检查实际数据集和随机数据集的误差平方和的绝对差异[10].实际数据集的误差平方和与随机数据集的误差平方和的均值具有不同情况，通过显示实际数据集的误差平方和与所有随机数据集的误差平方和均值，对比聚类情况.

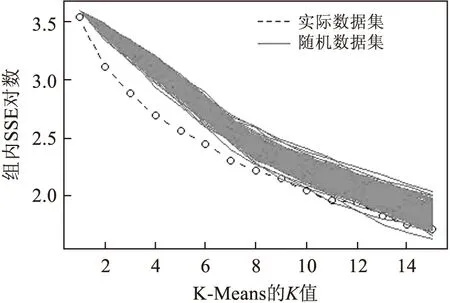
图2 误差平方和的聚类手肘法

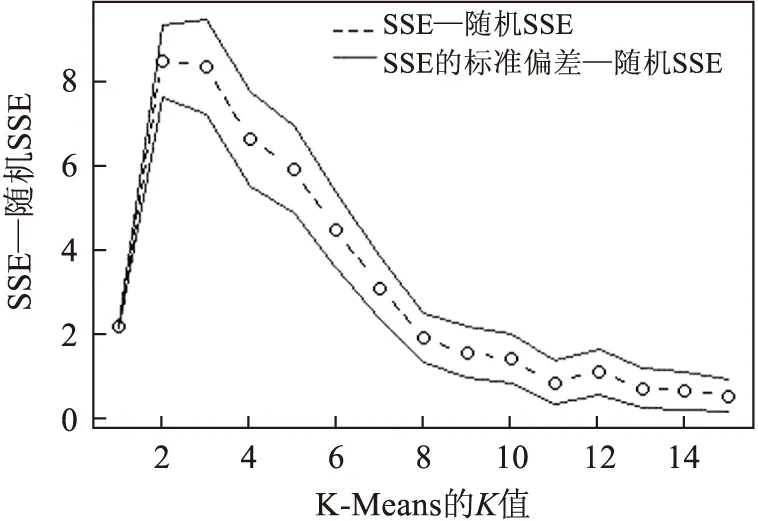
图3 SSE与随机SSE手肘法

如图3所示，实际数据集和随机数据集的误差平方和之间最大的转折发生在K为2的聚类.这表明K值为2是较为合理的选择.事实上，这是另一种手肘法计算最优K值.

手肘法比较直接易懂，但有时图形表达的手肘形态差异并不显著，不容易区分聚类个数.

2.3 直观图形法

完全依据评估参数选取K值而不考虑实际的应用场景是不适宜的，事实上如果各个数据维度都很明显地进行区分，在业务上能更直接地进行解释，即为聚类效果好.直观图形法可以利用密度分布和原始数据分布的箱线图等图形来直观判断数据分布情况.

如图4和图5，利用密度分布图和箱线图可以直观看出大部分教工半年业务系统的使用情况，故可将目标对象定性地分为低频和高频两类使用情况.

直观图形法对数据量较小情况能较快地进行数据图形化表达，其聚类情况主要依据对业务的熟悉程度，具有局部主观判断性.

3 实验与结果分析

为了检验聚类个数综合评价方法对K-Means算法的有效性，采用某高校教工使用信息系统半年的历史数据，依据聚类质量效果的3种评价方法相互佐证，确认K值为2，然后利用欧氏距离进行K-Means聚类分析.为了获得样本间的相似性空间表达，基于K-Means算法利用相关系数矩阵主成分分析(PCA)和多维尺度分析(MDS)相比较[11-12].如图6和图7所示，主成分分析的分布情况存在大量重叠区域，表明其鲁棒性不强，而采用多维尺度分析具有较好的数据分类结构.

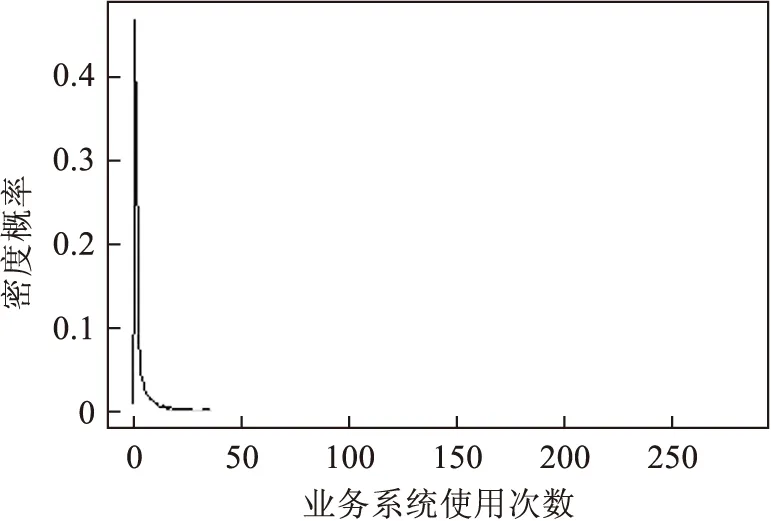
图4 密度分布

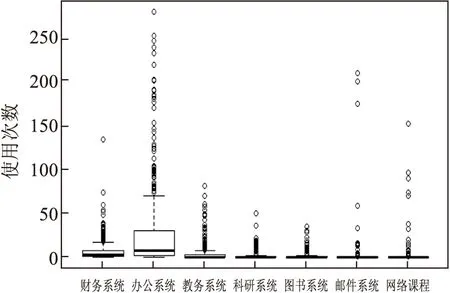
图5 原始数据分布箱线图

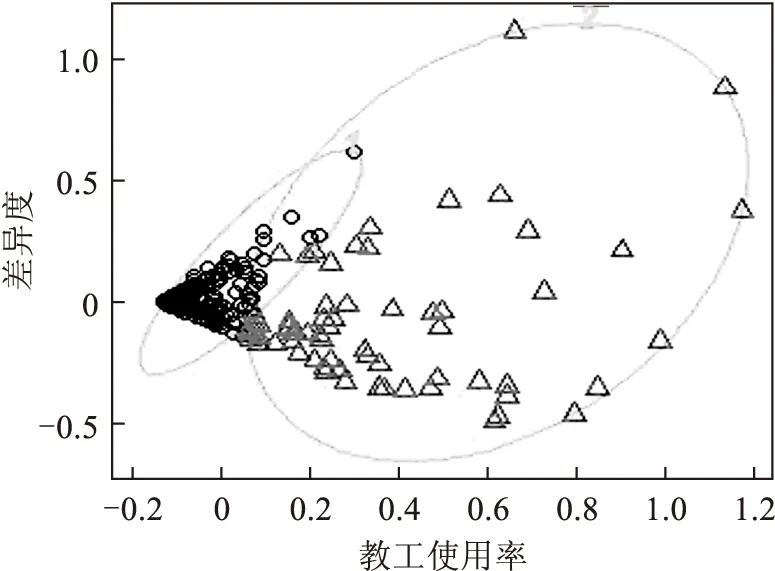
图6 主成分分析

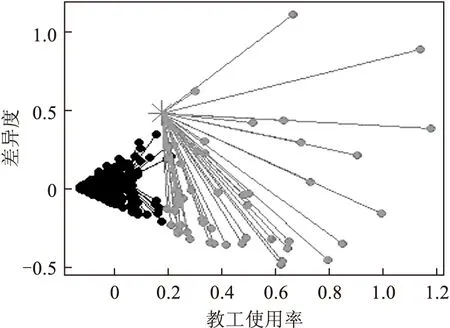
图7 多维尺度分析

对比主成分分析和多维尺度分析的K-Means聚类算法可以起到相辅相成作用，可以有效地分析高校信息系统教工使用情况.如图7所示，结合基于K-Means聚类分析结果的人员信息库，该校大部分人员的信息化应用情况属于第1类，其使用频度较低，而属于第2类的人员结构是信息化业务系统的一线工作人员和具有计算机专业背景的教师.通过对该校教工的工作岗位及高职院校职业能力分析，后期工作重点应对属于第1类中需要提升信息化业务水平的主要人员进行培训和深化学习，从而促进该校信息化发展[13].

本文确定K-means算法的K值选择，虽然数据来源于某高校的原始数据，数据结构分布相对容易区分，但是通过数据转换后，综合使用指标法、手肘法、直观法进行聚类个数的优化，依然能适应其他复杂的高校信息化聚类个数选择分析.

4 结语

通过综合使用指标法、手肘法、直观法相互佐证确定聚类个数，可以有效地分析高校信息化推进过程中所遇到的问题，从而构建出高校信息化聚类应用模型，促进高校从线下业务管理转变为线上业务管理，有利于弥补传统业务部门的缺失，提升了业务管理水平.

[1] MAYILVAGANAN M,KALPANADEVI D.Comparison of classification techniques for predicting the performance of students academic environment[C].IEEE,2014.

[2] THAKAR P,MEHTA A.Performance analysis and prediction in educational data mining:a research travelogue[J].International Journal of Computer Applications，2015,110(15):60-68.

[3] 陶丽娟.基于模糊数学聚类分析的高校教师绩效考核系统实现[J].计算机光盘软件与应用，2014(6):227-228.

[4] RAMAN V,HELLERSTEIN J M.Potter’s Wheel:An Interactive Data Cleaning System[C].VLDB，2001.

[5] HAN J,KAMBER M,PEI J.Data mining:concepts and techniques:concepts and techniques[M].Waltham,mA:Elsevier,2011:113-115.

[6] ARTHUR D,VASSILVITSKII S.k-means++:The advantages of careful seeding[C].Society for Industrial and Applied Mathematics,2007.

[7] ROUSSEEUW P J.Silhouettes:A graphical aid to the interpretation and validation of cluster analysis[J].Journal of Computational & Applied Mathematics,1987,20(4):53-65.

[8] LIU Y,LI Z,XIONG H,et al.Understanding of internal clustering validation measures[C].IEEE,2010.

[9] TIBSHIRANI R,WALTHER G,HASTIE T.Estimating the Number of Clusters in a Data Set via the Gap Statistic[J].Journal of the Royal Statistical Society,2000,63(2):411-423.

[10]KINTIGH K W,AMMERMAN A J.Heuristic Approaches to Spatial Analysis in Archaeology[J].American Antiquity,1982,47(1):31-63.

[11]PISON G,STRUYF A,ROUSSEEUW P J.Displaying a clustering with CLUSPLOT[J].Computational Statistics & Data Analysis,1999,30(4):381-392.

[12]BORG I,GROENEN P J.Modern multidimensional scaling:Theory and applications[M].New York:Springer Science & Business Media,2005:199-212.

[13]武来成，董新春.高职院校教师职业能力评价指标及模型的研究[J].中国林业教育，2015,33(1):30-34.

[责任编辑 马云彤]

Clustering Analysis of the Usage Rate of Information System in Colleges

XIE Ri-mina, CHEN Jieb, YOU Gui-rongb

(a. Department of Information Management and Engineering； b. Information Network Center,Fujian Commercial College, Fuzhou 350012, China)

In the process of the information construction in colleges, in order to solve the problem of differences in faculty’s usage of business application system, the clustering model was built for faculty and the business was promoted. In this paper, based on the data of the usage rate of the information system in colleges, by using of the advantages of fast and simple of the K-Means algorithm for clustering, the number of clusters was optimized by comprehensive using of the Elbow method, the index method and the intuitive method. The cluster database of faculty’s usage of the information technology was constructed by the principal component analysis, the multidimensional scaling analysis and the contrast experiment. All of above will provide a powerful reference for the promotion of information systems and the integration of business in colleges.

K-Means algorithm; clustering; information system

1008-5564(2016)05-0040-04

2016-05-16

2015年福建省青年教师科研项目，高校教育信息化专项“基于校园社交网络平台的应用系统架构研究”(JA15730)

谢日敏(1979—)，男，福建福州人，福建商业高等专科学校信息管理工程系讲师，硕士，主要从事数据挖掘研究.

TP391

A