半线性脉冲泛函微分方程正解的存在性

潘 欣 吴 正 王良龙

（安徽大学，安徽 合肥 230031）

半线性脉冲泛函微分方程正解的存在性

潘 欣 吴 正 王良龙

（安徽大学，安徽 合肥 230031）

本文利用线性算子半群理论，锥压缩不动点定理和Gronwall型脉冲积分不等式，在合适的条件下证明了抽象空间中半线性脉冲泛函微分方程正解的存在性。

紧C0-半群；半线性脉冲泛函微分方程；正解；Gronwall型脉冲积分不等式

引言

在生物数学和种群生物学等领域中，常常需要寻找微分方程的正解.因此，微分方程正解的存在性在实际问题中有很重要的应用。而许多数学物理方程可以转化为抽象空间中的微分方程。抽象空间中的微分方程也因此成为人们一直关注的课题。其中关于泛函微分方程获得了不少重要成果。见文[1，2，3]。

抽象空间中的半线性发展方程近来引起国内外学者广泛的研究兴趣，获得了不少重要结果，见文献[3－8]。其中文献[6－8]研究了半线性发展脉冲微分方程，受到以上文献的启发，本文考虑抽象空间上半线性脉冲泛函微分方程正解的存在性。

为此我们假设（E，|·|）为一个Banach空间，E＋为E上的一个正规锥（N为正规常数），E＋诱导E中的一个偏序关系≤（或≥），即对x，y∈E，x≤y当且仅当y－x∈E＋，则（E，|·|，≤）构成一个偏序Banach空间。文中E总是指偏序Banach空间。

以下考虑偏序Banach空间（E，|·|，≤）中半线性脉冲泛函微分方程Cauchy问题

正解的存在性。

1 预备知识

Cauchy问题（1）中的A为无界线性算子，可以生成一个正且紧的C0-半群 ｛T（ t）:t≥0｝；其中分别表示x（t）在t=tk处右极限，左极限；J=（0，+∞）；xt（θ）=x（t+θ），θ∈[-τ，0]（τ＞0）；τ1＞0.

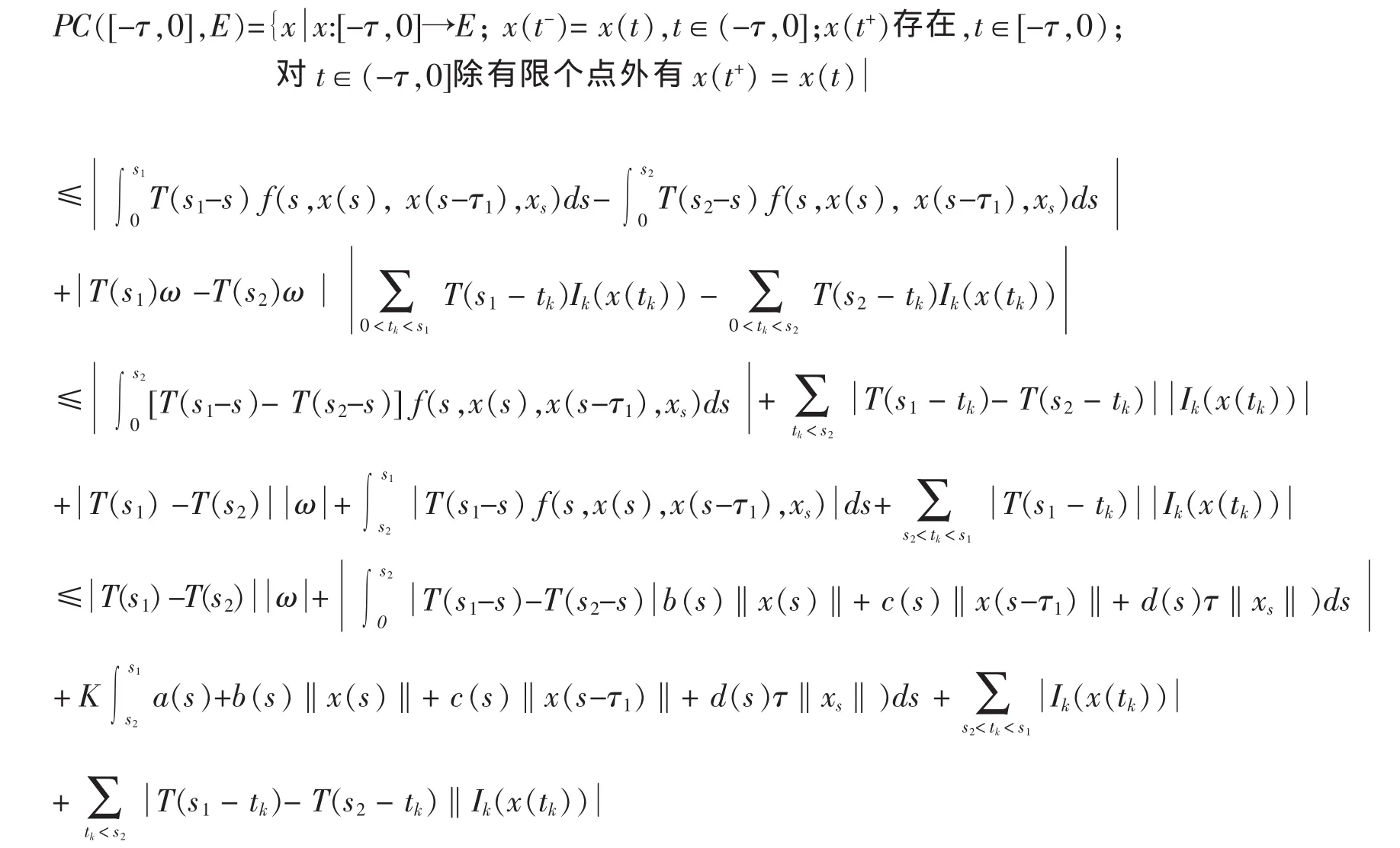
再由引理2可推知，对于任意的ε＞0，总可以找到一个δ＞0使得，其中x∈D且.所以（SD）（t）在（0，t1]上等度连续，类似地可以证明（SD）（t）在（0，T]上逐段等度连续，故SD是相对紧的。再由T的任意性知，算子S是PC+中的紧算子，从而是全连续算子，引理8得证。

主要定理 设PC+为PC[J，E]的一个正规锥且假设（H1），（H2）和（H3）均成立，则对于方程（1）在Banach空间PC[J，E]中至少存在一个全局正解

在给出主要结果之前，我们先证明几个重要的引理：

引理7 在假设（H1），（H2），（H3）的条件下，上述（3）式所定义的算子S∶PC+→PC+是连续的。

引理8 在假设（H1），（H2），（H3）的条件下，如（3）所定义的算子S是PC+中的紧算子，从而是全连续算子。

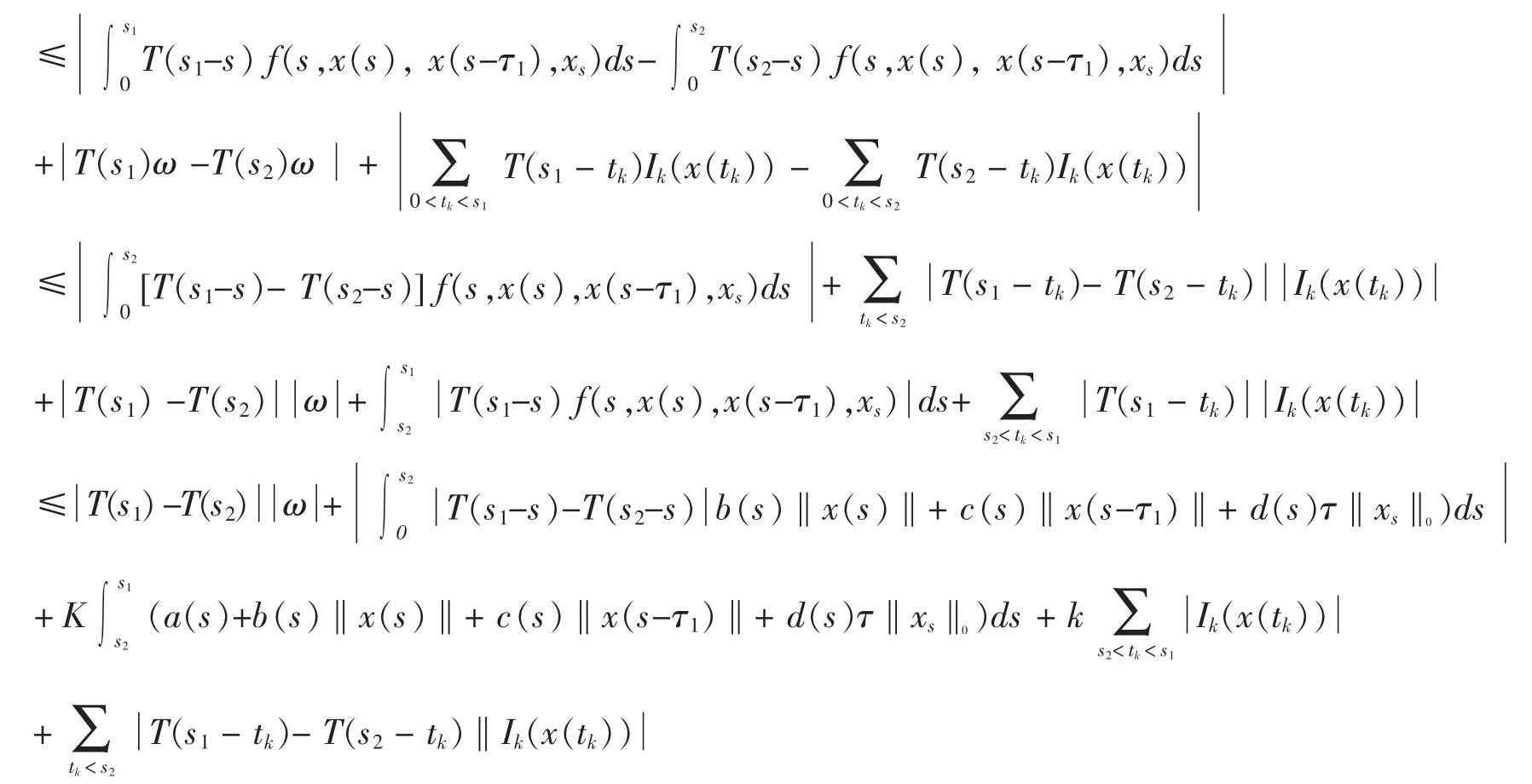
再由引理2可推知，对于任意的ε＞0，总可以找到一个δ＞0使得，其中x∈D且所以（SD）（t）在（0，t1]上等度连续，类似地可以证明（SD）（t）在（0，T]上逐段等度连续，故SD是相对紧的。再由T的任意性知，算子S是PC+中的紧算子，从而是全连续算子，引理8得证。

主要定理 设PC+为PC[J，E]的一个正规锥且假设（H1），（H2）和（H3）均成立，则对于ω∈E+｛0｝，方程（1）在Banach空间PC[J，E]中至少存在一个全局正解

3 应用举例

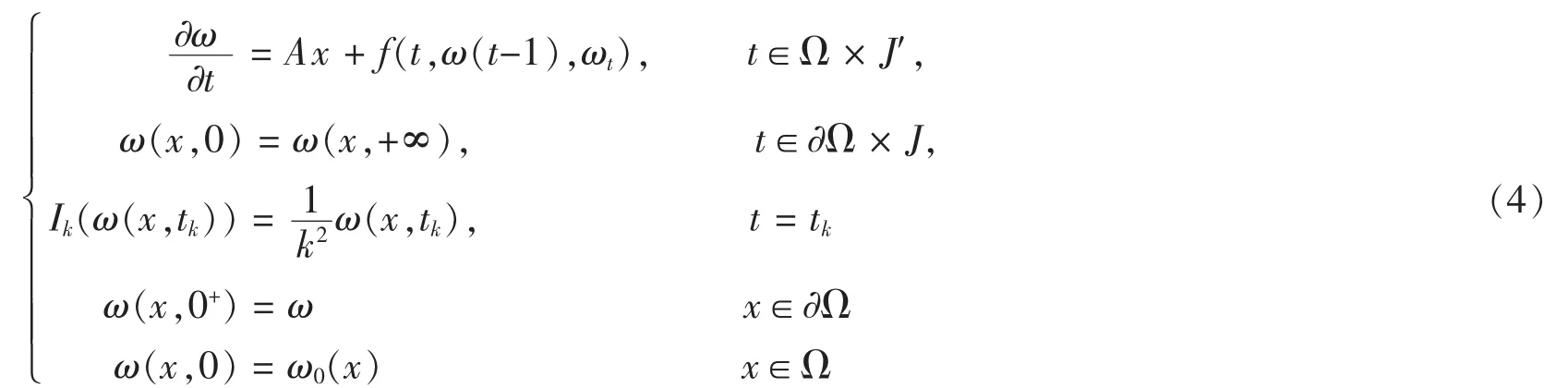
参考文献：

[1]郑祖庥.泛函微分方程理论[M].合肥：安徽教育出版社，1994.

[2]WU J H.Theory and applications of partial functional differential equations[M].Springer:New York.1996.

[3]王良龙.抽象半线性泛函微分方程正解的存在性[J].数学理论与应用，2001，（1）:94-99.

[4]WANG L L，WANG Z C.Monotone iterative techniques for parameterized BVPs of abstract semilinear evolution equations[J].Computers and Mathematics with Applications，2003，46（8-9）:1229-1243.

[5]WANG L L，WANG Z C.Mixed monotone iterative techniques for semilinear evolution equatons in banach spaces[J].Annals of Differential Equations，2004，（3）:283-301.

[6]潘欣，王良龙.半线性发展脉冲微分方程解的存在性[J].合肥学院学报（自然科学版），2009，（1）:5-8.

[7]潘欣，王良龙.半线性发展脉冲微分方程解的单调迭代方法[J].安庆师范学院学报（自然科学版），2014，（1）:15-19.

[8]潘欣，吴正.具有脉冲作用的半线性发展微分方程的正解[J].生物数学学报，2014，（3）:481-486.

[9]PAZY A.Semigroups of linear operators and applications to partial differential equations[M].Springer:New York.1983.

[10]宋新宇，郭红建，师向云.脉冲微分方程理论及其应用[M].北京：科学出版社，2011:26-27.

[11]郭大钧.非线性泛函分析[M].济南：山东科学技术出版社，2004:306.

THE EXISTENCE OF THE POSITIVE SOLUTIONS OF SEMILINEAR IMPULSIVE FUNCTIONAL DIFFERENTIAL EQUATIONS

PAN Xin WU ZhengWANG Liang-long
（Anhui University,Hefei Anhui 230031）

This paper is concerned with the existence of the positive solutions of semilinear impulsive functional differential equations in abstract space under the certain conditions by combining the semi-group theory of linear operators,the fixed point theorem in cones with the impulsive integral inequality of Gronwall type.

Compact-semigroup；Semilinear impulsive functional differential equations；Positive solutions；Impulsive integral inequality of Gronwall type

O175.15

A

1672－2868（2016）06－0005－06

责任编辑：杨松水 校对：陈 侃

2016－10－25

安徽省高校省级自然科学研究项目（项目编号：KJ2013Z012，KJ2014A010）；安徽省自然科学基金（项目编号：1508085QA01）；安徽省高等教育质量工程计划教学研究项目（编号：2015jyxm057）；安徽大学本科质量提升计划项目（项目编号：ZLTS2015052）

潘欣（1983-），男，安徽凤台人。安徽大学江淮学院，讲师。研究方向：微分方程与动力系统。